problemario-4-espectroscopia compress

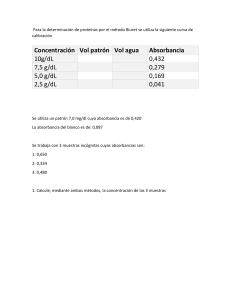
Elabora (n): García Nexticapan Ana
Hernández Inés José Armando
Rodríguez Rodríguez Jocelyn
NRC: 37450 Sección: 008
Matrícula: 201861039 Colegio: IAM
Matrícula: 201847528 Colegio: IQU
Matrícula: 201759255 Colegio: IAM
Unidad 3. MÉTODOS ESPECTROSCÓPICOS
Título del Contenido Temático: Espectroscopia
Problemario 4. Ejercicios de Espectroscopia.
1.
Calcular la Frecuencia en Hertz de:
a) Un haz de rayos X con longitud de onda de 2.65 Å.
𝑣=
𝑐
3𝑥108 𝑚/𝑠
= 1.1320𝑥 1018𝐻𝑧
=
𝜆 2.65x10−10𝑚
b) Una línea de emisión de cobre a 211.0 nm.
𝑣=
𝑐
3𝑥108 𝑚/𝑠
=
= 1.4218𝑥 1015𝐻𝑧
𝜆 211x10−9𝑚
c) La línea a 694.3 nm producida por un láser de rubí.
𝑣=
𝑐
3𝑥108 𝑚/𝑠
= 4.3208𝑥 1014 𝐻𝑧
=
𝜆 694.3x10−9𝑚
d) La salida de un láser de CO2 a 10.6 𝜇𝑚.
𝑣=
𝑐
3𝑥108 𝑚/𝑠
=
= 2.8301𝑥1013 𝐻𝑧
𝜆 10.6 x10−6 𝑚
𝑣=
𝑐
3𝑥108 𝑚/𝑠
= 1.5306𝑥1013 𝐻𝑧
=
𝜆 19.6 x10−6 𝑚
e) Una señal máxima de absorción infrarroja a 19.6 𝜇𝑚.
f)
Un haz de microondas a 1.86 cm.
𝑣=
𝑐 3𝑥1010𝑐𝑚/𝑠
= 1.6129𝑥1010𝐻𝑧
=
1.86 𝑐𝑚
𝜆
P á g i n a 1 | 19
2.
Calcular la longitud de onda en centímetros de:
a) Una torre de control de un aeropuerto que transmite a 118.6 MHz.
𝑐
3𝑥1010𝑐𝑚/𝑠
= 252.9510 𝑐𝑚
𝜆= =
𝑣 118 600 000 1⁄𝑠
b) Una radio para navegación que transmite a 114.10 KHz.
𝑐 3𝑥1010𝑐𝑚/𝑠
= 262 927.2568 𝑐𝑚
𝜆= =
𝑣 114 100 1⁄𝑠
c) Una señal de RMN a 105 MHz.
𝜆=
𝑐
3𝑥1010𝑐𝑚/𝑠
= 285.7142 𝑐𝑚
=
𝑣 105 000 000 1⁄𝑠
d) Una señal máxima de absorción en el infrarrojo con un número de onda de 1210 cm-1 (ṽ =
𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑜𝑛𝑑𝑎).
3.
𝜆=
1
1
= 8.2644𝑥 10−4 𝑐𝑚
=
ṽ 1210 1⁄𝑐𝑚
Un espectrofotómetro infrarrojo simple cubre un intervalo de longitud de onda de 3 a 15 𝜇𝑚.
Expresar este intervalo en:
a) Número de ondas
1
1
= 333 333.333 𝑚−1
=
𝜆 3x10−6m
1
1
= 66 666.666 𝑚−1
ṽ= =
𝜆 15x10−6m
𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑜 𝑑𝑒 333 333.333 1⁄ 𝑚 𝑎 66 666.666 1⁄𝑚
ṽ=
b) Hertz
𝑐 3𝑥108 𝑚/𝑠
= 1𝑥1014 𝐻𝑧
=
3x10−6m
𝜆
𝑐 3𝑥108 𝑚/𝑠
= 2𝑥1013 𝐻𝑧
𝑣= =
𝜆 15x10−6m
𝑣=
𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑜 𝑑𝑒 1𝑥 1014 𝐻𝑧 𝑎 2𝑥 1013 𝐻𝑧
P á g i n a 2 | 19
4.
Un sofisticado instrumento que detecta regiones de ultravioleta/visible/IR cercano tiene un
intervalo de longitud de onda de 185 a 3000 nm. ¿Cuáles son los intervalos del número de onda y
de la frecuencia?
a) Número de ondas
1
1
= 5 405 405.405 1⁄ 𝑚
=
𝜆 185x10−9m
1
1
= 333 333.333 1⁄ 𝑚
ṽ= =
𝜆 3000x10−9 m
𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑜 𝑑𝑒 5 405 405.405 1⁄ 𝑚 𝑎 333 333.333 1⁄ 𝑚
ṽ=
b) Hertz
𝑣=
3𝑥108 𝑚/𝑠
𝑐
=
= 1.6216𝑥 1015 𝐻𝑧
𝜆 185x10−9 m
𝑣=
𝑐
3𝑥108 𝑚/𝑠
=
= 1𝑥1014 𝐻𝑧
𝜆 3000x10−9m
𝐼𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑜 𝑑𝑒 1.6216𝑥 1015𝐻𝑧 𝑎 1𝑥1014 𝐻𝑧
5.
Calcular la frecuencia en Hertz y la energía en Joules de un fotón de rayos X con una longitud de
onda de 2.70 Å.
a)
Fórmula:
𝝀=
𝒗=
𝒄
2.70 Å |
10−8 𝑐𝑚
1Å
𝒗
𝒄
𝝀
| = 2.7 𝑥 10−8𝑐𝑚 = 𝜆
𝑐𝑚
𝑠 = 1.1111 𝑥 1018 1
𝑣=
2.7 𝑥 10−8 𝑐𝑚
𝑠
3 𝑥 1010
𝑣 = 1.1111 𝑥 1018 𝐻𝑧
P á g i n a 3 | 19
b)
Fórmula:
𝑬= 𝒉∙𝒗
Constante de Planck
𝐸 = (6.63 𝑥 10−34 𝐽 ∗ 𝑠) (1.1111 𝑥 1018 )
𝑠
1
𝐸 = 7.3665 𝑥 10−16 𝐽
6.
Calcular la longitud de onda y la energía en Joules asociadas a una señal de 220 MHz.
Fórmulas:
𝝀=
𝒄
𝒗
𝑬=𝒉∙𝒗
--- (Longitud de onda)
--- (Energía)
1
220 𝑀𝐻𝑧 = 220 𝑥 106 𝐻𝑧 = 220 𝑥 106
𝑠
𝑚
𝑠
𝝀=
1
220 𝑥 106
𝑠
Constante de Planck
3 𝑥 108
𝝀 = 1.3636 𝑚
1
𝐸 = (6.63 𝑥 10−34 𝐽 ∗ 𝑠) (220 𝑥 106 )
𝑠
𝐸 = 1.4586 𝑥 10−25 𝐽
7.
Calcular la longitud de onda de:
a) La línea de sodio a 589 nm en una solución acuosa que tiene un índice de refracción de 1.35.
𝜆=
𝜆0 589 𝑛𝑚
=
= 436.2962 𝑛𝑚
𝑛
1.35
b) Una señal de salida de un láser de rubí a 694.3 nm cuando pasa a través de un trozo de cuarzo
que tiene un índice de refracción de 1.55.
P á g i n a 4 | 19
𝜆=
8.
𝜆0
𝑛
=
694.3 𝑛𝑚 = 447.9354 𝑛𝑚
1.55
¿Cuáles son las unidades de absortividad (ε) cuando la trayectoria del rayo está dada en
centímetros y la concentración esta expresada en:
a) partes por millón?
𝜀=
𝐴
1
𝐿
=
=
𝑏𝑐 (𝑐𝑚)(𝑝𝑝𝑚) 𝑚𝑔 ∗ 𝑐𝑚
b) microgramos por litro?
𝜀=
𝐴
1
𝐿
=
=
𝜇𝑔
𝑏𝑐 (𝑐𝑚) ( ) 𝜇𝑔 ∗ 𝑐𝑚
𝐿
c) porcentaje en peso/volumen?
𝜀=
𝑚𝐿
𝐴
1
=
=
𝑏𝑐 (𝑐𝑚) (% 𝑃) 𝑔 ∗ 𝑐𝑚 ∗ 100 %
𝑉
d) gramos por litro?
𝜀=
𝐿
𝐴
1
=
=
𝑏𝑐 (𝑐𝑚) (𝑔) 𝑔 ∗ 𝑐𝑚
𝐿
P á g i n a 5 | 19
9.
Expresar las siguientes absorbancias en porcentaje de transmitancia:
𝑇=
A
%𝑇 = 10−𝐴 ∗ 100
T (%)
a) 0.0510
b) 0.918
c) 0.379
d) 0.261
e) 0.485
f) 0.702
10.
𝑃
𝑃0
𝑇 = 10−0.0510 = 0.8892 ∗ 100 = 88.92%
𝑇 = 10−0.918 = 0.1207 ∗ 100 = 12.07%
𝑇 = 10−0.379 = 0.4178 ∗ 100 = 41.78%
𝑇 = 10−0.261 = 0.5482 ∗ 100 = 54.82%
𝑇 = 10−0.485 = 0.3273 ∗ 100 = 32.73%
𝑇 = 10−0.702 = 0.1986 ∗ 100 = 19.86%
Convertir los siguientes datos de transmitancia en absorbancias:
𝐴 = − log ( 100)
%𝑇
T
a) 25.5%
b) 0.567
c) 32.8%
d) 3.58%
e) 0.085
f) 53.8%
𝐴 = − log (𝑇)
A
𝐴 = − log(0.255) = 0.5934
𝐴 = − log(0.567) = 0.2464
𝐴 = − log(0.328) = 0.4841
𝐴 = − log(0.0358) = 1.4461
𝐴 = − log(0.085) = 1.0705
𝐴 = − log(0.538) = 0.2692
P á g i n a 6 | 19
11.
Calcular el porcentaje de transmitancia de soluciones que tienen una absorbancia del doble
de las que tienen las soluciones del problema 9.
A
T (%)
a) 0.102
b) 1.836
c) 0.758
d) 0.522
e) 0.97
f) 1.404
12.
𝑇 = 10−0.102 = 0.7906 ∗ 100 = 79.06%
𝑇 = 10−1.836 = 0.0145 ∗ 100 = 1.45%
𝑇 = 10−0.758 = 0.1745 ∗ 100 = 17.45%
𝑇 = 10−0.522 = 0.3006 ∗ 100 = 30.06%
𝑇 = 10−0.97 = 0.1071 ∗ 100 = 10.71%
𝑇 = 10−1.404 = 0.0394 ∗ 100 = 3.94%
Calcular las absorbancias de soluciones que tienen una transmitancia de la mitad de las que
tienen las soluciones en el problema 10.
T
a) 12.75%
b) 0.2835
c) 16.4%
d) 1.79%
e) 0.0425
f) 26.9%
A
𝐴 = − log(0.1275) = 0.8944
𝐴 = − log(0.2835) = 0.5474
𝐴 = − log(0.164) = 0.7851
𝐴 = − log(0.0179) = 1.7471
𝐴 = − log(0.0425) = 1.3716
𝐴 = − log(0.269) = 0.5702
P á g i n a 7 | 19
13.
Completar las cantidades que faltan en la tabla. Cuando sea necesario, usar un valor de 200
para la masa del analito.
ε
A
0.172
0.3477
0.520
0.4023
0.6378
0.0777
0.798
0.9546
1.2814
0.179
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
%T
67.2976
44.9
30.1995
39.6
23.0250
83.6
15.9220
11.1
5.23
66.2216
a) %𝑇 = 10−𝐴 ∗ 100
𝜶
Lmol-1cm-1 cm-1ppm-1
𝟒. 𝟐𝟑𝒙𝟏𝟎𝟑
0.0211
5160.3998
0.0258
𝟕. 𝟗𝟓𝒙𝟏𝟎𝟑
0.0397
18240.3978
0.0912
𝟑
0.0186
𝟑. 𝟕𝟑𝒙𝟏𝟎
9628.2527
0.0481
3166.6666
0.0158
𝟒
0.0675
𝟏. 𝟑𝟓𝒙𝟏𝟎
𝟑
0.0489
𝟗. 𝟕𝟖𝒙𝟏𝟎
2489.5688
0.0124
b
cm
1.00
0.4991
1.00
2.5063
0.10
1.00
1.50
1.0001
5.0008
1.00
c
M
4.0661𝑥 10−5
𝟏. 𝟑𝟓𝒙𝟏𝟎−𝟒
6.5408 𝑥10−5
8.8 𝑥10−6
𝟏. 𝟕𝟏 𝒙𝟏𝟎−𝟑
𝟖. 𝟎𝟕 𝒙𝟏𝟎−𝟔
1.68𝑥10−4
𝟕. 𝟎𝟕 𝒙𝟏𝟎−𝟓
2.62𝑥10−5
𝟕. 𝟏𝟗 𝒙𝟏𝟎−𝟓
ppm
8.1322
27
13.0816
1.76
342
1.614
33.6
14.14
5.24
14.38
%𝑇 = 10−0.172 ∗ 100 = 67.2976 % 𝑑𝑒 𝑇𝑟𝑎𝑛𝑠𝑚𝑖𝑡𝑎𝑛𝑐𝑖𝑎
𝑐=
𝐴
=
𝜀𝑏
0.172
𝑚𝑜𝑙
= 4.0661𝑥10−5
𝐿
𝐿
(4.23𝑥103 𝑚𝑜𝑙 ∗ 𝑐𝑚) (1 𝑐𝑚)
𝑐 = 4.0661𝑥10−5
𝛼=
𝐴
0.172
= 0.0211 𝑐𝑚−1 𝑝𝑝𝑚−1
=
𝑏𝑐 (1 𝑐𝑚)(8.1322 𝑝𝑝𝑚)
b) 𝐴 = − log (
𝐴 = − log (
%𝑇
100
)
44.9
) = 0.3477 𝑑𝑒 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎
100
𝑐 = 1.35𝑥10
𝑏=
𝑚𝑜𝑙
𝑔
𝑔 1000 𝑚𝑔
𝑚𝑔 1𝑝𝑝𝑚
(200
| = 8.1322
| = 8.1322 𝑝𝑝𝑚
) = 8.1322 𝑥10−3
|
|
𝐿
1𝑔
𝐿
𝑚𝑜𝑙
𝐿 1 𝑚𝑔
𝐿
−4 𝑚𝑜𝑙
𝐿
(200
𝑔
𝑔 1000 𝑚𝑔
𝑚𝑔 1𝑝𝑝𝑚
| = 27
| = 27 𝑝𝑝𝑚
) = 0.027 |
|
1𝑔
𝑚𝑜𝑙
𝐿
𝐿 1 𝑚𝑔
𝐿
𝐴
0.3477
0.3477
=
=
= 0.4991 𝑐𝑚
0.6966
0.0258
𝑎𝑐
(27
𝑝𝑝𝑚)
𝑐𝑚 ∗ 𝑝𝑝𝑚
𝑐𝑚
P á g i n a 8 | 19
𝐴
=
𝑏𝑐
𝜀=
0.3477
( 0.4991 𝑐𝑚) (1.35𝑥10
c) %𝑇 = 10−𝐴 ∗ 100
−4
𝑚𝑜𝑙
𝐿 )
= 5160.3998 𝐿𝑚𝑜𝑙−1 𝑐𝑚−1
%𝑇 = 10−0.520 ∗ 100 = 30.1995 % 𝑑𝑒 𝑇𝑟𝑎𝑛𝑠𝑚𝑖𝑡𝑎𝑛𝑐𝑖𝑎
𝑐=
𝐴
0.520
𝑚𝑜𝑙
= 6.5408 𝑥10−5
=
𝐿
𝐿
𝜀𝑏 (7.95𝑥103
(1
𝑚𝑜𝑙 ∗ 𝑐𝑚) 𝑐𝑚)
𝑐 = 6.5408 𝑥10−5
𝛼=
𝑚𝑜𝑙
𝑔
𝑔 1000 𝑚𝑔
𝑚𝑔 1𝑝𝑝𝑚
(200
| = 13.0816
| = 13.0816 𝑝𝑝𝑚
) = 0.0130816 |
|
𝐿
1𝑔
𝑚𝑜𝑙
𝐿
𝐿 1 𝑚𝑔
𝐿
𝐴
0.520
=
= 0.0397 𝑐𝑚−1 𝑝𝑝𝑚−1
𝑏𝑐 (1 𝑐𝑚)(13.0816 𝑝𝑝𝑚)
d) 𝐴 = − log ( 100)
%𝑇
39.6
) = 0.4023 𝑑𝑒 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎
100
0.4023
0.4023
𝐴
=
=
= 2.5063 𝑐𝑚
𝑏=
0.0912
0.160512
𝑎𝑐
(1.76
𝑝𝑝𝑚)
𝑐𝑚 ∗ 𝑝𝑝𝑚
𝑐𝑚
𝐴 = − log (
𝑐 = 1.76 𝑝𝑝𝑚 = 1.76
𝑚𝑔
1𝑔
𝑔
| = 1.76𝑥10−3
|
𝐿 1000 𝑚𝑔
𝐿
𝑔
1.76𝑥10−3
𝐿 = 8.8𝑥10−6 𝑚𝑜𝑙
𝑐=
𝑔
𝐿
200 𝑚𝑜𝑙
𝐴
0.4023
= 18240.3978 𝐿𝑚𝑜𝑙−1 𝑐𝑚−1
𝜀= =
𝑏𝑐 ( 2.5063 𝑐𝑚) (8.8𝑥10−6 𝑚𝑜𝑙 )
𝐿
e) 𝐴 = 𝜀𝑏𝑐
𝐴 = (3.73𝑥10
3
𝐿
−3 𝑚𝑜𝑙
) (0.10 𝑐𝑚) (1.71 𝑥10
) = 0.6378 𝑑𝑒 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎
𝑚𝑜𝑙 ∗ 𝑐𝑚
𝐿
%𝑇 = 10−𝐴 ∗ 100
%𝑇 = 10−0.6378 ∗ 100 = 23.0250 % 𝑑𝑒 𝑇𝑟𝑎𝑛𝑠𝑚𝑖𝑡𝑎𝑛𝑐𝑖𝑎
𝑐 = 1.71 𝑥10
−3 𝑚𝑜𝑙
𝐿
(200
𝑔
𝑔 1000 𝑚𝑔
𝑚𝑔 1𝑝𝑝𝑚
| = 342
| = 342 𝑝𝑝𝑚
) = 0.342 |
|
1𝑔
𝑚𝑜𝑙
𝐿
𝐿 1 𝑚𝑔
𝐿
P á g i n a 9 | 19
𝛼=
𝐴
𝑏𝑐
0.6378
= 0.0186 𝑐𝑚−1 𝑝𝑝𝑚−1
= (0.10 𝑐𝑚)(342 𝑝𝑝𝑚)
f) 𝐴 = − log (
%𝑇
100
)
83.6
) = 0.0777 𝑑𝑒 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎
100
𝐴
0.0777
𝜀= =
= 9628.2527 𝐿𝑚𝑜𝑙−1 𝑐𝑚−1
𝑏𝑐
−6 𝑚𝑜𝑙
( 1 𝑐𝑚) (8.07 𝑥10
)
𝐴 = − log (
𝑐 = 8.07
𝛼=
𝑥10−6
𝐿
𝑚𝑔 1𝑝𝑝𝑚
𝑚𝑜𝑙
𝑔
−3 𝑔 1000 𝑚𝑔
) = 1.614 𝑥10
| = 1.614
|
| = 1.614 𝑝𝑝𝑚
(200
|
𝑚𝑜𝑙
1𝑔
𝐿 1 𝑚𝑔
𝐿
𝐿
𝐿
𝐴
0.0777
=
= 0.0481 𝑐𝑚−1 𝑝𝑝𝑚−1
𝑏𝑐 (1 𝑐𝑚)(1.614 𝑝𝑝𝑚)
g) %𝑇 = 10−𝐴 ∗ 100
%𝑇 = 10−0.798 ∗ 100 = 15.9220 % 𝑑𝑒 𝑇𝑟𝑎𝑛𝑠𝑚𝑖𝑡𝑎𝑛𝑐𝑖𝑎
𝛼=
0.798
𝐴
=
= 0.0158 𝑐𝑚−1 𝑝𝑝𝑚−1
𝑏𝑐 (1.50 𝑐𝑚)(33.6 𝑝𝑝𝑚)
𝑐 = 33.6 𝑝𝑝𝑚 = 33.6
1𝑔
𝑔
𝑚𝑔
| = 0.0336
|
𝐿 1000 𝑚𝑔
𝐿
𝑔
0.0336 𝐿
𝑚𝑜𝑙
−4
𝑐=
𝑔 = 1.68𝑥10
𝐿
200
𝑚𝑜𝑙
𝐴
0.798
= 3166.6666 𝐿𝑚𝑜𝑙−1 𝑐𝑚−1
𝜀= =
𝑚𝑜𝑙
𝑏𝑐 (
−4
1.50 𝑐𝑚) (1.68𝑥10
𝐿 )
%𝑇
h) 𝐴 = − log ( 100)
𝐴 = − log (
𝑐 = 7.07
𝐴
𝑏=
=
𝜀𝑐
𝛼=
11.1
100
) = 0.9546 𝑑𝑒 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎
𝑥10−5
𝑔 1000 𝑚𝑔
𝑚𝑔 1𝑝𝑝𝑚
𝑚𝑜𝑙
𝑔
| = 14.14
| = 14.14 𝑝𝑝𝑚
(200
) = 0.01414 |
|
1𝑔
𝐿
𝑚𝑜𝑙
𝐿 1 𝑚𝑔
𝐿
𝐿
0.9546
1.35𝑥104 𝑚𝑜𝑙 ∗ 𝑐𝑚 (7.07 𝑥10−5
𝑚𝑜𝑙
𝐿 )
= 1.0001 𝑐𝑚
𝐴
0.9546
=
= 0.0675 𝑐𝑚−1 𝑝𝑝𝑚−1
𝑏𝑐 (1.0001 𝑐𝑚)(14.14 𝑝𝑝𝑚)
𝐿
P á g i n a 10 | 19
%𝑇
i) 𝐴 = − log ( 100)
𝐴 = − log (
5.23
100
) = 1.2814 𝑑𝑒 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎
𝑐 = 5.24 𝑝𝑝𝑚 = 5.24
𝑚𝑔
1𝑔
−3 𝑔
| = 5.24𝑥10
|
𝐿 1000 𝑚𝑔
𝐿
𝑔
5.24𝑥10−3
𝐿 = 2.62𝑥10−5 𝑚𝑜𝑙
𝑐=
𝑔
𝐿
200 𝑚𝑜𝑙
𝐴
1.2814
= 5.0008 𝑐𝑚
𝑏=
=
𝐿
𝑚𝑜𝑙
3
𝜀𝑐
−5
9.78𝑥10 𝑚𝑜𝑙 ∗ 𝑐𝑚 (2.62𝑥10
𝐿 )
𝛼=
𝐴
1.2814
= 0.0489 𝑐𝑚−1 𝑝𝑝𝑚−1
=
𝑏𝑐 (5.0008 𝑐𝑚)(5.24 𝑝𝑝𝑚)
j) %𝑇 = 10−𝐴 ∗ 100
%𝑇 = 10−0.179 ∗ 100 = 66.2216 % 𝑑𝑒 𝑇𝑟𝑎𝑛𝑠𝑚𝑖𝑡𝑎𝑛𝑐𝑖𝑎
𝑐 = 7.19 𝑥10
𝛼=
𝜀=
−5
𝑔 1000 𝑚𝑔
𝑚𝑔 1𝑝𝑝𝑚
𝑚𝑜𝑙
𝑔
| = 14.38
| = 14.38 𝑝𝑝𝑚
(200
) = 0.01438 |
|
1𝑔
𝐿
𝑚𝑜𝑙
𝐿 1 𝑚𝑔
𝐿
𝐿
0.179
𝐴
=
= 0.0124 𝑐𝑚−1 𝑝𝑝𝑚−1
𝑏𝑐 (1 𝑐𝑚)(14.38 𝑝𝑝𝑚)
𝐴
=
𝑏𝑐 (
14.
0.179
1 𝑐𝑚) (7.19 𝑥10−5
𝑚𝑜𝑙
𝐿 )
= 2489.5688 𝐿𝑚𝑜𝑙−1 𝑐𝑚−1
Una solución que contiene 4.48 ppm de KMnO4 tiene una transmitancia de 0.309 en una
celda de 1 cm a 520 nm. Calcular la absortividad molar del KMnO4.
Datos:
𝑐 = 4.48 𝑝𝑝𝑚
𝑇 = 0.309
𝑏 = 1 𝑐𝑚
𝑃𝑀 = 158.034
𝑔
𝑚𝑜𝑙
P á g i n a 11 | 19
𝑐 = 4.48 𝑝𝑝𝑚 = 4.48
𝑚𝑔
1𝑔
𝑔
|
| = 4.48𝑥 10−3 𝐿
𝐿 1000 𝑚𝑔
𝑔
4.48𝑥 10−3 𝐿
𝑚𝑜𝑙
−5
𝑐=
𝑔 = 2.8348 𝑥 10
𝐿
158.034 𝑚𝑜𝑙
𝜀=
15.
𝐴 = − log (0.309) = 0.51 𝑑𝑒 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎
𝐴
0.51
=
= 17990.6871 𝐿𝑚𝑜𝑙−1 𝑐𝑚−1
𝑚𝑜𝑙
𝑏𝑐 (
1 𝑐𝑚) (2.8348 𝑥10−5 𝐿 )
El berilio (II) forma un complejo con acetil-acetona (166.2 g/mol). Calcular la absortividad
molar del complejo, dado que una solución de 1.34 ppm tiene una transmitancia de 55.7% cuando
se mide en una celda de 1 cm a 295 nm, la longitud de onda para la absorción máxima.
Datos:
𝑐 = 1.34 𝑝𝑝𝑚
𝑇 = 55.7 %
𝑏 = 1 𝑐𝑚
𝑃𝑀 = 166.2
𝑔
𝑚𝑜𝑙
𝑚𝑔
1𝑔
𝑔
|
| = 1.34𝑥 10−3
𝐿
𝐿 1000 𝑚𝑔
𝑔
1.34𝑥 10−3
𝑚𝑜𝑙
𝐿
−6
𝑐=
𝑔 = 8.0625 𝑥 10
𝐿
166.2 𝑚𝑜𝑙
55.7
𝐴 = − log (
) = 0.2541 𝑑𝑒 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎
100
𝐴
0.2541
𝜀= =
= 31516.279 𝐿𝑚𝑜𝑙−1 𝑐𝑚−1
𝑚𝑜𝑙
𝑏𝑐 (
−6
1 𝑐𝑚) (8.0625 𝑥10 𝐿 )
𝑐 = 1.34 𝑝𝑝𝑚 = 1.34
P á g i n a 12 | 19
16.
A 580 nm, la longitud de onda de su máxima absorción, el complejo de Fe (SCN)2+ tiene una
absortividad molar de 7.00 x 103 L mol-1cm-1. Calcular
a) La absorbancia de una solución 2.50x10-5 M del complejo a 580 nm en una celda de 1.00 cm.
𝐴 = 𝜀 ∗ 𝑙 ∗ 𝑐 = (7𝑥 103
𝐿
𝑚𝑜𝑙
) (1 𝑐𝑚) (2.5x10−5
) = 0.175
𝐿
𝑚𝑜𝑙 ∗ 𝑐𝑚
b) La absorbancia de una solución en la que el complejo tiene una concentración del doble que
en a).
𝐴 = 𝜀 ∗ 𝑙 ∗ 𝑐 = (7𝑥 103
𝐿
𝑚𝑜𝑙
) (1 𝑐𝑚) (5x10−5
) = 0.35
𝐿
𝑚𝑜𝑙 ∗ 𝑐𝑚
c) La transmitancia de las soluciones descritas en a) y b).
𝑇(𝑎) = 10−𝐴 = 10−0.175 = 0.6683
𝑇(𝑏) = 10−𝐴 = 10−0.35 = 0.4466
d) La absorbancia de una solución que tiene una transmitancia de la mitad de la que se describa
en a).
0.6683
= 0.33415
2
𝐴 = − log10(𝑇) = − log10 (0.33415) = 0.4760
17.
Una alícuota de 2.50 mL de una solución contiene 3.8 ppm de hierro (III) se trata con un exceso
de KSCN y se diluye hasta 50.0 mL. ¿Cuál es la absorbancia de la solución resultante a 580 nm en
una celda de 2.50 cm?
#𝑚𝑜𝑙𝑒𝑠 𝐹𝑒 = (3.8
𝑚𝑔
1𝑔
1 𝑚𝑜𝑙
)(
) (0.0025 𝐿) (
) = 1.7011𝑥 10−7𝑚𝑜𝑙
55.845 𝑔
𝐿
1000 𝑚𝑔
𝑀=
1.7011𝑥 10−7 𝑚𝑜𝑙
𝑚𝑜𝑙
= 3.4022𝑥 10−6
0.05 𝐿
𝐿
P á g i n a 13 | 19
𝐴 = 𝜀 ∗ 𝑙 ∗ 𝑐 = (7𝑥 103
18.
𝐿
𝑚𝑜𝑙
) (2.5 𝑐𝑚) (3.4022𝑥 10−6 𝐿 ) = 0.0595
𝑚𝑜𝑙 ∗ 𝑐𝑚
Una solución que contiene un complejo formado entre Bi (III) y tiourea tiene una absortividad
molar de 9.32x103 L mol-1cm-1 a 470 nm.
a) ¿Cuál es la absorbancia de una solución 6.24x10-5 M del complejo a 470 nm en una celda de 1.00
cm?
𝐴 = 𝜀 ∗ 𝑙 ∗ 𝑐 = (9.32x103
𝑚𝑜𝑙
𝐿
) (1 𝑐𝑚) (6.24x10−5
) = 0.5815
𝐿
𝑚𝑜𝑙 ∗ 𝑐𝑚
b) ¿Cuál es el porcentaje de transmitancia de la solución descrita en a)?
%𝑇 (𝑎) = (10−𝐴 ∗ 100) = (10−0.5815 ∗ 100) = 26.21%
c) ¿Cuál es la concentración molar del complejo en una solución que tiene la misma absorbancia
que en a), cuando se mide a 470 nm en una celda de 5.00 cm?
𝑐=
19.
0.5815
𝐴
𝑚𝑜𝑙
=
= 1.2478𝑥 10−5
𝐿
𝜀 ∗ 𝑙 (9.32x103
𝐿
𝑚𝑜𝑙 ∗ 𝑐𝑚) (5 𝑐𝑚)
El complejo formado entre Cu(I) y 1,10-fenantrolina tiene una absortividad molar de 7000 L
mol-1cm-1 a 435 nm, la longitud de onda para la máxima absorción. Calcular:
a) La absorbancia de una solución de 8.5x10-1 M del complejo cuando se mide una celda de 1.00
cm a 435 nm.
𝐴 = 𝜀 ∗ 𝑙 ∗ 𝑐 = (7000
𝐿
𝑚𝑜𝑙
) (1 𝑐𝑚) ( 8.5x10−1
) = 5950
𝐿
𝑚𝑜𝑙 ∗ 𝑐𝑚
b) El porcentaje de transmitancia de la solución en a).
%𝑇 (𝑎) = (10−𝐴 ∗ 100) = ( 10−5950 ∗ 100) = 0%
c) La concentración de una solución que es una celda de 5.00 cm tiene la misma absorbancia que
la solución a).
P á g i n a 14 | 19
𝑐=
𝐴
=
𝜀 ∗ 𝑙 (7000
5950
𝐿
= 0.17
𝑚𝑜𝑙
𝐿
(5 𝑐𝑚)
𝑚𝑜𝑙
∗ 𝑐𝑚 )de
d) La longitud de la trayectoria de la radiación
a través
una solución de 3.4x10-5 M del complejo
que se necesita para la absorbancia sea igual que la solución a).
𝑙=
20.
𝐴
=
𝜀 ∗ 𝑐 (7000
5950
= 25000 𝑐𝑚
𝐿
−5 𝑚𝑜𝑙 )
)
(
3.4x10
𝐿
𝑚𝑜𝑙 ∗ 𝑐𝑚
Una solución tiene una absorbancia “real” [𝐴 = log ( 𝑃0)] de 2.10 se colocó en un
𝑃
espectrofotómetro que tenía un nivel de radiación parásita (𝑃 𝑆) de 0.75%. ¿Qué absorbancia A’ se
𝑃
0
mediría? ¿Cuál sería el porcentaje de error?
%𝑇
𝐴´ = − log (
)
100
𝐴´ = − log (
%𝐸𝑟𝑟𝑜𝑟 =
0.75
)
100
𝐴´ = 2.1249
|𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎 𝑟𝑒𝑎𝑙 − 𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎 ℎ𝑎𝑙𝑙𝑎𝑑𝑎|
∗ 100
𝐴𝑏𝑠𝑜𝑟𝑏𝑎𝑛𝑐𝑖𝑎 𝑟𝑒𝑎𝑙
%𝐸𝑟𝑟𝑜𝑟 =
|2.10 − 2.1249|
∗ 100
2.10
%𝐸𝑟𝑟𝑜𝑟 = 1.1857 %
21.
El método común para determinar fósforo en orina consiste en tratar a la muestra con
molibdeno (VI) tras eliminar las proteínas y posterior reducción del complejo 12-molibdenofosfato
con ácido ascórbico. Las especies reducidas le imparten a la solución de un color azul intenso
P á g i n a 15 | 19
llamado azul de molibdeno, cuya absorbancia puede medirse a 650 nm. Una muestra de orina de
1122mL. Una alícuota de 1mL de la muestra se trató con Mo (VI) y ácido ascórbico y se diluyo hasta
un volumen de 50 mL. Se preparó una curva de calibración con alícuotas de 1mL de soluciones
patrón de fosfato tratadas igual que la muestra de orina. Las absorbancias de las soluciones patrón
y la muestra, medidas a 650 nm fueron las siguientes:
Solución
Absorbancia a 650 nm
1 ppm P
0.230
2 ppm P
0.436
3 ppm P
0.638
4 ppm P
0.848
0.518
Muestra de orina
a) Encuentre la pendiente, la ordenada al origen y el error estándar en “y” de la curva de
calibración.
(y = mx + b)
y = 0.2056x + 0.024
Pendiente: 0.2056
Ordenada al origen: 0.024
𝑥 =
0.230 + 0.436 + 0.638 + 0.848
= 0.538
4
[(0.230 − 0.538)2 + (0.436 − 0.538)2 + (0.638 − 0.538)2 + (0.848 − 0.538)2 ]
𝑆=√
4−1
𝑆 = 0.2654
P á g i n a 16 | 19
𝐷𝑒𝑠𝑣. 𝐸𝑠𝑡𝑎𝑛𝑑á𝑟
𝐸𝑟𝑟𝑜𝑟 𝑒𝑠𝑡á𝑛𝑑𝑎𝑟 =
=
√𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑚𝑢𝑒𝑠𝑡𝑟𝑎𝑠
Error estándar en “y”: 0.1328
0.2654 = 0.1328
√4
b) Grafique una curva de calibración
Absorbancia
Absorbancia en función de las soluciones patrón
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
y = 0.2056x + 0.024
R² = 0.9999
0
1
2
3
4
5
Concentración (ppm)
c) Determine la concentración de fósforo en ppm en la muestra de orina y su desviación estándar
a partir de la ecuación de los mínimos cuadrados de la línea. Compare la concentración
desconocida con aquella obtenida manualmente con la curva de calibración.
𝐴 = 𝑚𝑐 + 𝑏
𝐴 = 0.2056𝑐 + 0.024
0.518 = 0.2056𝑐 + 0.024
0.518 − 0.024 = 0.2056𝑐
𝑐=
0.518 − 0.024
0.2056
𝑐 = 2.4027 𝑝𝑝𝑚 𝑑𝑒 𝑃 𝑒𝑛 𝑙𝑎 𝑚𝑢𝑒𝑠𝑡𝑟𝑎 𝑑𝑒 𝑜𝑟𝑖𝑛𝑎
𝐷𝑒𝑠𝑣𝑖𝑎𝑐𝑖ó𝑛 𝑒𝑠𝑡á𝑛𝑑𝑎𝑟 = 0.2654
P á g i n a 17 | 19
22.
El nitrito se determina comúnmente mediante un análisis colorimétrico que se basa en una
reacción de Griess. En esta reacción, la muestra con nitrito se hace reaccionar con sulfanilamida y
N-(1-naftil) etilendiamina, dando un compuesto colorido que absorbe a 550 nm. Utilizando un
instrumento de análisis automatizado de flujo, se obtuvieron los siguientes resultados para las
soluciones patrón de nitrito y la muestra con una cantidad desconocida.
Solución
Absorbancia a 550 nm
2.00 μM
0.065
6.00 μM
0.205
10.00 μM
0.338
14.00 μM
0.474
18.00μM
0.598
Desconocido
0.402
a) Obtener la pendiente y la intersección de la curva de calibración, así como el error estándar de
“y”.
y= 0.0334x + 0.0023
Pendiente = 0.0334
Intersección: (0, 0.0023)
𝑥 =
0.065 + 0.205 + 0.338 + 0.474 + 0.598
= 0.336
5
[(0.065 − 0.336)2 + (0.205 − 0.336)2 + (0.338 − 0.336)2 + (0.474 − 0.336)2 + (0.598 − 0.336)2 ]
𝑆=√
5−1
𝑆 = 0.2111
P á g i n a 18 | 19
𝐸𝑟𝑟𝑜𝑟 𝑒𝑠𝑡á𝑛𝑑𝑎𝑟 =
𝐷𝑒𝑠𝑣. 𝐸𝑠𝑡𝑎𝑛𝑑á𝑟
√𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑚𝑢𝑒𝑠𝑡𝑟𝑎𝑠
=
Error estándar en “y”: 0.0944
0.2111 = 0.0944
√5
b) Construir un gráfico de la curva de calibración.
Absorbancia en función de las soluciones patrón
0.7
Absorbancia
0.6
y = 0.0334x + 0.0023
R² = 0.9996
0.5
0.4
0.3
0.2
0.1
0
0
5
10
15
20
Concentración (μM)
c) Determinar la concentración de nitrito en la muestra y su desviación estándar.
y= 0.0334x + 0.0023
𝐴 = 𝑚𝑐 + 𝑏
𝐴 = 0.0334𝑐 + 0.0023
0.402 = 0.0334𝑐 + 0.0023
0.402 − 0.0023 = 0.0334𝑐
𝑐=
0.402 − 0.0023
0.0334
𝑐 = 11.9670 𝜇𝑀 𝑑𝑒 𝑛𝑖𝑡𝑟𝑖𝑡𝑜 𝑒𝑛 𝑙𝑎 𝑚𝑢𝑒𝑠𝑡𝑟𝑎
Desviación
Estándar
0.2111
P á g i n a 19 | 19