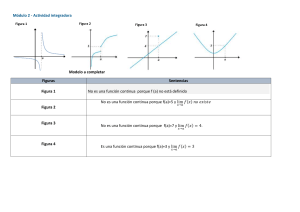
pdfslide.tips tema25lmites-de-funciones-continuidad-y-25pdf-tema-25-lmites-de-funciones

TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
TEMA25.Límites de funciones. Continuidad y discontinuidades.
Teorema de Bolzano. Ramas Infinitas
1. Introducción
La continuidad es una de las propiedades más importantes que definen a una función. Muchos teoremas del análisis funcional se apoyan en la continuidad de las funciones. Conceptualmente una función es continua en un intervalo [a,b] si en está definida en cada punto del
intervalo y no se producen saltos en su representación.
La mayoría de las situaciones en la Naturaleza describen situaciones entre dos o más variables que se relacionan por funciones de forma continua. Los fenómenos físicos desde un
punto de vista macroscópico siguen la mecánica Newtoniana, que es continua (así si empujamos un cuerpo desde el reposo hasta una velocidad máxima este pasa por todas las velocidades reales que hay entre ambas).
Existen funciones en la Naturaleza que no son continuas, la mayoría de ellas son debidas a
cambios de contorno. Así por ejemplo el campo eléctrico creado por un conductor en función
de las distancia del centro no es continuo, pues en su interior es nulo y en la superficie es
σ
ε0
Para describir la continuidad previamente hay que describir el límite de una función en un
punto, que explica el comportamiento de dicha función en un entorno del punto. Los límites
en la naturaleza se utilizan para explicar el comportamiento en puntos inalcanzables, un ejemplo típico es el estudio de las propiedades termodinámicas en el cero absoluto (0K).
Históricamente el concepto de límite y continuidad recibieron una formulación precisa en
el siglo XIX especialmente realizados por Cauchy, y están estrechamente ligados al concepto
matemáticos del número real.
2. Límite de una función
2.1.Conceptos previos. Función real
Una función f, es una correspondencia entre D⊆ℝ y ℝ definida de la forma:
f: D
x
→ ℝ
→ y= f(x)
y tal que ∀x∈D se cumple que f(x) es único.
La variable x se denomina independiente y el conjunto de todos los puntos x∈D se denomina dominio de la función Dom(f). La variable y se denomina dependiente y el conjunto de
valores de y= f(x) se denomina recorrido, rec (f)={y∈ ℝ : f(x)=y, ∀x∈ ℝ }.
2.2. Definición de límites finitos.
Una función real f(x) se dice que tiene límite l∈ ℝ cuando x tiende a un valor a∈ ℝ, y se
denota como
lim f ( x ) = l si se cumple ∀ε>0 ∃ δ>0: 0<|x-a|<δ |f(x)-l|<ε
x→a
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
1
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
Conceptualmente implica que si definimos un entorno
de f alrededor de l (|f(x)-l|<ε)) siempre podemos enconenco
trar un entorno de x=a (|x-a|<δ)) donde los valores de la
imagen en el entorno de f antes definido.
En la mayoría de funciones los valores de los límites
coinciden con el valor de la función en dicho punto
(concepto que como veremos describe la continuidad),
pero existen funciones donde esto no ocurre como vev
remos a continuación.
Ejemplos de límites:
1) f(x)=c·x,
lim f ( x ) = c·a . Demostración ∀ε>0 ∃ δ>0: 0<|x-a|<δ
x→a
|c·x-c·a|<ε,
|c|·|x-a|<ε,, luego tomando δ<ε/|c|
/|c| se cumple la desigualdad anterior.
En este caso f(a)= lim f ( x )
x→ a
c·x si x ≠ 0
podemos demostrar que
 3 si x = 0
2) Si definimos ahora la función f ( x) = 
lim f ( x ) = 0 de igual forma que en 1) pues x en el entorno de cero no es cero. Pero
x →0
ahora a diferencia con 1) f(0)=3≠ lim f ( x ) = 0
x →0
2.2.1. Límites lateral
laterales
En la definición de límite no hemos diferenciado entre la aproximación al punto x=a “por la
izquierda” (valores inferiores de a, x<a) o “por la derecha” (valores mayores de a, x>a). Vamos
a definir ahora de forma matemática los denominados límites later
laterales.
Una función real f(x) se dice que tiene límite de valor l cuando x tiende hacia a por la izquierda y se denota
l|<ε
lim f ( x ) = l si cumple ∀ε>0 ∃ δ>0: ∀x∈(a-δ,a) |f(x)-l|<
x→a −
Una función real f(x) se dice que tiene límite de valor l cuando x tiende hacia a por la derecha y se denota
l|<ε
lim f ( x ) = l si cumple ∀ε>0 ∃ δ>0: ∀x∈(a,a+δ) |f(x)-l|<
x→a +
1
2
Ejemplo f ( x) = 
si x ≥ 0
si x < 0
lim f ( x ) = 2
x →0 −
2
lim f ( x ) = 1
x →0 +
1
Jose Luis Lorente (preparador oposiciones secund
secundaria www.joseluislorente.es)
2
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
Proposición: la función real f(x) tiene límite en x=a si y sólo si existen los dos límites laterales y son iguales.
Demostración:
⇒ si se cumple que lim f ( x ) = l implica que ∀ε>0 ∃ δ>0: 0<|x-a|<δ |f(x)-l|<ε por lo
x→a
tanto se cumple en x∈(a-δ,a+δ) y por tanto en x∈(a-δ,a) y x∈(a,a+δ) y por tanto cumple
•
∀ε>0 ∃ δ>0: ∀x∈(a-δ,a) |f(x)-l|<ε por tanto lim− f ( x ) = l
•
∀ε>0 ∃ δ>0: ∀x∈(a,a+δ) |f(x)-l|<ε por tanto lim+ f ( x ) = l
x→a
x→a
⇐ sean lim− f ( x ) = lim+ f ( x ) = l , entonces se cumple:
x→ a
x→a
•
∀ε>0 ∃ δ1>0: ∀x∈(a-δ1,a) |f(x)-l|<ε por tanto lim− f ( x ) = l
•
∀ε>0 ∃ δ2>0: ∀x∈(a,a+δ2) |f(x)-l|<ε por tanto lim+ f ( x ) = l
x→a
x→a
Tomando δ=min{δ1, δ2} cumple ∀ε>0 ∃ δ>0: ∀x∈(a-δ,a+δ) |f(x)-l|<ε por tanto lim f ( x ) = l
x→a
lim f ( x ) = l
x→a −
lim f ( x ) = l
x→a
1+ε
1-ε
1-δ1
1+ε
1-ε
1-δ
1+δ
lim f ( x ) = l
x→a +
1+ε
1-ε
1+δ2
Explicación gráfica de la demostración
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
3
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
2.2.2. Propiedades de los límites
Proposición 1: si una función f(x) es real tiene límite en un punto x=a entonces la función
está acotada en un entorno de a.
Demostración: si se cumple lim f ( x ) = l ∀ε>0 ∃ δ>0: 0<|x-a|<δ |f(x)-l|<ε, tomanx→a
do ε=1, entonces ∃ δ>0: 0<|x-a|<δ |f(x)-l|<1 luego en (a-δ,a+δ) la función f(x) acotada
inferiormente por l-1 y superiormente por l+1.
Proposición 2: si una función f(x) tiene límite en un punto x=a este límite es único.
Demostración: lo haremos por reducción a lo absurdo: supongamos que tiene dos límites
l1≠l2, es decir
•
lim f ( x ) = l1 ∀ε>0 ∃ δ1>0: 0<|x-a|<δ |f(x)-l1|<ε
•
lim f ( x ) = l 2 ∀ε>0 ∃ δ2>0: 0<|x-a|<δ2 |f(x)-l2|<ε
x→a
x→a
| f (x) −l1 |< ε
|l1-l2|=|l1-f(x)-(l2-f(x)|≤|l1-f(x)|+ |l2-f(x)|<2 ε
| f (x) −l2 |< ε
Sea δ=min{δ1,δ2} en <|x-a|<δ 
Se cumple así que |l1-l2|<2 ε ∀ ε >0 ⇔| l1-l2|=0, es decir l1=l2 que contradice la hipótesis.
2.2.3. Álgebra de límites
Se cumplen las siguientes propiedades (sean lim f ( x ) = l1 , lim g ( x ) = l 2 )
x→a
x→a
1. Suma y resta: lim f ( x ) + g ( x ) = l1 + l 2
x→a
2. Producto lim f ( x )·g ( x ) = l1·l 2
x→a
3. División: lim
x→a
f ( x) l1
=
g ( x) l 2
Demostraciones: utilizaremos lim f ( x ) = l1 ∀ε>0 ∃ δ1>0: 0<|x-a|<δ |f(x)-l1|<ε y
x→a
lim g ( x ) = l 2 ∀ε2>0 ∃ δ2>0: 0<|x-a|<δ2 |g(x)-l2|<ε2
x→a
1.
Tomando ∀ε>0 δ=min(δ1,δ2): |f(x)+g(x)-(l1+l2)|≤|f(x)-l1|+|g(x)-l2|<ε1+ε2=ε. Luego
cumple definición de lim f ( x ) + g ( x ) = l1 + l 2
x→a
2.
Al existir límite f(x) acotada por K superiormente en entorno de a (f(x)<a) Tomando
|f(x)·g(x)-(l1·l2)|=|f(x)·g(x)-f(x)l2+f(x)·l2-l1·l2|≤|f(x)|·|g(x)∀ε>0
δ=min(δ1,δ2):
l2|+l2·|f(x)-l1|<K·ε2+l2·ε1=ε. Luego cumple definición de lim f ( x )·g ( x ) = l1·l 2
x→a
3.
Se cumple al existir limites que f(x)≤K1 y g(x)≥k2≠0 Tomando ∀ε>0 δ=min(δ1,δ2):
f ( x)·l 2 − g ( x)·l1 + f ( x)·g ( x) − f ( x) g ( x)
f ( x)·l 2 − g ( x)·l1
f ( x) l1
− =
=
≤
g ( x) l 2
g ( x)·l 2
k 2 ·l 2
≤
1
f ( x) l1
(| K1 || g ( x) − l 2 | + | k 2 || f ( x) − l1 |) ≤ | K1·ε 2 | + | k 2 ·ε 1 | = ε → lim
=
x
→
a
k 2 ·l 2
k 2 ·l 2
g ( x) l 2
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
4
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
2.3. Límites Infinitos
2.3.1. Ampliación de ℝ.
Para definir los límites infinitos primero tenemos que describir el concepto de infinito, para
luego ampliar el conjunto de los números reales e incluir el infinito en este nuevo conjunto:
= ℝ ∪ {∞, −∞} con ±∞ definidos de la siguiente forma -∞<x<∞ ∀x∈∈ ℝ (idea intuitiva)
ℝ
Operaciones con ±∞
1)
Suma y resta en ℝ
• (x±∞)=±∞ +x=±∞
• x-(±∞) = ∓∞
• ∞+∞=∞
•-∞ − ∞ = −∞
Indeterminaciones: ∞ − ∞ y −∞ + ∞
(suponemos x∈ ℝ+)
2) Producto en ℝ
• x·(±∞) = ±∞
• -x·(±∞) = ∓∞
• (±∞)·(±∞) = ∞
• (±∞)·(∓∞) = −∞
Indeterminaciones: (±∞) · 0 y 0·(±∞)
(suponemos x∈ ℝ+)
3) Cociente en ℝ
•
±
•
=0
Indeterminaciones:
± , ,
± 4) Potencia en
ℝ
∞
• si x>1 x =∞ y x-∞=0
±
•
= ±∞
±
= ∓∞
para todo x∈ℝ
• si 0<x<1
x∞=0 y x-∞=∞
Indeterminaciones 0∞, 1∞, 00, ∞0
2.3.2. Definiciones de límites infinitos
Definiciones:
1) Una función f(x) tiende a ∞ cuando x tiende hacia “a” y se denota → () = ∞ si
se cumple ∀M>0 ∃ δ>0 : x∈(a-δ,a+δ) → f(x)>M
2) Una función f(x) tiende a -∞ cuando x tiende hacia “a” y se denota → () = −∞
si se cumple ∀m<0 ∃ δ>0 : x∈(a-δ,a+δ) → f(x)<m
3) Una función f(x) tiende a “l” cuando x tiende hacia ∞ y se denota → () = si
se cumple ∀ε>0 ∃ K>0 : x>K → |f(x)-l|<ε
4) Una función f(x) tiende a “l” cuando x tiende hacia -∞ y se denota → () = si
se cumple ∀ε>0 ∃ k<0 : x<k → |f(x)-l|<ε
5) Una función f(x) tiende a ∞ cuando x tiende hacia ∞ y se denota → () = ∞ si
se cumple ∀M>0 ∃ K>0 : x>K → f(x)>M
6) Una función f(x) tiende a -∞ cuando x tiende hacia ∞ y se denota → () = −∞
si se cumple ∀m<0 ∃ K>0 : x>K → f(x)<m
7) Una función f(x) tiende a ∞ cuando x tiende a -∞ y se denota → () = ∞ si se
cumple ∀M>0 ∃ k<0 : x<k→ f(x)>M
8) Una función f(x) tiende a -∞ cuando x tiende a -∞ y se denota → () = −∞ si
se cumple ∀m<0 ∃ k<0 : x<k→ f(x)<m
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
5
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
Interpretación gráfica
lim→" #($) = ∞ y lim→" #($) = −∞
1) y 2)
3) y 4) lim→ #($) = 2 , lim→ #($) = −2
5) y 7) lim→ #($) = ∞ y lim→ #($) = ∞
6) y 8) lim→ #($) = −∞ y lim→ #($) = −∞
Ejemplos analíticos:
•
•
•
"
"
'
lim→ ||=∞ ∀M>0 tomamos δ<
se cumple si x∈(-δ,δ) →f(x)>M
(
lim→ $ =∞ ∀M>0 tomamos K>)* se cumple si x>K →f(x)>M
"
"
lim→ =0 ∀ε>0 tomamos M>+ se cumple si x>M→ |f(x)-0|<ε
2.3.3. Resolución indeterminaciones
Caso 1: ∞-∞. Domina el que tienda a ∞ más rápido el orden de crecimiento de menor a mayor
en infinito es de la siguiente forma (donde > indica que domina su crecimiento en x∞)
•
log(x)> xn>kx>xx
dentro de xn crecimiento mayor cuanto mayor sea n y dentro de
(
kx mayor el crecimiento cuanto mayor k. Ej: lim x − ln( x) + 2
x →∞
•
2
x
) = lim 2
x →∞
x
=∞
En caso de que el crecimiento sea el mismo y no se pueda operar (raíces) se multiplica por el conjugado quedando una indeterminación del tipo
lim
x→ ∞
(
x3 − x −
)
x 3 + 2 = lim
x→ ∞
(
x 3 − x − ( x 3 + 2)
x −x +
3
x +2
3
)
= lim
x→ ∞
∞
. Ejemplo:
∞
−x−2
x −x +
3
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
x +2
3
=
6
∞
∞
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
Caso 2: ∞/∞. Domina el que tienda a ∞ más rápido, pudiendo ocurrir:
a) Si domina el numerador límite es ±∞: lim
x→ ∞
∞
2 x − 3x
2x
=
= lim 4 = ∞
4
x→ ∞ x
∞
x
− x−2
b) Si domina numerador límite es 0: lim
x→∞
x3 − x + x3 + 2
=
∞
−x
−1
= lim
= lim
=0
∞ x→∞ 2 x 3 x→∞ 2 x
3
3
c) Si el crecimiento es el mismo, cociente coeficientes: lim 2 x3 − 32x + 3 = lim 2 x3 = 2
x →∞ 5 x − x + 4
x →∞ 5 x
5
2
−
∞
1
x
3
x
2
=
=∞
( x − 3 x )· = ∞·0 = lim
Caso 3: ∞·0 se transforma en ∞/∞: lim
x→ ∞
x→ ∞
∞
x
x
(x +1)(x −1)
(x +1)
x 2 −1 0
= = lim
= lim
=2
x→1 x −1
x→1
0 x→1 (x −1)
1
Caso 4: 0/0 se calcula factorizando por la raíz: lim
Caso 5: k/0 factorizar denominador y tomar límites laterales (límite puede ser ±∞ o no existir):
•
x+2
3

= − = −∞
lim−

x+2
x+2
3  x →1 ( x − 1)( x + 1) 0 ·2
= lim
= =
lim 2
No existe
x →1 x − 1
x →1 ( x − 1)( x + 1)
x+2
3
0  lim
=
=
∞
+
+
 x →1 ( x − 1)( x + 1) 0 ·2
•
x+3
2

lim−
=
=∞
2
2

−
x+3
x+3
2  x → −1 ( x + 1)
0
·
2
lim
=∞
= lim
= =
x → −1 x 2 + 2 x + 1
x →1 ( x + 1) 2
x+3
3
0 
lim
= + 2 =∞
 x →−1+ ( x + 1) 2
0 · 2
( )
( )
x
 x+2 
∞
 =0 ,
x →∞ x 2 − x


Caso 6: 1∞, 0∞, ∞0, 00: se calcula tomando logaritmos a ambos lados: l = lim
 x+2 
ln(l) = limx·ln 2  = limx· ln(x + 2) − ln(x2 − x) = limx·(ln(x) − 2ln(x)) = ∞·(−∞) = −∞ → l=e-∞=0
x→∞
x→∞
 x − x  x→∞
(
)
3. Funciones continuas.
3.1.Continuidad puntual.
Una función real f(x) es continua en un punto x=a cuando se cumple lim f ( x ) = f ( a ) .
x→a
Podemos hablar de continuidad lateral, siendo continua por la izquierda si lim− f ( x ) = f ( a )
x→a
y por la derecha si lim+ f ( x ) = f ( a ) . Evidentemente para que la función sea continua en x=a
x→a
tiene que serlo por la izquierda y por la derecha.
3.2.Continuidad en un intervalo
Una función f(x) continua en un intervalo (a,b)⊆dom(f(x)) cuando lo es en todo punto del
intervalo, es decir ∀x0∈(a,b) lim f ( x) = f ( x0 ) .
x → x0
Una función f(x) continua en un intervalo [a,b]⊆dom(f(x)) cuando lo es en todo punto del
intervalo (a,b), es decir ∀x0∈(a,b) lim f ( x) = f ( x0 ) y además continua por la derecha en
x → x0
x=a y por la izquierda en x=b ( lim+ f ( x ) = f ( a ) , lim− f ( x) = f (b ) )
x→a
x →b
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
7
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
Una función f(x) continua en un intervalo [a,b) ( o en (a,b]) cuando lo es en todo punto del
intervalo (a,b), es decir ∀x0∈(a,b) lim f ( x) = f ( x0 ) y además continua por la derecha en
x → x0
x=a (por la izquierda en x=b).
3.3.Álgebra de funciones continuas.
Proposición: sean f(x) y g(x) funciones continuas en x=a entonces se cumple que (1)
(f±g)(x), (2) (f·g)(x), (3) (f/g)(x) son continuas en x=1.
Demostraciones:
1) lim( f + g )( x ) = f ( a ) + g ( a ) = ( f + g )( a )
x→a
2) lim( f ·g )( x ) = f ( a )·g ( a ) = ( f ·g )( a )
x→a
3) lim( f / g )( x ) = f ( a ) / g ( a ) = ( f / g )( a )
x→a
Corolario 1: Podemos extender el planteamiento para la suma y/o producto de más de dos
n
n
funciones continuas en x=a: ∀ fi continuas en x=a →
∑ f ( x) ∏ f ( x) continua en x=a.
i
i
i =1
i =1
Corolario 2: Como f(x)=x continua en ℝ entonces toda función polinómica f(x)=an·xn+…+a0
es también continua en ℝ.
Corolario 3: Se cumple que el conjunto de las funciones continuas en D⊆ ℝ con las operaciones suma y producto escalar, denotadas como (C0(D),+,·) es un subespacio de las funciones
reales definidas en D, ( F(D),+,·).
Demostración: tanto la suma como el producto (en particular por las funciones constantes)
es cerrado en las funciones continuas, por tanto es subespacio.
4. Propiedades de las funciones continuas en un punto.
4.1.Acotación de la función en torno al punto.
Proposición: si una función real f(x) es continua en un punto x=a entonces esta función
acotada en torno a este punto.
Demostración: aplicamos la definición de continuidad lim f ( x ) = f ( a ) , luego al existir el
x→a
límite tomando ε=1 ∃ δ>0: |x-a|<δ se cumple |f(x)-f(a)|<1, por tanto f(a)-1<f(x)<f(a)+1 en un
entrono de x=a, x∈(a-δ,a+δ).
4.2.Conservación del signo de la función en un entorno de un punto.
Proposición: sea f(x) una función continua en x=a, tal que f(a)≠0 entonces existe un entorno de x=a donde la función conserva el signo, es decir si f(a)>0 la función es positiva, y si f(a)<0
la función es negativa.
Demostración: veremos sólo el caso f(a)>0 pues el otro es equivalente. Por definición de
continuidad ∀ε>0 ∃ δ>0: x∈(a-δ,a+δ) → |f(x)-f(a)|<ε. Tomando el valor de ε=f(a)/2 se cumple:
x∈(a-δ,a+δ) → |f(x)-f(a)|<f(a)/2, luego f(a)-f(a)/2<f(x)<f(a)+f(a)/2, luego f(x)>0 en x∈(a-δ,a+δ).
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
8
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
5. Propiedades de las funciones continuas.
5.1.Teorema de Bolzano
Teorema de Bolzano: sea f(x) una función continua en [a,b] y tal que f(a)·f(b)<0 (cambia de
signo) existe al menos un c∈(a,b) donde se cumple f(c)=0.
Demostración: supondremos que f(a)>0 y f(b)<0 (sino se demuestra de forma equivalente).


Dividimos el intervalo en dos:  a,
a + b
a + b 
= [a, c1 ] y 
, b  = [c1 , b ] , si se cumple que

2 

 2
f(c1)=0 hemos demostrado el teorema, sino tomamos el intervalo donde los extremos cambien
el signo. Se vuelve a dividir el intervalo en el punto el punto medio, c2, si f(c2)=0 se cumple el
teorema siendo c=c2 y se termina el teorema. Si no volvemos a coger el intervalo con extremos
de diferente signo. Repetimos el procedimiento de forma paulatina pudiendo ocurrir:
1. Que en algún punto cn cumpla f(cn)=0 y entonces cumple el teorema.
2. No se anula nunca, con lo que construiremos intervalos encajados con extremos de diferente signo y cada vez más pequeños (cada paso el intervalo mide la mitad del anterior): [a,b] con f(a)·f(b)<0; [a1,b1] con f(a1)·f(b1)<0,…, [an,bn] con f(an)·f(bn)<0. El límite
de los intervalos encajados es un punto ∩[an,bn]=lim(an)=lim(bn)=c que cumple f(c)≤0 y
f(c) ≥0, luego f(c)=0.
Gráficamente:
5.2.Teorema del valor intermedio (Darboux)
Teorema de Darboux: Sea f una función real continua en [a,b] entonces f toma todos los
valores comprendidos ente f(a) y f(b). Es decir ∀ α∈ℝ con f(a)<α<f(b) o f(b)<α<f(a) se cumple
existe al menos un c∈(a,b) tal que f(c)=α.
Demostración: supongamos f(a)<α<f(b) (demostración equivalente si f(b)<α<f(a)). Definimos la función g(x)=f(x)-α que será continua en [a,b] y se cumple g(a)=f(a)-α<0 y g(b)=f(b)-α>0
y por tanto g(x) cumple Bolzano, y por tanto ∃ c∈[a,b]: g(c)=f(c)-α=0, y por tanto f(c)=α.
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
9
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
5.3.Teorema de acotación (Weierstrass)
Teorema de la acotación: Sea f(x) una función continua en [a,b] entonces f(x) acotado en
[a,b] y tiene un máximo y un mínimo. Es decir existen dos puntos c,d∈[a,b] tal que
f(c)=sup{f(x): x∈[a,b]} y f(d)=inf{f(x):x∈[a,b]}
Demostración: por reducción a lo absurdo, llamamos s=sup{f(x): x∈[a,b]} y supondremos
que no existe x∈[a,b] donde f(x)=s. Se cumple que la función g ( x ) =
1
será continua
s − f ( x)
al no anularse el denominador y ser f(x) continua. Al ser continua g(x) acotada, y por tanto
∀x∈[a,b] donde g(x)<k →
1
1
< k → f ( x) < s − < s en x∈[a,b], luego s no es el sus − f ( x)
k
premo será s-1/k y contradice la proposición, y por tanto el supremo se toma en x∈[a,b]. De
igual forma para el ínfimo.
6. Tipos de discontinuidades en una función.
Decimos que una función f(x) es discontinua en x0 ∈D si no es continua en dicho punto y
por tanto no cumple lim f ( x) = f ( x0 )
x → x0
Existen varias clasificaciones de los tipos de discontinuidades de una función, una de las
más extendida es la siguiente:
1. Evitable: existe el límite lim f ( x) = c y no existe el f(x0) o el valor de f(x0)≠c. Se llama
x → x0
 f ( x) si x ≠ x0
esta
si x = x0
c
así porque redefiniendo la función en x0 de la forma f ( x) = 
se vuelve continua. Ejemplos:
Jose Luis Lorente (preparador oposiciones secundaria www.joseluislorente.es)
10
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
2. Discontinuidad de salto finito
finito: el límite en x0 no existe por ser distintos los límites latelat
rales.
3. Discontinuidad de salto infinito
infinito: el límite en x0 no existe por ser uno de los dos límites
laterales o los dos infin
infinitos.
7. Ramas infinitas.
finitas. Asíntotas
Una asíntota es una recta a la que la función se acerca a ella sin llegar a tocar, coincidiendo
el comportamiento de la función con la recta en el infinito. Tres tipos de asíntotas:
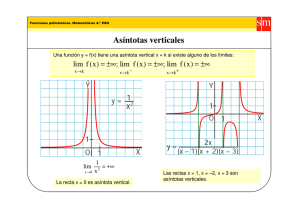
a) Asíntota vertical:: es una recta x=x0 y ocurre en los puntos
ntos de la función donde se cumcu
ple lim+ f ( x ) = ±∞ y/o lim+ f ( x ) = ±∞ , es decir tiene una discontinuidad de salto
x → x0
x → x0
infinito. Las asíntotas verticales son típicas de funciones con denominador, siendo las
asíntotas los valores que anulen el den
denominar
ominar (a no ser que también anulen el numenum
rador) y las funciones con logaritmo, siendo las asíntotas en este caso los valores que
anulen el argumento del logaritmo. Una función puede tener el número que se desee
de asíntotas verticales.
cales. Ejemplos:
Jose Luis Lorente (preparador oposiciones secund
secundaria www.joseluislorente.es)
11
TEMA 25. Límites de funciones. Continuidad y discontinuidad. Bolzano. Ramas infinitas
b) Asíntotas horizontales
tales:: son de la forma y=a. La función tiene asíntota si se cumple que
lim f ( x) = a1 (asíntota y=a1) y/o lim f ( x) = a2 (asíntota y=a2). Por tanto una funfu
x →∞
x →−∞
ción puede tener dos asíntotas, aunque generalmente el límite suele ser el mismo y si
tiene asíntota horizontal es única. Veamos un ejemplo con dos asíntotas:
x3 + 1
y= f ( x) = 3
| x +2|
lim f ( x ) = −1
x → −∞
lim f ( x ) = 1
x →∞
m≠0.
0. Una función f(x) tiene una asíntoasínt
c) Asíntota Oblicua:: son de la forma y=mx+n con m
ta oblicua cuando al tender a ∞ y/0 a -∞ la gráfica de esta función tiende
tien al de la recta.
En la práctica ocurre cuando m = lim
x →∞
f ( x)
f ( x)
∈ℝ* y n = lim
− mx ∈ℝ y lo mismo
x
→
∞
x
x
para el límite a -∞,, pudiendo tener así hasta dos asíntotas oblicuas, aunque lo normal
si tiene es que sea la misma para ±∞. Veamos un ejemplo con
on dos asíntotas oblicuas
8. Contexto con secundaria.
La continuidad se aborda de forma intuitiva en 3º y 4º de la ESO a partir de gráficas y funfu
ciones definidas a trozos, aunque en el currículo no incluye el concepto de límite.
límite
En bachillerato, en las dos ramas, es donde se trabajan los conceptos de límite y de conticont
nuidad, así como los teoremas vistos en el tema. Es además la continuidad y los límites una
prueba recurrente en la PAU.
Jose Luis Lorente (preparador oposiciones secund
secundaria www.joseluislorente.es)
12