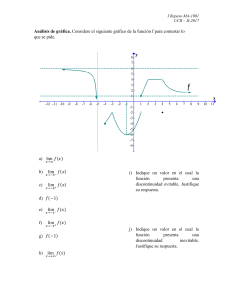
4 ( ) 3 x f x x - = + 4 ( ) 3 x f x x
Anuncio

Categoría B
Matemática
17/12/2014
x2 4
f ( x)
.Investiga dominio y signo y determina todas sus asíntotas
x3
i.
Dada
ii.
x2 4
Dada f ( x)
.Investiga crecimiento determinando extremos.
x3
iii.
Grafica una función que cumpla las siguientes condiciones:
Dom f R 0 , 2 y
lim f , lim f , lim f 0 , lim f 1, lim f
x2
x0
x2
x
x
2
iv.
v.
{𝑒 𝑥−2 − 2, 𝑠𝑖 𝑥 ≤ 2 Determina el valor de a para que la función sea continua en 2.
𝑥 2 + 𝑎, 𝑠𝑖 𝑥 > 2
Previamente define continuidad en un punto.
Define derivada. Aplica la definición de derivada para determinar f´(2) en la función
f(x)=𝑥 2 − 3. Determina además la ecuación de la recta tangente en ese punto.
Prueba para: Denis