anexo 1 geometria 11

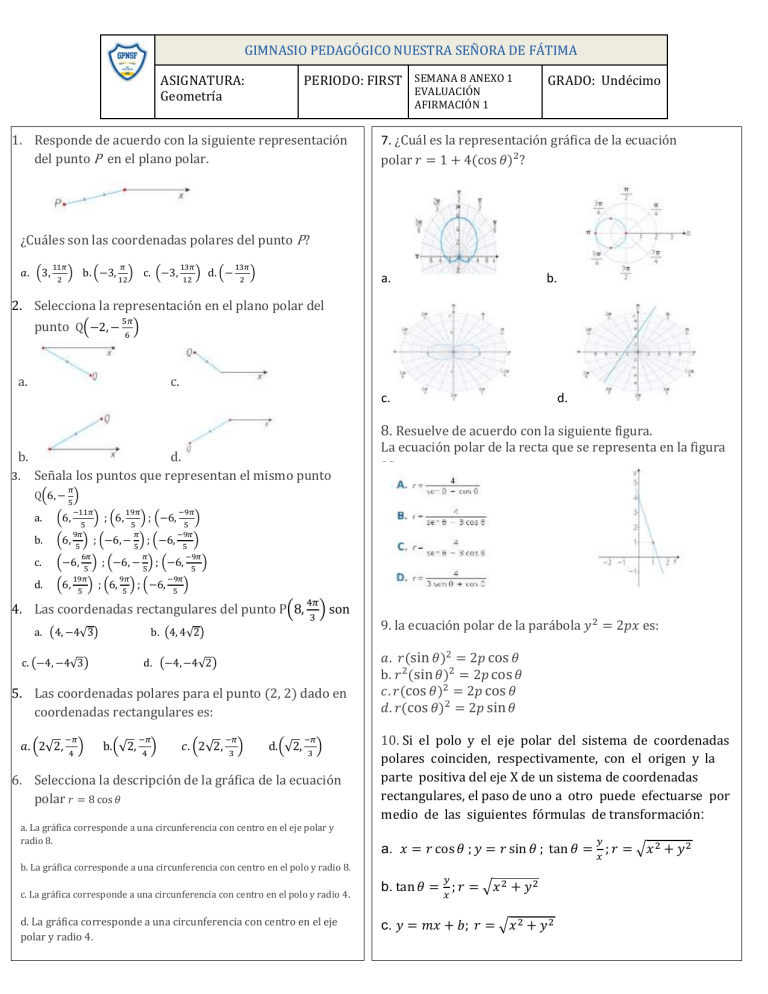
GIMNASIO PEDAGÓGICO NUESTRA SEÑORA DE FÁTIMA
PERIODO: FIRST SEMANA 8 ANEXO 1
ASIGNATURA:
Geometría
EVALUACIÓN
AFIRMACIÓN 1
1. Responde de acuerdo con la siguiente representación
del punto P en el plano polar.
GRADO: Undécimo
7. ¿Cuál es la representación gráfica de la ecuación
polar 𝑟 = 1 + 4(cos 𝜃)2?
¿Cuáles son las coordenadas polares del punto P?
𝑎. (3,
11𝜋
2
𝜋
13𝜋
12
12
) b. (−3, ) c. (−3,
) d. (−
13𝜋
2
)
a.
b.
2. Selecciona la representación en el plano polar del
5𝜋
punto Q(−2, − 6 )
a.
c.
c.
d.
8. Resuelve de acuerdo con la siguiente figura.
b.
3.
d.
Señala los puntos que representan el mismo punto
La ecuación polar de la recta que se representa en la figura
es:
𝜋
Q(6, − )
5
−11𝜋
a.
(6,
b.
(6,
c.
d.
5
9𝜋
(6,
19𝜋
5
𝜋
) ; (−6,
) ; (−6, − ) ; (−6,
5
(−6,
) ; (6,
−9𝜋
5
−9𝜋
5
6𝜋
5
19𝜋
5
𝜋
5
) ; (6,
5
) ; (−6,
−9𝜋
5
)
5
−9𝜋
) ; (−6, − ) ; (−6,
9𝜋
)
5
)
)
4. Las coordenadas rectangulares del punto P(8,
a. (4, −4√3)
4𝜋
)
3
son
b. (4, 4√2)
c. (−4, −4√3)
d. (−4, −4√2)
5. Las coordenadas polares para el punto (2, 2) dado en
coordenadas rectangulares es:
𝑎. (2√2,
−𝜋
4
)
b.(√2,
−𝜋
4
)
𝑐. (2√2,
−𝜋
3
)
d.(√2,
−𝜋
3
)
6. Selecciona la descripción de la gráfica de la ecuación
polar 𝑟 = 8 cos 𝜃
a. La gráfica corresponde a una circunferencia con centro en el eje polar y
radio 8.
9. la ecuación polar de la parábola 𝑦 2 = 2𝑝𝑥 es:
𝑎. 𝑟(sin 𝜃)2 = 2𝑝 cos 𝜃
b. 𝑟 2 (sin 𝜃)2 = 2𝑝 cos 𝜃
𝑐. 𝑟(cos 𝜃)2 = 2𝑝 cos 𝜃
𝑑. 𝑟(cos 𝜃)2 = 2𝑝 sin 𝜃
10. Si el polo y el eje polar del sistema de coordenadas
polares coinciden, respectivamente, con el origen y la
parte positiva del eje X de un sistema de coordenadas
rectangulares, el paso de uno a otro puede efectuarse por
medio de las siguientes fórmulas de transformación:
𝑦
a. 𝑥 = 𝑟 cos 𝜃 ; 𝑦 = 𝑟 sin 𝜃 ; tan 𝜃 = 𝑥 ; 𝑟 = √𝑥 2 + 𝑦 2
b. La gráfica corresponde a una circunferencia con centro en el polo y radio 8.
𝑦
c. La gráfica corresponde a una circunferencia con centro en el polo y radio 4 .
b. tan 𝜃 = 𝑥 ; 𝑟 = √𝑥 2 + 𝑦 2
d. La gráfica corresponde a una circunferencia con centro en el eje
polar y radio 4.
c. 𝑦 = 𝑚𝑥 + 𝑏; 𝑟 = √𝑥 2 + 𝑦 2