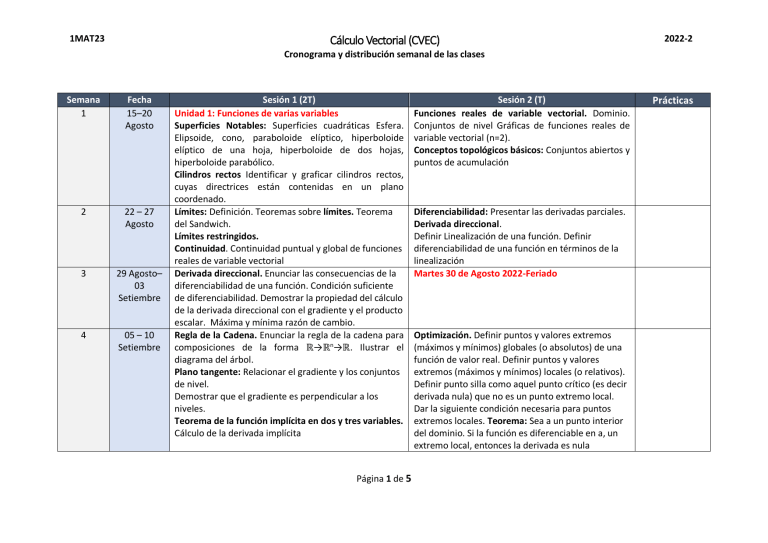
1MAT23 Cálculo Vectorial (CVEC) 2022-2 Cronograma y distribución semanal de las clases Semana 1 Fecha 15–20 Agosto 2 22 – 27 Agosto 3 29 Agosto– 03 Setiembre 4 05 – 10 Setiembre Sesión 1 (2T) Unidad 1: Funciones de varias variables Superficies Notables: Superficies cuadráticas Esfera. Elipsoide, cono, paraboloide elíptico, hiperboloide elíptico de una hoja, hiperboloide de dos hojas, hiperboloide parabólico. Cilindros rectos Identificar y graficar cilindros rectos, cuyas directrices están contenidas en un plano coordenado. Límites: Definición. Teoremas sobre límites. Teorema del Sandwich. Límites restringidos. Continuidad. Continuidad puntual y global de funciones reales de variable vectorial Derivada direccional. Enunciar las consecuencias de la diferenciabilidad de una función. Condición suficiente de diferenciabilidad. Demostrar la propiedad del cálculo de la derivada direccional con el gradiente y el producto escalar. Máxima y mínima razón de cambio. Regla de la Cadena. Enunciar la regla de la cadena para composiciones de la forma ℝ→ℝn→ℝ. Ilustrar el diagrama del árbol. Plano tangente: Relacionar el gradiente y los conjuntos de nivel. Demostrar que el gradiente es perpendicular a los niveles. Teorema de la función implícita en dos y tres variables. Cálculo de la derivada implícita Página 1 de 5 Sesión 2 (T) Funciones reales de variable vectorial. Dominio. Conjuntos de nivel Gráficas de funciones reales de variable vectorial (n=2). Conceptos topológicos básicos: Conjuntos abiertos y puntos de acumulación Diferenciabilidad: Presentar las derivadas parciales. Derivada direccional. Definir Linealización de una función. Definir diferenciabilidad de una función en términos de la linealización Martes 30 de Agosto 2022-Feriado Optimización. Definir puntos y valores extremos (máximos y mínimos) globales (o absolutos) de una función de valor real. Definir puntos y valores extremos (máximos y mínimos) locales (o relativos). Definir punto silla como aquel punto crítico (es decir derivada nula) que no es un punto extremo local. Dar la siguiente condición necesaria para puntos extremos locales. Teorema: Sea a un punto interior del dominio. Si la función es diferenciable en a, un extremo local, entonces la derivada es nula Prácticas 1MAT23 Cálculo Vectorial (CVEC) 2022-2 Cronograma y distribución semanal de las clases 5 6 12– 17 Setiembre 19 –24 Setiembre Derivadas parciales de orden superior: Definir derivadas parciales de orden superior y presentar su notación convencional. Teorema de Schwarz. Optimización local: Definir matriz Hessiana de una función. Dar condiciones suficientes acerca de la matriz Hessiana en un punto crítico para garantizar que sea un punto mínimo local, un punto máximo local o un punto silla.Criterio de la segunda derivada para extremos locales (dimensión2). Optimización global y Lagrange: Conjuntos cerrados y Funciones vectoriales de variable vectorial: de conjuntos acotados de espacios euclidianos. Enunciar Funciones vectoriales de variable vectorial: Funciones el Teorema de Weierstrass. componentes. Límite, continuidad y Optimización con restricciones: Definir puntos y valores diferenciabilidad. Definir matriz Jacobiana de una extremos de funciones reales restrictas a un conjunto. función diferenciable. Regla de la cadena .Regla del Enunciar el Teorema de Lagrange. Ejemplos de árbol. optimización global en dimensión 2 y optimización global en dimensión 3. Unidad 2: Integrales dobles y triples Cambio de variable: Enunciar el teorema de cambio Integrales dobles. Definición de la integral doble de una de variables. En particular describir los casos: lineal, función sobre un rectángulo usando sumas de Riemann. polares y polares modificadas. Interpretar geométricamente la integral doble como Aplicaciones: Desarrollar ejemplos de aplicación de volumen de un sólido de base rectangular. Enunciar el las integrales dobles: Cálculo de área, masa, centro de teorema de Fubini en rectángulos. Integrales dobles masa de láminas planas y volumen de sólidos. sobre regiones acotadas. Definir regiones tipo I y Ejemplo de momento de inercia regiones tipo II. Propiedades de las integrales: Linealidad respecto al integrando, aditividad respecto a la región, preservación del orden, simetría. Enunciar el teorema de Fubini para funciones continuas sobre regiones tipos I y II Página 2 de 5 PC1 Jueves 15 Setiembre (hasta Optimización local) 1MAT23 Cálculo Vectorial (CVEC) 2022-2 Cronograma y distribución semanal de las clases 7 26 Noviembre– 01 Octubre Integrales triples: Integrales triples sobre paralelepípedos: Dar la idea de la definición de la integral triple en paralelepípedos de una función, usando sumas de Riemann. Enunciar el teorema de Fubini para funciones continuas, definidas sobre sólidos proyectables sobre los planos coordenados planos coordenado. Cambio de variable, cilíndricas. Enunciar el teorema de cambio de variables para integrales triples. Cambios de coordenadas Cilíndrica. Cambios de coordenadas esféricas. Aplicaciones: Desarrollar ejemplos de aplicación de las integrales dobles: Cálculo de área, masa, centro de masa de láminas planas y volumen de sólidos. 8 03–08 Octubre Curvas: Funciones vectoriales de variable real: Definir funciones coordenadas de una función vectorial de variable real. Límite. Definir límite de una función vectorial de variable real en términos de sus funciones coordenadas. Continuidad. Definir continuidad puntual y global de una función vectorial de variable real. Curvas: Definir curva como la imagen de una función continua F∶𝐼→ ℝn , definida en un intervalo 𝐼. Curvas cerradas (simples y con nudos), orientación de curvas, yuxtaposición de curvas. Sábado 8 de Octubre 2022-Feriado 9 10–15 Octubre Examen Parcial 10 17– 22 Octubre Jueves 13 de Octubre Unidad 3: Integral de línea Curvas regulares. Longitud de arco: Campos escalares. Campo escalar. Dar la noción de conjuntos de nivel de un campo escalar. Página 3 de 5 PC2 Jueves 29 Setiembre (hasta Integral Doble) 1MAT23 Cálculo Vectorial (CVEC) Cronograma y distribución semanal de las clases 11 24 –29 Octubre Diferenciabilidad. Definir diferenciabilidad puntual y global de una función vectorial de variable real. Recta tangente a una curva: Interpretar geométricamente el vector tangente a una curva. Curvas regulares: Definir parametrización regular de una curva como aquella parametrización F∶𝐼→ ℝn , cuya derivada es no nula y continua en el conjunto de los puntos interiores de 𝐼. Definir curva regular como aquella curva que posee una parametrización regular. Longitud de arco. Definir longitud de arco de una curva. Deducir la forma del diferencial de longitud de arco. Definir función longitud de arco a partir de una parametrización de clase 𝐶1.Es decir, sea 𝛼: [𝑎, 𝑏] → 𝑅3 una parametrización de clase 𝐶1: 𝑡 𝑠(𝑡) = ∫𝑎 ‖𝛼´(𝑢)‖𝑑𝑢. Campos vectoriales. Campo vectorial. Definición de campo gradiente y función potencial, hay que enfatizar que los campos gradientes son ortogonales a los conjuntos de niveles (regulares) del potencial. Integral de línea de un campo vectorial. Propiedades. Aplicaciones: Trabajo. Principio de trabajo y energía Página 4 de 5 Integral de línea de un campo escalar. Propiedades. Aplicaciones: Masa y centro de masa de un alambre Teoremas Fundamentales para integrales de línea. Segundo Teorema Fundamental para integrales de línea. Conjuntos abiertos y conexos (abierto y conexo por caminos). Primer Teorema Fundamental para integrales de línea. 2022-2 1MAT23 Cálculo Vectorial (CVEC) 2022-2 Cronograma y distribución semanal de las clases 12 31 Octubre–05 Noviembre Condiciones necesarias y suficientes para que un campo vectorial sea un gradiente. Conjuntos simplemente conexos (considere que son conexos) Condiciones necesarias y suficientes para que un campo vectorial sea un gradiente. Cálculo de funciones potenciales. Martes 1 Noviembre 2022-Feriado Unidad 4: Integral de superficie Superficies. Superficies. Parametrización de superficies. Curvas coordenadas. Vector normal. Parametrización Regular y Superficie regular. Espacio tangente, orientación (vector normal unitario). Área de una superficie. Casos particulares. Integral de superficie de un campo vectorial. Integral de superficie de un campo vectorial. Propiedades. Aplicaciones: fluctuación de un campo vectorial a través de una superficie. 13 07 –12 Noviembre Teorema de Green. Teorema de la invariancia Calcular áreas de una región plana con borde regular usando el teorema de Green. 14 14–19 Noviembre Integral de superficie de un campo escalar. Integral de superficie de un campo escalar. Propiedades e interpretación. Aplicaciones: Masa y centro de masa de una lámina en R3 . 15 21 –26 Noviembre Rotacional: propiedades y caracterización de un campo gradiente mediante el rotacional. Teorema de Stokes (con borde conexo y no conexo) La orientación del borde inducida por la orientación de la superficie será llamada orientación inducida. Página 5 de 5 PC3 Jueves 3 de Noviembre (hasta Teoremas Fundamentales para integrales de línea) Divergencia: propiedades y caracterización de campo rotacionales mediante la divergencia. Teorema de Gauss (con borde conexo y no conexo). PC4 Jueves 17 de Noviembre (hasta Integral de superficie de un campo escalar) 1MAT23 Cálculo Vectorial (CVEC) Cronograma y distribución semanal de las clases 16 17 28 Noviembre– 03 Diciembre Jueves 1 de Diciembre 05 – 10 Diciembre Examen Especial Examen Final Página 6 de 5 2022-2