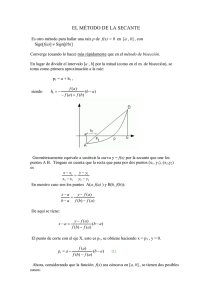
Investigación de Método de bisección También llamado dicotomía, es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz. Este es uno de los métodos más sencillos y de fácil intuición para resolver ecuaciones de una variable, también conocido como Método de Intervalo Medio. Se basa en el teorema del valor intermedio, el cual establece que toda función continua f en un intervalo cerrado [a,b] toma todos los valores que se hallan entre f (a) y f (b). Esto es que todo valor entre f (a) y f (b) es la imagen de al menos un valor en el intervalo [a, b]. En caso de que f (a) y f (b) tengan signos opuestos, el valor cero sería un valor intermedio entre f (a) y f (b), por lo que con certeza existe un p E [a, b] que cumple f (p) = 0 De esta forma, se asegura la existencia de al menos una solución de la ecuación f (x)=0. El método consiste en lo siguiente: Debe existir seguridad sobre la continuidad de la función f en el intervalo [a, b] A continuación, se verifica que f (a). f (b) < 0 Se calcula el punto m del intervalo [a, b] y se evalúa f (m) si ese valor es igual a cero, ya hemos encontrado la raíz buscada En caso de que no lo sea, verificamos si f (m) tiene signo opuesto con f (a) o con f (b) Se redefine el intervalo [a, b] como [a, m] o [m, b] según se haya determinado en cuál de estos intervalos ocurre un cambio de signo Con este nuevo intervalo se continúa sucesivamente encerrando la solución en un intervalo cada vez más pequeño, hasta alcanzar la precisión deseada Ejemplo: f (x) = x3 + 4x2 – 10 = 0 Interacción 1 Interacción 2 Grafica La tabla resume los valores de las iteraciones Tabla para bisección i 1 2 3 a c 1 1.5 1 1,25 1.25 … b f (a) f (c) f (b) tramo 2 1,5 1,5 -5 -5 2.37 -1.794 14 2.37 1 0.5 Método de la secante En análisis numérico el método de la secante es un método para encontrar los ceros de una función de forma iterativa. Es una variación del método de Newton-Raphson donde en vez de calcular la derivada de la función en el punto de estudio, teniendo en mente la definición de derivada, se aproxima la pendiente a la recta que une la función evaluada en el punto de estudio y en el punto de la iteración anterior. Este método es de especial interés cuando el coste computacional de derivar la función de estudio y evaluarla es demasiado elevado, por lo que el método de Newton no resulta atractivo. ¿Como es? El método se basa en obtener la ecuación de la recta que pasa por los puntos (xn−1, f (xn−1)) y (xn, f (xn)). A dicha recta se le llama secante por cortar la gráfica de la función. En la imagen de arriba a la derecha se toman los puntos iniciales x0 y x1, se construye una línea por los puntos (x0, f (x0)) y (x1, f (x1)). En forma punto-pendiente, esta línea tiene la ecuación mostrada anteriormente. Posteriormente se escoge como siguiente elemento de la relación de recurrencia, xn+1, la intersección de la recta secante con el eje de abscisas obteniendo la fórmula, y un nuevo valor. Seguimos este proceso, hasta llegar a un nivel suficientemente alto de precisión (una diferencia lo suficientemente pequeñas entre xn y xn-1). Ejemplo: Utilice el método de la secante para encontrar una raíz real de la ecuación polinomial: f (x)=x3+2x2+10x20=0. Utilizando la ecuación: Obtenemos: Y mediante x0=0 y x1=1 se calcula x2 Los valores posteriores son los siguientes: Grafica Xn | Xn + 1 – Xn | 0 0.00000 1 1.00000 1.00000 2 1.53846 0.53846 3 1.35031 0.18815 4 1.36792 0.01761 5 1.36881 0.00090 Ahí tenemos el resultado, cuando | Xn + 1 – Xn | < E =10-3 n Método de Jacobi Es un método iterativo, usado para resolver sistemas de ecuaciones lineales del tipo Ax = b El algoritmo toma su nombre del matemático alemán Carl Gustav Jakob Jacobi. El método de Jacobi consiste en usar fórmulas como iteración de punto fijo. Descripción La base del método consiste en construir una sucesión convergente definida iterativamente. El límite de esta sucesión es precisamente la solución del sistema. A efectos prácticos si el algoritmo se detiene después de un número finito de pasos se llega a una aproximación al valor de x de la solución del sistema. La sucesión se construye descomponiendo la matriz del sistema A en la forma siguiente: donde D, es una matriz diagonal y R, es la suma de una matriz triangular inferior L y una matriz triangular superior U, luego R = L + U. Partiendo de Ax = b, podemos reescribir dicha ecuación como: Luego, Si aii ≠ 0 para cada i. Por la regla iterativa, la definición del Método de Jacobi puede ser expresado de la forma: donde K es el contador de iteración, Finalmente tenemos: Ejemplo Un sistema lineal de la forma Ax=b con una estimación inicial x (0) está dado por: Usamos la ecuación x (k-1) = D-1 (b – Rx (k)) descrita anteriormente, para estimar x. Primero, reescribimos la ecuación de una manera más conveniente D-1 (b – Rx (k)) = Tx(k) + C, donde T= -D-1 R y C = D-1 b. vea que R=L+U donde L y U son las partes inferior y superior de A de los valores conocidos. Determinamos T= -D-1 (L + U) como C es encontrada como con T y C calculadas, estimaremos x como x (1) = Tx (0) + C siguientes iteraciones este proceso se repetirá hasta que converja (i.e., hasta que ||Ax(n)-b|| sea pequeño). la solución después de 25 iteraciones es: Aurys Brango De Meza