FUNCIONES

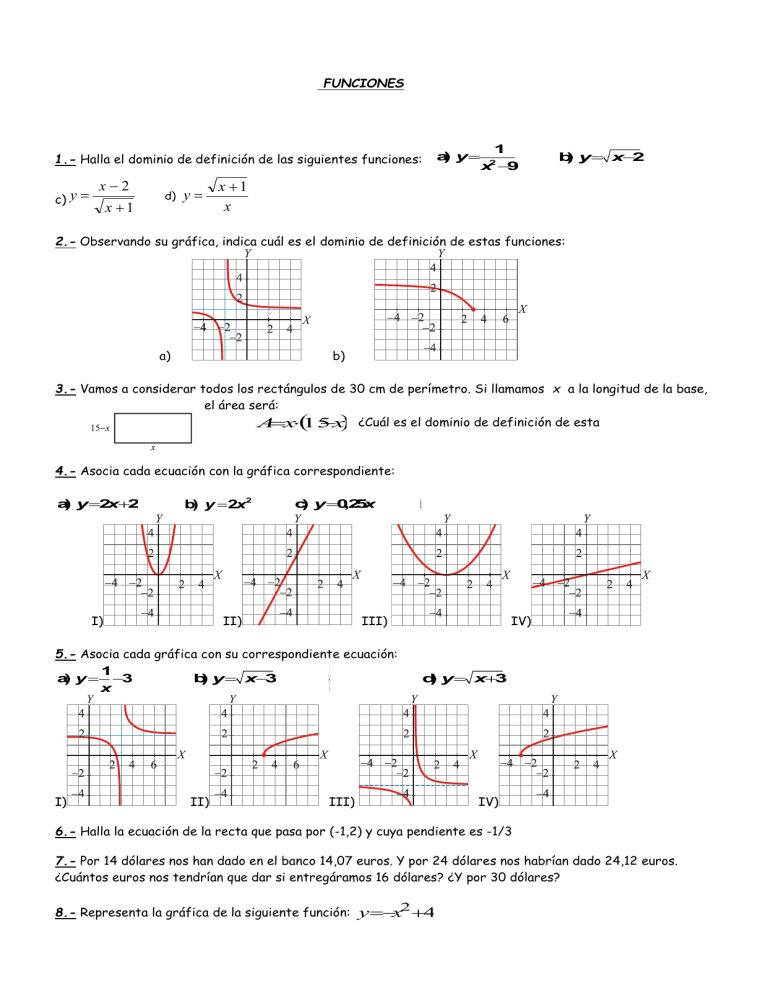
FUNCIONES
1.- Halla el dominio de definición de las siguientes funciones:
c) y 
x2
x 1
d)
y
a) y
1
x 9
2
b) y x2
x 1
x
2.- Observando su gráfica, indica cuál es el dominio de definición de estas funciones:
a)
b)
3.- Vamos a considerar todos los rectángulos de 30 cm de perímetro. Si llamamos x a la longitud de la base,
el área será:
Ax15
x ¿Cuál es el dominio de definición de esta
función?
4.- Asocia cada ecuación con la gráfica correspondiente:
a) y 2x2
b) y  2x2
I)
c) y 0,25x
II)
III)
5.- Asocia cada gráfica con su correspondiente ecuación:
1
1
c)y2
b) y x3
a) y  3
x3
x
I)
II)
d)y0,25x2
IV)
d) y x3
III)
IV)
6.- Halla la ecuación de la recta que pasa por (-1,2) y cuya pendiente es -1/3
7.- Por 14 dólares nos han dado en el banco 14,07 euros. Y por 24 dólares nos habrían dado 24,12 euros.
¿Cuántos euros nos tendrían que dar si entregáramos 16 dólares? ¿Y por 30 dólares?
8.- Representa la gráfica de la siguiente función:
y x2 4
 x 2  1 si x  2
y
9.- Representa gráficamente la siguiente función:
en los otros casos
3
10.- Un cántaro vacío con capacidad para 20 litros pesa 2550 gramos. Escribe la función que nos da el peso
total, en kilos, del cántaro según la cantidad de agua, en litros, que contiene.
11.- A partir de la gráfica de
a) y = f (x) - 2 b) y= -f (x)
y  f (x) construye las gráficas de
a)
12.- Sabiendo que la gráfica de
b)
y  f (x) es la de la izquierda, representa la gráfica de y  f (x)
13.- Expresa como función "a trozos":
y
y
14.- Representa las funciones:
x 1
2
x 1  2
3x2
b) y
x1
f(x)2x21 y g(x)  x , calcula:
( f g )( x)
(g f)(x)
2x  1
x 1
Dadas las funciones f ( x ) 
y . g ( x) 
Calcula ( f
x 1
x2
15.- Dadas las funciones
g )( x)
(g f)(x)
¿Qué relación hay entre f(x) y g(x)?
16.- Dada la gráfica de la función y = f(x):
Calcula f-1(0)
f-1(1)
 x4
si
x  2
 x
 x  1
si  2  x  2
17- .- Estudia la continuidad de las siguientes funciones n( x)  
 x3
 x  1 si
2 x
 2 x  1
 x 2  4

 2 x  3
p( x)   5
 x
 x4

si
2 x
si  2  x  0
si
0 x5
si
5 x
x3
si x  1


18.- Dada la función f(x) = 
mx  n
si 1  x  3 , halla los valores de m y n para que f(x) sea continua
 x 2  10x  11 si x  3

19.- Calcula los siguientes límites:
 5x 2  2 x  1 

a) lim 
4 x  2 
x  
c)
1
x
lim
lim Ln x  1
d)
lim 
x 1
x3 2
f)
x2
e) lim
x 1
x 2
 3x 2
3x 3 
lim 
 2 
x x  1
x 1

x3  8
x2  4
b)
x  x3
x

x3
x 3 x  5 x 2  3 x  9
lim
3
lim
x 2
3x  6
( x  2)
2
3x 3
y di razonadamente cómo se sitúa la curva con respecto a
x2 1
20- Calcula las asíntotas de la función y 
ellas.
21.- Estudia la continuidad de la siguiente función y, si hay discontinuidad, indica que qué tipo es.
 5x  3

f ( x)   2 x  1
x

 2 2
six  0
six  0
1
aplicando la definición en el punto de abscisa 3.
2x  4
23.- Calcula, aplicando la definición, el valor de la derivada de y  x  1 , en el punto de abscisa “a”.
22.- Calcula el valor de la derivada de
y
Deriva y simplifica si se puede.
1.-
y7
x2
4x 2  9
x 2  25
2
2
7.- y  5 x  3 4 x
3
2x  1
10.- y 
7
4.- y 
2.- y  Ln 
5.-
y  e5x
3
5x  3
2  3x

x
8.- y  log 2 (7 x  2)
3
x2 1
x
2
6.- y  cos(5 x  )
3
2
5 x
9.- y 
senx
3.- f ( x ) 
.- Dada la función f ( x)  1  x  x , calcula la ecuación de recta tangente a la curva en x=2.
2