optimización

RESUMEN DE CÁLCULO III
INGENIERÍA CIVIL 10129
COORDINADOR: M. BRAVO
UNIVERSIDAD DE SANTIAGO DE CHILE
FACULTAD DE CIENCIA
DEPARTAMENTO DE MATEMÁTICA Y C. C.
Optimización
1. Recuerdo del caso de funciones de una variable
En esta sección recordaremos los aspectos básicos relacionados a extremos de una función
de una variable. Esto nos permitirá una analogı́a con el caso de varias variables.
Definición 1. Sea h : [a, b] → R una función tal que sus derivadas h0 y h00 existen en todo
su dominio.
(a) La función h tiene un máximo local en x0 si existe una vecindad V de x0 tal que
h(x0 ) ≥ h(x) para todo x ∈ V.
(b) La función h tiene un mı́nimo local en x0 si existe una vecindad V de x0 tal que
h(x0 ) ≤ h(x) para todo x ∈ V.
(c) El punto x0 ∈ [a, b] es un punto crı́tico de h si satisface que h0 (x0 ) = 0.
Proposición 1. Si h tiene un máximo o mı́nimo local en x0 , entonces h0 (x0 ) = 0. Es decir,
x0 es un punto crı́tico de h.
Recordemos que, en el caso de una variable, la expansión de Taylor de segundo orden de
h alrededor del valor crı́tico x0 es:
1
h(x) − h(x0 ) = h0 (x0 )(x − x0 ) + h00 (x0 )(x − x0 )2 + |x − x0 |2 R2 (x0 , x)
| {z }
2
=0
donde R2 (x0 , x) → 0, cuando x → x0 .
Intuitivamente, como el resto R2 (x0 , x) es pequeño, el signo de h(x) − h(x0 ) depende
exclusivamente del signo de h00 (x0 ).
Ahora, el criterio de la segunda derivada aplica cuando h00 es continua en x0 . En este caso
tenemos:
Proposición 2. Sea h una función tal que h00 es continua en una vecindad de x0 con h0 (x0 ) =
0. Entonces
(a) Si h00 (x0 ) > 0, entonces h tiene un mı́nimo local en x0 .
(b) Si h00 (x0 ) < 0, entonces h tiene un máximo local en x0 .
2. Extremos de funciones para funciones de varias variables
De la misma manera que en el caso de una variable real, es posible definir los conceptos de
máximo local, mı́nimo local, extremo local y punto crı́tico para una función f : D ⊆ Rn → R,
donde supondremos D abierto para facilitar las hipótesis.
Definición 2. Sea f : D ⊆ Rn → R.
(a) La función f alcanza un máximo local en ~x0 si existe una vecindad V de ~x0 tal que
f (~x0 ) ≥ f (~x), para todo ~x ∈ V.
1
2
(b) La función f alcanza un mı́nimo local en ~x0 si existe una vecindad V de ~x0 tal que
f (~x0 ) ≤ f (~x), para todo ~x ∈ V.
(c) Se dice que la función f alcanza un extremo local en ~x0 si es o bien un mı́nimo local
o bien un máximo local en ~x0 .
(d) Se dice que la función f tiene un punto crı́tico en ~x0 si ∇f (~x0 ) = ~0.
(e) La función f tiene un punto silla en ~x0 ∈ D si ~x0 es un punto crı́tico pero no es un
extremo local de f .
Observación 1. Notemos que la igualdad ∇f (~x0 ) = ~0 es un sistema de n ecuaciones y n
incógnitas:
∂f
∂f
∂f
(~x0 ) = 0,
(~x0 ) = 0, . . . ,
(~x0 ) = 0.
∂x1
∂x2
∂xn
El siguiente resultado es el análogo al caso de varias variables de la Proposición 1.
Proposición 3. Sea f : D ⊆ Rn → R una función diferenciable. Si ~x0 ∈ D es un extremo
local de f entonces ∇f (~x0 ) = ~0.
Observación 2. Análogamente al caso real, la Propiedad 3 implica que, si se quiere buscar
un extremo local de una función diferenciable en un abierto D, los únicos candidatos posibles
son las soluciones de ∇f (~x) = ~0.
Ahora es necesario estudiar una condición de segundo orden para clasificar un punto crı́tico
para una función f : D ⊆ Rn → R que sea análoga al caso de una variable donde se estudia el
signo de h00 (x0 ). Esta noción involucra el estudio de la matriz Hessiana de f : D ⊆ Rn → R.
Recordemos que el Hessiano de f en un punto ~x0 ∈ D está dado por
∂2f
x0 )
2 (~
 ∂x1
 ∂2f
 ∂x2 ∂x1 (~x0 )


Hf (~x0 ) = 


..
.
∂2f
x0 )
∂xn ∂x1 (~
∂2f
x0 )
∂x1 ∂x2 (~
∂2f
x0 )
∂x1 ∂x3 (~
···
∂2f
(~x0 )
∂x22
∂2f
x0 )
∂x2 ∂x3 (~
···
∂2f
x0 )
∂xn ∂x2 (~
..
∂2f
∂2f
x0 )
∂x1 ∂xn (~


∂ 2 f (~
x0 )
x0 )
∂x2 ∂xn (~


..
.
.
x0 )
∂xn ∂x3 (~
···
∂2f
(~x0 )
∂x2n
n
n
∈R ×R .


El Hessiano de f en ~x0 tiene asociado una forma cuadrática asociada dada explı́citamente
por
Hf (~x0 )(~v ) =
n
1 X ∂2f
1
(~x0 )vi vj = ~v T Hf (~x0 )~v ,
2
∂xi ∂xj
2
~v ∈ Rn .
i,j=1
Recordemos el resultado siguiente, que dice que si la función f es suficientemente regular
en ~x0 , entonces las derivadas parciales cruzadas deben ser iguales.
3
Teorema 1 (Teorema de Schwarz). Sea f : D ⊆ Rn → Rn una función de clase1 C 2 en el
abierto D con x0 ∈ D. Entonces
∂2f
∂2f
(x0 ) =
(x0 )
∂xi ∂xj
∂xj ∂xi
∀ i, j = 1, ..., n
Observación 3. Notemos que por el Teorema de Schwarz, si f es de clase C 2 en una vecindad
de x0 , entonces la matriz Hessiana Hf (~x0 ) es simétrica.
Como en el caso real, para una función escalar f : D ⊆ Rn → R suficientemente regular es
posible obtener una expansión de Taylor de segundo orden en el punto ~x0 .
Teorema 2 (Teorema de Taylor de 2o orden). Sea f : D ⊆ Rn → R una función de clase C 2
en una bola abierta B ⊆ D que contiene a ~x0 . Para todo ~x ∈ B, se cumple
1
f (~x) − f (~x0 ) = h∇f (~x0 ), ~x − ~x0 i + (~x − ~x0 )T Hf (~x0 )(~x − ~x0 ) + k~x − ~x0 k2 R2 (~x0 , ~x)
2
tal que R2 (~x0 , ~x) → 0 cuando ~x → ~x0 ,
Observación 4. Notemos que, cuando ~x0 es un punto crı́tico de f , esto es, ∇f (~x0 ) = 0 se
tiene que h∇f (~x0 ), ~x − ~x0 i = 0. Ası́,
1
f (~x) − f (~x0 ) = (~x − ~x0 )T Hf (~x0 )(~x − ~x0 ) + k~x − ~x0 k2 R2 (~x0 , ~x).
2
Por tanto, intuitivamente, como el resto R2 (~x0 , ~x) es pequeño se tiene que el signo de f (~x) −
f (~x0 ) depende exclusivamente de la forma cuadrática (~x − ~x0 )T Hf (~x0 )(~x − ~x0 ) para todo
vector ~x ∈ Rn cercano a ~x0 .
Motivados por la observación anterior, tenemos la siguiente definición.
Definición 3. Sea A una matriz de dimensión n × n. La matriz A se dice
(a) Definida positiva cuando la forma cuadrática ~xT A~x satisface ~xT A~x > 0 para todo
~x 6= ~0.
(b) Definida negativa cuando la forma cuadrática ~xT A~x satisface ~xT A~x < 0 para todo
~x 6= ~0.
(c) Semidefinida positiva cuando la forma cuadrática ~xT A~x satisface ~xT A~x ≥ 0 para todo
~x ∈ Rn .
(d) Semidefinida negativa cuando la forma cuadrática ~xT A~x satisface ~xT A~x ≤ 0 para
todo ~x ∈ Rn .
1Recuerde que una función es de clase C 2 en un punto ~
x si es dos veces diferenciable con segundas derivadas
continuas en ~
x.
4
Observación 5. Recuerde de su curso de Álgebra Lineal que una matriz A ∈ Rn×n se dice
diagonalizable si existe una matriz P tal que
A = P DP T ,
donde P es una matriz invertible (ortogonal) y D es

λ1

 0

PTP = I
y
D= .
 ..

0
una matriz diagonal, es decir,

0 ··· 0

λ2 · · · 0 

.
.. . .
.. 
. . 
.

0 · · · λn
Los reales λ1 , λ2 , . . . , λn son los valores propios de A.
Recuerde además que si A es una matriz simétrica a valores reales, entonces A es diagonalizable y todos sus valores propios están en R.
Un resultado útil que permite saber si una matriz A ∈ Rn×n es definida (o semidefinida)
positiva o definida (o semidefinida) negativa se enuncia más abajo.
Proposición 4. Sea A una matriz a valores reales de dimensión n × n. Luego
(a) A es definida positiva si y sólo si A tiene valores propios estrictamente positivos.
(b) A es definida negativa si y sólo si A tiene valores propios estrictamente negativos.
(c) A es semidefinida positiva si y sólo si A tiene valores propios positivos.
(d) A es semidefinida negativa si y sólo si A tiene valores propios negativos.
Observación 6. Es necesario notar que el cálculo de los valores propios de una matriz
puede ser complicado. Como el Hessiano de una función de clase C 2 es una matriz simétrica
podemos acudir a un resultado más especı́fico y mucho más simple de usar.
Un criterio para determinar si una matriz simétrica A es definida positiva o definida negativa es el siguiente.
Proposición 5. Sea A = (aij ) una matriz simétrica de dimensión n × n y sea Ar = (aij )
la matriz cuadrada de dimensión r × r cuya primera entrada es a11 , para todo r = 1, . . . , n.
Entonces A es
(a) Definida positiva si det(Ar ) > 0, para todo r = 1, . . . , n.
(b) Definida negativa si (−1)r det(Ar ) > 0, para todo r = 1, . . . , n. Es decir, det(A1 ) < 0,
det(A2 ) > 0, . . .
(c) Semidefinida positiva si det(Ar ) ≥ 0, para todo r = 1, . . . , n.
(d) Semidefinida negativa si (−1)r det(Ar ) ≥ 0, para todo r = 1, . . . , n. Es decir, det(A1 ) ≤
0, det(A2 ) ≥ 0, . . .
5
En palabras sencillas si los determinantes de las submatrices superiores son todos estrictamente positivos, entonces la matriz es definida positiva. En cambio si son de signo alternante,
partiendo de negativo, se trata de una matriz definida negativa. Veamos un ejemplo.
Ejemplo 1. Sea f : R3 → R, dada por f (x, y, z) = y − 4x2 + 3xy − y 2 − z 2 . Probemos que
la mztriz Hessiana de f es definida negativa en todo punto de R3 .
Como f es una función de clase C 2 , el Hessiano es simétrico y podemos aplicar el criterio
dado por la Proposición 5. Ahora, los determinantes de las submatrices del Hessiano para
una función de 3 variables son:
det(H1 ) =
∂ 2 f (~x)
, det(H2 ) =
∂x21
∂2f
(~x)
∂x2
∂2f
x)
∂x∂y (~
∂2f
x)
∂x∂y (~
∂2f
(~x)
∂y 2
, det(H3 ) =
∂2f
(~x)
∂x2
2
∂ f
x)
∂x∂y (~
∂2f
x)
∂x∂z (~
∂2f
x)
∂x∂y (~
2
∂ f
(~x)
∂y 2
∂2f
x)
∂y∂z (~
∂2f
x)
∂x∂z (~
2
∂ f
x)
∂y∂z (~
∂2f
(~x)
∂z 2
donde ~x = (x, y, z). Ahora, calculando las derivadas tenemos que
∂f
(~x) = −8x + 3y,
∂x
∂2f
(~x) = −8,
∂x2
∂2f
(~x) = 3,
∂y∂x
∂2f
(~x) = 0,
∂z∂x
∂f
(~x) = 1 + 3x − 2y,
∂y
∂2f
(~x) = −2,
∂y 2
∂2f
(~x) = 3,
∂x∂y
∂2f
(~x) = 0,
∂z∂y
∂f
(~x) = −2z,
∂z
∂2f
(~x) = −2,
∂z 2
∂2f
(~x) = 0,
∂x∂z
∂2f
(~x) = 0.
∂y∂z
Por lo tanto, la matriz Hessiana es constante para todos los puntos (se trata de una función
cuadrática). Luego, tenemos que
det(H1 ) = −8 < 0,
det(H2 ) =
det(H3 ) =
−8
3
3
−2
−8
3
0
3
−2
0
0
0
−2
= 16 − 9 = 7 > 0,
= −2 · 7 = −14 < 0.
Los signos de las submatrices de la matriz Hessiana son alternados, con |H1 | negativo. En
conclusión la matriz Hessiana es definida negativa en todo punto de R3 .
Ahora podemos establecer los resultados necesarios para la clasificiación de puntos crı́ticos
de la función f .
El primer resultado contiene condiciones necesarias para máximos y mı́nimos locales.
Teorema 3 (Condiciones necesarias de 2o orden). Sea f : D ⊆ Rn → R de clase C 2 en un
abierto D. Sea ~x0 un punto crı́tico de f . Entonces
(a) Si f alcanza un mı́nimo local en ~x0 , entonces Hf (~x0 ) es semidefinida positiva.
,
6
(b) Si f alcanza un máximo local en ~x0 , entonces Hf (~x0 ) es semidefinida negativa.
El siguiente es un resultado de suficiencia para la clasificación de puntos crı́ticos.
Teorema 4 (Condiciones suficientes de 2o orden). Sea f : D ⊆ Rn → R de clase C 2 en un
abierto D. Sea ~x0 un punto crtı́tico de f . Entonces
(a) Si Hf (~x0 ) es definida positiva, entonces f alcanza un mı́nimo local en ~x0 .
(b) Si Hf (~x0 ) es definida negativa, entonces f alcanza un máximo local en ~x0 .
(c) Si Hf (~x0 ) no es definida positiva ni definida negativa, entonces f tiene un punto silla
en ~x0 .
Observación 7. Para notar la diferencia entre los dos resultados anteriores tomemos la
función f (x, y) = x4 + y 2 que claramente tiene a (0, 0) como único punto crı́tico. Un cálculo
sencillo muestra que la matriz Hessiana en (x, y) es
!
4x3 0
=⇒ Hf (0, 0) =
Hf (x, y) =
0 2
0 0
!
.
0 2
La matriz Hf (0, 0) es semidefinida positiva y entonces NO se puede concluir que es un mı́nimo
local USANDO el Teorema 4. Sin embargo, es fácil ver que f (x, y) ≥ 0 para todo (x, y) y
entonces (0, 0) es, de hecho, un mı́nimo global de f . Ahora, la condición necesaria dada
por el Teorema 3 nos dice simplemente que Hf (0, 0) es semidefinida positiva (cosa que ya
sabı́amos).
Ejemplo 2. Encontrar todos los puntos crı́ticos de f (x, y) = x2 + xy + y 2 − 3x y clasificarlos.
Primero es necesario encontrar los puntos crı́ticos de f , resolviendo la ecuación ∇f = ~0,
es decir,
∂f
∂f
= 2x + y − 3,
= x + 2y.
∂x
∂y
Se debe resolver entonces el sistema de ecuaciones 2x + y − 3 = 0, x + 2y = 0. La única
solución del sistema es el punto (x, y) = (2, −1), siendo luego el único punto crı́tico. La
matriz Hessiana de f en el punto (2, 1) es
Hf (2, −1) =
2 1
!
1 2
Como det(H1 ) = 2 y det(H2 ) = 3, se conlcuye que f alcanza un mı́nimo local en el punto
(2, −1).
Ejemplo 3. Encontrar todos los puntos crı́ticos de f (x, y) = 2x3 + 6xy + 3y 2 y clasificarlos.
Imponiendo que ∇f = ~0, se tiene
∂f
= 6x2 + 6y,
∂x
∂f
= 6x + 6y.
∂y
7
Luego, resuelve el sistema 6x2 + 6y = 0, 6x + 6y = 0. Las soluciones son (x1 , y1 ) =
(1, −1), (x2 , y2 ) = (0, 0). La matriz Hessiana de f en (x, y) está dada por
Hf (x, y) =
12x
6
6
12
!
.
Luego.
Hf (1, −1) =
12
6
6
12
!
Hf (0, −0) =
,
0
6
!
6 12
(a) En el caso del punto (1, −1), los determinantes son det(H1 ) = 12 y det(H2 ) = 108,
por lo que f alcanza un mı́nimo local en (1, −1).
(b) En el caso del punto (0, 0), como det(H1 ) = 0 y det(H2 ) = −26, tenemos que (0, 0)
es un punto silla de f .
3. Extremos de funciones con restricciones de igualdad: Método de los
multiplicadores de Lagrange
En este capı́tulo estamos interesados en problemas de optimización con restricciones de
igualdad, es decir, problemas del tipo minimización (o maximización) siguiente
min f (~x)
(ó
max f (~x))
(P)
s.a.
gi (~x) = 0,
i = 1, . . . , m,
donde f, g1 , . . . , gm : D ⊆ Rn → R, con m < n.
También podemos representar el sistema de ecuaciones dado por las restricciones como
G(~x) = ~0, donde G : D ⊆ Rn → Rm definida como G(~x) = (g1 (~x), . . . , gm (~x)).
Para este tipo de problemas, el método de los multiplicadores de Lagrange proporciona
condiciones necesarias que deben cumplirse en el óptimo, es decir, condiciones de primer
orden. La idea es convertir el problema en otro sin restricciones ampliado en m variables λi ,
que llamaremos multiplicadores de Lagrange, tal que la solución de este sistema ampliado,
(~x, ~λ), coincida en las variables ~x con la solución del problema original (P ), y cumpla las
restricciones gi (~x) = 0, para todo i ∈ {1, . . . , m}.
Definición 4 (Conjunto factible). El conjunto factible S ⊆ Rn del problema (P ) es el conjunto de puntos de Rn que satisface las restricciones del problema, es decir,
S = {~x = (x1 , . . . , xn ) ∈ D : gi (x1 , . . . , xn ) = 0, i = 1, . . . , m}
8
Definición 5 (hipótesis de calificación de las restricciones). Diremos que el punto ~x0 satisface
la hipótesis de calificación de las restricciones si el conjunto {∇g1 (~x0 ), . . . , ∇gm (~x0 )} es una
familia linealmente independiente de vectores.
Estudiemos primero el caso de una restricción.
Teorema 5 (Multiplicadores de Lagrange, una restricción). Sean f, g : D ⊆ Rn → R dos
funciones de clase C 1 . Consideremos el problema
min f (~x)
s.a.
(ó
max f (~x))
g(~x) = 0.
Sea ~x0 un extremo local de f en S. Supongamos que ∇g(~x0 ) 6= ~0, es decir, ~x0 satisface la
hipótesis de calificación. Entonces, existe λ ∈ R tal que
∇f (~x0 ) = λ∇g(~x0 ).
Teorema 6 (Multiplicadores de Lagrange, caso general). Sean f, g1 , . . . , gm : D ⊆ Rn → R
funciones de clase C 1 , con m < n. Sea ~x0 un extremo local de f en S que satisface la hipótesis
de clasificación. Entonces existen constantes λ1 , . . . , λm ∈ R tales que
∇f (~x0 ) =
(C)
m
X
λi ∇gi (~x0 ).
i=1
Observación 8. Las constantes λ1 , . . . , λm se llaman multiplicadores de Lagrange. La
función L : Rn × Rm → R definida por
L(x1 , . . . , xn , λ1 , . . . , λm ) = f (x1 , . . . , xn ) −
m
X
λi gi (x1 , . . . , xn ),
i=1
se conoce como Lagrangeano del problema. Observemos que

Pm
∂L
∂f
∂gi

~


 ∂xj (~x, λ) = ∂xj (~x) − i=1 λi ∂xj (~x), j = 1, . . . , n

∂L


(~x, ~λ) = gi (~x),
i = 1, . . . , m.

∂λi
Entonces, (~x0 , ~λ) ∈ Rn × Rm satisface (C) con ~x0 ∈ S si y sólo si es un punto crı́tico del
Lagrangeano, es decir, ∇L(~x0 , ~λ) = ~0.
Ejemplo 4. Encontrar los puntos de la curva C ⊆ R3 definida como la intersección entre
las superficies de ecuaciones
x2 − xy + y 2 − z 2 = 1,
y
que están a distancia máxima y mı́nima del origen.
x2 + y 2 = 1,
9
Solución: La distancia de un punto (x, y, z) al origen es
D(x, y, z) =
p
x2 + y 2 + z 2
Entonces, el Lagrangeano del problema es
L(x, y, z, λ1 , λ2 ) =
p
x2 + y 2 + z 2 − λ1 (x2 − xy + y 2 − z 2 − 1) − λ2 (x2 + y 2 − 1).
La ecuación ∇L = ~0 se escribe como
x
p
= λ1 (2x − y) + 2λ2 x,
x2 + y 2 + z 2
y
p
= λ1 (−x + 2y) + 2λ2 y,
2
x + y2 + z2
z
p
= −2λ1 z,
x2 + y 2 + z 2
x2 − xy + y 2 − z 2 − 1 = 0,
x2 + y 2 − 1 = 0.
Es claro que la curva no pasa por el origen, luego (x, y, z) 6= (0, 0, 0) para todo (x, y, z) ∈ C.
Multiplicando la primera ecuación por y, la segunda por x, luego restando, se obtiene que
λ1 (x2 − y 2 ) = 0. Las posibilidades son entonces λ1 = 0, x = y ó x = −y.
• Si λ1 = 0, entonces z = 0 y con ello, x2 − xy + y 2 = 1. De esta última ecuación y de
x2 + y 2 − 1 = 0, se obtiene que x = 0 ó y = 0. Si x = 0, entonces y = ±1 y λ2 = 1/2. Si
y = 0, entonces x = ±1 y otra vez λ2 = 1/2.
Resumiendo, obtenemos que los siguientes son puntos crı́ticos del Lagrangeano:
1
1
1
1
, −1, 0, 0, 0,
, 0, 1, 0, 0,
, 0, −1, 0, 0,
1, 0, 0, 0,
2
2
2
2
√
• Si se tiene qu x = y, entonces de la última ecuación del sistema se deduce x = ±
2
2 .
Para calcular el valor de z, ocupamos la ecuación x2 − xy + y 2 − z 2 − 1 = 0. Luego se tiene
que z 2 = −x2 y entonces x = z = 0, una contradicción.
• En el caso que x = −y, la última ecuación del sistema implica que x = ±
que de la penúltima, se deduce la igualdad
z2
=
x2 ,
√
2
2 ;
mientras
es decir z = ±x. Con estos valores, en
cada caso, se obtienen los multiplicadores de Lagrange λ1 , λ2 . De este análisis obtenemos los
puntos crı́ticos
√
√ √
√ ! √
√
√
√ !
2
2 2 −1
2
2
2
2 −1
2
,−
,
, √ ,−
,
,−
,−
, √ ,−
,
2
2 2
8
2
2
2
8
6
6
√ !
√ !
√ √ √
√ √
√
2 2 2 −1
2
2 2
2 −1
2
−
,
,
, √ ,−
, −
,
,−
, √ ,−
.
2 2 2
8
2 2
2
8
6
6
10
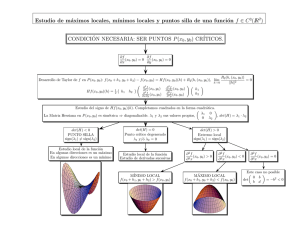
Figura 1. Intersección de las superficies x2 − xy + y 2 − z 2 = 1 y x2 + y 2 = 1.
Ahora bien, ¿Cómo saber cuál o cuáles puntos minimizan y maximizan la función
objetivo? No tenemos, en este caso, un criterio de segundo orden. Es necesario entonces
refinar el análisis. Notemos que la curva intersección es cerrada y acotada, es decir, compacta
(y tiene dos secciones separadas, Ver Figura 1). Primero, la curva es cerrada trivialmente.
Para ver que la curva es acotada, usamos que está contenida en el cilindro x2 + y 2 = 1 y, al
reemplazar en la ecuación de la primera superficie, se obtiene que z 2 = −xy. Como x e y son
acotados, z es acotado en C. Esto prueba que la figura es acotada.
Luego, usando el Teorema de Wierstrass y el hecho que la distancia es una función continua, sabemos que la distancia al origen tiene un máximo y un mı́nimo. Como hemos
detectado todos los posibles candidatos a puntos extremos del problema restringido basta
evaluar simplemente en los puntos que obtuvimos y comparar los valores. Luego,
D(1, 0, 0) = D(−1, 0, 0) = D(0, 1, 0) = D(0, −1, 0) = 1.
Por otro lado,
√ √ !
√
2
2 2
,−
,
=D
D
2
2 2
√
√
√ !
2
2
2
,−
,−
,
2
2
2
√ √ √ !
√ √
√ ! r
2 2 2
2 2
2
3
=D −
,
,
=D −
,
,−
=
> 1.
2 2 2
2 2
2
2
Entonces, los primeros cuatro puntos corresponden a mı́nimos de la distancia al origen de la
curva mientras los últimos cuatro son máximos.
11
Observación 9. El estudio de condiciones generales de segundo orden para extremos restringidos va más allá del objetivo de este resumen de curso. Luego, nos remitiremos principalmente al caso donde el conjunto es compacto y se puede hacer un razonamiento análogo
al del ejemplo.
El siguiente ejemplo muestra la importancia de verificar que el punto en estudio verifica
las condiciones de calificación.
Ejemplo 5. Se quiere encontrar el mı́nimo de la función f (x, y, z) = y + x2 z bajo las restricciones x6 − z = 0, y 3 − z = 0. ¿Cuál es el mı́nimo de la función? ¿Se puede usar el método
de los multiplicadores de Lagrange en este caso?
Solución: Las restricciones nos dicen que y ≥ 0 y z ≥ 0 y entonces f ≥ 0 para todo
(x, y, z) en el conjunto definido por las restricciones. Como (0, 0, 0) es factible, tiene que ser
el mı́nimo de f . (También se puede reemplazar directamente el valor de y, z en función de x
y escribir una función de una variable).
Ahora bien, definiendo g1 (x, y, z) = x6 − z y g2 (x, y, z) = y 3 − z, se ve que ∇g1 (0, 0, 0) =
∇h2 (0, 0, 0) = (0, 0, −1), es decir, no son linealmente independientes y el método de Lagrange
no entregará información. De hecho, ∇f (0, 0, 0) = (0, 1, 0) y entonces es imposible que existan
multiplicadores de Lagrange, dado que este vector no puede ser una combinación lineal entre
∇g1 (0, 0, 0) y ∇g2 (0, 0, 0).
4. Extremos de funciones con restricciones de igualdad y desigualdad:
Condiciones de Karush-Kuhn-Tucker (KKT)
En esta sección trataremos un caso más general de optimización que surge cuando aparecen
tanto restricciones de igualdad como de desigualdad. Nos interesa un problema del tipo
min f (~x)
(Q)
s.a.
gi (~x) = 0,
i = 1, . . . , m,
hi (~x) ≤ 0,
i = 1, . . . , `.
donde f, gi , hj : D ⊆ Rn → R son funciones de clase C 1 . Como antes, las funciones gi definen
restricciones de igualdad, mientras que las hj definen restricciones de desigualdad.
Observación 10. Notemos que en este caso sólo hablamos de un problema de minimización.
Para estudiar el problema de maximización, basta usar la relación
− min −f (x) = max f (x).
x∈C
x∈C
Observación 11. En un ligero abuso de notación, se suele decir que “gi es una restricción
de igualdad” y que “hj es una restricción de desigualdad”,
12
Definición 6 (Conjunto factible). El conjunto factible C ⊆ Rn del problema (Q) es el conjunto de puntos ~x ∈ Rn que satisfacen todas las restricciones del problema, esto es,
C = {~x ∈ D : gi (~x) = 0, ∀ i = 1, . . . , m ; hj (~x) ≤ 0, ∀ j = 1, . . . , `} ⊆ Rn .
A un punto de este conjunto lo llamaremos punto factible.
Definición 7 (Restricción activa). Diremos que una restricción de desigualdad hj está activa en el punto factible ~x0 si ésta se satisface con igualdad, esto es, si hj (~x0 ) = 0. Definiremos el conjunto de ı́ndices correspondientes a las restricciones activas en ~x0 por:
J(~x0 ) = {j ∈ {1, . . . , `} : hj (~x0 ) = 0}.
Intuitivamente, la idea en el desarrollo del criterio de Karush-Kuhn-Tucker (KKT) usa el
hecho que si una restricción de desigualdad, hj , está activa en el óptimo ~x0 , entonces puede
tratarse como una de igualdad asignándosele un multiplicador µj . Si no está activa entonces
puede ignorarse, con lo que su multiplicador µj debe ser cero. La condición que resume esta
discusión es simplemente que µj hj (~x0 ) = 0. Más aún el multiplicador asociado µj deberá ser
positivo.
Tal como en el caso con restricciones de igualdad, se necesita una condición de calificación
en el punto de estudio.
Definición 8 (hipótesis de calificación de las restricciones). Diremos que el punto ~x0 satisface
la hipótesis de calificación de las restricciones si el conjunto
{∇gi (~x0 ), ∇hj (~x0 ), i ∈ {1, . . . , m}, j ∈ J(~x0 )}
es linealmente independiente.
Observación 12. Note que el conjunto anterior considera solo aquellas restricciones de
desigualdad que están activas en ~x0 .
El siguiente teorema describe condiciones de primer orden para el problema (Q) y se
conoce como el criterio de Karush-Kuhn-Tucker (KKT). Permite, tal como en el caso sin
restricciones o con restricciones de igualdad, encontrar candidatos a óptimos (locales) del
problema de optimización en estudio.
Teorema 7 (KKT). Sean f : Rn → R, gi : Rn → R, i = 1, . . . , m y hj : Rn → R, j = 1, . . . , `
funciones de clase C 1 . Sea ~x0 un extremo del problema (Q) que satisface la hipótesis de
13
calificación. Entonces existen escalares λ1 , . . . , λm ∈ R y µ1 , . . . , µ` ∈ R tales que
∇f (~x0 ) +
[Optimalidad]
m
X
λi ∇gi (~x0 ) +
i=1
l
X
µj ∇hj (~x0 ) = ~0,
j=1
[Holgura Complementaria]
µi hi (~x0 ) = 0,
i = 1, . . . `
[Positividad]
µi ≥ 0,
i = 1, . . . , `.
Observación 13. Al comparar las condiciones de Optimalidad de KKT con la condición
(C) del caso con restricciones de igualdad podemos notar una pequeña “inconsistencia” en el
signo asociado al multiplicador λi . Naturalmente, esto no tiene influencia en los resultados
aquı́ expuestos pues se trata simplemente de una convención.
Veamos como se usan las condiciones de primer orden (KKT) mediante un ejemplo.
Ejemplo 6. Considere el problema
min − 3x + y − z 2
s.a.
− x − 2y + z 2 = 0
x + y + z ≤ 0.
Escribir las ecuaciones de KKT para el problema y encontrar el o los candidatos a soluciones
óptimas del problema.
Solución: Identifiquemos primero los elementos para aplicar el Teorema 7. Se tiene que
m = 1, ` = 1, f (x, y, z) = −3x + y − z 2 , g(x, y, z) = −x − 2y + z 2 , h(x, y, z) = x + y + z.
Además,
∇f (x, y, z) = (−3, 1, −2z),
∇g(x, y, z) = (−1, −2, 2z)
∇h(x, y, z) = (1, 1, 1), .
Luego, las condiciones de KKT en este caso corresponden a encontrar un vector (x, y, z, λ, µ)
tal que
 
   
0
1
−1
   


 
 1  + λ −2 + µ 1 = 0 ,
   

 

2z
1
0
−2z

−3

µ ≥ 0.
Es decir,



−3 − λ + µ






1 − 2λ + µ



−2z + 2λz + µ





µ(x + y + z)





µ
=0
=0
=0
=0
≥ 0.
14
De las dos primeras ecuaciones se deduce el valor de los multiplicadores µ = 7 > 0, λ = 4.
Conocidos los multiplicadores y usando la tercera ecuación, se tiene que z = − 67 . Usando
la holgura complementaria, se obtiene que x + y − 7/6 = 0. Por último, para encontrar los
valores de x e y, es necesario resolver el sistema de ecuaciones:
2
7
−x − 2y +
=0
6
7
x + y − = 0.
6
Luego x =
35
36
ey=
7
36 .
Es decir, el punto candidato a óptimo (local a priori) es (x0 , y0 , z0 ) =
7
7
( 35
36 , 36 , − 6 ). Queda como ejercicio comprobar que la condición de calificación de restricciones
se cumple en (x0 , y0 , z0 )
Una observación interesante es la siguiente. El conjunto factible en este caso es no acotado, luego se necesita un criterio de segundo orden para saber si se trata efectivamente de un
mı́nimo. Sin embargo, como sabemos que el multiplicador µ es estrictamente positivo, podemos convertir este problema particular en uno de dos variables: minimizar 3x + y − (x + y)2
sujeto a la restricción −x − 2y + (x + y)2 = 0. Convénzase gráficamente que el punto encontrado es un mı́nimo.
Ejemplo 7. Analizar, utilizando las condiciones de KKT, el problema
max
x − e−y
sin(x) + y ≤ 0
0≤x≤π
Solución: El problema a resolver es equivalente al siguiente:
−min e−y − x
sin(x) + y ≤ 0
x−π ≤0
−x ≤ 0
Si f (x, y) = e−y − x, h1 (x, y) = sin(x) + y, h2 (x, y) = x − π, h3 (x, y) = −x, entonces los
gradientes respectivamente son:
∇f (x, y) = (−1, −e−y ),
∇h1 (x, y) = (cos(x), 1),
∇h2 (x, y) = (1, 0),
∇h3 (x, y) = (−1, 0).
15
Las condiciones de KKT son entonces h1 (x, y) ≤ 0, h2 (x, y) ≤ 0, h3 (x, y) ≤ 0 y
−1 + µ1 cos(x) + µ2 − µ3 = 0
−e−y + µ1 = 0
µ1 (sin(x) + y) = 0
µ2 (x − π) = 0
−µ3 x = 0
µ1 ≥ 0
µ2 ≥ 0
µ3 ≥ 0.
Como µ1 = e−y , entonces µ1 > 0 y, por holgura complentaria, y = −sen(x). De la primera
ecuación se obtiene que µ2 = 1 − esen(x) cos(x) + µ3 .
• Si x = π, entonces µ3 = 0 y µ2 = 1 − esen(π) cos(π) = 2 > 0. Luego el punto (π, 0, 1, 2, 0)
es solución del sistema y (π, 0) es candidato a óptimo.
• Si µ3 > 0 entonces x = 0, y = 0 y µ2 = µ3 > 0. Por holgura complementaria x = π, una
contradicción.
• Si µ3 = 0 con x 6= π entonces µ2 = 1 − esen(x) cos(x) = 0. Esta ecuación tiene dos
soluciones tales que 0 ≤ x ≤ π: x = 0 y x = x∗ con 0 < x∗ < π (¿Por qué?). Luego, hay
dos puntos crı́ticos más: (0, 0, 1, 0, 0) y (x∗ , −sen(x∗ ), esen(x∗ ) , 0, 0), implicando que (0, 0) y
(x∗ , −sen(x∗ )) también son candidatos.
Como la región factible es no acotada, necesitamos a priori un criterio de segundo orden.
Sin embargo, es fácil darse cuenta que, como se tiene siempre que y = −sen(x), la función
φ(x) = x − esen(x) es decreciente en el intervalo [0, x∗ ] y luego creciente en el intervalo [x∗ , π]
con φ(0) = −1 y φ(π) = π. Esto nos permite concluir que el punto (π, 0) es, de hecho, un
máximo global.
Ejemplo 8. Considere el problema
min
(x − 3)2 + (y − 2)2
x2 + y 2 ≤ 5
2x + y ≤ 6
x + 2y ≤ 4
x≥0
y≥0
16
Usar un método gráfico para encontrar el óptimo global del problema y verificar las condiciones de KKT en ese punto.
Solución: Para aplicar el teorema, ponemos el problema en la forma:
min
(x − 3)2 + (y − 2)2
x2 + y 2 − 5 ≤ 0
2x + y − 6 ≤ 0
x + 2y − 4 ≤ 0
−x ≤ 0
−y ≤ 0
Notemos que el óptimo para el problema irrestricto es (3, 2), sin embargo, éste no es un
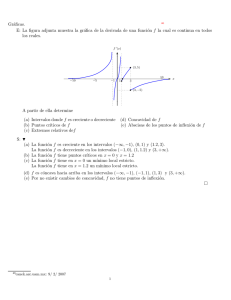
punto factible. Ahora, usando el método gráfico, tenemos que según la Figura 2, el óptimo se
alcanza en (x, y) = (2, 1), es decir, la circunferencia de menor radio que interceca el conjunto
de factibilidad es aquella que pasa por este punto. Notemos además que en este punto las
restricciones 1 y 3 son activas.
Ahora verifiquemos que este punto satisface las condiciones de KKT.
Las condiciones de KKT son entonces
2(x − 3) + 2µ1 x + 2µ2 + µ3 − µ4 = 0
2(y − 2) + 2µ1 y + µ2 + 2µ3 − µ5 = 0
µ1 (x2 + y 2 − 5) = 0
µ2 (2x + y − 6) = 0
µ3 (x + 2y − 4) = 0
µ4 (−x) = 0
µ5 (−y) = 0
µi ≥ 0
i = 1, 2, 3, 4, 5.
Verifiquemos que los multiplicadores de KKT satisfacen las condiciones de no-negatividad en
el punto (2, 1). Holgura complementaria implica que
µ2 = µ4 = µ5 = 0 ,
17
Figura 2. Método gráfico.
lo que conduce al siguiente sistema,
2(x − 3) + 2µ1 x + µ3 = 0
2(y − 2) + 2µ1 y + 2µ3 = 0
x2 + y 2 = 5
x + 2y = 4
µ1 , µ3 ≥ 0
Reemplazando (x, y) = (2, 1), tenemos que µ1 = 1/3 ≥ 0 y µ3 = 2/3 ≥ 0.