Módulo. Calculo Diferencial
Unidad 3
Programa educativo:
Semestre:
Desarrollo de Software
Primero
Módulo:
Bloque:
Cálculo Diferencial
2
Ciclo escolar:
Nombre del docente:
2021-1
Carlos Javier Arteaga Vega
UNIDAD 3 DERIVACIÓN
Competencia general de la unidad:
Utilizar el concepto de derivada de una función como un
límite en particular, posteriormente, emplear las
propiedades de la derivada y sus interpretaciones gráficas
de dichas propiedades.
Competencia específica de la unidad:
Aplica el concepto de la derivada para analizar el
comportamiento de las funciones y sus aplicaciones,
utilizando las propiedades de las derivadas.
Pág. 2
Módulo. Calculo Diferencial
Unidad 3
Calendario de Actividades
Unidad 3
Nombre de la actividad
Fecha de entrega
Actividad 1 Cambio de variación
Actividad 2 Derivación de funciones trascendentes
Actividad 3 Derivación de orden implícita
Evidencia de Aprendizaje Aplicación de la derivada
9 al 12 de mayo del 2021
13 al 16 de mayo del 2021
17 al 20 de mayo del 2021
21 al 26 de mayo del 2021
Aprendizaje(s)/Logros:
Identificar el concepto de derivada de una función y su relación con el límite.
Estudiar la derivada como un límite actuando sobre funciones.
Aplicar las propiedades de límites al cálculo de derivadas de funciones.
Actividad:
Actividad 1. Cambio de variación
Tema(s):
3.1.1 Concepto de la derivada
3.1.2 Propiedades de la derivada
Escala a considerar y fechas de entrega
0-100%
9 al 26 de mayo del 2021
0-80%
27 de mayo al 2 de junio del 2021
0- 70%
3 al 16 de junio a las 23:55 hrs.
(tiempo de la ciudad de México)
Estrategia de enseñanza-aprendizaje:
Enseñanza
Monitorea la participación de cada uno de los estudiantes en el foro.
Retroalimenta a cada estudiante, identificando fortalezas y áreas de oportunidad en
la identificación de la aplicación de los cambios de variación en distintas situaciones
cotidianas.
Pág. 3
Módulo. Calculo Diferencial
Unidad 3
Aprendizaje
El estudiante reflexiona y retroalimenta a través del intercambio de conceptos del
tema en debate.
El estudiante reflexiona sobre su trabajo y llega a unas conclusiones significativas y
relevantes.
Logros:
Identificar la derivada de una función como el proceso al límite de dicha función dentro
de un contexto cotidiano.
Criterios de evaluación:
Formato del documento (5%)
El documento en Word incluye portada, índice, introducción, el desarrollo,
conclusiones y referencia de la bibliografía y del software utilizado en formato
APA.
Desarrollo / contenido (80%)
Los ejercicios son resueltos de acuerdo con las instrucciones
Conclusión (5%)
Incluye una conclusión de la actividad
Retroalimentación a uno de sus compañeros (10%)
Realiza la retroalimentación de un compañero de acuerdo con las instrucciones
Objetivo o Propósito de la actividad de aprendizaje:
Tener un primer acercamiento a la definición de derivada, en específico, a la variación de una
función real representada en diferentes contextos de la vida cotidiana.
Indicaciones de la actividad:
1. Revisa los problemas y/o ejercicios que se proponen para el desarrollo de la actividad.
2. Apóyate en los recursos del contenido de la unidad, en los recursos que se te
recomendarán en la sección fuentes de consulta y en tu propia investigación en fuentes
confiables.
3. Elabora un documento en Word con la solución de cada uno de los problemas y/o
ejercicios, anexa procedimiento completo y la conclusión solicitada. Si la actividad no
se integra en formato Word se evaluará con 1 (uno) y se perderá un intento.
4. Utiliza un editor de ecuaciones y un programa para graficar en el planteamiento de
solución para los problemas solicitados.
5. Incluye las referencias de tus fuentes de información y software utilizado en formato APA.
6. Guarda tu archivo con la nomenclatura CDI_U3_A1_XXYZ. Sustituye las XX por las
Pág. 4
Módulo. Calculo Diferencial
Unidad 3
iniciales de tu primer nombre, la Y por la inicial de tu apellido paterno y la Z por la inicial
de tu segundo apellido.
7. Consulta los criterios de evaluación y verifica que tu actividad cumple con cada uno de
ellos.
8. Ingresa al foro Actividad 1. Cambio de variación y en una primera aportación adjunta tu
archivo Word donde has respondido a cada uno de los planteamientos.
9. Entrega tu trabajo en la herramienta correspondiente dentro del aula virtual, de acuerdo
al calendario establecido en esta planeación.
10. Realiza una segunda aportación, revisando la aportación de alguno de tus compañeros,
aceptando o rechazando su respuesta, argumentando el por qué, y tomando como base
alguna bibliografía de fuentes fidedignas o fuentes especializadas.
Ejercicios por resolver:
1. Investiga mínimo de tres diferentes fuentes confiables; lee la información y posteriormente
realiza una infografía donde expliques el concepto de la derivada.
2. Menciona 3 maneras para interpretar la derivada de la función 𝑓′(𝑥) en la siguiente tabla:
1.
2.
3.
3. Investiga uno o dos ejemplos colocando imágenes y una breve explicación, mostrando
así donde se aplica la derivada en la vida cotidiana y/o en el campo laboral.
4. Descifre el siguiente texto en base al código y escriba en lo sombreado la letra que
corresponda a cada símbolo.
Pág. 5
Módulo. Calculo Diferencial
Unidad 3
♣
Símbolo
╓
♥
♫
→
▲
☼
☺
꞊
ﭞ
Letra
P
L
D
A
S
U
Q
F
E
Símbolo
◄
∞
▓
♀
█
╬
ᴥ
Ѻ
¶
─
Ξ
Letra
R
G
V
N
H
M
Y
T
C
B
O
I
L
A
D
E
R
I
V
A
D
A
♥
→
♫
ﭞ
◄
♣
▓
→
♫
→
E
S
U
N
A
ﭞ
▲
☼
♀
→
H
E
R
R
A
M
I
E
N
T
A
█
ﭞ
◄
◄
→
╬
♣
ﭞ
♀
Ѻ
→
Q
U
E
A
Y
U
D
A
A
☺
☼
ﭞ
→
ᴥ
☼
♫
→
→
R
E
S
O
L
V
E
R
◄
ﭞ
▲
Ξ
♥
▓
ﭞ
◄
P
R
O
B
L
E
M
A
S
╓
◄
Ξ
─
♥
ﭞ
╬
→
▲
Pág. 6
Módulo. Calculo Diferencial
Unidad 3
D
I
V
E
R
S
O
S
E
N
♫
♣
▓
ﭞ
◄
▲
Ξ
▲
ﭞ
♀
L
O
S
Q
U
E
S
E
♥
Ξ
▲
☺
☼
ﭞ
▲
ﭞ
I
N
V
O
L
U
C
R
A
N
♣
♀
▓
Ξ
♥
☼
¶
◄
→
♀
C
A
M
B
I
O
S
D
E
¶
→
╬
─
♣
Ξ
▲
♫
ﭞ
V
A
R
I
A
C
I
O
N
▓
→
◄
♣
→
¶
♣
Ξ
♀
Producto por entregar:
Documento en formato WORD que subirás como tarea a la plataforma bajo la siguiente
estructura:
I.
Portada con datos de la asignatura y estudiante
II.
Ejercicios resueltos con el desarrollo incluido
III.
Conclusión
IV.
Fuentes de consulta en formato APA
Instrumento de evaluación
Escala de evaluación para la Actividad 1
Pág. 7
Módulo. Calculo Diferencial
Carrera:
Asignatura:
Semestre:
Unidad:
Actividad:
Unidad 3
Desarrollo de software
Cálculo Diferencial
1
Unidad 3. Derivación
Actividad 1. Cambio de variación
Instrucciones: Anote en cada casilla los puntos obtenidos por el (la) estudiante en cada criterio
por evaluar.
Criterios de evaluación
Puntaje
por criterio
Puntaje
obtenido
Formato del documento
1. El documento en Word incluye portada, índice,
introducción, el desarrollo, conclusiones y referencia de la
bibliografía y del software utilizado en formato APA.
5
Desarrollo / contenido
1. El ejercicio 1 es resuelto de acuerdo con las instrucciones
20
2. El ejercicio 2 es resuelto de acuerdo con las instrucciones
20
3. El ejercicio 3 es resuelto de acuerdo con las instrucciones
20
4. El ejercicio 4 es resuelto de acuerdo con las instrucciones
20
Conclusión
5. Incluye una conclusión de la actividad
Retroalimentación
6. Realiza la retroalimentación de un compañero de acuerdo
con las instrucciones
Puntaje total
5
10
100
Fuentes de Consulta:
Galván Sánchez, D. A., Cienfuegos Zurita, D. E., Romero Álvarez, J. d., & Fabela
Rodríguez, M. d. (s.f.). Calculo Diferencial. Un enfoque constructivista para el desarrollo
de las competencias mediante la reflexión y la interacción (segunda ed.). México.
P., (2007). Calculo. Pearson Educación.
Pág. 8
Módulo. Calculo Diferencial
Unidad 3
Calendario de Actividades
Unidad 3
Nombre de la actividad
Fecha de entrega
Actividad 1 Cambio de variación
Actividad 2 Derivación de funciones trascendentes
Actividad 3 Derivación de orden implícita
Evidencia de Aprendizaje Aplicación de la derivada
9 al 12 de mayo del 2021
13 al 16 de mayo del 2021
17 al 20 de mayo del 2021
21 al 26 de mayo del 2021
Actividad:
Actividad 2. Derivada de Funciones Trascendentes
Tema(s):
3.2. Funciones Trascendentes
3.2.1. Funciones exponenciales
logaritmos
3.2.2. Funciones trigonométricas
3.2.3. Funciones hiperbólicas
Escala a considerar y fechas de entrega
y
0-100%
9 al 26 de mayo.
0-80%
27 de mayo al 2 de junio.
0- 70%
3 al 16 de junio a las 23:55 hrs.
(tiempo de la ciudad de México)
Estrategia de enseñanza-aprendizaje:
El docente
Retroalimenta a cada estudiante identificando sus fortalezas y áreas de oportunidad
para realizar diferentes ejercicios y problemas donde se apliquen derivadas de
funciones trascendentes, incluyendo su gráfica.
Motiva al estudiante a utilizar los recursos sobre los temas a trabajar contenidos en
el Aula virtual.
Promueve en los estudiantes el autoaprendizaje, invitándolos a buscar información y
recursos que complementen los contenidos del Aula virtual.
El estudiante
Resuelve ejercicios y problemas donde tiene que encontrar la derivada de una función
transcendente usando su definición, propiedades y aplicando fórmulas para
calcularla, recordando los conocimientos y habilidades adquiridas en las Unidades 1
y 2, así como realizando, si es necesario, la gráfica de la misma.
Hace uso de software matemático para reforzar la comprensión de los temas.
Logros:
Pág. 9
Módulo. Calculo Diferencial
Unidad 3
Identificar que el límite es único.
Relacionar la derivada con el estudio de la velocidad instantánea o también al
encontrar la recta tangente a una curva cualquiera.
Desarrollar la capacidad de resolución de ejercicios de derivadas de funciones.
Identificar el tipo de función trascendente a la que corresponde y aplicar la fórmula
más adecuada para poder derivarla.
Criterios de evaluación:
Formato del documento (15%)
Portada, Índice, referencia de la bibliografía y del software utilizado en formato
APA. La portada incluye varios datos personales y de la asignatura.
El documento tiene alineación justificada, números de página y no presenta
faltas de ortografía.
Hace uso de herramientas de software para presentar su actividad: procesador
de texto, editor de ecuaciones, software para graficar. También cita el software
que utilizó
Desarrollo / contenido (80%)
Identifica e interpreta con claridad los datos planteados en los ejercicios y tiene
certeza de lo que se debe resolver. Demuestra total comprensión del tema.
Cada ejercicio contiene procedimientos, no tiene espacios vacíos, es claro (se
facilita seguir el razonamiento empleado para resolver el problema), coherente
y es resuelto de acuerdo con las instrucciones.
Conclusión (5%)
Incluye una Conclusión de la actividad.
Objetivo o Propósito de la actividad de aprendizaje:
Mediante esta actividad lograrás contestar algunas preguntas y resolver problemas con funciones
transcendentes, calculando su derivada, utilizando un formulario y haciendo la gráfica
correspondiente.
Indicaciones de la actividad:
1. Revisa las preguntas y los problemas que se proponen para el desarrollo de la actividad.
2. Apóyate en los recursos del contenido de la Unidad, en los recursos que se te recomendarán
en la sección fuentes de consulta y en tu propia investigación en fuentes confiables.
3. Elabora un documento en Word con la respuesta de las preguntas y la solución de cada uno
de los problemas, anexa el procedimiento completo y la conclusión solicitada. Si la actividad
no se integra en formato Word se evaluará con 1 (uno) y se perderá un intento.
4. Utiliza un editor de ecuaciones y un programa para graficar en el planteamiento de
Pág. 10
Módulo. Calculo Diferencial
Unidad 3
solución, para los problemas solicitados
5. Incluye las referencias de tus fuentes de información y software utilizado en Formato APA.
6. Guarda tu archivo con la nomenclatura CDI_U2_A2_XXYZ. Sustituye las XX por las iniciales
de tu primer nombre, la Y por la inicial de tu apellido paterno y la Z por la inicial de tu segundo
apellido.
7. Consulta los criterios de evaluación y verifica que tu actividad cumple con cada uno de ellos.
8. Entrega tu trabajo en la herramienta correspondiente dentro del Aula virtual, de acuerdo al
calendario establecido en esta Planeación.
Ejercicios por resolver:
EJERCICIO 1.
CONTESTA LAS SIGUIENTES PREGUNTAS:
1.- ¿Qué significa: Funciones trascendentes en Matemáticas?
2.- ¿Por qué consideras que son importantes las Funciones trascendentes?
EJERCICIO 2.
En una empresa automotriz, la velocidad con la que se ejecuta un programa del Departamento
de Almacén, está dada por la función:
𝒈(𝒙) = −𝟓 𝒔𝒆𝒏 (−𝟐𝒙)
donde se especifica que “g” corresponde a los datos informáticos y “x” es el tiempo en
segundos.
Se pide encontrar cuál es la derivada.
EJERCICIO 3.
Una población de insectos crece conforme a la función:
Pág. 11
Módulo. Calculo Diferencial
𝑓(𝑥) = 𝑒 4𝑥
Unidad 3
3
donde x representa el tiempo que transcurre, en meses.
Se quiere saber:
a) ¿Cuál es la derivada?
b) ¿Cuál sería la función a utilizar, para encontrar el segundo mes?
EJERCICIO 4.
¿Cuál será la velocidad a la que corre un programa, que está definido por la función:
𝑔(𝑥) = ln(2𝑥 3 + 1) ?
EJERCICIO 5.
Analiza la siguiente función:
3
𝑎𝑟𝑐𝑠𝑒𝑛(5𝑥 3 ) − 5
5
Después se pide realizar lo siguiente:
a) Describe el procedimiento utilizado para encontrar 𝑓´(𝑥).
b) Dibuja las gráficas de 𝑓(𝑥) 𝑦 𝑓´(𝑥).
EJERCICIO 6.
Se pide lo siguiente:
a) Encontrar la ecuación de la recta que es tangente en el punto indicado, con la siguiente
función:
𝑓(𝜃) = 4 𝑠𝑒𝑛 (𝜃) − 𝜃
𝑃𝑢𝑛𝑡𝑜 ( 0 , 0 )
b) Muestra la gráfica de la función y la recta tangente en el punto dado, que obtuviste.
NOTA: Se puede obtener la recta tangente si se conoce un punto que pertenece a la recta, junto
con su pendiente. Al derivar una función se puede obtener su pendiente.
Pág. 12
Módulo. Calculo Diferencial
Unidad 3
La ecuación de una recta que pasa por el punto (𝑥1 , 𝑦1 ) está dada por:
𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1 )
Producto por entregar:
Documento en formato WORD que subirás como de tarea a la plataforma bajo la siguiente
estructura:
I.
Portada con los datos del alumno y la asignatura.
II.
Índice
III.
Introducción
IV.
Ejercicios resueltos con todo el desarrollo incluido
V.
Conclusión
VI.
Fuentes de consulta en Formato APA.
Instrumento de evaluación
Escala de evaluación para la Actividad 2
Carrera:
Asignatura:
Semestre:
Unidad:
Actividad:
Desarrollo de software
Cálculo Diferencial
1
Unidad 3. Derivación
Actividad 2. Derivada de Funciones Trascendentes
Instrucciones: Anote en cada casilla los puntos obtenidos por el (la) estudiante en cada criterio
por evaluar.
Pág. 13
Módulo. Calculo Diferencial
Unidad 3
Criterios de evaluación
Puntaje
por criterio
Puntaje
obtenido
Formato del documento
1. Portada completa, Índice, Introducción, Referencias de la
bibliografía y del software utilizado, aplicando el Formato APA.
5
2. El documento tiene alineación justificada, números de página y
no presenta faltas de ortografía.
5
3. Hace uso de herramientas de software para presentar su
actividad: procesador de texto, editor de ecuaciones, software
para graficar. También cita el software que utilizó.
Desarrollo / contenido
5
4. Identifica el tipo de función y la regla de derivación que debe
utilizarse para calcular la derivada.
5
5. Aplica correctamente la o las reglas de derivación para hallar las
derivadas presentadas.
5
6. El Ejercicio 1, contiene las respuestas adecuadas y son
coherentes a las preguntas planteadas.
10
7. El Ejercicio 2, contiene todo el procedimiento, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado para
resolver el problema), coherente y es resuelto de acuerdo con
las instrucciones.
8. El Ejercicio 3, contiene procedimientos, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado para
resolver el problema), coherente y es resuelto de acuerdo con
las instrucciones.
9. El Ejercicio 4, contiene procedimientos, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado para
resolver el problema), coherente y es resuelto de acuerdo con
las instrucciones.
10. El Ejercicio 5, contiene procedimientos, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado para
resolver el problema), coherente y es resuelto de acuerdo con
las instrucciones.
11. El Ejercicio 6, contiene procedimientos, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado para
resolver el problema), coherente y es resuelto de acuerdo con
las instrucciones.
Conclusión
12. Incluye una Conclusión de lo que se aprendió al realizar la
actividad.
Puntaje total
10
10
10
15
15
5
100
Pág. 14
Módulo. Calculo Diferencial
Unidad 3
Fuentes de consulta:
Básica:
Apóstol, T. M. (2008). Calculus. España: Reverté.
Geogebra. (s / f) https://www.geogebra.org/
Larson, R. E. (2010). Cálculo de una variable. México: Mc Graw Hill.
Leithold, L. (2009). El Cálculo. México: Oxford University Press.
Stewart, James. (2008). Cálculo. Trascendentes tempranas. México: Cengage Learning.
Complementaria:
-
Zill, D. (2011). Cálculo; Trascendentes tempranas, 4a edición. México. Mc Graw Hill.
Pág. 15
Módulo. Calculo Diferencial
Unidad 3
Calendario de Actividades
Unidad 3
Nombre de la actividad
Fecha de entrega
Actividad 1 Cambio de variación
Actividad 2 Derivación de funciones trascendentes
Actividad 3 Derivación de orden implícita
Evidencia de Aprendizaje Aplicación de la derivada
9 al 12 de mayo del 2021
13 al 16 de mayo del 2021
17 al 20 de mayo del 2021
21 al 26 de mayo del 2021
Actividad:
Actividad 3. Derivación de orden superior e implícita
Tema(s):
Escala a considerar y fechas de entrega
3.3 Derivación de orden superior
3.4 Derivación Implícita
0-100%
9 al 26 mayo de 2021
0-80%
27 de mayo al 2 de junio de 2021
0- 70%
3 al 16 de junio a las 23:55 hrs.
(tiempo de la ciudad de México)
Estrategia de enseñanza-aprendizaje:
El docente
Retroalimenta a cada estudiante identificando sus fortalezas y áreas de oportunidad
para derivar de una función de orden superior o implícita.
Motiva al estudiante a utilizar los recursos sobre los temas a trabajar contenidos en
el aula virtual.
Promueve en los estudiantes el autoaprendizaje, invitándolos a buscar información y
recursos que complementen los contenidos del aula virtual.
El alumno
Resuelve ejercicios y problemas donde tiene que encontrar la derivada de orden
superior o implícita de una función.
Hace uso de software matemático para reforzar la comprensión de los temas.
Logros:
Identifica y resuelve derivadas de orden superior
Pág. 16
Módulo. Calculo Diferencial
Unidad 3
Identifica y resuelve derivadas implícitas
Criterios de evaluación:
Formato del documento (15%)
Portada, índice, referencia de la bibliografía y del software utilizado en formato
APA. La portada incluye los datos personales y de la asignatura.
El documento tiene alineación justificada, números de página y no presenta faltas
de ortografía
Hace uso de herramientas de software para presentar su actividad: procesador de
texto, editor de ecuaciones.
Desarrollo / contenido (80%)
Identifica e interpreta con claridad los datos planteados en los ejercicios y tiene
certeza de lo que se debe resolver. Demuestra total comprensión del tema.
Los ejercicios contienen procedimientos, no tiene espacios vacíos, es claro (se
facilita seguir el razonamiento empleado para resolver el problema), coherente y
es resuelto de acuerdo con las instrucciones.
Conclusión (5%)
Incluye una conclusión de la actividad.
Indicaciones de la actividad:
1. Revisa los problemas y/o ejercicios que se proponen para el desarrollo de la actividad.
2. Apóyate en los recursos del contenido de la unidad, en los recursos que se te recomendarán
en la sección fuentes de consulta y en tu propia investigación en fuentes confiables.
3. Elabora un documento en Word con la solución de cada uno de los problemas y/o ejercicios,
anexa procedimiento completo y la conclusión solicitada. Si la actividad no se integra en
formato Word se evaluará con 1 (uno) y se perderá un intento.
4. Utiliza un editor de ecuaciones
5. Incluye las referencias de tus fuentes de información y software utilizado en formato APA.
6. Guarda tu archivo con la nomenclatura CDI_U3_A3_XXYZ. Sustituye las XX por las iniciales
de tu primer nombre, la Y por la inicial de tu apellido paterno y la Z por la inicial de tu segundo
apellido.
7. Consulta los criterios de evaluación y verifica que tu actividad cumple con cada uno de ellos.
8. Entrega tu trabajo en la herramienta correspondiente dentro del aula virtual, de acuerdo al
calendario establecido en esta planeación.
Ejercicios por resolver:
Pág. 17
Módulo. Calculo Diferencial
Unidad 3
Sección 1: Derivación de Orden Superior
Encontrar
𝑑3𝑦
𝑑𝑥 3
de las siguientes funciones:
a) 𝑦 = 𝑠𝑒𝑛(𝑥 3 )
b) 𝑦 = (3 − 5𝑥)5
Sección 2. Aplicación Derivación de Orden Superior (Movimiento Rectilíneo)
a) El movimiento de una partícula está definido por 𝑥 = 2𝑡 3 − 10𝑡 2 + 15𝑡 + 5 donde “x” y “t”
se expresan en metros y segundos respectivamente. Determine a) Cuándo la velocidad
es cero, b) cuándo la aceleración es cero.
b) Dos partículas se mueven a lo largo de un eje coordenado, sus distancias en pies están
dadas por 𝑆1 = 𝑡 3 − 6𝑡 2 − 36𝑡 − 40 y 𝑆2 = 𝑡 3 − 9𝑡 2 + 24𝑡 − 8. Determine: a) cuándo serán
sus velocidades iguales. b) la aceleración de cada partícula, cuándo las velocidades son
iguales.
Sección 3. Derivación Implícita
Encuentre 𝑑𝑦/𝑑𝑥 de las siguientes funciones:
a) 4𝑥 3 + 7𝑥𝑦 2 = 2𝑦 3
b) 𝑥𝑦 + 𝑠𝑒𝑛(𝑥𝑦) = 1
Sección 4. Aplicación Derivación Implícita (Ecuación de la recta)
a) Encuentre la ecuación de la recta tangente de la curva: 𝑥 3 𝑦 + 𝑦 3 𝑥 = 30 en el punto (1,3)
b) Encuentre la ecuación de la recta tangente de la curva: 𝑠𝑒𝑛(𝑥𝑦) = 𝑦 en el punto (/2, 1)
Producto por entregar:
Documento en formato WORD que subirás como de tarea a la plataforma bajo la siguiente
estructura:
I.
II.
III.
IV.
Portada con datos de la asignatura y estudiante
Ejercicios resueltos con el desarrollo incluido
Conclusión
Fuentes de consulta en formato APA
Pág. 18
Módulo. Calculo Diferencial
Unidad 3
Instrumento de evaluación
Escala de evaluación para la Actividad 3
Carrera:
Asignatura:
Semestre:
Unidad:
Actividad:
Desarrollo de software
Cálculo Diferencial
1
Unidad 3. Derivación
Actividad 3. Derivadas de orden superior e Implícitas
Instrucciones: Anote en cada casilla los puntos obtenidos por el (la) estudiante en cada criterio
por evaluar.
Criterios de evaluación
Formato del documento
1. Portada, índice, referencia de la bibliografía y del software
utilizado en formato APA. La portada incluye los datos
personales y de la asignatura.
2. El documento tiene alineación justificada, números de
página y no presenta faltas de ortografía
3. Hace uso de herramientas de software para presentar su
actividad: procesador de texto, editor de ecuaciones,
software para graficar. Y cita el software que utilizó
Desarrollo / contenido
4. La sección 1, contiene procedimientos, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado
para resolver el problema), coherente y es resuelto de
acuerdo con las instrucciones.
5. La sección 2, contiene procedimientos, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado
para resolver el problema), coherente y es resuelto de
acuerdo con las instrucciones.
6. La sección 3, contiene procedimientos, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado
para resolver el problema), coherente y es resuelto de
acuerdo con las instrucciones.
7. La sección 4, contiene procedimientos, no tiene espacios
vacíos, es claro (se facilita seguir el razonamiento empleado
para resolver el problema), coherente y es resuelto de
acuerdo con las instrucciones.
Conclusión
8. Incluye una conclusión de la actividad.
Puntaje total
Puntaje
por criterio
Puntaje
obtenido
5
5
5
20
20
20
20
5
100
Fuentes de consulta:
Pág. 19
Módulo. Calculo Diferencial
Unidad 3
Beer, Johnstone, Conrwell, (2010). Mecánica Vectorial para Ingenieros Dinamcia, Mc
Graw Hill
Pircell, Varberg Rigdon. (2007). Cálculo diferencial e integral. Pearson Educación.
Leithold, L. (2009). El Cálculo. México: Oxford University Press.
Matemacias profe Alex, 2020 Derivadas de orden superior Introduccion. [video]. Youtube.
https://www.youtube.com/watch?v=sMct2JvYDlE
Matemacias profe Alex, 2020 Derivadas de orden superior, ejemplo 2 trigonométricas sen
y cos. [video]. Youtube. https://www.youtube.com/watch?v=kQYEaU99I44
Matemacias profe Alex, 2018 Derivada implícita Introducción. [video]. YouTube.
https://www.youtube.com/watch?v=u0BP7ZMRsms
Matemacias profe Alex, 2018 Derivada implícita Ejemplo 1. [video]. YouTube.
https://www.youtube.com/watch?v=RAzsJFsIzzQ
Pág. 20
Módulo. Calculo Diferencial
Unidad 3
Calendario de Actividades
Unidad 3
Nombre de la actividad
Fecha de entrega
Actividad 1 Cambio de variación
Actividad 2 Derivación de funciones trascendentes
Actividad 3 Derivación de orden implícita
Evidencia de Aprendizaje Aplicación de la derivada
9 al 12 de mayo del 2021
13 al 16 de mayo del 2021
17 al 20 de mayo del 2021
21 al 26 de mayo del 2021
Actividad:
Evidencia de aprendizaje. Aplicación de la derivada
Tema(s):
3.1.1 Concepto de la derivada
3.1.2 Propiedades de la derivada
3.2.1. Funciones exponenciales
logaritmos
3.2.2. Funciones trigonométricas
3.2.3. Funciones hiperbólicas
3.3. Derivadas de Orden superior
3.4 derivación implícita
Escala a considerar y fechas de entrega
y
0-100%
9 al 26 de mayo del 2021
0-80%
27 de mayo al 2 de junio del 2021
0- 70%
3 al 16 de junio a las 23:55 hrs.
(tiempo de la ciudad de México)
Estrategia de enseñanza-aprendizaje:
Enseñanza:
Ejemplificar la existencia de funciones no diferenciables, de lo cual se concluye que
la continuidad no es una condición suficiente para ser derivable.
Mencionar los tipos de máximos y mínimos que una función puede tener, así como
también modelar un problema que demande la optimización de una función.
Proponer problemas básicos dentro del cálculo diferencial, como son las reglas de
diferenciación (teoremas).
Aprendizaje:
Repasar los conceptos aprendidos en la unidad sobre la derivada de una función.
Aplicar sus conocimientos a la solución de problemas cortos seleccionando de
respuestas múltiples o relacionando respuestas.
Dar respuesta a ejercicios a partir de visualizar las gráficas de funciones bajo
inspección.
Afrontar problemas de la materia que demandan modelar y optimizar funciones.
Pág. 21
Módulo. Calculo Diferencial
Unidad 3
Afrontar problemas de cálculo diferencial que demandan modelar situaciones bajo
hipótesis dadas, optimizar funciones y determinar la naturaleza de los puntos óptimos
mediante criterios del cálculo diferencial
Logros:
El estudiante reafirmará los conocimientos fundamentales sobre la derivada de una
función. Reconocerá que existen funciones que no son diferenciable en algún punto.
El estudiante modelará un problema básico y optimizará la función objetivo del
problema.
El estudiante identificará la derivada como una herramienta útil para optimizar
funciones. Reconocerá los tipos de puntos críticos de una función, máximos y
mínimos y puntos de inflexión.
Aplicará conceptos como básicos como regla de la cadena, composición de
funciones, funciones inversas, derivadas de funciones transcendentales, derivadas
de funciones potencia que son reglas fundamentales para derivar una función.
Criterios de evaluación:
Formato y estructura del documento (5%): El documento en Word incluye portada,
índice, introducción, el desarrollo, conclusiones y referencia de la bibliografía y del
software utilizado en formato APA.
Respuestas y desarrollo de actividades (90%): Los ejercicios 1,2, 3 y 4 son
resueltos de acuerdo con las instrucciones.
Conclusión (5%): Incluye una conclusión propia de la actividad.
Objetivo o Propósito de la actividad de aprendizaje:
Mediante esta actividad identificarás a la derivada como una operación importante sobre
funciones que tiene una interpretación distinguida en diversos ámbitos. Reconocerás que existen
funciones continuas, pero no diferenciables en todo punto. Repasarás las reglas básicas para
obtener la función derivada y los teoremas fundamentales para el cálculo de la derivada. Podrás
aplicar las reglas de cálculo y determinación de la derivada para optimizar funciones que tienen
una interpretación particular en un determinado contexto.
Descripción de la actividad/ indicaciones de la actividad:
1. Revisa los problemas y/o ejercicios que se proponen para el desarrollo de la actividad.
2. Apóyate en los recursos del contenido de la unidad, en los recursos que se te recomendarán
en la sección fuentes de consulta y en tu propia investigación en fuentes confiables.
3. Elabora un documento en Word con la solución de cada uno de los problemas y/o ejercicios,
anexa procedimiento completo y la conclusión solicitada. Si la actividad no se integra en formato
Word se evaluará con 1 (uno) y se perderá un intento.
Pág. 22
Módulo. Calculo Diferencial
Unidad 3
4. Utiliza el editor de ecuaciones y un programa para graficar en el planteamiento de solución
para los problemas solicitados
5. Incluye las referencias de tus fuentes de información y software utilizado en formato APA.
6. Guarda tu archivo con la nomenclatura CDI_U3_EA_XXYZ. Sustituye las XX por las iniciales
de tu primer nombre, la Y por la inicial de tu apellido paterno y la Z por la inicial de tu segundo
apellido.
7. Consulta los criterios de evaluación y verifica que tu actividad cumple con cada uno de ellos.
8. Entrega tu trabajo en la herramienta correspondiente dentro del aula virtual, de acuerdo al
calendario establecido en esta planeación
Ejercicios por resolver:
EJERCICIO 1.1
Una función es diferenciable en algún intervalo si la derivada existe en cada punto de dicho
intervalo. Una función diferenciable se llama también una función “suave”. En la Figura E1 se
muestran cuatro gráficas corresponden a funciones continuas en todo su dominio, indica cuáles
gráficas (señaladas como a,b,c ó d) corresponden a funciones diferenciables en la parte de su
dominio que se puede apreciar.
Figura E1: Las funciones graficadas son: (a) 𝑓(𝑥) = 𝑐𝑜𝑠(𝑥)/𝑥 , (b) 𝑓(𝑥) = |𝑥| − 3, (c) 𝑓(𝑥) =
|𝑥| − 2|𝑥 − 1| y (d) 𝑓(𝑥) = 𝑥 − 3 𝑠𝑖𝑛(𝑥). Gráficas elaboradas con Demos (2011).
Pág. 23
Módulo. Calculo Diferencial
Unidad 3
EJERCICIO 1.2
La siguiente figura (Figura E2) muestra parte de la gráfica de la función 𝑓(𝑥) = 4𝑥 3 + 3𝑥 2 − 6 𝑥 +
1, los puntos rojos son marcas en puntos de la gráfica que indican puntos bajo consideración. En
el contexto de la optimización de una función, selecciona la respuesta que indica qué tipo de
puntos son los marcados en rojo.
Figura E2: Función graficada 𝑓(𝑥) = 4𝑥 3 + 3𝑥 2 − 6 𝑥 + 1. Gráfica elaborada con Desmos(2011).
(a) 1-mínimo local, 2-máximo local, 3-mínimo local
(b) 1-máximo relativo, 2-punto de inflexión, 3-mínimo relativo.
(c) 1-punto de inflexión, 2-punto de inflexión, 3-mínimo relativo.
(d) 1-máximo global, 2-mínimo relativo, 3-punto de inflexión.
Pág. 24
Módulo. Calculo Diferencial
Unidad 3
EJERCICIO 2. De entre todos los rectángulos con diagonal dada, determinar aquel con que tiene
mayor área. Sugerencias: defina 𝑥, 𝑦 como las longitudes (mts.) de dos lados (distintos) del
rectángulo. (1) Considere, por el teorema de Pitágoras, que 𝐷 2 = 𝑥 2 + 𝑦 2 (D es la diagonal del
rectángulo, por definición un número positivo) y 𝐴(𝑥) = 𝑥𝑦 = 𝑥√(𝐷 2 − 𝑥 2 ) (la función de área del
rectángulo), (2) optimice 𝐴(𝑥) determinando sus puntos críticos, por último (3) 𝑥, 𝑦, y con base a
los criterios de la derivada o segunda derivada determine la naturaleza del punto crítico para x.
EJERCICIO 3.
Selecciona la respuesta correcta, agregando una marca a una de las cuatro opciones, por
ejemplo, marcando su respuesta en el inciso correspondiente en color amarillo.
3.1.- La notación diferencial de Leibniz para la derivada 𝒇′(𝒙) es:
(a)
𝑑𝑓(𝑥)
𝑑𝑥
(b) 𝑑𝑓(𝑥)
(c) 𝑑𝑓(𝑥)
(d) 𝑓̇ (𝑥)
3.2.- La definición de la derivada 𝒇′(𝒙) en términos de límite es:
(a) lim
ℎ→0
𝑓(𝑥+ℎ)−𝑓(𝑥)
ℎ
(c) lim
ℎ→0
(b) lim
ℎ→0
𝑓(ℎ)−𝑓(𝑥)
ℎ
𝑓(𝑥+ℎ)−𝑓(𝑥)
𝑓(𝑥)−ℎ
(d) lim 𝑓(𝑥 + ℎ) − 𝑓(𝑥)
ℎ→0
3.3.- ¿Es derivable la función 𝑓(𝑥) = |𝑥| en todo su dominio?
(a) Es derivable en todo su dominio (b) No es derivable en ningún punto (c) Es derivable en
todo su dominio excepto en el punto 𝑥 = 0.
(d) Solo es derivable en el punto 𝑥 = 0.
1
3.4.- La derivada de la función 𝑓(𝑥) = 𝑥 es:
(a)
1
𝑥2
1
(b) 𝑥 3
(c)
−1
𝑥2
1
(d) 2𝑥
1
3.5.- La derivada de la función 𝑓(𝑥) = 𝐼𝑛(𝑥) es:
Pág. 25
Módulo. Calculo Diferencial
(a)
Unidad 3
1
𝑥
(b)
−1
𝑥
3.6.- La regla (teorema) para determinar
(c)
𝑑𝑓(𝑥)𝑔(𝑥)
𝑑𝑥
−1
𝑥2
𝑥
(d) −2
el producto de dos funciones derivables
𝑓(𝑥), 𝑔(𝑥) en cualquier punto 𝒙 es :
(a)
𝑑𝑓(𝑥) 𝑑𝑔(𝑥)
/ 𝑑𝑥
𝑑𝑥
(c)
(b)
𝑑𝑓(𝑥)
𝑑𝑔(𝑥)
/𝑔(𝑥) + 𝑑𝑥 /𝑓(𝑥)
𝑑𝑥
3.7.- La regla (teorema) para determinar
𝑑𝑓(𝑥)
𝑑𝑔(𝑥)
𝑔(𝑥) + 𝑑𝑥 𝑓(𝑥)
𝑑𝑥
(d)
𝑑𝑓(𝑥)/𝑔(𝑥)
𝑑𝑥
𝑑𝑓(𝑥) 𝑑𝑔(𝑥)
𝑑𝑥
𝑑𝑥
, el cociente de dos funciones derivables
𝑓(𝑥), 𝑔(𝑥) en cualquier punto 𝒙, es:
(a)
𝑑𝑓(𝑥)/𝑑𝑥+𝑑𝑔(𝑥)/𝑑𝑥
𝑓(𝑥)2
(c)
𝑑𝑓(𝑥)
/𝑔(𝑥)2
𝑑𝑥
+
(b) [
𝑑𝑔(𝑥)
/𝑓(𝑥)2
𝑑𝑥
(d)
𝑑𝑓(𝑥)
𝑑𝑔(𝑥)
𝑔(𝑥) − 𝑑𝑥 𝑓(𝑥)] /𝑓(𝑥)2
𝑑𝑥
𝑑𝑓(𝑥)/𝑑𝑥 𝑑𝑔(𝑥)/𝑑𝑥
𝑓(𝑥)2
3.8.- La composición (𝑓 ∘ 𝑔)(𝑥) = 𝑓(𝑔(𝑥)) de las funciones 𝑓(𝑥) = √𝑥, 𝑔(𝑥) = cos(1 − 𝑥) es:
(a) √cos(1 − 𝑥)
(b) cos(1 − √𝑥)
(c) √cos(1 − √𝑥
(d) √1 − 𝑥
3.9.- La regla (teorema conocido como la regla de la cadena) para determinar
𝑑𝑓∘𝑔(𝑥)
𝑑𝑥
la
composición de dos funciones 𝑓(𝑥), 𝑔(𝑥), 𝑓(𝑥) derivable en el punto 𝑔(𝑥), y 𝑔(𝑥) derivable
en 𝑥, es :
(a)
𝑑𝑓(𝑔(𝑥)) 𝑑𝑔(𝑥)
𝑑𝑥
𝑑𝑥
(c)
𝑑𝑓(𝑥)
𝑑𝑔(𝑥)
+
𝑑𝑥
𝑑𝑥
(b)
𝑑𝑓(𝑥)
𝑑𝑔(𝑥)
𝑔(𝑥) + 𝑑𝑥 𝑓(𝑥)
𝑑𝑥
(d)
𝑑𝑓(𝑥) 𝑑𝑔(𝑥)
𝑑𝑥
𝑑𝑥
3.10.- La derivada de la composición (𝑔 ∘ 𝑓)(𝑥) = 𝑔(𝑓(𝑥)) de las funciones 𝑓(𝑥) = √𝑥, 𝑔(𝑥) =
cos(1 − 𝑥) es:
Pág. 26
Módulo. Calculo Diferencial
(a)
Unidad 3
𝒔𝒆𝒏(𝟏−𝒙)
(b) 𝒔𝒆𝒏(𝟏 − √𝑥)
𝟐√cos(1−𝑥)
(c) 𝒔𝒆𝒏(𝟏 − 𝑥) 2
1
√𝑥
1
2√𝑥
1
(d) 𝒔𝒆𝒏(𝟏 − √𝑥) 2𝑥
EJERCICIO 4.
La siguiente tabla contiene dos columnas, la primera columna numerada 1,2,3,4,5,6,7,8 y
la segunda a,b,c,d,e,f,g,h. Determina el emparejamiento solución el cual relaciona las
afirmaciones en la primer columna con las de la segunda columna. El emparejamiento
solución es biyectivo y es un conjunto de respuestas codificadas como {(𝒙, 𝒚) ∶ 𝒙 =
𝟏, … , 𝟖, 𝒚 = 𝒂, 𝒃, … , 𝒉}. El emparejamiento lo puedes indicar colocando en cada celda de la
primer columna su correspondiente pareja.
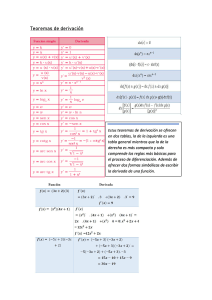
[1]
Esta
función
continua
esta
caracterizada de manera única por
𝒇(𝟎) = 𝟏 y 𝒇′(𝒙) = 𝒇(𝒙)
[2]
Función que corresponde a la
derivada de la función 𝒇(𝒙) = 𝒂𝒙 , 𝒂 ∈
(𝟎, ∞)
[3]
Si dos líneas que se intersectan en un
punto son cortadas por líneas
paralelas, los segmentos de línea
que se forman en una de la líneas
son
proporcionales
a
los
correspondientes
segmentos
formados en otra línea.
[4]
Aplicando el teorema de L’Hopital
podemos
comprobar
que
𝐥𝐢𝐦 𝒔𝒆𝒏(𝒙)/𝒙 es:
.
[𝒂]
(−𝟏)𝟑 𝒄𝒐𝒔(𝒙)
[𝒃]
Un ejemplo de diferenciación
simbólica. Un método para la
obtener las derivadas de una
función mediante el software.
[𝒄]
𝟏 − 𝒚𝟐 − 𝟐𝒙𝒚
𝒙𝟐 + 𝟐𝒙𝒚
[𝒅]
𝒈(𝒙) = 𝒂𝒙 𝑰𝒏(𝒂)
𝒙→𝟎
[𝒆]
[5]
𝒇(𝒙) = 𝒆𝒙
𝒔𝒆𝒏(𝒙), 𝒄𝒐𝒔(𝒙)
[6]
𝒅𝒊𝒇𝒇(𝒔𝒆𝒏(𝒙), 𝒙, 𝟐) = −𝒔𝒆𝒏(𝒙)
[𝟕]
𝑺𝒊 𝒚(𝒙) = 𝒄𝒐𝒔(𝒙), 𝒆𝒏𝒕𝒐𝒏𝒄𝒆𝒔 𝒚(𝟔) =
[𝟖]
𝑺𝒊 𝒙𝟐 𝒚 + 𝒙𝒚𝟐 = 𝒙, 𝒆𝒏𝒕𝒐𝒏𝒄𝒆𝒔
𝒅𝒚
𝒅𝒙
=
[𝟗]
Cuál es la función inversa de la
restricción
de
𝒇(𝒙) =
𝒙𝟐 𝒄𝒐𝒏 𝒅𝒐𝒎𝒊𝒏𝒊𝒐[𝟎, ∞) 𝒆 𝒊𝒎𝒂𝒈𝒆𝒏
[𝟎, ∞)
[𝒇]
Se conocen como las funciones
circulares fundamentales
[𝒈]
𝒄𝒐𝒔(𝟎)/𝟏
[𝒉]
Teorema de Thales de Mileto (sobre
triángulos semejantes)
[𝒊]
𝒈(𝒙) = 𝒙𝟏/𝟐
Pág. 27
Módulo. Calculo Diferencial
Unidad 3
Producto por entregar:
Documento en formato WORD que colocará el estudiante como tarea Evidencia de Aprendizaje
de la unidad 3, y subirá a la plataforma bajo la siguiente estructura: (1) Portada con datos de la
asignatura y estudiante (2) Contenido: respuestas a los ejercicios resueltos planteados con el
desarrollo incluido (3). Conclusión (4). Fuentes de consulta en formato APA.
Instrumento de evaluación
Escala de evaluación. Evidencia de Aprendizaje. Aplicación de la derivada.
Asignatura: Cálculo Diferencial
Semestre:
1
Unidad:
Unidad 3 Derivación
Actividad:
Actividad Evidencia de Aprendizaje – Aplicación de la derivada
Instrucciones: Anote en cada casilla los puntos obtenidos por el (la) estudiante en cada criterio
por evaluar.
Puntaje
por criterio
Criterios de evaluación
Puntaje
obtenido
Formato del documento
1. El documento en Word incluye portada, índice,
introducción, el desarrollo, conclusiones y referencia de
la bibliografía y del software utilizado en formato APA.
5
2. Desarrollo / contenido
3. El ejercicio 1 es resuelto total y correctamente
seleccionando las respuestas correctas a las dos
preguntas en los subejercicios 1.1 y 1.2.
4. El ejercicio 2 es planteado y resuelto total y
correctamente siguiendo las instrucciones y las
sugerencias.
5. El ejercicio 3 es resuelto total y correctamente bajo las
instrucciones.
Indicando
las
10
respuestas
correctamente.
6. El ejercicio 4 es resuelto total y correctamente bajo las
instrucciones. Determinando el emparejamiento
solución con nueve parejas (x,y) x=1,…,9, y=a,…i.
7. Conclusión
20
25
25
20
5
8. Incluye una conclusión de la actividad
Puntaje total
100
Pág. 28
Módulo. Calculo Diferencial
Unidad 3
Fuentes de Consulta:
Desmos (2011) [Software] Disponible en https://www.desmos.com/about?lang=es . Información:
https://es.wikipedia.org/wiki/Desmos_(herramienta_gr%C3%A1fica)
Purcell E. J., Varberg D., Rigdon S. E. (2007). Cálculo diferencial e integral, Pearson
Educación México, novena edición. Traducción de “Calculus, 9e by Dale Varberg, Edwin
J. Purcell and Steven E. Rigdon published by Pearson Education, Inc., publishing as
PRENTICE HALL, INC., 2007” por Victor Hugo Ibarra Mercado. Disponible en
https://www.cimat.mx/ciencia_para_jovenes/bachillerato/libros/[Purcell,Varberg,Rigdon]
Calculo/[Purcell,Varberg,Rigdon]Calculo.pdf
Spivak, M. (2008), Calculus, 4th edition, Publish or Perish.
http://valle.fciencias.unam.mx/licenciatura/bibliografia/spivak.pdf
Disponible en
Pág. 29