La transformada de Laplace

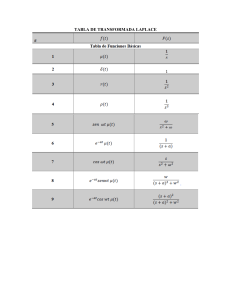
Tema 4:
Transformada de Laplace
Cálculo II
(Grado en Ingeniería en Diseño Industrial y
Desarrollo de Productos)
Departamento de Matemáticas
Índice
1. Introducción.
2. La Transformada de Laplace. Condiciones de
existencia. Propiedades.
3. Transformadas de funciones elementales.
Transformada de una derivada. Transformada
de una integral. Tabla de transformadas.
4. Aplicaciones:
4.1 Aplicaciones al Cálculo Integral.
4.2 Aplicaciones a la resolución de Ecuaciones
Diferenciales Ordinarias (EDO).
Introducción
• Los métodos de la Transformada de Laplace
tienen un papel clave en el enfoque moderno del
análisis y diseño en los sistemas de ingeniería.
• El incentivo para desarrollar estos métodos fue
el trabajo pionero del ingeniero electricista inglés
Oliver Heaviside (1850-1925) que desarrolló un
método para la solución sistemática de
ecuaciones diferenciales ordinarias con
coeficientes constantes.
• Debido a que trabajó en la práctica, su método
fue ampliamente aceptado por los ingenieros.
Introducción
• A principios del siglo XX, la Transformada de
Laplace se convertía en una herramienta común
en la teoría de vibraciones y la teoría de
circuitos, dos de los campos en los que ha sido
aplicada con mayor éxito.
• El estudio de la Transformada de Laplace dio
lugar a un capítulo de la Matemática llamado
Cálculo Operacional.
Transformada de Laplace
Sea f (t) una función definida en el intervalo [0,).
Se llama transformada de Laplace de la función f (t)
a la función:

L f t   F  p    e pt f t dt, p  
0
Dominio Dominio
de
de
tiempo frecuencia
Se dice que f (t) es una función de orden exponencial
 cuando t   si existen las constantes reales k y T
tales que para todo valor de t  T se verifica que:
sennt, tn, ent, ...
f t   k e t  lim
t 
f t 
0
t
e
Transformada de Laplace
Teorema.- Si f (t) es una función continua a
tramos en cada intervalo finito [0,T] y es de
orden exponencial  cuando t  , entonces
existe la Transformada de Laplace de la
función para todo valor de p > .
El teorema da una condición suficiente pero no
necesaria: puede existir la Transformada de
Laplace de una función a pesar de que las
condiciones del Teorema no se satisfagan.
Propiedades
Propiedad lineal: La f t   b g t   a L f t   bL g t 
Primer teorema de traslación o desplazamiento de
la frecuencia:


Si L f t   F  p  entonces L eat f t   F  p  a 
Segundo teorema de traslación o desplazamiento
temporal:
 f t  a , t  a
Si L f t   F  p  y g t   
0, t  a

entonces Lg t   e ap F  p 
Propiedades
Cambio de escala:
1  p
Si L f t   F  p  entonces L f kt   F  
k k
Comportamiento asintótico de F(p): Si f (t) es una
función continua a tramos en cada intervalo finito
[0,T] y es de orden exponencial  cuando t  ,
entonces lim F  p   0
p
Transformadas
de funciones elementales
• Transformada de una constante:
Lk    e k dt  k 

 pt
0

0
e
e dt  k 

 pt
Consecuentemente: L1  1 p
t 

k


p  t 0 p
 pt
• Transformada de la función potencial: r  0
 
Lt
r
 
L tr

r    et t r 1dt
0


1
  e t dt  r 1  e u u r du 
0
0
p
r  1

pt  u  pdt  du

p r 1
r!
r
Sir  Nentonces L t  r 1
p
 pt r
 
Transformadas
de funciones elementales
• Transformada de la función exponencial: Si p > a,
 
 
 
t 
e

1
L e   e e dt   e
dt  k 


0
0
p

a

 t 0 p  a
• Transformada de las funciones trigonométricas
seno y coseno:
1
p  ia
p
a
iat
Le 
 2
 2
i 2
2
2
p  ia
p a
p a
p  a2
p

Lcosat   2
2

p

a

 Lcosat   iLsin at   
a
 Lsin at  
2
2

p

a

at
L eiat
  p  a t

 pt at

  p  a t
Transformadas
de funciones elementales
• Transformada de las funciones hiperbólicas
seno y coseno: Dado que cosh(at) = cos(iat) y
sinh(at) =  i sin(iat), obtenemos:
p
p

 Lcosh at   Lcosiat   p 2  ia 2  p 2  a 2


ia
a
 Lsinh at   L i sin iat   i
 2
2
2
2

p

a


p

ia

Transformada
de la función derivada
• Sea f (t) una función continua para t  0, de
orden exponencial  cuando t  , y
supongamos que f ’(t) existe y es continua a
tramos para t  0. Entonces la Transformada
de Laplace de la función derivada f ’(t) existe
para p > a y es:
L f t   pL f t   f 0
 
Si f (t) es continua en el origen, entonces f (0+)
= f (0). Pero si f (t) es discontinua en el origen,
hay que calcular f (0+) por la derecha de t = 0.
Transformada
de la función derivada
• Sea f (t) una función continua y con derivada f ’(t)
continua para t  0, ambas de orden exponencial
 cuando t  , y supongamos que f ’’(t) existe y
es continua a tramos para t  0. Entonces la
Transformada de Laplace de la función derivada
segunda f ’’(t) existe para p > a y es:
L f t   p 2 L f t   p f 0   f 0 
En condiciones similares se obtendría:


L f n  t   p n L f t    p n k f k 1 0 
n
k 1
Transformada de Laplace
• Transformada de la función integral:
t
1

Si L f t   F  p  entonces L  f u  du  F  p 
 0
 p
• Transformada del producto:
n
d
F  p
n
Si L f t   F  p  entonces L t f t    1
dp n


n
• Transformada del cociente:

 f t 
Si L f t   F  p  entonces L 
  F  p  dp

 t  p
Ejercicios
1. Hallar la Transformada de Laplace de las
siguientes funciones:
1. f1 t   e t
at r
6. f 6 t   e  at  e  bt  t
2. f 2 t   e cosbt 
7. f 7 t   t 3 2
3.
8. f 8 t    et u cos2u  du
at
4.
5.
f 3 t   e at sin bt 
f 4 t   t 2e3t
f 5 t   t sin at 
t
0
9. f 9 t   e 2 t sin 5t  cos3t 
 t2,0  t  2
10. f10 t   
3t  1, t  2
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Aplicación al Cálculo Integral
2. Resolver las siguientes integrales impropias de
primera especie:

1.  t e 2 t sin t dt
0

sin t
0 t dt
2 t
e
 e 8 t
3. 
dt
0
t
2.
4.
5.




0
0
t 3e t sin t dt
2
sin
t
t
e
dt
t
Usando Maxima
Otras propiedades
Teorema del valor inicial: Sea f (t) una función
continua en el intervalo (0, a], a finito, tal que su
derivada f ’(t) sea continua a tramos en [0, a], y
que tanto f (t) como f ’(t) sean de orden
exponencial  cuando t  . En tal caso:
Si lim f t   f 0  entonces lim pF  p   f 0 
t 0
p
Otras propiedades
• Transformada de una función periódica: Sea f (t)
una función continua a tramos y periódica en el
intervalo (0, ), de periodo T. Entonces:
1
L f t  
1  e  pT

T
0
e  pt f t  dt
3. Hallar la transformada de Laplace de la función
periódica:
t , 0  t  1
f t   
1, 1  t  3
Ejemplos
4. Hallar la transformada de Laplace de la función
de onda rectangular:
 A, 0  t  A
f t   
 A, A  t  2 A
5. Hallar la transformada de Laplace de la función
parte entera:
E t   i  1 si i  1  t  i,
i  1, 2, 3,...
NOTA :

 nen1 p 
n 1
1
1  e 
p 2
Transformada de la función de
Heaviside
En ingeniería es común encontrar funciones que
corresponden a estados de sí o no, o bien activo
o inactivo. Por ejemplo, una fuerza externa que
actúa sobre un sistema mecánico o una tensión
eléctrica aplicada a un circuito, puede tener que
suspenderse después de cierto tiempo.
Para tratar de forma efectiva con estas funciones
discontinuas conviene introducir una función
especial llamada función escalón unitario (a  0).
0, t  a
H t  a   
1, t  a
Transformada de la función de
Heaviside
Si a = 0, la función escalón unitario se reduce a:
H(t)
0, t  0
H t   
1, t  0
1
t
-1
Es una función continua a tramos en todo intervalo
finito y de orden exponencial  cuando t   por lo
que posee transformada de Laplace:
LH t  a    e  pt H t  a  dt  


0
a
t 
 pt
 ap


e
e
e  pt dt  


p
  p  t a
Transformada de la función de
Heaviside
• Una aplicación interesante de la función de
Heaviside radica en el segundo teorema de la
traslación, como se indica a continuación:
LH t  a  f t  a    e H t  a  f t  a dt   e pt f t  a dt


 pt
0
a
Cambio de variable: t  a = z  dt = dz
t=az=aa=0
LH t  a  f t  a    e

0
 p a  z 
f z dz  e
ap

Por lo tanto: LH t  a  f t  a   e ap L f t 

0
e pz f z dz
Teorema de convolución
• Se llama convolución de las funciones f (t) y g (t),
y se representa en la forma: f (t)  g (t), a la
integral:
t
f t  g t    f t  u  g u du
0
• Propiedades:
– Conmutativa: f  g = g  f
– Asociativa: f  (g  h) = (f  g)  h
– Distributiva: f  (g + h) = f  g + f  h
Si L f t   F  p  
 entonces : L f t   g t   F  p   G  p 
y Lg t   G  p 
Transformada inversa de
Laplace
Sea L[ f (t)] = F (p), decimos que f (t) es la
transformada inversa de Laplace de la función F (p)
y se escribe f (t) = L1[F (p)]
Propiedad lineal:
L1a F  p   b G p   a L1F  p   bL1 G p 
Primer teorema de traslación: L1F  p  a   eat f t 
Segundo teorema de traslación:


L1 e ap F  p   H t  a 
Cambio de escala:
1
L F kp 
k
1
t
f 
k
Transformada inversa de
Laplace
• Teorema de Lerch: Sean f y g continuas a
tramos en todo intervalo finito [0, T] y de orden
exponencial  cuando t  , tales que sus
respectivas transformadas de Laplace están
definidas y coinciden en (a, ), para algún a  .
Entonces f (t) = g (t) para todo t > 0 donde ambas
son continuas.
L[]
f (t)
t0
L1[]
F(p)
Lema de Watson
• Si la función f (t) es desarrollable en serie de
Taylor en un entorno del origen:

f t    an t n
n 1
entonces también lo es su transformada:

an n!
F  p    n 1
n 1 p
Ejercicios
6. Aplicar el teorema de convolución para hallar
las siguientes transformadas inversas:


p
a. L  2

2 2
  p  a  
1
2


p
1
b. L  2

2 2
  p  a  


1
c. L  3



p
p

1


1
Usando Maxima
Usando Maxima
Usando Maxima
Ejercicios
7. Hallar las siguientes transformadas inversas:
 3p 1 
a. L  2

p

6
p

13


1


2p  6
b. L 
2

2




p

1
p

1


1
2


5
p
8p  6
1
c. L 
2

2




p

3
p

2
p

2


Aplicación a la resolución de
E.D.O.
8. Resolver las ecuaciones diferenciales siguientes:
1. y   y  t con y 0  0
2. y   2 y  10 sin t con y 0  1
3. y   4 y   13 y  2 sin t con y 0  1, y 0  2
4. y   9 y  et con y 0  1, y 0  2
9. Resolver el sistema de EDO siguiente:
 x  3x  y   0

2 x   3 y   2 y  t
sabiendo que x (0) = y (0) = 0
Aplicación a la resolución de
E.D.O.
10. Resolver la ecuación integral:
y  6 y u du  sin t
t
0
11. Resolver la ecuación:
y  3 y  4 y u  du  2e5t
t
0
sabiendo que y (0) = 0
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
desolve(['diff(y,t)+y=t],[y(t)]);
desolve: can't handle this case.
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Usando Maxima
Bibliografía
Matemáticas avanzadas para ingeniería. Glyn
James et al. Pearson Educación, México
(2002), 2ª ed.
ISBN: 978-970-26-0209-5