Factores Integrantes Ecuaciones Lineal de Primer Orden Variación
Anuncio

Factores Integrantes
R
My − Nx
= p(x), entonces µ(x) = e
N
R
Nx − M y
Si
= p(y), entonces µ(y) = e
M
Si
p(x) dx
p(y) dy
Ecuaciones Lineal de Primer Orden
y=
1
µ(x)
y 0 + p(x) y = h(x)
Z
R
µ(x) h(x) dx + C , donde µ(x) = e
p(x) dx
Variación de Parámetros
yp (x) = u1 (x) y1 (x) + u2 (x) y2 (x) donde
Z
y1 (x) f (x)
y2 (x) f (x)
dx
y
u2 (x) = +
dx
u1 (x) = −
W (y1 , y2 )
W (y1 , y2 )
Z
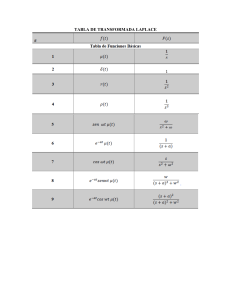
Transformada de Laplace
Fórmulas
Función
tn
↔ Transformada
n!
↔
sn+1
sen(a t)
↔
a
s2 +a2
senh(a t)
↔
a
s2 −a2
Ua (t) = U (t − a) ↔
e−a s
s
Función
ea t
↔ Transformada
1
↔
s−a
cos(a t)
↔
s
s2 +a2
cosh(a t) ↔
s
s2 −a2
Propiedades
Considere en estas propiedades que L {f (t)} = F (s) es la notación para la transformada de Laplace de la función f (t).
1. Linealidad: L {a f (t) + b g(t)} = a L {f (t)} + b L {g(t)}
2. Primer Teorema de Traslación: L {ea t f (t)} = F (s − a)
3. Teorema de la Transformada de la Derivada: L {f 0 (t)} = s F (s) − f (0)
4. L {f 00 (t)} = s2 F (s) − s f (0) − f 0 (0)
5. L {f (n) (t)} = sn F (s) − sn−1 f (0) − sn−2 f 0 (0) − . . . − f (n−1) (0)
dn
F (s)
dsn
Z T
1
7. Para f (t) función periódica (T es el periodo): L {f (t)} =
f (t) e−st dt
1 − e−sT 0
Z t
8. Convolución: L
f (σ) g(t − σ) dσ = F (s)G(s)
n
6. Teorema de la Derivada de la Transformada: L {tn f (t)} = (−1)
0
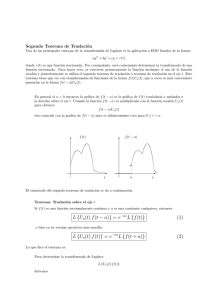
9. Versiones del segundo teorema de traslación: L {f (t − a) U (t − a)} = e−a s F (s) y L {f (t) U (t − a)} = e−a s L {f (t + a)}
1