L{Ua(t)f(t − a)} = e L{f(t)} (1) L{Ua(t)f(t)} = e L{f(t + a)} (2)

Segundo Teorema de Traslación
Una de las principales ventajas de la transformada de Laplace es la aplicación a EDO lineales de la forma:
ay 00 + by 0 + cy = r(t)
donde r(t) es una función seccionada. Por consiguiente, será conveniente determinar la transformada de una
función seccionada. Para hacer esto, se convierte primeramente la función mediante el uso de la función
escalón y posteriormente se utiliza el segundo teorema de traslación o teorema de traslación en el eje t. Este
teorema tiene que ver con transformadas de funciones de la forma f (t)Ua (t), que a veces es más conveniente
pensarlas en la forma f (t − a)Ua (t).
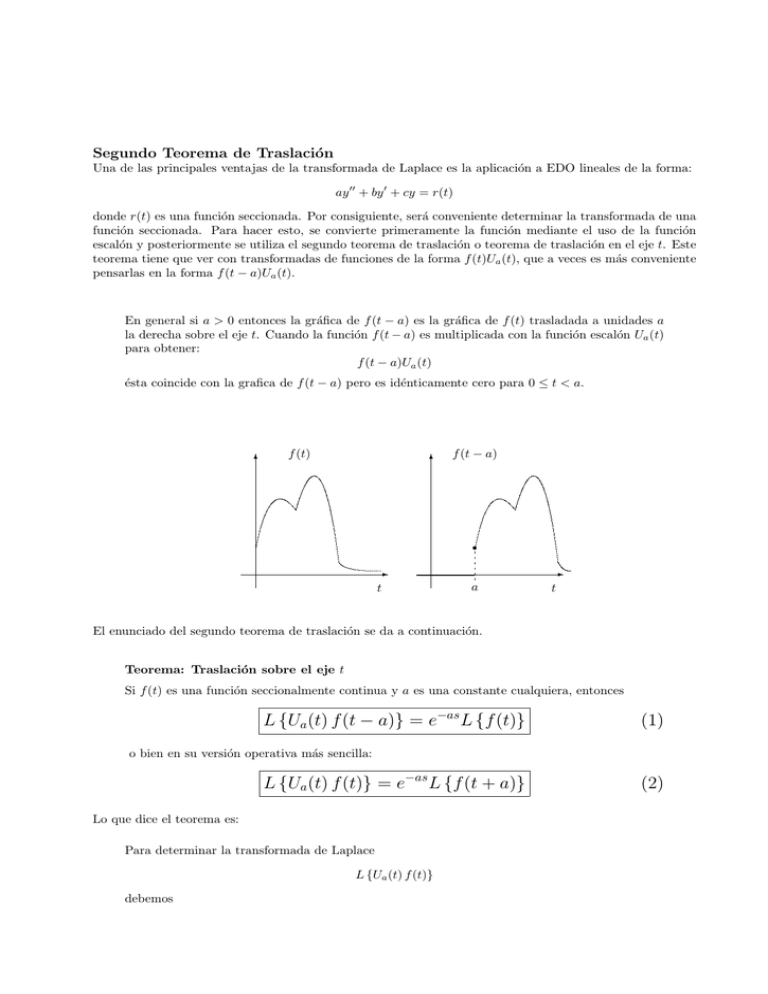
En general si a > 0 entonces la gráfica de f (t − a) es la gráfica de f (t) trasladada a unidades a
la derecha sobre el eje t. Cuando la función f (t − a) es multiplicada con la función escalón Ua (t)
para obtener:
f (t − a)Ua (t)
ésta coincide con la grafica de f (t − a) pero es idénticamente cero para 0 ≤ t < a.
f (t − a)
f (t)
6
6
r
t
a
t
El enunciado del segundo teorema de traslación se da a continuación.
Teorema: Traslación sobre el eje t
Si f (t) es una función seccionalmente continua y a es una constante cualquiera, entonces
L {Ua (t) f (t − a)} = e−as L {f (t)}
(1)
o bien en su versión operativa más sencilla:
L {Ua (t) f (t)} = e−as L {f (t + a)}
Lo que dice el teorema es:
Para determinar la transformada de Laplace
L {Ua (t) f (t)}
debemos
(2)
1. omitir el factor Ua (t),
2. cambiar todas las apariciones de t en f (t) por t + a (esto equivale a trasladar la función f (t)
a unidades a la izquierda en el eje t),
3. aplicar la transformada a la expresión resultante,
4. multiplicar el resultado por el factor e−a s
Este teorema tambien puede formularse para determinar la inversa de una expresión.
L−1 {e−as F (s)} = Ua (t)L−1 {F (s)}t→t−a
Ejemplos
1. Calcule la transformada de:
L {(3t + 1)U2 (t)}
Respuesta
De acuerdo con el segundo teorema de traslación:
L{(3t + 1) U2 (t)} = e−2s L{3(t + 2) + 1}
| {z } | {z }
|
{z
}
f (t)
Ua (t)
f (t+a)
= e−2s L {3t + 7}
= e−2s (3 L {t} + 7 L{1})
= e−2s 3 s12 + 7 1s
L {(3t + 1)U2 (t)} =
7
s
+
3
s2
e−2s
2. Calcule la transformada de la función cuya gráfica es:
6
f (t)
1
s
0
t
1
-1
Respuesta
Podemos conceptualizar a la función formada por 4 señales;
2
(3)
• 2 en el intervalo de tiempo [0, 2],
• -1 en el intervalo de tiempo [2, 3],
• t − 3 en el intervalo de tiempo [3, 4], y
• 1 en el intervalo de tiempo [4, +∞)
Ası́ la señal se puede realizar se convierte mediante la función escalón como:
f (t)
=
2 × (U0 (t) − U2 (t)) + −1 × (U2 (t) − U3 (t)) + (t − 3) × (U3 (t) − U4 (t)) + 1 × U4 (t)
f (t)
=
2 U0 (t) − 3 U2 (t) + (t − 2)U3 (t) + (−t + 2)U4 (t)
Por tanto:
L{f (t)} = L {2 U0 (t) − 3 U2 (t) + (t − 2) U3 (t) + (−t + 2) U4 (t)}
= L{2 U0 (t)} − L{ U2 (t)} + L{(t − 2) U3 (t)} + L{(−t + 2) U4 (t)}
= L{|{z}
2 U0 (t)} − L{|{z}
3 U2 (t)} + L{(t − 2) U3 (t)} + L{(−t + 2) U4 (t)}
| {z }
| {z }
f (t)
f (t)
f (t)
f (t)
= e−0 s L{2} − e−2 s L{3} + e−3 s L{(t + 3) − 2} + e−4 s L{−(t + 4) + 2}
Ası́:
=
1×
=
2
s
2
s
− e−2 s
− e−2 s
3
s
3
s
+ e−3 s L{t + 1} + e−4 s L{−t − 2}
+ e−3 s
1
s2
2 3
L{f (t)} = − e−2 s +
s s
1
s
+
+ e−4 s − s12 −
1
1
+
s2
s
−3 s
e
2
s
1
2
+ − 2−
s
s
e−4 s
Pasemos ahora a ilustra como se determina aplica el segundo teorema de traslación en el cálculo de transformadas inversas.
1. Calcule
L−1
e−πs
s2 + 4
Respuesta
De acuerdo a la fórmula 3,
L−1
n
e−πs
s2 +4
o
= Uπ (t) L−1 { s21+4 }t→t−π
= Uπ (t) 12 L−1 { s22+4 }t→t−π
= Uπ (t) 12 [sen(2t)]t→t−π
L−1
n
e−πs
s2 +4
o
=
1
2
Uπ (t) sen(2(t − π))
=
1
2
Uπ (t) sen(2t − 2π)
=
1
2
Uπ (t) sen(2t)
=
1
2
sen(2t) Uπ (t)
3