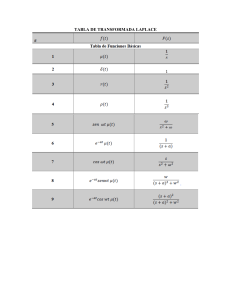
¼¼ ¼ ¼ ¼ e bz e a Ô
Anuncio

Facultad de F
sica, P. Universidad Cat
olica de Chile
FIZ{2510: M
etodos Matem
aticos de la F
sica I
Curso: R. Benguria, Semestre Primavera 2000
Tarea # 12
Fecha de Entrega: Jueves 23 de Noviembre, 2000
Encuentre las transformadas de Laplace y las regiones de convergencia en los ejercicios siguientes:
Problema 57:
g (t)
g (t)
= t2 sen(bt);
g (t)
= cos2 (bt);
g (t)
Problema 58:
= cosh(t);
= H (t
a)sen(bt):
Resuelva la ecuacion diferencial
y 00 (t) + y (t)
= t sent;
y (0)
= 0;
y 0 (0)
= 1;
utilizando transformadas de Laplace.
Problema 59:
Resuelva el sistema de ecuaciones diferenciales:
y 0 (t)
= y (t)
v (t) + sent;
v 0 (t) = y (t) + v (t) + et ;
con y (0) = 0, v (0) = 1.
Encuentre las inversas de las transformadas de Laplace que se
dan a continuacion. Suponga que cada transformada se dene en el semiplano
<(s) > a y b es real.
Problema 60:
1
;
(z + a)3
z
z3
+ a3
e bz
z (z 2
Problema 61:
;
:
+ a2 )
Resuelva la ecuacion de convolucion:
Z t
y (t) = 1 +
(t )y ( ) d:
0
Problema 62:
Invierta la transformada de Laplace siguiente:
p
e a z
pz
<(z ) > 0:
;
1