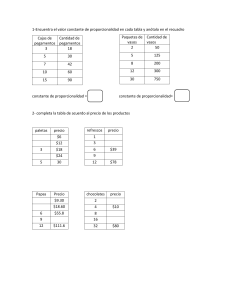
PROPORCIONALIDAD DIRECTA, INVERSA y COMPUESTA Problema 1: Hemos comprado 3kg de manzanas y nos han cobrado 3,45 € ¿Cuánto nos cobrarían por 1, 2 5 y 10 kg? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 1 Problema 2: Marta ha cobrado 126 € por repartir propaganda durante cinco días. ¿Cuántos días deberá trabajar para cobrar 340,2 €? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 2 Problema 3: En un plano de una ciudad, una calle de 350 metros de longitud mide 2,8 cm. ¿Cuánto medirá sobre ese mismo plano otra calle de 200 metros? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 3 Problema 4: En una panadería, con 80 kg de harina hacen 120 kg de pan. ¿Cuántos kilos de harina serían necesarios para hacer 99 kg de pan? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 4 Problema 5: Ana medía 1,42 m a principios de año. Pasados tres meses, medía 1,45 y a finales de año 1,51 ¿Cuándo creció más rápido, en los tres primeros meses o en el resto del año? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 5 Problema 6: En el equipo de fútbol del barrio han jugado como porteros Ángel y Diego. A Ángel le han marcado 13 goles en 10 partidos jugados. Diego jugó 15 partidos y le marcaron 18 goles ¿Cuál de los dos ha tenido mejores actuaciones? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 6 Problema 7: Una piscina portátil ha tardado en llenarse seis horas utilizando cuatro grifos iguales. ¿Cuántos grifos, iguales a los anteriores, serían necesarios para llenarla en 3 horas? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 7 Problema 8: Para construir una casa en ocho meses han sido necesarios seis albañiles. ¿Cuántos habrían sido necesarios para construir la casa en tan solo tres meses? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 8 Problema 9: En una fábrica automovilística, una máquina pone, en total, 15.000 tornillos en las 8 horas de jornada laboral, funcionando de forma ininterrumpida. ¿Cuántos tornillos pondrá en 3 horas? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 9 Problema 10: Después de una fuerte tormenta, dos autobombas han tardado 6 horas en desaguar un garaje que se había anegado. ¿Cuántas horas se hubieran tardado utilizando 3 autobombas? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 10 Problema 11: Un coche ha tardado 42 minutos en recorrer 70 km. Suponiendo que va a la misma velocidad, contesta a las siguientes cuestiones: 1.- ¿Cuánto tardará en recorrer 150 km? 2.- ¿Cuántos kilómetros recorrerá en dos horas y tres minutos? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 11 Problema 12: Un automóvil ha tardado en hacer el recorrido Madrid-Zaragoza tres horas y cuarto a una media de 100 km/h. ¿Cuánto tardará un autobús a una media de 90 km/h? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 12 Problema 13: En un partido de baloncesto un jugador A ha conseguido 12 canastas de 20 intentos, otro, B, 6 de 16, y un tercero, C, 15 de 25. ¿Qué porcentaje de acierto ha tenido cada uno de ellos? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 13 Problema 14: Diego tenía que resolver 20 problemas de matemáticas. 1. Si resolvió bien el 30% de los problemas, ¿cuántos hizo correctamente? 2. ¿Cuántos tendría que haber resuelto correctamente para que el porcentaje de problemas bien hecho hubiera sido el 85%? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 14 Problema 15: Si en cierta tienda tenían rebajas del 20% y me rebajaron un abrigo 150€, ¿qué precio tenía el abrigo? ¿Cuánto me cobraron? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 15 Problema 16: Con las últimas lluvias el agua de un pantano ha aumentado un 27%. Si el agua embalsada es de 431,8 hl, ¿cuánta agua tenía antes de las lluvias? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 16 Problema 17: He conseguido que me rebajaran la nevera un 18%, con lo que me ha costado 574 €. ¿Cuánto valía antes de la rebaja? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 17 Problema 18: Los padres de Marina y Pablo han repartido entre ellos 30 € en dos partes directamente proporcionales a sus años. Si Marina tiene 14 años y Pablo 6, ¿cuánto le ha correspondido a cada uno de ellos? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 18 Problema 19: Se ha encargado a un orfebre el diseño y la fabricación de un trofeo que ha de pesar 5 kg y ha de estar fabricado con una aleación que contenga tres partes de oro, tres partes de plata y dos de cobre. ¿Qué cantidad se necesita de cada metal? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 19 Problema 20: Luis, Juan y Sandra han repartido 6.000 octavillas de publicidad en los buzones de su barrio y, por ello, han cobrado 165 €. Si Luis ha repartido 1.500, Sandra 2.500 y Juan 2.000, ¿qué cantidad de lo cobrado corresponde a cada uno? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 20 Problema 21: Reparte 480 en partes inversamente proporcionales a 3 y 5 SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 21 Problema 22: Una fontanera ha acordado, con sus dos operarios, repartir una gratificación de 340€ en partes inversamente proporcionales a sus sueldos. Si sus sueldos son 1.200€ y 1.350€ respectivamente, ¿cuánto le corresponderá a cada operario? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 22 Problema 23: Un padre reparte un premio de lotería de 9.300€ en proporción inversa a las edades de los hijos, que son 6, 8, 12 y 18 años. Halla lo que corresponde a cada hijo. SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 23 Problema 24: Una máquina embotelladora ha llenado 135 botellas en 15 minutos. ¿Cuántas botellas llenará en una hora y media? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 24 Problema 25: He recorrido 720 km en 9 horas a una velocidad media de 80 km/h. ¿Cuánto habría tardado si la velocidad media fuese 60 km/h? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 25 Problema 26: Por 3,5 kg de chirimoyas he pagado 6,3 €. ¿Cuánto pagaré por 5 kilos? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 26 Problema 27: Si 4 entradas de cine han costado 15,2€. ¿Cuánto costarán 5 entradas? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 27 Problema 28: Un corredor ha dado 8 vueltas a la pista en 12 minutos. ¿Cuántas vueltas dará, si se mantiene el mismo ritmo, en 18 minutos? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 28 Problema 29: Una población ha consumido 20.000 m3 de agua en 5 meses. ¿Cuántos m3 consumirá en un año? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 29 Problema 30: Un tren ha recorrido 240 km en tres horas. Si mantiene la misma velocidad, ¿cuántos km recorrerá en las próximas dos horas? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 30 Problema 31: Con 15 kg de alimentos se alimentan 5 personas durante 7 días. ¿Durante cuántos días se alimentarán 6 personas con 20 kg de alimento? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 31 Problema 32: Seis personas hacen 20 m de muro en 10 días. ¿Cuánto tardarán 8 personas en hacer 32 m de muro? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 32 Problema 33: Sabiendo que dispongo de 240€ y que con ellos puedo comprar 6 prendas a 40€ cada una. ¿Cuántas prendas puedo comprarme con 360€ si cada una me costase 30€? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 33 Problema 34: Por enviar un paquete de 5 kg de peso a una población que está a 60 km de distancia, una empresa de transporte me ha cobrado 9€. ¿Cuánto costará enviar un paquete de 15 kg a 200 km de distancia? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 34 Problema 35: Una cuadrilla de 8 mineros abre una galería de 120 m de longitud en 12 días-. Otra cuadrilla de 16 mineros, ¿cuántos metros de galería abrirán en 29 días? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 35 Problema 36: Si 30 máquinas fabrican 5.000 m de tejido en 20 días, ¿cuántas máquinas, iguales a las anteriores, será preciso poner en marcha para producir 7.000 m en 14 días? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 36 Problema 37: Un depósito de 500 L es llenado por un grifo de 5 cm2 de sección en 12 horas. ¿Cuánto tiempo tardará en llenarse un depósito de 750 L por un grifo de 8 cm2 de sección? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 37 Problema 38: Una instalación de alumbrado consta de 16 focos que funcionan 12 horas diarias durante 15 días, esto significa un consumo de 4,2 kw/h. ¿Cuánto consumirán 28 focos funcionando 14 horas al día durante tres semanas? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 38 Problema 39: En una residencia con 30 estudiantes, se gastan 18.000€ en 25 días. ¿Cuánto gastarán 42 estudiantes en 34 días, viviendo en idénticas condiciones? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 39 Problema 40: La alimentación de 12 animales durante 8 días cuesta 8.000€. ¿Cuánto costará la alimentación de 15 animales en 5 días? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 40 Problema 41: Si con 300 kg de algodón pueden trabajar 8 telares durante 2 días a razón de 6 horas diarias, ¿cuántos kg necesitarán 15 telares para trabajar 5 días a razón de 10 horas diarias? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 41 Problema 42: 25 farolas originan un gasto de 6.000 € al mes, estando encendidas 6 horas diarias. ¿Qué gasto originarían 5 farolas en 45 días, estando encendidas 8 horas diarias? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 42 Problema 43: Una persona desea hacer el Camino de Santiago a pie, para ello caminará 600 km en 25 días andando 4 horas por día. Si marcha 5 horas por día, ¿cuántos km recorrerá en 15 días? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 43 Problema 44: Una fábrica de muebles tarda 10 días con 6 carpinteros en hacer 30 armarios. Si tienen 20 días de plazo para entregar los 250 armarios de un hotel, ¿cuántos carpinteros necesitan? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 44 Problema 45: El precio de un espejo de 0,3 m de ancho y 0,24 m de largo es de 90€. ¿Qué anchura tendrá un espejo del mismo material de 0,36 m de largo que costó 126 €? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 45 Problema 46: Con 15 kg de alimentos comen 5 personas durante 12 días. ¿Durante cuántos días se alimentarán 6 personas con los mismos alimentos? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 46 Problema 47: Seis personas efectúan un trabajo en 10 días. ¿Cuánto tardarán 8 personas en hacer el mismo trabajo? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 47 Problema 48: Sabiendo que dispongo de una determinada cantidad de dinero y que con ella puedo comprar 6 prendas a 4.000€ cada una. ¿Cuántas me podría comprar si cada una costase 3.000€? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 48 Problema 49: Un ganadero tiene 20 vacas y dispone de pienso para alimentarlas durante 60 días. Si tuviese 120 vacas, ¿para cuántos días tendrá pienso? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 49 Problema 50: 8 obreros construyen una pared en 9 días. ¿Cuánto tardarán en hacerlo 6? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 50 Problema 51: 4 palas excavadoras hacen un trabajo de movimiento de tierras en 14 días. ¿Cuánto se tardará en hacer ese mismo trabajo si se dispusiese de 7 palas excavadoras? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 51 Problema 52: Un coche tarda 3 horas en recorrer un trayecto yendo a 90 km/h. ¿Cuánto tardará en recorrer el mismo trayecto yendo a 120 km/h? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 52 Problema 53: Un coche tarda, a 90 km/h, hace un recorrido en 5 horas. ¿Cuánto tiempo ganaría si hace el mismo trayecto aumentando su velocidad en 10 km/h? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 53 Problema 54: Un taller tarda en hacer un trabajo 8 días, otro taller B, tarda en hacer ese mismo trabajo 12 días, y un tercer taller C, tarda 24 días. ¿Cuántos días tardarían en hacer ese mismo trabajo, si trabajarán los tres talleres juntos? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 54 Problema 55: Dos grifos, de los cuales uno vierte 10 litros por minuto y el otro 8, han llenado un estanque de 600 litros. Sabiendo que el segundo ha estado funcionando 30 minutos más que el primero. ¿Cuánto tiempo han tardado en llenarlo? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 55 Problema 56: Dos grifos vierten agua en un estanque. El primero solo, lo llenaría en 5 horas, y el segundo en 6. ¿Cuántas horas emplearán en llenar juntos el estanque? SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 56 Problema 57: Si dos fracciones a/b y c/d son iguales, ¿qué se puede decir de la fracción siguiente? Razona la respuesta SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 57 Problema 58: Demuestra que si También se cumple que SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 58 Problema 59: Calcular las medidas de los ángulos de un triángulo, sabiendo que son inversamente proporcionales a 2, 3 y 5. SOLUCIÓN PROPORCIONALIDAD DIRECTA E INVERSA 59 Comparte si lo ves útil