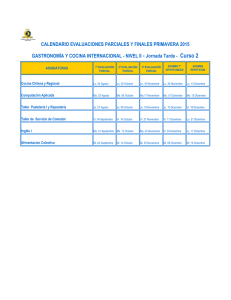
1. En un curso compuesto por 22 estudiantes; 12 estudian cocina tradicional; 11 estudian alta cocina y 11 cocina de vanguardia, 6 estudian cocina tradicional y alta cocina; 7 estudian alta cocina y cocina de vanguardia; 5 estudian cocina tradicional y de vanguardia y 2 estudian los tres cursos de cocina. CT 12 S = 22 CV 3 3 2 4 1 11 5 0 11 AC a) ¿Cuántos alumnos estudian sólo cocina de vanguardia? Respuesta: 1 b) ¿Cuántos alumnos estudian sólo cocina tradicional? Respuesta: 3 c) ¿Cuántos alumnos estudian solo alta cocina? Respuesta: 0 2. En una universidad el 60% de la población asiste al parque a hacer ejercicio y el 35% va al gimnasio. Si el 20% de la población va al parque y también al gimnasio ¿Qué porcentaje no va al ni parque ni al gimnasio? Respuesta: 25% S=1 GYM PARQUE 0.60 0.2 0.25 0.35 (𝑃 ∪ 𝐺)′ = 0.60 + 0.35 − 0.2 = 0.75 (𝑃 ∪ 𝐺)′ = 1 − 0.75 = 0.25 (𝑃 ∪ 𝐺)′ = 25% 3. Un jefe de publicidad ha entrevistado a 2000 personas para apreciar los efectos de 3 programas radiales. 580 personas escuchan el programa A, 840 el B, 920 el C, 260 el A y B, 220 el A y C, 300 el B y C y 100 el A, B, C. A B 580 200 𝑆 = 2000 840 160 380 100 120 200 500 340 920 C a) ¿Cuántas personas escuchan solo el A? ¿solo el B?, ¿solo el C? 𝐴 = 200, 𝐵 = 380, 𝐶 = 500 b) ¿Cuántas personas escuchaban solo A y B? ¿sólo A y C?, ¿sólo el B y C? 𝐴𝑦𝐵 = 160, 𝐴𝑦𝐶 = 120, 𝐵𝑦𝐶 = 200 c) ¿Cuántas personas escuchaban al menos un programa? 1660 d) ¿Cuántas no escuchaban ninguno de los 3? 340
