APUNTES. CAPÍTULO 1. CÓNICAS

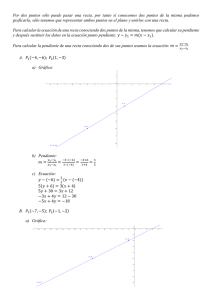
1
(Apuntes en revisión para orientar el aprendizaje)
CAPÍTULO 1 LAS CÓNICAS
INTRODUCCIÓN
DEFINICIÓN. Un lugar geométrico, en el plano " XY " , es aquel
espacio constituido por todos los puntos que satisfacen una
ecuación de la forma
f  x, y   0
Se trata de la gráfica que representa geométricamente a una
recta o a una curva cuyos puntos satisfacen una ecuación.
LA RECTA EN EL PLANO
Intuitivamente una recta es la menor distancia entre dos puntos
o una sucesión infinita de puntos en una misma dirección.
DEFINICIÓN. La recta es el lugar geométrico de todos los
puntos que satisfacen una ecuación del tipo
ax  by  c  0
A este tipo de ecuaciones se les conoce como lineales.
DEFINICIÓN. La pendiente de una recta o su inclinación,
denotada como " m " , es la tangente trigonométrica del ángulo
que forma dicha recta con el eje de las abscisas.
Esta pendiente puede ser nula, positiva, no existir o negativa.
y
m 0
m 0
m 
m 0
x
PABLO GARCÍA Y COLOMÉ
2
TEOREMA. Sean los puntos
A  x1, y1 
y
B  x2 , y2  del plano
" XY " . Entonces la inclinación de la recta que los une, esto es,
su pendiente, se calcula a través de:
y2  y1
m
x2  x1
Una verificación geométrica de este teorema se muestra en la
siguiente figura:
B  x2 , y2 
y
y2  y1
m  tan 
x2  x1

A  x1, y1 
x
Una definición más formal de la recta en el plano es:
DEFINICIÓN. Una recta es el lugar geométrico en el cual, para
dos cualesquiera de sus puntos
A  x1, y1 
y
B  x2 , y2  ;
x1  x2
la pendiente, siempre es constante.
Para dos puntos de la recta,
y
P  x, y  de coordenadas variables
P0  x0 , y0  de coordenadas constantes, de su pendiente se
puede obtener su ecuación como sigue:
PABLO GARCÍA Y COLOMÉ
3
m
y  y0
x  x0

y  y0  m  x  x0 
que es la forma punto-pendiente de la ecuación de la recta.
De la misma pendiente se deduce la forma conocida como
ecuación de la recta apoyada en dos puntos:
y2  y1
y  y1 
 x  x1 
x2  x1
Si en esta ecuación la pendiente es " m " y corta al eje " y " en
el punto B  0, b  donde a " b " se le conoce como ordenada
al origen y al eje " x " en el punto A  a, 0  donde a " a " se le
llama abscisa al origen, entonces, con B  0, b  y " m " , se llega
a la ecuación de la recta pendiente-ordenada al origen:
y  mx  b
y
B  0, b 
A  a, 0 
x
Y si se toman los dos puntos A y B y se aplica la ecuación
de la recta apoyada en ellos, se tiene que:
y0 
b0
x  a

0a

 ay  bx  ab

x y
 1
a b
que se conoce como ecuación simétrica de la recta.
PABLO GARCÍA Y COLOMÉ
4
FORMA GENERAL DE LA ECUACIÓN DE UNA RECTA
La forma general de la ecuación de una recta oblicua es:
Ax  By  C  0
Es evidente que si se despeja a la variable
y
"y"
se obtiene:
A
C
x
B
B
A
C
y la ordenada al origen es b   .
B
B
Si la recta pasa por el origen de coordenadas, C  0 , si es
paralela al eje de las abscisas, su ecuación es y  k  k   y
La pendiente es
m 
si es paralela al eje de las ordenadas, su ecuación es
x  k k .


PARALELISMO Y PERPENDICULARIDAD ENTRE RECTAS
Dos rectas son paralelas sí y sólo si sus pendientes son iguales y
son perpendiculares sí y sólo si sus pendientes son inversas y de
signo contrario.
y
y
900 1
1
2
paralelismo
m1  m2
x
x
2
perpendicularidad
m1  
1
m2
ÁNGULO ENTRE DOS RECTAS
PABLO GARCÍA Y COLOMÉ
5
x

2
1
x
El ángulo agudo  entre las dos rectas consideradas es igual a:
   2  1  tan  tan  2   
Y por la trigonometría:
tan  tan  2  1  
tan 2  tan1
1  tan 2  tan1 
Luego, el ángulo entre dos rectas se obtiene con:
m2  m1
  ang tan
1 m2 m1
El signo del cociente depende de a cuál recta se le asigna la
pendiente m1 y a cuál m 2 . En caso de ser negativo el
cociente, lo que se obtiene es el ángulo obtuso, pero si se
considera el valor absoluto del cociente, se tendrá
invariablemente el ángulo agudo.
DISTANCIA ENTRE UN PUNTO Y UNA RECTA
Sea una recta dada por su ecuación pendiente-ordenada al
origen y un punto P x0 , y0 .


PABLO GARCÍA Y COLOMÉ
6
y
P  x0 , y0 
y0
d
y0   mx0  b
 Q
mx0  b
m2  1
T
1
 R
y  mx  b
m
S
x0
x
Se define la distancia " d " entre el punto y la recta a la medida
sobre la línea perpendicular a la recta dada.
Sea la recta y  mx  b . Los catetos opuestos a los ángulos
"  " y la hipotenusa en los triángulos rectángulos PQR y RST ,
son, respectivamente:
PQ  d
y
PR  y0   mx0  b 
TS  1
La pendiente es
y TR  m2  1
A
C
m   y la ordenada al origen es b   .
B
B
De los triángulos y la trigonometría es posible escribir que:
sen  sen

d

d

y0   mx0  b 
1
m2  1
y0   mx0  b 
m2  1
PABLO GARCÍA Y COLOMÉ
7
 A 
 C 
y0     x0     
 B 
 B 
d
2
 A
  B  1


 d
Ax0  By0  C
Ejemplo. Dos rectas que se cortan en el punto
A2  B2
P  2,  1 tienen
como pendientes, respectivamente, los valores de
m1 
i)
1
2
y
m2  1
Obtener las ecuaciones de las rectas en su forma general y
en la forma pendiente-ordenada al origen.
ii) Determinar el ángulo agudo que estas rectas forman al
cortarse.
iii) Hacer un trazo aproximado de sus gráficas con su punto
de corte.
Solución.
PABLO GARCÍA Y COLOMÉ
8
Ejemplo. Determinar la ecuación de la recta en su forma
general si su ordenada al origen es 3 y se sabe además que es
paralela a la recta de ecuación 3 x  2y  12  0 . Calcular
también el ángulo agudo que esta recta forma con el eje de
las abscisas y graficarla de manera aproximada.
Solución.
PABLO GARCÍA Y COLOMÉ
9
Ejemplo. Sea la recta cuya ecuación general es
x  2y  6  0
i)
Obtener su ecuación pendiente-ordenada al origen y, con
ella, la pendiente de la recta.
ii) Determinar su ecuación simétrica, así como la abscisa y la
ordenada al origen. Considerar que en la abscisa y la
ordenada al origen se tienen los puntos de la recta de
coordenadas A a,0 y B 0, b respectivamente.

iii)



Con la pendiente de la recta calcular el ángulo agudo
que forma con el eje de las abscisas.
iv) Obtener el área del triángulo que la recta forma con los
ejes coordenados.
v) Calcular la distancia de la recta dada al origen y si esta
distancia constituye el segmento OE , obtener la ecuación
general de la recta sobre la cual se mide esta distancia, así
como su pendiente.
vi) Obtener la distancia de la recta dada en este ejemplo
con el punto
C  6,4  y si esta distancia constituye el segmento
CD , determinar la ecuación de la recta que lo contiene en su
forma general.
PABLO GARCÍA Y COLOMÉ
10
vii)
Calcular, utilizando funciones trigonométricas, el área de
los triángulos OEA y OEB y verificar que su suma es el
área pedida en el inciso
 iv  .
Solución.
PABLO GARCÍA Y COLOMÉ
11
LA CIRCUNFERENCIA
Se trata de una curva muy conocida. Los babilonios, excelentes
geómetras, dividieron el círculo zodiacal en 360 partes.
DEFINICIÓN. La circunferencia es el lugar geométrico en el
plano, formado por todos los puntos que equidistan de un punto
fijo conocido como centro.
Sea una circunferencia en el plano
y cuyo radio es
" XY "
con centro
" r " y sea un punto P  x, y  de ella.
C  h, k 
PABLO GARCÍA Y COLOMÉ
12
y
P  x, y 
r
C  h, k  Q  x, k 
x
En el triángulo CQP por Pitágoras, la hipotenusa " r " , que es el
radio de la circunferencia, se obtiene a partir de los catetos:
2
2
2
r  CQ  PQ
De donde:
2
CQ   x  h
y
PQ   y  k 
2

 x  h   y  k 
Luego
r 2   x  h   y  k 
2
2
2
2
2
2
 r2
que es la ecuación de la circunferencia con centro en el punto
C h, k y radio " r " .


Cuando el centro coincide con el origen, es evidente que
h  k  0 , por lo que su ecuación queda de la forma:
x2  y 2  r 2
y su gráfica entonces es como la de la siguiente figura:
PABLO GARCÍA Y COLOMÉ
13
y
x2  y 2  r 2
r
P  x, y 
x
C
FORMA GENERAL DE LA ECUACIÓN DE LA CIRCUNFERENCIA
Sea la ecuación de la circunferencia:
 x  h   y  k 
2
2
 r2
A partir de operaciones algebraicas y sustituciones se obtiene:
 x  h   y  k   r 2
2

2
 x 2  2 xh  h2  y 2  2yk  k2  r 2
x2  y 2   2h x   2k  y  h2  k2  r 2  0
Si se hace


D  2h ; E  2k ; F  h2  k2  r 2 :
x2  y 2  Dx  Ey  F  0
que es la ecuación de la circunferencia en su forma general.
Ejemplo. Obtener la ecuación de la circunferencia cuyo radio
es 3 y cuyo centro es la intersección entre las rectas cuyas
ecuaciones son:
x  2y  4  0
y
x  y  1 0
Hacer una gráfica del problema planteado.
PABLO GARCÍA Y COLOMÉ
14
Solución.
Ejemplo. Dada la ecuación general siguiente que representa
una circunferencia, determinar su centro, su radio y hacer un
trazo aproximado de su gráfica:
15
x  y  3 x  5y 
0
2
2
2
Solución.
PABLO GARCÍA Y COLOMÉ
15
Ejemplo. Dada la circunferencia de ecuación
 x  2
2
  y  3   20
2
determinar la ecuación de la recta tangente a esta curva que
pasa por el punto P 8, 3 . Hacer una gráfica del problema


pedido.
Solución.
PABLO GARCÍA Y COLOMÉ
16
Ejemplo. Obtener la ecuación de la circunferencia que pasa
por los puntos
 2, 2  ,  0, 2  2
 

3 y 2  2 3, 0 . Graficar
la curva y señalar los puntos.
Solución.
CÓNICAS
Antecedentes históricos. Menecmo (380 - 320 a.C.),
matemático y geómetra griego, discípulo de Platón y tutor de
Alejandro Magno, las descubrió y el matemático griego
Apolonio (262-190 A.C.) de Perga, quien primero las estudió al
considerar intersecciones entre un cono y un plano, llegó a la
interpretación geométrica de estas curvas, lo que se observa
en la siguiente figura:
PABLO GARCÍA Y COLOMÉ
17
Elipse
Parábola
Hipérbola
La palabra viene del latín ellipsis y esta voz del griego elleipsis
(falta). Esta curva cerrada, llamada elipse, debe su nombre al
ser una circunferencia imperfecta.
La palabra parábola viene del griego parabolé, comparación,
semejanza. Está formada por la palabra para, al margen y
bolé, arrojar, o sea, lanzar al margen de algo.
El término Hipérbole proviene del griego "hyperbole" que está
formada por el sufijo "hyper", sobre, por encima de y de "bole",
lanzamiento, arrojar, lanzar, por lo que el significado sería "tirar
encima".
Apolonio estudió muchas propiedades de estas curvas y
algunas de estas son utilizadas en la actualidad para definirlas.
Se cuenta que Arquímedes (287-212 A.C.), científico griego de
la antigüedad clásica, quemó los barcos romanos al defender
Siracusa con espejos parabólicos.
PABLO GARCÍA Y COLOMÉ
18
René Descartes (1596-1650), desarrolló la Geometría Analítica
para relacionar las curvas con ecuaciones. Y a Jan de Witt
(1629-1672), abogado y matemático holandés, se debe que
todas las ecuaciones de segundo grado en dos variables
representan secciones cónicas. Johannes Kepler (1570-1630)
descubrió que las órbitas de los planetas alrededor del sol son
elipses que tienen al sol como uno de sus focos y más tarde el
célebre matemático y físico inglés Isaac Newton (1642-1727)
probó que la órbita de un cuerpo alrededor de una fuerza de
tipo gravitatoria es siempre una cónica.
Hoy día se utilizan en las investigaciones espaciales y en el
comportamiento de partículas atómicas. Así, la hipérbola se
utiliza para describir la trayectoria de una partícula alfa en el
campo eléctrico producido por el núcleo de un átomo.
LA PARÁBOLA
DEFINICIÓN. La parábola es el conjunto de todos los puntos que
se mueven en un plano de tal forma que su distancia a una
recta fija (L) del plano llamada directriz, es siempre igual a su
distancia a un punto fijo del plano, que no pertenece a la recta
y que se conoce como foco (F).
Si F estuviera en L, la curva degeneraría en una recta.
Considérese entonces esta cónica, como la de la figura, donde
se señalan un punto de ella (A), el foco (F), el eje, la directriz
(L), un punto de esta (B) y el vértice de la curva (V).
PABLO GARCÍA Y COLOMÉ
19
A
eje
F V
B
directriz  L 
Para determinar una ecuación sencilla, se considerará una con
su eje sobre el eje de las ordenadas y su vértice en el origen y
a partir de ella se deducirá su ecuación. Entonces se tiene la
curva de la siguiente figura:
y
eje
F  0, p
D : y  p
P  x, y 
V
 x ', y '
x
P '  x,  p 
Por la condición establecida en la definición, se debe cumplir
que la distancia entre P y F es igual a la distancia entre
P y P ' , lo que se escribe como:
PABLO GARCÍA Y COLOMÉ
20
 x  0    y  p 
2
2
 x  x    y  p
2
2
Se elevan al cuadrado ambos miembros y se obtiene:
 x  0    y  p   x  x    y  p
2
2
2
2
 x2  4py
x2  y 2  2 py  p2  y 2  2py  p2
Esta es la ecuación canónica de la parábola con vértice
V  0, 0  ,
eje de simetría el de las ordenadas, que abre hacia
arriba y con
y  p como ecuación de su directriz (D).
Se llama lado recto de la parábola a la cuerda que forma parte
de la secante, horizontal o vertical, según sea el caso, que
pasa por el foco. En este caso, el lado recto es:
LR  2 x ' 

LR  2 4 py '
LR  2 4 p  p 

;
y'  p
LR  4 p
El lado recto 4p en todo los casos es el coeficiente de la
variable de primer grado de la ecuación. El radio vector o radio
focal de un punto P a su distancia al foco F .
Cuando la parábola abre hacia arriba p  0 y cuando abre
hacia abajo, p  0 ; en este caso, la ecuación de la cónica es:
x2  4py
y su gráfica es la siguiente, donde la directriz es
y  p:
PABLO GARCÍA Y COLOMÉ
21
y
D: y  p
P '  x, p 
V
x
P  x, y 
F  0,  p
eje
Si la parábola, con vértice en el origen, abre hacia la derecha
p  0 o hacia la izquierda p  0 , sus ecuaciones y




gráficas, respectivamente, son
y 2  4px
y
y 2  4px
Y sus gráficas:
y
P  x, y 
D : x  p
eje
V
F  p, 0 
x
y 2  4px
PABLO GARCÍA Y COLOMÉ
22
y
P  x, y 
eje
y 2  4px
F   p, 0 
P '  x, p 
V
x
D: x  p
Ahora considérese cuando el vértice no está en el origen. Por lo
pronto se verán únicamente los casos de parábolas cuando los
ejes son paralelos a uno de los ejes coordenados. Más
adelante se tratarán la traslación y la rotación de ejes y se hará
algún ejercicio que considere la traslación y la rotación de ejes
en alguna cónica.
Sea una parábola con vértice en V(h, k), donde h y k , son
las coordenadas del vértice. Aunque se verá el caso del vértice
en el primer cuadrante, es evidente que los resultados se
pueden extender a los otros tres cuadrantes.
PABLO GARCÍA Y COLOMÉ
23
y
F  h, k  p 
P  x, y 
D: y  k  p
P '  x, k  p
V  h, k 
x
eje
La distancia de P a F debe ser igual a la que hay entre
P y P ', luego se puede escribir:
 x  h  y   k  p   x  x   y   k  p
 x  h   y  k  p   x  x    y  k  p
2
2
2
x

h

y

k

p

y

k

p

 
 

2
2
2
2
2
2
2
2
x2  2 xh  h2  y 2  k2  p2  2ky  2py  2kp
 y 2  k2  p2  2ky  2py  2kp
2
2
x  2 xh  h  4py  4kp

 x  h
2
 4p  y  k 
Esta ecuación es la de la parábola con vértice en V(h, k) y
cuyo eje es paralelo al eje de las ordenadas. Es importante
hacer notar que en cualquier cuadrante se mantiene la forma
de la ecuación. Si la parábola ahora abre hacia abajo, con su
vértice en cualquier cuadrante, su ecuación, será de la forma:
PABLO GARCÍA Y COLOMÉ
24
 x  h  4p  y  k 
2
Y cuando el eje de la parábola es paralelo al eje de las
abscisas, en cualquier cuadrante que esté el vértice, cuando la
curva abre hacia la derecha, su ecuación es de la forma:
 y  k
2
 4p  x  h
Y si la parábola abre hacia la izquierda, su ecuación será de la
forma:
 y  k   4p  x  h
2
Se realizarán ahora algunos ejercicios sobre esta cónica:
Ejemplo. Determinar la ecuación de la parábola cuyo vértice
está en el origen y tiene su foco en el punto F 2,0 . Obtener


también las ecuaciones de su directriz y de su eje. Graficar.
Solución.
Ejemplo. Determinar la ecuación de la parábola con vértice en
el origen si la ecuación de la directriz es y  3 . Obtener
PABLO GARCÍA Y COLOMÉ
25
también las coordenadas del foco y la ecuación de su eje de
simetría. Graficar.
Solución.
Ejemplo. Determinar la ecuación de la parábola que tiene su
vértice en el origen, su eje en el eje de las ordenadas y que
pasa por el punto P 2, 1 . Dar la ecuación de su directriz, las


coordenadas de su foco, la longitud de su lado recto y hacer
un trazo aproximado de su gráfica.
Solución.
PABLO GARCÍA Y COLOMÉ
26
2
Ejemplo. Dada la ecuación y  2y  4 x  9  0 , que
representa a una parábola, expresarla en su forma canónica,
determinar las coordenadas de su vértice y foco, las
ecuaciones de su eje de simetría y de su directriz, y hacer un
trazo aproximado de su gráfica.
Solución.
PABLO GARCÍA Y COLOMÉ
27
Ejemplo. Obtener la ecuación de la parábola con vértice en el
punto V 2, 4 si su eje de simetría es la recta x  2 y pasa

por el punto

P  0, 2  . Graficar de manera aproximada y dar la
ecuación de su directriz y las coordenadas del foco.
Solución.
PABLO GARCÍA Y COLOMÉ
28
Ejemplo. Determinar la ecuación de la parábola que pasa por
los puntos A 0,0 , B 3,1 y C 8, 4 y cuyo eje es paralelo

  


al eje de las abscisas. Graficar de manera aproximada.
Solución.
PABLO GARCÍA Y COLOMÉ
29
LA ELIPSE
DEFINICIÓN. Es el conjunto de todos los puntos que se mueven
en un plano tales que la suma de sus respectivas distancias a
dos puntos fijos del mismo plano llamados focos F y F ' , es


una constante.
Una forma práctica para trazar una elipse, sin analizar cuál es
su ecuación y debida a su definición es la siguiente: se fijan dos
clavos en una tabla a una determinada distancia y se coloca
alrededor de ellos un hilo con los extremos unidos cuya
longitud, doblado a la mitad, sea mayor que la distancia entre
los clavos. Después se tensa el hilo con un lápiz de tal manera
que forme un triángulo con las distancias de los clavos al punto
de tensión y la distancia entre los clavos. Al mover el lápiz, sin
dejar de tensar el hilo, se dibuja una elipse cuyos focos son los
puntos donde están los clavos.
Se llamará eje focal a la recta que contiene a los focos
F y F ' , y donde esta recta corta a la curva, se definen los


vértices,
V y V ' , puntos que a su vez definen al eje mayor de
la cónica. Y, perpendicular a este, que pasa por el centro C , y
toca a la curva en dos puntos, está el eje menor. Cualquier
recta que toca dos puntos de la elipse y que pasa por un foco
se llama cuerda focal y cuando es perpendicular al eje mayor,
se conoce como lado recto LR . Se llaman radios vectores a las
rectas que van de un punto de la elipse P a los focos.
Ecuación de la elipse. Sea una elipse con su centro en el origen
y cuyo eje mayor coincide con el eje de las abscisas y el
menor con el de las ordenadas. Considérese la siguiente figura
PABLO GARCÍA Y COLOMÉ
30
donde se
constantes:
nombran
algunas
coordenadas
y
B
V '  a,0 
O
F '  c,0 
variables
y
P  x, y 
F  c,0 
V  a,0 
x
B'
De acuerdo con la definición, la suma de las distancias de un
punto P a los focos es una magnitud constante, es decir,
d  PF   d  PF '  constante
Si el punto P coincidiera con el vértice
condición sería como sigue:
V , es evidente que esta
d  PF   d  PF '  d VF   d VF '  2a
Luego, para cualquier punto
que:
P  x, y  de la elipse, se cumple
d  PF   d  PF '  2a
de donde, por la distancia entre dos puntos, se puede obtener
que:
 x  c   y  0    x  c   y  0   2a
2
2
2
 x  c  y   x  c  y 2  2a
2
2
2
2
Esta expresión se puede escribir como:
 x  c  y 2  2a 
2
 x  c  y 2
2
PABLO GARCÍA Y COLOMÉ
31
Se elevan al cuadrado ambos miembros y se realizan
operaciones algebraicas, de donde se obtiene que:
 x  c
 y 2  4a2  4a
 x  c
x2  2 xc  c2  y 2  4a2  4a
 x  c
2
a
2
2
 y 2   x  c  y 2
2
 y 2  x 2  2 xc  c2  y 2
 x  c  y 2  a2  xc
2
Se elevan ambos miembros al cuadrado y se obtiene:


a2 x2  2 xc  c2  y 2  a4  2a2 xc  x2c2
a2 x2  2a2 xc  a2c2  a2 y 2  a4  2a2 xc  x 2c2
a2 x2  a2 c2  a2 y 2  a4  x 2c2
a2 x 2  x 2 c2  a2 y 2  a4  a2 c2



x 2 a2  c2  a2 y 2  a2 a2  c2

Si se considera al triángulo isósceles de la figura, que se
obtiene de unir los focos de la elipse dada con el punto " B " es
evidente que cada uno de los lados iguales equivale a " a " y si
a la distancia del origen al punto " B " se le llama " b " se tiene
la figura siguiente:
B
a
F'
a
b
c O c
F
En cualquiera de los dos triángulos rectángulos se observa que
a2  c2  b2 , luego,
2
2
2
2
2
2
x b a y a b
x2 y 2

 2 1
2
a
b
PABLO GARCÍA Y COLOMÉ
32
que es la ecuación de la elipse con centro en el origen y ejes:
el mayor que coincide con el eje de las abscisas y el menor
con el de las ordenadas.
Es sencillo ver que en este caso la elipse es simétrica con
respecto a ambos ejes coordenados y que se trata de una
curva cerrada, que no es el caso de la parábola.
Considérese la misma elipse dada, pero ahora con el punto
P x, y que se ubica en la intersección de la recta vertical que


pasa por el foco
F  c,0  y la curva:
y
B
V'
P
O
F'
F
V x
P'
B'
Como se sabe, d  PF   d  PF '  2a y del triángulo PFF ' se
LR
tiene que d  PF  
, luego, por el teorema de Pitágoras:
2
2
2
2
2
LR
LR
LR
 
  

2
2



d
PF
'

4
c


2
a


4
c


 2 
 2  


2 
 
  
2
2
 LR 
 LR 
2
2

4
a

2
aLR

 2 
 2   4c
 
 

2aLR  4a2  4c2
PABLO GARCÍA Y COLOMÉ
33
LR 

2 a2  c2


a
2b2
LR 
a
que corresponde a la longitud del lado recto de la elipse.
Otro de los elementos de la elipse es la excentricidad, palabra
que viene de excéntrico (fuera del centro) que se denota con
" e " y que se define como el cociente de la distancia del
centro al foco, entre el semieje mayor, esto es,
c
e
a

a2  b2
e
a
; ca 
e 1
La excentricidad es un parámetro que determina el grado de
desviación de la elipse, con respecto a una circunferencia.
Considérese ahora el caso en que el eje mayor coincide con el
eje de las ordenadas y el centro de la elipse está en el origen:
y
V  0, a
F  0, c
B '  b,0 
O
B  b,0 
x
F '  0, c
V '  0, a
PABLO GARCÍA Y COLOMÉ
34
En este caso, de la misma forma que con anterioridad, a través
de la condición geométrica de esta cónica, se llega a su
ecuación que está dada por:
x2 y 2
 2 1
2
b
a
Aquí también se tiene que:
2b2
LR 
a
c
a2  b2
e 
1
a
a
y
En el caso en que esta cónica tuviera su centro en un punto
C  h, k 
diferente al origen y su eje focal fuera paralelo al eje
de las abscisas, entonces su ecuación sería de la forma:
 x  h
y  k


2
2
a
2
b
Y su gráfica sería la siguiente:
2
1
y
B
V'
P  x, y 
C  h, k  F
F'
V
B'
F '  h  c, k 
F  h  c, k 
x
Para obtener esta ecuación se acude a la condición y se
obtiene el siguiente desarrollo algebraico, del cual sólo se
mostrarán algunos pasos:
PABLO GARCÍA Y COLOMÉ
35
 x   h  c    y  k    x   h  c   y  k   2a
2
2
2
x2  2 x  h  c   h  c   y  k 
2
2
2
 2a  x 2  2 x  h  c    h  c    y  k 
2
Se elevan ambos
simplificaciones y,
miembros
al
cuadrado,
2
se
realizan
a2  xc  hc  a x2  2 xh  2 xc  h2  2hc  c2  y 2  2yk  k2
Se elevan otra vez los dos miembros al cuadrado, se efectúan
2
2
2
simplificaciones, se utiliza el hecho de que b  a  c y se
llega a la ecuación de esta elipse:







x2 a2  c2  h2 a2  c2  a2  y  k   a2 a2  c2  2xh a2  c2
2

x2 b2  h2 b2  a2  y  k   a2b2  2 xhb2
2
x b  2 xhb  h b  a  y  k   a2b2
2
2
2
2
2
b2  x  h  a2  y  k   a2b2 
2
2
2
2
 x  h
2
a
2
y  k

2
b
2
1
Si ahora el eje focal de la elipse es paralelo al eje de las
ordenadas y su centro se localiza en el punto
C  h, k  ,
entonces su ecuación es de la forma:
 x  h
2
b
2

 y  k
2
a
2
1
Y su gráfica es la siguiente:
PABLO GARCÍA Y COLOMÉ
36
y
V
F
B ' C  h, k 
B
x
O
F'
V'
Ahora se resolverán algunos ejercicios de esta cónica.
Ejemplo. Determinar la ecuación de la elipse cuyo centro está
en el origen de coordenadas, sus focos en los puntos
F 3, 0 y F ' 3, 0 y su gráfica corta al eje de las



abscisas en el punto

 5, 0  . Obtener también las coordenadas
de sus vértices, su lado recto y su excentricidad.
Solución.
PABLO GARCÍA Y COLOMÉ
37
Ejemplo. Dada la siguiente ecuación de una elipse, determinar
las coordenadas de sus vértices, de sus focos, su excentricidad,
la longitud de su lado recto y hacer un trazo aproximado de su
gráfica.
9x2  4y 2  36
Solución.
PABLO GARCÍA Y COLOMÉ
38
Ejemplo. Dada la siguiente ecuación general de una elipse, dar
las coordenadas del centro, vértices, focos, y las longitudes de
sus ejes mayor, menor, de cada lado recto y la excentricidad.
Graficar.
x2  4y 2  6x  16y  21  0
Solución.
PABLO GARCÍA Y COLOMÉ
39
Ejemplo. Se sabe que el centro de una elipse es el punto
C  2, 2  , su semieje menor es 3 , su excentricidad es
4
y su
5
eje focal es paralelo al eje de las ordenadas. Determinar su
ecuación ordinaria y general, así como las coordenadas de sus
vértices y focos. Graficar la cónica.
Solución.
PABLO GARCÍA Y COLOMÉ
40
LA HIPÉRBOLA
DEFINICIÓN. La hipérbola es el lugar geométrico de un punto
que se mueve en un plano tal que el valor absoluto de la
diferencia de sus distancias a dos puntos fijos, llamados focos,
se mantiene constante, evidentemente positiva, y menor que la
distancia entre los dos puntos fijos (focos).
y
P
B
L
F ' V 'C V F
L'
B'
x
La hipérbola, como puede verse en la figura, tiene dos ramas
de longitud infinita y dos ejes de simetría. El eje que pasa por
los focos es el eje focal y a la parte de él que une a los vértices
V y V ' se le denota eje transverso. En el centro de este eje
se localiza el centro de la hipérbola. Al eje que se encuentra en
ángulo recto con el eje transverso y que pasa a través del
centro de la hipérbola, se le llama eje normal o eje conjugado
(la parte que une a los puntos B y B '). A la distancia entre
L y L ', que es una cuerda focal y es perpendicular al eje
focal se le llama lado recto. Alas distancias entre los focos y un
punto P , esto es, los segmentos PF y PF ' se les llama
radios vectores de la curva.
PABLO GARCÍA Y COLOMÉ
41
Las coordenadas de los vértices son
las
de
B  0, b
F  c,0 
los
y
y
extremos
B '  0, b
del
las
y
V  a,0 
eje
de
V '  a,0  ,
y
conjugado
los
focos
son
son
F '  c,0  . Y, como se ve en la figura, las ramas
de esta cónica son asintóticas a las rectas que unen las
esquinas de un rectángulo formado por las referencias
paralelas a los ejes coordenados de los vértices y de los
extremos del eje conjugado.
ECUACIÓN DE LA HIPÉRBOLA. Sea una hipérbola como la de la
figura anterior con su eje transverso que coincide con el eje de
las abscisas, el conjugado con el eje de las ordenadas y el
centro con el origen.
y
P  x, y 
d2
F '  c,0 
B
d2
d1
V 'C V
Q
d1
F  c,0 
x
B'
De acuerdo a la definición se puede escribir que:
FP  F ' P  2a  constante 
PABLO GARCÍA Y COLOMÉ
42
Es evidente el resultado del valor absoluto de esta diferencia ya
que si por ejemplo se considera el punto V ' de la hipérbola y
se obtiene la diferencia de sus distancias a los focos se tiene
que:
FV '  F ' V '  2a
que es la distancia entre los dos vértices
V
2a  2c .
definición se cumple además que
y
V '. Por la
De la ecuación anterior, que define a la hipérbola, se obtienen
los dos resultados siguientes:
FP  F ' P  d1  d2  2a
 rama izquierda
FQ  F 'Q  d1  d2  2a
 rama derecha
Si se utiliza la distancia entre puntos es posible escribir que:
FP  d1 
 x  c
2
y
2
y
Lo mismo sucedería con el punto
F ' P  d2 
 x  c
2
 y2
Q.
Entonces la diferencia entre estas distancias es:
 x  c  y 2 
2
 x  c  y 2   2a
2
Se pasa un radical al segundo miembro y si se sigue el
procedimiento utilizado en la elipse mediante operaciones
algebraicas, se llega a:
c
2


 a2 x2  a2 y 2  a2 c2  a2

PABLO GARCÍA Y COLOMÉ
43
c  a, por lo que la diferencia
c2  a2 es positiva y se designará como c2  a2  b2 , de
Como se sabe
2a  2c
donde se obtiene:
c
2



 a2 x2  a2 y 2  a2 c2  a2

b2 x2  a2y 2  a2b2

a2 b2 y,
b2 x2 a2 y 2 a2 b2
x2 y 2
 2 2  2 2 
 2 1
2 2
2
ab
ab
ab
a
b
Se dividen ambos miembros entre
Esta es la ecuación simétrica de la hipérbola y se puede probar
que cualquier punto que satisfaga esta ecuación satisface
también la expresión que define a la cónica, esto es,
d1  d2  2a
Al analizar la ecuación de la hipérbola obtenida, se llega a:
x2 y 2
 2 1 ;
2
a
b
y0

x  a
De donde se prueba que la curva corta al eje de las abscisas
en los puntos donde se encuentran los vértices, esto es:
a,0 y a,0 .




Si se despejan ambas variables se llega a las expresiones
siguientes:
y
b 2
x  a2
a
y
x
a 2
y  b2
b
En la primera, si se considera uno de los dos signos para la
variable " y " , representa una función real de variable real y, de
acuerdo con el cálculo, su dominio se obtiene a partir de:
x2  a2  0  Df   , a  a,  
En este resultado se comprueba que entre los valores de
a y a , es decir, entre los vértices no hay curva y que
después de ellos, a la izquierda de
V ' y a la derecha de V , la
PABLO GARCÍA Y COLOMÉ
44
curva se extiende indefinidamente. De la expresión en que se
despejó a la variable " x " se obtiene que el recorrido de la
función, esto es, los valores que toma la variable " y " son todos
los reales, como se ve en las gráficas presentadas.
Para obtener el lado recto, se hace lo siguiente: basta con
obtener el doble del valor de la función, esto es, de la variable
" y " cuando la abscisa " x " toma el valor de la abscisa del
foco, es decir, cuando x  c . Así,
b 2
x  a2
a
b
y
b2
a
y

;

xc

b2
y
a
b 2
c  a2
a
2b 2
 LR 
a
y
Igual que para la elipse, la excentricidad es un parámetro que
determina el grado de desviación de la sección cónica, en
este caso la hipérbola, con respecto a una circunferencia y
expresa la razón entre la abscisa del foco y la del vértice, luego
se escribe como:
c
e   constante
a
Esto es equivalente a considerar, para cualquier punto
perteneciente a la hipérbola, la razón de su distancia a un foco
y su distancia a una recta fija llamada directriz. Aquí no se
estudiarán en los ejercicios de aplicación las directrices de la
hipérbola, pero el localizarlas equivale a externar la
excentricidad para el vértice " V " , de donde:
e
c ca

a ad
donde x  d es la ecuación de una directriz. La ecuación de
la otra sería
x  d
PABLO GARCÍA Y COLOMÉ
45
Entonces:
ca c

ad a

2
ac  a  ac  cd

a2
d
c
Luego las ecuaciones de las directrices de la hipérbola son:
a2
x
c
y
a2
x
c
Como c  a , la excentricidad en la hipérbola es siempre
mayor que la unidad.
Las ecuaciones de las asíntotas se determinan a través de:
y
b
x
a
Cuando el eje focal de la hipérbola coincide con el eje de las
ordenadas y su centro está en el origen, su ecuación es:
y 2 x2
 2 1
2
a
b
Su gráfica se muestra a continuación:
y
P
B'
F  0, c
V
O
V'
B
x
F '  0, c
PABLO GARCÍA Y COLOMÉ
46
También para esta hipérbola, la ordenada del vértice V es
" a " y la abscisa del punto B es " b " . La distancia " c " , que es
la ordenada del foco
F , equivale a c  a2  b2 , la longitud
2b2
LR 
a
del Lado Recto es
y la excentricidad está dada por
c
1
a
Si la hipérbola tiene su centro en C  h, k  y su eje focal es
e
paralelo al eje de las abscisas, entonces su ecuación es de la
forma:
 x  h
2
a
2

y  k
2
b
2
1
y su gráfica es la siguiente, donde se observa cómo la forma de
la curva se conserva y sólo cambia su posición en el plano
cartesiano. Las expresiones para la excentricidad y el lado
recto son las mismas.
y
P  x, y 
B
F' V ' V
B'
O
C  h, k 
F
x
PABLO GARCÍA Y COLOMÉ
47
C  h, k  y su eje focal es
Si la hipérbola tiene su centro en
paralelo al eje de las ordenadas, entonces su ecuación es de
la forma:
 y  k
2
a
2
x  h


2
2
b
1
y su gráfica es de la forma siguiente:
y
P
B'
F
V
C  h, k 
B
V'
O
F'
x
Ahora se resolverán algunos ejercicios de esta cónica.
Ejemplo. En una hipérbola, sus vértices y sus focos se localizan,
respectivamente, en los puntos cuyas coordenadas son:
V  0, 3  , V'  0,  3  , F  0, 5 
y
F '  0,  5 
Determinar: la ecuación de la cónica, las longitudes de sus ejes
conjugado y transverso, su excentricidad y la longitud de cada
lado recto. Graficar.
Solución.
PABLO GARCÍA Y COLOMÉ
48
Ejemplo. Sea la hipérbola cuya ecuación está dada por:
x2  4y 2  36
Determinar las coordenadas de sus vértices y de sus focos, la
longitud de sus ejes transverso y conjugado, la longitud del
lado recto, su excentricidad, las ecuaciones de sus asíntotas y
hacer un trazo aproximado de su gráfica.
Solución.
PABLO GARCÍA Y COLOMÉ
49
Ejemplo. Determinar en su forma simétrica y en su forma
general la ecuación de la hipérbola cuyos vértices son los
puntos V 2, 2
y V ' 2,  4 si se sabe que su lado




recto es " 2 " . Calcular las coordenadas del centro, de sus focos
y las longitudes de sus ejes transverso y conjugado, así como
las ecuaciones de sus asíntotas. Hacer una gráfica aproximada
de la cónica.
Solución.
PABLO GARCÍA Y COLOMÉ
50
Ejemplo. Dada la hipérbola cuya ecuación general es:
4 x2  25y 2  24 x  100y  164  0
Obtener su ecuación en su forma simétrica, determinar las
coordenadas de su centro, vértices y focos, la longitud de sus
ejes transverso y conjugado y del lado recto, calcular su
excentricidad y dar las ecuaciones de sus asíntotas y el ángulo
agudo de intersección entre ellas. Graficar de forma
aproximada.
Solución.
PABLO GARCÍA Y COLOMÉ
51
Ejemplo. Determinar las ecuaciones simétrica y general de la
hipérbola cuyo eje transverso es igual a " 4" si sus focos están
situados en los puntos de coordenadas:
F  3, 6 
;
F '  3, 0 
Obtener también las coordenadas de su centro y vértices, así
como las longitudes de su eje conjugado, de su lado recto, su
excentricidad y las ecuaciones de sus asíntotas. Hacer una
gráfica aproximada de esta cónica.
Solución.
PABLO GARCÍA Y COLOMÉ
52
TRANSFORMACIÓN DE COORDENADAS
DEFINICIÓN. Una transformación de coordenadas es un
procedimiento a través del cual, mediante determinadas
ecuaciones consideradas en un principio matemático, se
cambia una relación, una expresión o una figura, en otra cuyo
manejo resulta más sencillo, más fácil de manejar para un
determinado propósito.
TRASLACIÓN DE LOS EJES COORDENADOS
DEFINICIÓN. Al cambio de posición de los ejes coordenados en
el plano coordenado, a otro lugar del mismo, donde los nuevos
ejes sean paralelos a los originales y con el mismo sentido que
estos, se le conoce como traslación de ejes coordenados.
PABLO GARCÍA Y COLOMÉ
53
P  x, y  referido a un sistema coordenado XY
con origen de coordenadas en " O " , como se ve en la figura, y
Sea un punto
considérese también al mismo punto referido a otro sistema
X ' Y ' con origen en O ' h, k . Es evidente que las


coordenadas del punto, en este nuevo sistema serán diferentes
a las originales; se denotarán con P ' x ', y ' .

Y
Y'

 P  x, y 


P '  x ', y '
y
k
X'
O'
O

X
x
h
En la gráfica se ven con claridad los siguientes resultados:
x  x ' h
y
y  y ' k
Considérense los siguientes ejercicios:
Ejemplo. Transformar la siguiente ecuación de una curva
mediante la traslación de los ejes coordenados al punto
4,  2 . Trazar la curva con ambos sistemas coordenados.


y 3  x2  6y 2  8 x  12y  8  0
Solución. Se utilizan las expresiones anteriores que quedan
como:
x  x ' 4
y
y  y ' 2
Y al sustituirlas en la ecuación dada se obtiene:
 y ' 2    x ' 4 
3
2
 6  y ' 2   8  x ' 4   12  y ' 2   8  0
2
PABLO GARCÍA Y COLOMÉ
54
y '3  6y '2  12y ' 8  x '2  8 x ' 16  6y '2  24y ' 24  8 x ' 32  12y ' 24  8  0
y '3  x '2  0
 y '3  x '2
La gráfica de esta curva con respecto a ambos sistemas, se
muestra a continuación:
Y
Y'
O
O '  4, 2 
X
X'
En este ejemplo se observa cómo resulta mucho más sencillo
graficar en el nuevo sistema que en el original. Sería
conveniente para el lector, a manera de comprobación y para
lograr un mejor entendimiento de la transformación, graficar la
curva utilizando la ecuación original, para llegar a la misma
representación gráfica.
Lo usual es determinar el nuevo origen de coordenadas de tal
forma que se simplifique la ecuación y resulte más sencilla su
identificación y/o trazo con respecto al nuevo sistema
coordenado. Véase el siguiente ejemplo:
Ejemplo. Simplificar las siguientes ecuaciones mediante una
traslación de los ejes coordenados y trazarlas en ambos
sistemas coordenados:
i) x2  y 2  6x  4y  3  0
;
ii) y 2  2y  x  2  0
Solución.
i) x2  y 2  6x  4y  3  0
PABLO GARCÍA Y COLOMÉ
55
Se sustituyen las ecuaciones de traslación:
x  x ' h
 x ' h   y ' k 
2
2
y
y  y ' k
 6  x ' h  4  y ' k   3  0
x '2  2 x ' h  h2  y '2  2y ' k  k2  6x ' 6h  4y ' 4k  3  0
x '2  y '2   2h  6  x '  2k  4  y ' h2  k2  6h  4k  3  0
Se hacen cero los coeficientes de x ' y y ':
2h  6  0

h3
;
2k  4  0
; h2  k2  6h  4k  3  16
 x '2  y '2  16
Si ahora se sustituyen x ' y y ' por:
x'  x  3 y y'  y  2

k2
se obtiene una ecuación diferente de la original para la curva,
pero más sencilla de interpretar. Así,

 x  3   y  2
2
2
 16
La gráfica de esta curva, referida a ambos sistemas, se muestra
a continuación. Es una circunferencia con centro en el punto
3, 2 que son las coordenadas del nuevo origen O '.


Y
Y'
x
O '  3, 2 
O
X'
X
ii) y 2  2y  x  2  0
PABLO GARCÍA Y COLOMÉ
56
Se sustituyen las ecuaciones de traslación:
x  x ' h
y
y  y ' k
y 2  2y  x  2  0
 y ' k 
2
 2  y ' k    x ' h  2  0
y '2  2y ' k  k2  2y ' 2k  x ' h  2  0
y '2   2k  2  y ' x ' k2  2k  h  2  0
Se obtienen los valores de h y k :
2k  2  0  k  1 ; k2  2k  h  2  0  h  3
 y '2  x '  0  y '2   x '
Si se sustituyen x ' y y ' por: x '  x  3 y y '  y  1 se
obtiene una ecuación diferente de la original para la curva,
pero más sencilla de interpretar. Así,

 y  1
2
   x  3
La gráfica de esta curva, referida a ambos sistemas, se muestra
a continuación. Se trata de una parábola con vértice en el
punto 3,  1 que corresponde al vértice O ' :


Y
O
Y'
O '  3,  1
X
X'
PABLO GARCÍA Y COLOMÉ
57
ROTACIÓN DE LOS EJES COORDENADOS
DEFINICIÓN. Al cambio de posición de los ejes en el plano
coordenado, a partir de un giro en sentido antihorario,
conservando el mismo origen de coordenadas y los ejes con el
mismo sentido, se le conoce como rotación de ejes
coordenados.
En
estudio, se restringirá el giro de acuerdo a:
00    900 . Para determinar las ecuaciones de esta rotación
de los ejes coordenados, que expresan a las coordenadas de
un punto P x, y en términos de las nuevas coordenadas
x'
este
y


y ', producto de la rotación de los ejes, considérese la
siguiente figura:
De los triángulos rectángulos de la figura se obtiene:
x  d cos
Luego,
;
x'  a  d
x   x ' a cos
a  y 'tan

Y

d  x ' a
x  x 'cos   a cos 
x  x 'cos   y 'tan cos 
P  x, y  ; P  x ', y 
Y'
d


 y'
b
a
c
x
X'
X
 x  x 'cos  y ' sen
PABLO GARCÍA Y COLOMÉ
58
También de la figura,
y'
cos 
c
x '  a  d  a  y 'tan ; d 
sen
c
 x '  y 'tan 
sen
c
sen2
 x ' y 'tan  c  x ' sen  y '
sen
cos
2
y'
sen 
y
 x ' sen  y '
 y  x ' sen  y 'cos
cos
cos
y  bc
;
y '  b cos 

b
Por lo que las ecuaciones para la rotación son:
x  x 'cos  y ' sen
y  x ' sen  y 'cos 
Ejemplo. Obtener las nuevas coordenadas del punto
 4, 5
cuando los ejes coordenados experimentan una rotación de
600 .
Solución. Se sustituyen las coordenadas del punto considerado,
así como los valores de las funciones respectivas del ángulo
dado, en las ecuaciones anteriormente obtenidas y se llega a:
x  x 'cos   y ' sen

x ' 3y '  8
; 4
1
3
x '
y'
2
2
1
PABLO GARCÍA Y COLOMÉ
59
y  x ' sen  y 'cos 
Se despeja
3
1
x ' y '
2
2
2
; 5

3 x ' y '  10
x ' en 1 :
x '  3y ' 8

3

10  8 3

4
Se sustituye este valor en  2  y,
5
3 x '  2 3  10 
2
5
 x'  2 
3
2

y' 

3y ' 8  y '  10
y' 
5
2 3
2
3x ' 
15
2 3
2
Por lo tanto, las nuevas coordenadas del punto son:
5
5


2

3,

2
3


2
2


Ejemplo. Transformar la ecuación de la recta de ecuación
3 x  4y  12 mediante la rotación de sus ejes un ángulo de
450 . Trazar la gráfica de la recta con los dos sistemas de ejes
coordenados.
Solución. Se utilizan las ecuaciones de rotación y se obtiene:
x  x 'cos  y ' sen
;
x
2
2
x '
y'
2
2
PABLO GARCÍA Y COLOMÉ
60
y  x ' sen  y 'cos
;
y
2
2
x '
y'
2
2
Se sustituyen estas expresiones en la ecuación original de la
recta y,
3 x  4y  12
 2
 2
2 
2 
3
x '
y '  4 
x '
y '   12
 2



2
2


 2

3 2
3 2
4 2
4 2

x '
y '
x '
y '  12
2
2
2
2
7 2
2
2

x '
y '  12  7 x ' y '
 12
2
2
2
 7x ' y '  12 2
Y
 3 x  4y  12

7 x ' y '  12 2
Y'
X'
3
450
O' O
4
X
PABLO GARCÍA Y COLOMÉ
61
Ejemplo. Transformar la ecuación:
5x2  5y 2  8 x  6y  40  0
al rotar los ejes coordenados un ángulo
  ang tan
3
.
4
" "
tal que
Trazar la gráfica de la curva con los dos sistemas de ejes
coordenados.
Solución. Esta ecuación representa una circunferencia. Se
utilizan las ecuaciones de rotación obtenidas, sabiendo que si
los catetos de un triángulo rectángulo son 3 y 4 , entonces
la hipotenusa es 5 . Estos valores conforman un llamado
“triángulo mágico” que se muestra enseguida:
5

3
4
Entonces, con las ecuaciones de rotación, se obtiene:
x  x 'cos  y ' sen
;
y  x ' sen  y 'cos
;
4
3
x ' y '
5
5
3
4
y  x ' y '
5
5
x
Se sustituyen estas expresiones en la ecuación original de la
curva y,
5x2  5y 2  8 x  6y  40  0
2
2
3 
4 
3 
4 
4
3
4
3
5  x ' y '   5  x ' y '   8  x ' y '   6  x ' y '   40  0
5 
5 
5 
5 
5
5
5
5
9 2
16 2 
 16 2 24
 9 2 24
5
x' 
x ' y '
y '   5
x' 
x ' y '
y'  
25
25
25
25
 25

 25

PABLO GARCÍA Y COLOMÉ
62

32
24
18
24
x '
y ' x '
y ' 40  0
5
5
5
5
80 2 45 2 45 2 80 2 50
x' 
y' 
x' 
y' 
x ' 40  0
25
25
25
25
5
 x '2  y '2  2 x ' 8  0
que es la ecuación de la curva con respecto a los ejes rotados.
Otra forma de haber determinado la ecuación de la curva,
producto de la rotación, es mediante el álgebra y el
conocimiento de las cónicas. Se completan trinomios
cuadrados perfectos y,
5x2  5y 2  8 x  6y  40  0
8
16 16 
9
9 

 2 6
 5  x2  x 


5
y

y


 40  0



5
25 25 
5
25 25 


2
2
4
3  16 9


5 x    5 y   
  40  0
5
5
5 5


2
2
4 
3

 x    y    9
5 
5

4 3
Se trata de una circunferencia con centro en el punto  ,  y
5 5
radio r  3 . Y con las ecuaciones de rotación, es sencillo ver

que
se
llega
a
la
ecuación
de
la
circunferencia
 x ' 1  y '2  9, expresión que a partir del álgebra quedaría
2
2
2
como x '  y '  2 x ' 8  0 .
Ahora se presenta la gráfica de esta circunferencia cuya
representación al ser rotada es más sencilla que la original.
PABLO GARCÍA Y COLOMÉ
63
Y
Y'
X'
 4 3
C  , 
 5 5
 C ' 1, 0 

X
2
2

4 
3
 x     y    9
5 
5

2

2
 x ' 1  y '  9
Ejemplo. Dada la siguiente ecuación, mediante una rotación
convertirla en otra que no tenga término en " xy " , dar el
ángulo de giro y graficar la curva utilizando los conocimientos
sobre cónicas.
9x2  3 xy  9y 2  5  0
Solución. Se sustituyen las expresiones de la rotación de ejes
en la ecuación dada y se tiene que:
x  x 'cos  y ' sen
y  x ' sen  y 'cos
y
9  x 'cos   y ' sen   3  x 'cos   y ' sen  x ' sen  y 'cos   
2
9  x ' sen  y 'cos    5  0
2
9x '2 cos2   18 x ' y ' sen cos   9y '2 sen2  3 x '2 sen cos 
3 x ' y 'cos2   3 x ' y ' sen2  3y '2 sen cos   9x '2 sen2
18 x ' y ' sen cos   9y '2 cos2   5  0
9cos2   3 sen cos   9sen2 x '2  3cos2   3 sen2 x ' y '






 9sen2  3 sen cos   9cos2  y '2  5  0
PABLO GARCÍA Y COLOMÉ
64
Se iguala a cero el coeficiente del término en " xy " y en la
expresión obtenida se determina la nueva ecuación y el giro
correspondiente, utilizando identidades trigonométricas. Así,
3cos2   3 sen2  0

tan  1   

tan2   1

4
Se sustituye este valor con las funciones trigonométricas
correspondientes en la ecuación antes obtenida y se tiene
que:




2 
2  
2
2 
2  
9cos

3
sen
cos

9
sen
x
'

3cos

3
sen
x ' y '


4
4
4
4 
4
4 







  9sen2  3 sen cos  9cos2  y '2  5  0
4
4
4
4

  1
 1
 1  2   1 
 1
 1  2
9

3

9
x
'

9

3

9
 2
 2
2
 2 
2
 2  y '  5  0
 
 
 
 
  
  
21 2 15 2
x '  y '  5  0  21x '2  15y '2  10  0
2
2
Con operaciones algebraicas se identifica la cónica. Así,
x '2 y '2
x '2
y '2

1 

1
10 10
0.476 0.667
21 15
x '2
y '2


1
2
2
 0.69  0.817
x2 y 2
Que es una elipse con ecuación de la forma 2  2  1 , es
b
a
decir, con centro en el origen de coordenadas y semiejes:
PABLO GARCÍA Y COLOMÉ
65
0.69
en el eje de las abscisas y
ordenadas.
0.817
en el eje de las
Cabe aclarar que para los dos sistemas coordenados, XY y
X ' Y ' el origen es el mismo y sólo hay un giro de 450 del
segundo con respecto del primero.
Entonces la gráfica de esta elipse es la siguiente, donde es
claro que resulta mucho más fácil interpretarla y representarla
gráficamente cuando está rotada, dado el conocimiento que
se tiene de las cónicas y sus características analíticas y
geométricas. En la gráfica también se puede ver lo difícil que
sería, sin el auxilio de la computadora, el graficarla con la
ecuación que contiene el término en " xy " .
Y
Y'
1
X'
9x2  3 xy  9y 2  5  0

2
2
 21x '  15y '  10  0
1
1
X
1
PABLO GARCÍA Y COLOMÉ