La Transformada de Laplace
Definiciónde la transformada de Laplace
Propiedadesy transformadascomunes
Representaciónde sistemasLTI mediantela transformadade Laplace
Funciónde transferenciade sistemas de tiempocontinuo
La Transformadade Laplace
La Transformada de Laplace
Se ha visto que las herramientas del análisis de Fourier son en extremo útiles para el estudio de
muchos problemas de importancia práctica que involucran señales y sistemas LTI. Esto se debe en
gran parte al hecho de que una amplia clase de señales se puede representar mediante una
combinación lineal de exponenciales complejas, y éstas son funciones propias de los sistemas LTI. La
transformada continua de Fourier proporciona una representación para señales como combinaciones
lineales de exponenciales complejas de la forma 𝒆𝒔𝒕 con s = jω. Sin embargo, la propiedad de las
funciones propias presentada anteriormente, así como muchas de sus consecuencias, continúan
siendo aplicables a valores arbitrarios de s y no sólo a valores que son puramente imaginarios. Esta
observación conduce a una generalización de la transformada continua de Fourier, conocida como la
transformada de Laplace. Posteriormente, desarrollaremos la generalización correspondiente
discreta conocida como la transformada Z.
Las transformadas de Laplace y z poseen muchas de las propiedades que hacen del análisis de
Fourier una herramienta tan útil. Además, estas transformadas no sólo proporcionan herramientas y
conocimientos adicionales para las señales y sistemas que pueden analizarse con el uso de la
transformada de Fourier, sino que también pueden aplicarse en algunos contextos muy importantes
en los cuales no se puede usar las transformadas de Fourier. Por ejemplo, las transformadas de
Laplace y z se pueden aplicar al análisis de muchos sistemas inestables y en consecuencia juegan un
papel importante en la investigación de la estabilidad e inestabilidad de sistemas. Este hecho, junto
con las propiedades algebraicas que las transformadas de Laplace y z comparten con las
transformadas de Fourier, conduce a un conjunto muy importante de herramientas para el análisis de
sistemas y, en particular, para el análisis de los sistemas retroalimentados.
La Transformadade Laplace
Se vio anteriormente que la respuesta de un sistema lineal invariante en el tiempo (LTI) con
respuesta al impulso h(t) a una exponencial compleja con forma 𝒆𝒔𝒕 es
donde
Para una s imaginaria (es decir, s = jω), la integral en la ecuación (9.2) corresponde a la transformada
de Fourier de h(t). Con valores generales de la variable compleja s, a H(s), la transformada de
Laplace de la respuesta el impulso h(t), se le conoce como función de transferencia del sistema o,
simplemente, función del sistema.
La transformada de Laplace de una señal general x(t) se define como
y podemos observar que, en particular, es una función de la variable independiente s, la cual
corresponde a la variable compleja en el exponente de 𝒆−𝒔𝒕 . La variable compleja s puede escribirse
como s = σ + jω, siendo σ y ω las partes real e imaginaria, respectivamente.
La Transformadade Laplace
Para nuestra comodidad, algunas veces denotaremos la transformada de Laplace en forma de
operador como 𝓛{x(t)} y denotaremos la relación de transformación entre x(t) y X(S) como
Cuando s = jω, la ecuación (9.3) se convierte en
que corresponde a la transformada de Fourier de x(t); esto es,
La transformada de Laplace también conlleva una relación directa con la transformada de Fourier
cuando la variable compleja s no es puramente imaginaria. Para ver esta relación, considere una X(s)
tal como se especifica en la ecuación (9.3), con s expresada como s = σ + jω, de manera que
o
La Transformadade Laplace
Reconocemos el miembro derecho de la ecuación (9.8) como la transformada de Fourier de
𝒙(𝒕)𝒆−σ𝒕; es decir, la transformada de Laplace de x(t) puede interpretarse como la transformada de
Fourier de x(t) después de multiplicarla por una señal exponencial real. La exponencial real
𝒆−σ𝒕 puede ser creciente o decreciente en el tiempo, dependiendo de que σ sea positiva o negativa.
Para explicar la transformada de Laplace y su relación con la transformada de Fourier, consideremos
el siguiente ejemplo.
La Transformadade Laplace
En particular, observamos que, así como la transformada de Fourier no converge para todas las
señales, la transformada de Laplace puede converger para algunos valores de Re{s} pero no para
otros. En la ecuación (9.13), la transformada de Laplace converge sólo para σ = Re{s} > -a. Si a es
positiva, entonces X(s) se puede evaluar en σ = 0 para obtener
La Transformadade Laplace
Como se indica en la ecuación (9.6), para σ = 0 la transformada de Laplace es igual a la transformada
de Fourier, lo cual resulta evidente en el ejemplo anterior si comparamos las ecuaciones (9.9) y
(9.15). Si a es negativa o es cero, la transformada de Laplace aún existe pero no así la transformada
de Fourier.
La Transformadade Laplace
Comparando las ecuaciones (9.14) y (9.19), vemos que la expresión algebraica para la transformada
de Laplace es idéntica para las señales examinadas en los ejemplos 9.1 y 9.2. Sin embargo, de las
mismas ecuaciones vemos que el conjunto de valores de s para el cual la expresión es válida resulta
muy diferente en los dos ejemplos. Esto sirve para explicar el hecho de que, cuando se especifica la
transformada de Laplace de una señal, se requiere tanto la expresión algebraica como el intervalo
de valores de s para el cual esta expresión es válida. En general, el intervalo de valores de s para el
cual la integral en la ecuación (9.3) converge se conoce como la región de convergencia (que
abreviaremos como ROC, por sus siglas en inglés) de la transformada de Laplace. Es decir, la ROC
consiste en aquellos valores de s = σ + jω para los cuales la transformada de Fourier de 𝒙(𝒕)𝒆−σ𝒕
converge. Tendremos bastante más que decir acerca de la ROC conforme vayamos desarrollando
algunas ideas sobre las propiedades de la transformada de Laplace.
Una forma muy conveniente de representar la ROC se muestra en la figura 9.1 . La variable s es un
número complejo, y en la figura presentamos el plano complejo, que se conoce comúnmente como
el plano s asociado con esta variable compleja. Los ejes de las coordenadas son Re{s} en el eje
horizontal y Im{s} en el eje vertical. Los ejes horizontal y vertical algunas veces son llamados eje σ y
eje jω, respectivamente. La región sombreada en la figura 9.1(a) representa el conjunto de puntos en
el plano s que corresponden a la región de convergencia para el ejemplo 9.1. La región sombreada en
la figura 9.1(b) indica la región de convergencia del ejemplo 9.2.
La Transformadade Laplace
La Transformadade Laplace
La Transformadade Laplace
La Transformadade Laplace
En cada uno de los cuatro ejemplos anteriores, la transformada de Laplace es racional, es decir, una
relación de polinomios de la variable compleja s tal que
donde N(s) y D(s) son el polinomio del numerador y el polinomio del denominador, respectivamente.
Como sugieren los ejemplos 9.3 y 9.4, X(S) será racional siempre que x(t) sea una combinación lineal
de exponenciales reales o complejas. Como se verá más adelante, las transformadas racionales
también surgen cuando examinamos los sistemas LTI especificados en términos de ecuaciones
diferenciales lineales con coeficientes constantes. Excepto por un factor escala, los polinomios del
numerador y del denominador en una transformada racional de Laplace pueden especificarse por sus
raíces; por lo tanto, marcar la localización de las raíces de N(s) y D(s) en el plano s indicando la ROC
proporciona una forma gráfica conveniente para describir la transformada de Laplace. Por ejemplo,
en la figura 9.2(a) mostramos la representación en el plano s de la transformada de Laplace del
ejemplo 9.3, señalando con una “Χ” la localización de cada raíz del polinomio del denominador de la
ecuación (9.23) y con una “O” la localización de la raíz del polinomio del numerador en la ecuación
(9.23). La gráfica que corresponde a las raíces de los polinomios del numerador y denominador para
la transformada de Laplace en el ejemplo 9.4 se encuentra en la figura 9.2(b). La region de
convergencia para cada uno de estos ejemplos se ha indicado con un área sombreada en la gráfica
correspondiente.
La Transformadade Laplace
La Transformadade Laplace
Para las transformadas racionales de Laplace, las raíces del polinomio del numerador son
comúnmente conocidas como ceros de X(s), ya que para esos valores de s, X(s) = 0. Las raíces del
polinomio del denominador son conocidas como los polos de X(s), y para esos valores de s, X(s)
tiende a ser infinita, es decir, X(s) → ∞. Los polos y ceros de en el plano s finito caracterizan por
completo la expresión algebraica para X(s) dentro de un factor de escala. La representación de X(s)
mediante sus polos y ceros en el plano s se conoce como el diagrama de polos y ceros de X(s). Sin
embargo, como vimos en los ejemplos 9.1 y 9.2, el conocimiento de la forma algebraica de X(s) por
sí solo no identifica la ROC para la transformada de Laplace. Es decir, una especificación completa
que llegue hasta dentro de un factor escala de una transformada racional de Laplace consiste de un
diagrama de polos y ceros de la transformada junto con su ROC (la cual, por lo general, se muestra
como una región sombreada en el plano s, como en las figuras 9.1 y 9.2).
Asimismo, si bien los polos y ceros no son necesarios para especificar la forma algebraica de una
transformada racional X(s), algunas veces resulta conveniente referirse a ellos en el infinito. En
concreto, si el orden del polinomio del denominador es mayor que el orden del polinomio del
numerador, entonces X(s) tiende a cero conforme s se aproxime a infinito. Por lo contrario, si el
orden del polinomio del numerador es mayor que el orden del polinomio del denominador, entonces
X(s) será ilimitada conforme s se aproxime a infinito. Este comportamiento se puede interpretar
como los ceros o polos en el infinito. Por ejemplo, la transformada de Laplace de la ecuación (9.23)
tiene un denominador de orden 2 y un numerador de sólo orden 1, así que en este caso X(s) tiene un
cero en el infinito. Lo mismo es válido para la transformada de la ecuación (9.30), en la cual el
numerador es de orden 2 y el denominador es de orden 3. En general, si el orden del denominador
excede el orden del numerador por k, X(s) tendrá k ceros en el infinito. De manera similar, si el orden
del numerador excede el orden del denominador por k, X(s) tendrá k polos en el infinito.
La Transformadade Laplace
La Transformadade Laplace
Recordemos, de la ecuación (9.6), que
para s = jω la trasformada de Laplace
corresponde a la transformada de
Fourier. Sin embargo, si la ROC de la
transformada de Laplace no incluye el
eje jω (es decir, Re{s} = 0), entonces la
transformada de Fourier no converge.
Como se ve en la figura 9.3, de hecho
éste es el caso en el ejemplo 9.5, el
cual es consistente con el hecho de
que el término (1/3)𝒆𝟐𝒕 𝒖(𝒕) en x(t) no
tiene transformada de Fourier.
Observe también en este ejemplo que los dos ceros en la ecuación (9.35) ocurren en el mismo valor
que s. En general, nos referiremos al orden de un polo o de un cero como el número de veces que se
repite en una ubicación dada.
En el ejemplo 9.5 hay un cero de segundo orden en s = 1 y dos polos de primer orden, uno en s = -1 y
el otro en s = 2. En este ejemplo, la ROC queda a la derecho del polo situado más hacia la derecho. En
general, para las transformadas racionales de Laplace hay una estrecha relación entre las
localizaciones de los polos y las posibles ROC que pueden ser asociadas con un diagram dado de
polos y ceros. Las restricciones específicas en la ROC están estrechamente ligadas a las propiedades
de x(t) en el dominio del tiempo.
La Transformadade Laplace
Región de Convergencia para las Transformadas de Laplace
Como se vio anteriormente, una especificación completa de la transformada de Laplace requiere no
sólo de la expresión algebraica de X(s), sino también de la región de convergencia asociada. Como se
evidenció en los ejemplos 9.1 y 9.2, dos señales muy diferentes pueden tener idénticas expresiones
algebraicas para X(s), de manera que sus transformadas de Laplace se podrían distinguir únicamente
por la región de convergencia. Ahora exploraremos algunas restricciones específicas de la ROC para
varias clases de señales. La comprensión de estas restricciones a menudo nos permite especificar de
manera implícita o reconstruir la ROC únicamente a partir del conocimiento de la expresión
algebraica X(s) y de ciertas características generales de x(t) en el dominio del tiempo. A continuación
se presentan las propiedades de la ROC y se deja al estudiante el análisis de las comprobaciones de
las mismas, presentadas en el libro de texto.
La validez de esta propiedad radica en el hecho de que la ROC de X(s) consiste de aquellos valores de
s = σ + jω para los cuales la transformada de Fourier de 𝒙(𝒕)𝒆−σ𝒕 converge. Esto es, la ROC de la
transformada de Laplace de x(t) consiste de aquellos valores de s para los cuales 𝒙(𝒕)𝒆−σ𝒕 es
absolutamente integrable.
Y ello se deriva de la propiedad 1, ya que esta condición depende sólo de σ, la parte real de s.
La Transformadade Laplace
Esta propiedad se observa fácilmente en todos los ejemplos estudiados hasta ahora. Puesto que X(s)
es infinita en un polo, la integral en la ecuación (9.3) claramente no converge a un polo y, por lo
tanto, la ROC no puede contener valores de s en esos polos.
La intuición de este resultado se sugiere en las figuras 9.4 y 9.5. Específicamente, una señal de
duración finita tiene la propiedad de ser cero fuera de un intervalo de duración finita, tal como
se ilustra en la figura 9.4
La Transformadade Laplace
En la figura 9.5(a) mostramos la x(t) de la figura 9.4 multiplicada por una exponencial
decreciente y en la 9.5(b) la misma señal multiplicada por una exponencial creciente. Puesto
que el intervalo sobre el cual x(t) es diferente de cero es finito, la exponencial ponderada
nunca es ilimitada, y en consecuencia, resulta razonable que la integrabilidad de x(t) no se
altere por esta ponderación exponencial (ver comprobación).
Es importante reconocer que, para asegurarse de que la ponderación exponencial esté
limitada sobre un intervalo en el cual x(t) sea diferente de cero, el análisis anterior depende en
gran medida del hecho de que x(t) es de duración finita.
La Transformadade Laplace
La Transformadade Laplace
Una señal del lado derecho o simplemente derecha es aquella para la cual x(t) = 0 antes de algún
tiempo 𝑻𝟏 , como se ilustra en la figura 9.6. Es posible que para tal señal no haya un valor de s en el
𝟐
que la transformada de Laplace converja. Un ejemplo es la señal 𝒙 𝒕 = 𝒆𝒕 𝒖(𝒕). Sin embargo, si
existe convergencia para un valor de s con parte real σ𝟎 , entonces habrá convergencia para todos loa
valores de s a su derecha (es decir, para los cuales Re{s} > σ𝟎 , ver comprobación). Por esta razón, la
ROC en el presente caso se conoce comúnmente como semiplano derecho.
La Transformadade Laplace
Una señal del lado izquierdo o simplemente izquierda es aquella para la cual x(t) = 0 después de
algún tiempo 𝑻𝟐 , como se ilustra en la figura 9.8. Asimismo, para una señal izquierda, la ROC se
conoce por lo general como semiplano izquierdo, ya que si un punto s esta en la ROC, todos los
puntos a la izquierda de s estarán en la ROC.
Una señal bilateral es aquella que tiene extensión infinita tanto para t > 0 como para t < 0, tal como
se ilustra en la figura 9.9(a). Para tales señales, la ROC puede examinarse escogiendo un tiempo
arbitrario 𝑻𝟎 y dividiendo x(t) en In suma de una señal derecha 𝒙𝑹 (𝒕) y una señal izquierda 𝒙𝑳 (𝒕)
como se indica en las figuras 9.9(b) y (e).
La Transformadade Laplace
La transformada de Laplace de x(t) converge para valores de s en los cuales las transformadas de
ambas señales (𝒙𝑹 (𝒕) y 𝒙𝑳 (𝒕)) convergen. De acuerdo con la propiedad 4, la ROC de 𝓛{𝒙𝑹 (𝒕)}
consiste en un semiplano definido por Re{s} > σ𝑹 para algún valor de σ𝑹 , de acuerdo con la
propiedad 5 la ROC de 𝓛{𝒙𝑳 (𝒕)} consiste en un semiplano definido por Re{s} < σ𝑳 para algún valor de
σ𝑳 . La ROC de 𝓛{𝒙(𝒕)} es entonces la superposición de estos dos semiplanos, como se indica en la
figura 9.10. Con lo anterior se da por hecho que σ𝑹 < σ𝑳 , de manera que hay algo de traslape. Si éste
no es el caso, entonces no existirá la transformada de Laplace de x(t), aun cuando las transformadas
de Laplace de 𝒙𝑹 (𝒕) y 𝒙𝑳 (𝒕) existan en forma individual.
La Transformadade Laplace
La Transformadade Laplace
La Transformadade Laplace
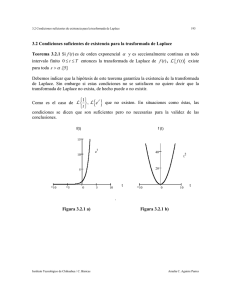
Observe que cualquier señal, o no tiene transformada de Laplace o cae en una de las cuatro
categorías cubiertas por las propiedades 3, 4, 5 y 6. Por lo tanto, para cualquier señal que tenga
transformada de Laplace, la ROC debe ser el plano s completo (para señales de longitud finita), o el
semiplano izquierdo (para señales del lado izquierdo), o el semiplano derecho (para señales del
lado derecho), o una sola franja (para señales bilaterales). En todos los ejemplos que hemos
considerado, la ROC tiene la propiedad adicional de que en cada dirección (es decir, Re{s} se
incrementa y Re{s} disminuye) está limitada por polos o se extiende al infinito. De hecho, esto
siempre es cierto para transformadas racionales de Laplace.
La Transformadade Laplace
Una argumentación formal para esta propiedad resulta un tanto tediosa, pero su validez es
esencialmente una consecuencia del hecho de que una señal con una transformada racional de
Laplace consiste de una combinación lineal de exponenciales y, a partir de los ejemplos 9.1 y 9.2, del
hecho de que la ROC de la transformada de los términos individuales en esta combinación lineal
debe tener esta propiedad. Como consecuencia de la propiedad 7, junto con las propiedades 4 y 5,
tenemos la
La Transformadade Laplace
La Transformadade Laplace
La Transformada Inversa de Laplace
Analizamos anteriormente la interpretación de la transformada de Laplace de una señal como la
transformada de Fourier de una versión exponencialmente ponderada de la señal; esto es, cuando s
se expresa como s = σ + jω, la transformada de Laplace de una señal x(t) está dada por
para valores de s = σ + jω en la ROC. Podemos invertir esta relación usando la transformada inversa
de Fourier . Esto es,
o, multiplicando ambos lados por 𝒆σ𝒕 , obtenemos
Esto es, podemos recuperar x(t) a partir de una transformada de Laplace evaluada para un conjunto
de valores de s = σ + jω en la ROC, teniendo una σ fija y con una ω que varía de -∞ a +∞. Podemos
remarcar esto y obtener algún aprendizaje adicional sobre la forma de recuperar x(t) a partir de X(s)
si cambiamos la variable de integración en la ecuación (9.55), de ω a s, y nos valemos del hecho de
que σ es constante, de modo que ds = j dω.
La Transformadade Laplace
El resultado es la ecuación básica de la transformada inversa de Laplace:
Esta ecuación indica que x(t) puede representarse como una integral ponderada de exponenciales
complejas. El contorno de la integración en la ecuación (9.56) es la línea recta en el plano s,
correspondiente a todos los puntos s que satisfacen Re{s} = σ. Esta Iínea es paralela al eje jω.
Además, podemos seleccionar cualquier línea en la ROC, es decir, podemos seleccionar cualquier
valor de σ tal que X(σ + jω) converja. La evaluación formal de la integral para una X(s) general
requiere del uso de la integración de contornos en el plano complejo, un tema que no
consideraremos aquí. Sin embargo, para la clase de transformadas racionales. la transformada
inversa de Laplace se puede determinar sin la evaluación directa de la ecuación (9.56), utilizando la
técnica de expansión por fracciones parciales de una manera similar a la que se usó para determinar
la transformada inversa de Fourier. Básicamente, el procedimiento consiste en expandir la expresión
algebraica racional en una combinación de términos de menor orden.
Por ejemplo, suponiendo que no hay polos de orden múltiple y que el orden del polinomio de
denominador es mayor que el orden del polinomio del numerador, X(s) se puede expandir en la
siguiente forma:
Ver anexo sobre fracciones parciales
La Transformadade Laplace
A partir de la ROC de X(s) se puede inferir la ROC de cada uno de los términos individuales en la
ecuación (9.57) y entonces, a partir de los ejemplos 9.1 y 9.2 se puede determinar la transformada
inversa de Laplace de los términos individuales. Hay dos posibles selecciones para la transformada
inversa de cada término 𝑨𝒊 /(𝒔 + 𝒂𝒊 ) en la ecuación. Si la ROC se encuentra a la derecha del polo en
𝒔 = −𝒂𝒊 , entonces la transformada inversa de este término es 𝑨𝒊 𝒆−𝒂𝒊 𝒕 𝒖(𝒕), una señal derecha . Si
la ROC está a la izquierda del polo en 𝒔 = −𝒂𝒊 , entonces la transformada inversa de este términos
es −𝑨𝒊 𝒆−𝒂𝒊 𝒕 𝒖(−𝒕), una señal izquierda. Sumando las transformadas inversas de los términos
individuales en la ecuación (9.57) se obtiene la transformada inversa de X(s). Es más conveniente
presentar los detalles del procedimiento mediante varios ejemplos.
Ver anexo sobre fracciones parciales
La Transformadade Laplace
Ver anexo sobre fracciones parciales
La Transformadade Laplace
La Transformadade Laplace
Ver anexo sobre fracciones parciales
La Transformadade Laplace
Propiedades de la Transformada de Laplace y Pares de Transformadas de Laplace
La table 9.1 resume las propiedades de la transformada de Laplace. Se recomienda al estudiante
consultar las comprobaciones matemáticas de estas propiedades en el libro de texto. Muchas de
estas propiedades son utilizadas para el análisis y caracterización de sistemas LTI.
La Transformadade Laplace
La transformada inversa de Laplace a menudo se puede evaluar mediante la descomposición de X(s)
en una combinación lineal de términos más sencillos, de los cuales puede reconocerse con facilidad
la transformada inversa de cada uno de ellos. La tabla 9.2 enumera varios pares útiles de la
Transformada de Laplace.
El primer par de transformadas se
deduce directamente de la ecuación
(9.3). Los pares de transformadas 2 y 6 se
obtienen de manera directa a partir del
ejemplo 9.1 con a = 0 y a = α,
respectivamente. El par de
transformadas 4 se desarrolló en el
ejemplo 9.14 mediante la propiedad de
diferenciación. El par de transformada 8
se deduce a partir del par 4 usando la
propiedad definida en la sección 9.5.3.
Los pares de transformada 3, 5, 7 y 9 se
basan en los pares 2, 4, 6 y 8,
respectivamente, hunto con la propiedad
de escalamiento en tiempo de la sección
9.5.4 con a = -1. De manera similar, los
pares de transformadas 10 a 16 pueden
obtenerse a partir de los pares anteriores
de la table usando las propiedades
adecuadas de la table 9.1.
La Transformadade Laplace
La Transformadade Laplace
Como se demuestra en el siguiente ejemplo, este par específico de transformadas de Laplace es un
particular útil cuando se aplica a la expansión en fracciones parciales para determinar la
transformada inversa de Laplace de una función con polos de orden múltiple
La Transformadade Laplace
Ver anexo sobre fracciones parciales
La Transformadade Laplace
Análisis y Caracterización de Sistemas LTI usando la Transformada de Laplace
Una de las aplicaciones mas importantes de la transformada de Laplace es el análisis y
caracterizaci6n de los sistemas LTI. Su papel para esta clase de sistemas proviene directamente de Ia
propiedad de convolución. En concreto, las transformadas de Laplace de la entrada y de la salida de
un sistema LTI están relacionadas a través de la multiplicación por la transformada de Laplace de la
respuesta al impulso del sistema. Por lo tanto,
donde X(s), Y(s) y H(s) son las transformadas de Laplace de la entrada, de la salida y de la respuesta
al impulso del sistema, respectivamente. La ecuación (9.112) es la contraparte, en el contexto de las
transformadas de Laplace, de la ecuación (4.56) que se desarrolló para la transformada de Fourier.
De hecho, para s = jω, cada una de las transformadas de Laplace en la ecuación (9.112) se reduce a
Ias transformadas de Fourier respectivas y la ecuación corresponde exactamente a la (4.56).
Asimismo, a partir de nuestro análisis en clases anteriores sobre la respuesta de los sistemas LTI a
exponenciales complejas, si la entrada de un sistema LTI es 𝒙 𝒕 = 𝒆𝒔𝒕 , entonces la salida será
𝑯(𝒔)𝒆𝒔𝒕, es decir, 𝒆𝒔𝒕 es una función propia del sistema con valor propio igual a la transformada de
Laplace de la respuesta al impulso.
La Transformadade Laplace
Para s= jω, H(s) es la respuesta en frecuencia del sistema LTI. En el contexto más amplio de la
transformada de Laplace, H(s) se conoce comúnmente como la función de transferencia del sistema
o, de forma alterna, como la función del sistema. Muchas propiedades de los sistemas LTI pueden
estar estrechamente asociadas con las características de la función de transferencia del sistema en
el plano s. Se deja al estudiante al análisis de las comprobaciones de estas propiedades
proporcionadas en el libro de texto, para fin de la clase en aula, nos limitamos a enunciar estas
características a continuación.
• Causalidad
La Transformadade Laplace
La Transformadade Laplace
De una manera exactamente análoga, podemos definir el concepto de anticausalidad. Un sistema es
anticausal si su respuesta al impulso h(t) = 0 para t > 0. Debido a que en ese caso h(t) estaría del lado
izquierdo, sabemos que la ROC de la función del sistema H(s) debe estar en un semiplano izquierdo.
Una vez más, en general lo recíproco no se cumple. Es decir, si la ROC de H(s) es un semiplano
izquierdo, lo único que sabemos es que h(t) es izquierda. Sin embargo, si H(s) es racional, entonces el
tener una ROC a la izquierda del polo ubicado mas hacia la izquierda equivale a que el Sistema sea
anticausal.
• Estabilidad
La Transformadade Laplace
La Transformadade Laplace
Sistemas LTI caracterizados por ecuaciones diferenciales lineales con coeficientes
constante
En clases anteriores analizamos el uso de la transformada de Fourier para obtener la respuesta en
frecuencia de un sistema LTI caracterizado por una ecuación diferencial lineal con coeficientes
constantes sin obtener primero la respuesta al impulso o la solución en el dominio del tiempo. De
una manera exactamente análoga, las propiedades de la transformada de Laplace pueden utilizarse
para obtener directamente la función del sistema para un sistema LTI caracterizado por una ecuación
diferencial lineal con coeficientes constantes. Ilustramos este procedimiento en el siguiente ejemplo.
La Transformadade Laplace
El mismo procedimiento usado para obtener H(s) a partir de la ecuación diferencial en este ejemplo
puede ser aplicado en forma mas general. Considere una ecuación diferencial lineal con coeficientes
constantes de la forma
La Transformadade Laplace
Aplicando la transformada de Laplace en ambos miembros y usando las propiedades de linealidad y
diferenciación repetidamente, obtenemos
o
Por tanto, la función de transferencia del sistema para un sistema especificado por una ecuación
diferencial siempre es racional, con ceros en las soluciones de
y polos en las soluciones de
La Transformadade Laplace
De manera congruente con nuestro análisis previo, la ecuacion (9.133) no incluye una especificación
de la región de convergencia de H(s), ya que la ecuacion diferencial lineal con coeficientes constantes
por sí misma no define o limita la región de convergencia. Sin embargo, esta región se puede inferir si
se cuenta con información adicional, tal como la estabilidad o causalidad del sistema. Por ejemplo, si
imponemos la condición de reposo inicial en el sistema, de manera que sea causal, la ROC estará a la
derecha del polo ubicado más hacia la derecha.
La Transformadade Laplace
Como hemos visto hasta ahora, las propiedades de los sistemas como la causalidad y la estabilidad se
pueden relacionar de manera directa con la función del sistema y sus características. De hecho, cada
una de las propiedades de las transformadas de Laplace que hemos descrito se pueden usar de esta
manera para relacionar el comportamiento del sistema con la función del sistema. A continuación
daremos varios ejemplos que explican lo anterior.
La Transformadade Laplace
La Transformadade Laplace
La Transformadade Laplace