APUNTES DOCENTES
ASIGNATURA: CÁLCULO DIFERENCIAL
PROFESOR: ING. EDGAR VARGAS RUIZ
I - 2012
UNIDADES TECNOLÓGICAS DE SANTANDER
UNIDAD 1
DESIGUALDADES Y FUNCIONES
DESIGUALDADES
En estudios anteriores habremos visto las igualdades; tema relacionado con la solución de
ecuaciones lineales y cuadráticas. El estudio de las DESIGUALDADES es útil, cuando el valor
aproximado de una cantidad, interesa más que su valor exacto.
La palabra desigualdad sirve para decir que una cantidad es mayor o menor que otra, para ello
utilizamos los símbolos:
: Mayor o igual que.
: Menor o igual que.
>: Mayor que.
<: Menor que.
Una desigualdad numérica es una comparación entre dos números a y b, utilizando los símbolos de
desigualdad: “>”, “mayor que”; “<” menor que”; “ ”, “mayor o igual que”; “ ”, “menor o igual que”.
PROPIEDADES DE LAS DESIGUALDADES
Si a, b y c son tres números reales, se cumple que:
1.
Si a > b
y
b > c, entonces
a > c (Transitiva)
Si a < b
y
b < c, entonces
a<c
(a c) > (b c)
(a c) < (b c).
2.
Si a > b, entonces
Si a < b, entonces
3.
Si a > b
Si a > b
4.
Si a > b y c > 0,
entonces
Si a > b y c < 0,
entonces
y
y
c > 0, entonces
c < 0, entonces
ac > bc
ac < bc.
a b
c c
a b
c c
5. Si a > b
y
c > d, entonces
a+c > b+d (Aditiva)
6. Si a > b
y
c > d, entonces
ac > bd
7. Si a > b
y
a > 0 y b>0, entonces
8. Si a > b,
entonces
an > bn
1 1
a b
Página
2
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
a 0 b 0
9. a b 0, si
a 0 b 0
a 0 b 0
a b 0, si
a 0 b 0
10. Al intercambiar los miembros de una desigualdad, se modifica el sentido de la misma.
36 6 3
Las desigualdades se dividen en dos clases: absolutas y condicionales
Ejemplo
a. Desigualdades absolutas: o incondicionales, son semejantes a las identidades.
Son satisfechas por todos los números Reales
Ejemplo:
2ab
ab
ab
Su validez se establece por medio de una demostración analítica (utilizando propiedades de las
desigualdades).
b. Desigualdades condicionales: son llamadas Inecuaciones, sólo son satisfechas por algunos
números Reales. Son desigualdades que poseen términos desconocidos
Ejemplo:
2x 6 0
INTERVALOS
Los intervalos son subconjuntos de los números reales, determinados por las desigualdades, que
se representan geométricamente mediante segmentos de recta o semirrectas. Por lo tanto, las
operaciones entre conjuntos también se aplican a los intervalos. Veremos a continuación las
diferentes clases de intervalos que existen y luego algunos ejemplos.
CLASES DE INTERVALOS
Página
3
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Ejemplo
Sean los intervalos A = [–5, 5], B = (– , 8]
1. A C
2. B C
3.
y C = (2, ); hallar en las diferentes notaciones:
AC B
Solución:
1.
2.
3.
A C = [–5, ] Notación intervalo
AC =
x / x 5 Notación de conjunto
x / 2 x 8 Notación de conjunto
B C =
2, 8 Notación intervalo
A C B = 2, 5 , 8 = , 8 Notación intervalo
A C B = x / x 8 Notación de conjunto
B C =
INECUACIONES
Una inecuación es una desigualdad en la que hay una o más cantidades desconocidas
(incógnitas) y que sólo se verifica (o demuestra) para determinados valores de las incógnitas. Las
inecuaciones también se conocen como desigualdades condiciónales, como se mencionó
anteriormente.
La desigualdad 2x - 3 > x + 5 es una inecuación porque tiene la incógnita x y
sólo se verifica para cualquier valor de x mayor que 8. Para x = 8 se convertiría
en una igualdad y para x < 8 en una desigualdad de signo contrario.
Para resolver una inecuación deben encontrarse los valores de las incógnitas que satisfagan la
inecuación.
Página
4
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
La resolución de inecuaciones se fundamenta en las propiedades de las desigualdades
anteriormente enunciadas y en las consecuencias que de las mismas se derivan. (La solución a
una inecuación se da mediante un intervalo).
Solución de inecuaciones
Resolver una inecuación consiste en aplicar las propiedades de las desigualdades antes expuestas
para hallar un conjunto de valores que hace posible la desigualdad. La solución de una inecuación
recibe el nombre de conjunto solución. Y puede expresarse de tres formas diferentes: en notación
de intervalo, en notación de conjunto y en forma gráfica. (Ver tabla de “clases de intervalos”)
CLASIFICACIÓN DE LAS INECUACIONES
Las inecuaciones se clasifican atendiendo al número de incógnitas y al grado de la expresión
algebraica que aparece en ellas.
Ejemplo:
INECUACIÓN
TIPO
2x-3 > x-5
x-3 ≥ y
x2-5x ≤ 4
xy-3 > 0
1º grado; 1 incógnita
1º grado; 2 incógnita
2º grado; 1 incógnita
2º grado; 2 incógnita
INECUACIONES DE UNA VARIABLE
1. INECUACIONES LINEALES O DE PRIMER GRADO
Las inecuaciones de 1er grado con una incógnita son las que responden a las siguientes formas
básicas:
ax + b < 0
ax + b > 0
ax + b ≤ 0
ax + b ≥ 0
En la mayoría de los casos conviene seguir el siguiente procedimiento:
1.
2.
3.
4.
5.
6.
7.
Quitar los paréntesis, si los hay.
Quitar denominadores, si los hay. Para ello, se multiplica los dos miembros de la ecuación
por el m.c.m. de los denominadores.
Pasar los términos en x a un miembro (normalmente al primero) y los números al otro.
Reducir términos semejantes, con lo que se llega a una ecuación de forma básica.
Si el coeficiente de la x es negativo multiplicamos por −1, por lo que cambiará el
sentido de la desigualdad.
Despejar la x (la incógnita).
Obtener la solución en forma de desigualdad, en forma de intervalo o grafica.
x 2 5( x 7) 7 x
3
4
2
4( x 2) 3(5 x 35) 6(7 x)
12
12
Ejemplo 1: Resolver
4 x 8 15x 105 42 6 x
5x 55
Página
5
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
5x 55 x 11
S= x (-, 11)
2x 3 x 5
Ejemplo 2: Resolver
Pasando x al primer miembro y 3 al segundo se tiene:
2x x 3 5
x 8
S 8, x R / x 8
Reduciendo términos:
(
8
x
5x
Ejemplo 3: Dada la siguiente inecuación 7 2 3 6 . Halle el conjunto solución y
grafíquelo.
Suprimiendo denominadores (m.c.m. = 6) se tiene: 42 3x 10x 36
3x 10x 36 36
Trasponiendo términos:
13x 78
Cambiando el signo a los dos miembros, lo cual hace cambiar el signo de la desigualdad original:
13x 78
Dividiendo por 13: x <
78
o sea, x < 6
13
S ,6 x R / x<6
)
6
Ejemplo 4: Resolver
x 3 x 1 x 1
2
3x
Efectuando las operaciones indicadas:
x 2 2 x 3 x 2 2 x 1 3x
Suprimiendo x 2 en ambos miembros y transponiendo:
2 x 2 x 3x 1 3
Página
6
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
S , 4
x4
x R / x<4
)
4
Ejemplo 5: Dada la siguiente inecuación
x 2 2x 2 1 1
x 2 . Halle el conjunto solución y
3
2
4
grafíquelo.
Se encuentra el m.c.m. (2, 3, 4) = 12 y se multiplica por 12 ambos miembros de la inecuación para
obtener:
4 x 2 6 2 x 2 1 3 12 x 2
4 x 8 12 x2 6 3 12 x2
Pasando todas las variables al lado izquierdo de la inecuación, se obtiene:
4x 6 3 8
Despejando la variable x de la inecuación, se obtiene:
x
5
4
5
5
S , x R / x
4
4
5/4
Solución de inecuaciones simultáneas de primer grado
Una inecuación simultánea es una inecuación con desigualdad doble; Si a < x < b entonces x >a
x < b, es decir, el conjunto solución es la intersección de los dos conjuntos solución:
S x / x a x / x b
Ejemplo: Hallar el conjunto solución de
6 4x 2 7
Separando en dos desigualdades:
4x 2 6
4x 2 7
4x 6 2
4x 7 2
x
8
4
x2
9
4
9
x
4
x
Sol: x 2,
9
4
2. INECUACIONES CUADRÁTICAS O DE SEGUNDO GRADO
Página
7
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Las inecuaciones de 2º grado con una incógnita son las que se presentan según alguna de las
siguientes formas básicas:
ax2+bx+c < 0
ax2+bx+c > 0
ax2+bx+c ≤ 0
ax2+bx+c ≥ 0
Procedimiento
Primer Paso: Igualamos el polinomio del primer miembro a cero y obtenemos las raíces de la
ecuación de segundo grado factorizando el polinomio o usando la formula cuadrática.
Segundo Paso: Considerar los casos necesarios para que se cumpla la inecuación.
Tercer Paso: Realice la intersección o unión de los conjuntos solución de acuerdo al caso
seleccionado.
Cuarto Paso: dar la solución en forma de intervalos y graficarla.
Ejemplo
Dada la siguiente inecuación x2 5x 6 0 . Halle el conjunto solución y grafíquelo.
Primer paso: Factorizar el polinomio dado x 2 5x 6 x 3 x 2 , quedando una inecuación de
la forma:
x 3 x 2 0
Segundo paso: Los casos que se deben considerar son los siguientes:
Caso I: Cuando ambos binomios son positivos es decir:
x 3 0
y
x 2 0
Caso II: Cuando ambos binomios son negativos, es decir:
x 3 0
y
x 2 0
Solución Caso I:
Sea SA el conjunto solución de la inecuación x 3 0 y SB al conjunto solución de la inecuación
x 2 0 , la solución del Caso I viene dada por: SI SA SB
Solución para SA
x3 0
x 3
S A 3, x R / x 3
Solución para SB
x20
x 2
SB 2, x R / x 2
La solución para SI es entonces:
Página
8
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
SI SA SB 3, 2, 2,
SI 2, x R / x 2
(
(
–3
–2
Solución Caso II:
Si llamamos SC al conjunto solución de la inecuación
x 3 0
y SD al conjunto solución de la
inecuación x 2 0 , la solución del Caso II viene dada por: SII SC SD
Solución para SC :
x 3 0
x 3
Sc , 3 x R / x 3
Solución para SD :
x20
x 2
Sd , 2 x R / x 2
La solución para SII es entonces:
SII Sc Sd , 3 , 2 , 3
SII , 3 x R / x 3
)
-3
)
-2
Solución General
La solución general será la unión de SI y SII , es decir:
SG SI SII 2, , 3
El método que acaba de estudiarse, para resolver inecuaciones cuadráticas se llama método
analítico. Existe un método alternativo, el método gráfico, que también se conoce como el
método del Cementerio o método de las cruces. El procedimiento para resolver inecuaciones
cuadráticas utilizando este método consiste igualmente en Factorizar el polinomio cuadrático,
encontrar las raíces reales y ubicarlas sobre la recta real, dando origen de esta manera a intervalos
en la recta. Luego, para cada intervalo, se va evaluando cada binomio para determinar el signo de
éste, es decir, se le asignará a la variable, un valor arbitrario que pertenezca a cada intervalo para
conseguir el signo de cada binomio. Por último, se seleccionan los intervalos para los cuales se
cumple la desigualdad.
Ejemplo 1
Página
9
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Dada la siguiente inecuación x2 5x 6 0 , halle el conjunto solución y grafique.
Se factoriza el polinomio x 2 5x 6 x 3 x 2 , quedando la inecuación de la forma:
x 3 x 2 0
Las raíces que anulan
x 3 x 2
son x 3 y x 2 . (Valores críticos) Se ubican sobre la
recta real (ver cuadro 1). Se le asignan valores arbitrarios a x en cada intervalo, y se determinan
los signos.
Cuadro 1. Raíces ubicadas en la recta real.
Se aprecia en el cuadro anterior que la desigualdad se cumple para aquellos intervalos donde el
producto de los dos binomios es positivo por ser la inecuación > 0, por lo tanto la solución viene
dada por:
SG , 3 2,
Ejemplo 2
Dada la siguiente inecuación
x 1
2
2
x 1
3
2
8
, halle el conjunto solución y grafique.
3
Se desarrollan los productos notables, se multiplican por 6 ambos miembros de la inecuación y se
reducen términos semejantes, obteniendo:
x2 2 x 15 0
Factorizando
el polinomio resultante, se tiene
inecuación de la forma:
Las raíces de
x2 2 x 15 x 5 x 3 , resultando una
x 5 x 3 0
x 5 x 3
son x 5 y x 3 (valores críticos), las cuales se ubican sobre la
recta real. Se le asignan valores arbitrarios a x en cada intervalo, y se determinan los signos de la
desigualdad.
Página
10
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Se aprecia en el cuadro anterior que la desigualdad se cumple para aquellos intervalos donde el
producto de los dos binomios es negativo por lo tanto la solución viene dada por:
SG 3,5
x R / 3 x 5
Gráficamente:
)
)
-3
5
Casos especiales
1. Si al resolver la inecuación se obtiene una expresión de la forma:
Solución
2
(ax + b) ≥ 0
valor critico
(ax + b)2 > 0
(ax + b)2 ≤ 0
x = − b/a
2
(ax + b) < 0
Ejemplo:
x2 2 x 1 0
x2 2 x 1 0
Usando la fórmula cuadrática :
x 1
2
x
2 22 4 2 0
1
2
2
0
Como un número elevado al cuadrado es siempre positivo la solución es
2. Cuando no tiene raíces reales (discriminante menor que cero), le damos al
polinomio cualquier valor si:
Página
11
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
El signo obtenido coincide con el de la desigualdad, la solución es
El signo obtenido no coincide con el de la desigualdad, no tiene solución
(vacio).
Solución
2
x + x +1 ≥ 0
x2 + x +1 > 0
x2 + x +1 ≤ 0
x2 + x +1 < 0
INECUACIONES DE GRADO SUPERIOR
Pasos:
1.
2.
3.
4.
5.
Se descomponen en factores de primer o segundo grado.
Se obtienen los ceros de cada factor representándolos en rectas distintas.
Se estudia el signo de cada uno de los intervalos formados.
En una nueva recta se llevan todos los ceros, aplicando la regla de los signos.
Se ve cuales de los intervalos son solución de la inecuación.
Ejemplo:
Resolver la inecuación x 3 4x 0
Resolverla es buscar los valores de la x que hacen que el miembro de la izquierda sea negativo
(<0).
El procedimiento más sencillo consiste en factorizar el polinomio (en este caso podemos sacar
factor común x)
x x 2 4 0 , o lo que es lo mismo x x 2 x 2 0
Tenemos tres valores de x (el 0, 2, -2) que hacen que ese producto valga cero, los restantes
valores de la x harán que ese producto sea distinto de 0, bien positivo o negativo.
El estudio es el mismo que antes, dibujamos y señalamos sobre la recta real los valores que hacen
cero el producto y vamos tomando valores de x y se sustituye en la ecuación inicial para ver el
signo de la operación. Observa la gráfica:
_
+
-2
_
0
Los valores de la x que hacen negativo el producto son
+
2
,2 0,2 .
3. INECUACIONES RACIONALES
Son inecuaciones racionales, aquellas en las que tanto el numerador como el denominador son
inecuaciones polinómicas.
Página
12
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Expresión general: son del tipo
ax b
cx d
etc.… y de grados mayores que uno.
0 , o todas sus equivalentes
ax b
cx d
0, o
ax b
cx d
0,
Se resuelven de un modo similar a las de segundo grado, pero hay que tener presente
que el denominador no puede ser cero . Estos tipos de problemas pueden ser resueltos
usando el método analítico o el método gráfico.
Pasos:
1º Hallamos las raíces del numerador y del denominador.
2º Representamos estos valores en la recta real, teniendo en cuenta que las raíces del
denominador, independientemente del signo de la desigualdad, tienen que ser
abiertas.
3º Tomamos un punto de cada intervalo y evaluamos el signo en cada intervalo
4º La solución está compuesta por los intervalos (o el intervalo) que tengan el
mismo signo que la fracción polinómica.
Ejemplo:
1. Dada la siguiente inecuación
x 2 3x 10
0 halle el conjunto solución y grafique.
x2 x 2
Factorizando los polinomios dados:
x2 3x 10 x 5 x 2 ,
x2 x 2 x 2 x 1
Resultando una inecuación de la forma:
x 5 x 2 0
x 2 x 1
Las raíces que anulan el numerador son x 5 y x 2 , y las que anulan el denominador son
x 2 y x 1 , las cuales se ubican sobre la recta real. Se le asignan valores arbitrarios a x en
cada intervalo, y se determinan los signos de la desigualdad.
Página
13
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Se observa en el cuadro anterior que la desigualdad se cumple para aquellos intervalos donde el
cociente es negativo, debido a que la inecuación original es < 0 (es negativa) por lo tanto la solución
viene dada por:
SG 5, 2 1, 2
Gráficamente:
2. Resolver
x 1
x 1
x 1
x 1
(
)
(
)
-5
-2
1
2
1
1 0 , ojo, si pasamos multiplicando el denominador al otro miembro estaríamos
cometiendo un error. Resuelve por tu cuenta la inecuación x 1 x 1 y compara los resultados.
Para nuestro caso, operando
x 1
x 1
1 0
x 1 x 1
x 1
2
x 1
0 , y todo se reduce a
averiguar cuál es el signo del denominador, cuándo éste es negativo, y lo es en ,1 .
4. INECUACIONES CON VALOR ABSOLUTO
RECORDEMOS:
El valor absoluto nos permite considerar una magnitud numérica sin tener en cuenta el signo. Su
definición formal es:
a para a 0
a
, a R
a para a 0
y significa que el valor absoluto de un número nunca es negativo.
Página
14
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Ejemplo: 5 5 5
Propiedades del valor absoluto
La solución de ecuaciones e inecuaciones con valor absoluto requieren del conocimiento y dominio
de algunas propiedades fundamentales que guíen los procesos. A continuación se dan las
propiedades que serán usadas en el tema en cuestión.
Sean a, b R.
1.
a 0
2.
a2 a
3.
a a
4.
a
5.
a b a b
6.
a
b
2
a2
a
b
, si b 0
7.
a b a b Desigualdad triangular
8.
a b
b0
a b
a b
Desigualdades con valor absoluto
Sea x, y, a R . Se tiene entonces:
1. x a sii a 0 x a x a ó a x a
[
]
-a
a
2. x a sii x a x a
]
-a
3. x y
[
a
sii x 2 y 2
Inecuaciones de primer grado con valor absoluto
Son aquellas en las que parte de la inecuación, o toda ella, viene afectada por el valor absoluto de
la misma.
Para resolver estas inecuaciones es suficiente con desarrollar el valor absoluto de acuerdo a los
teoremas antes mencionados, para luego aplicar los conocidos métodos de resolución de
inecuaciones.
Las inecuaciones de primer grado con valor absoluto pueden presentar las siguientes formas:
Página
15
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Sean x, a, b, c R .
1)
ax b c
ax b c
y
ax b c
ó
c ax b c
Ejemplos:
a) Encuentre el conjunto de soluciones que satisface: 5 x 10 15 y grafique.
Aplicando la propiedad de las desigualdades con valor absoluto, obtenemos:
15 5 x 10 15
15 10 5 x 10 10 15 10
25 5 x 5
25 5 x 5
5
5 5
5 x 1
[
]
-5
1
S 5,1 x R / 5 x 1
b) Encuentre el conjunto de soluciones que satisface:
x
2< 1
3
x
3 < < 1
3
x
3 3 < 3< 1 3
3
9 < x < 3
1 <
2)
ax b c
x
2 < 1 y grafique.
3
(
)
-9
-3
S 9, 3 x R / 9 < x < 3
ax b c
ó
ó ax b c ax b c
ax b c
Ejemplos:
a) Encuentre el conjunto de soluciones que satisface: 3x 8 2 y grafique.
Página
16
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
3x 8 2
3x 2 8
3 x 8 2
3 x 2 8
3x 10
3 x 6
6
3
x 2
x
x
10 3
10
3
5 x 3< 7
5 x >7+3
5 x < 7+3
5 x >10
5x< 4
x >10 5
x < 4 5
2
, 10 3 2,
b) Encuentre el conjunto de soluciones que satisface:
5 x 3>7
-2
4
5 x 3 < 7 y grafique.
)
(
5
2
4
, 2,
5
x >2
Otro ejemplo
Resolvamos la desigualdad
2x 1
3
x3
Utilizando la propiedad (6) del valor absoluto, tenemos la siguiente cadena de desigualdades
equivalentes:
2x 1
3
x3
2x 1 3 x 3
2 x 1 3x 9
2
2
2 x 1 3x 9 0
2 x 1 3x 9 2 x 1 3x 9 0
x 10 5x 8 0
2
2
Elaborando un diagrama de signos tenemos
x 10
Signo de 5 x 8
Signo de x 10 5 x 8
Signo de
+
─
─
─
─
+
─
+
─
8
Vemos que la solución de la desigualdad es 10,
5
Página
17
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Problemas que se resuelven por medio de inecuaciones
Las inecuaciones permiten resolver problemas. Veamos el siguiente ejemplo.
Ejemplo: Una camioneta pesa 875 kg. La diferencia entre el
peso de la camioneta vacía y el peso de la carga que lleve no
debe ser inferior que 415 kg. Si hay que cargar cuatro cajones
iguales, ¿cuánto puede pesar, como máximo, cada uno de ellos
para poder llevarlos en ella?
En primer lugar, traducimos el enunciado al lenguaje simbólico, llamamos x al peso de cada cajón
y planteamos la siguiente inecuación:
Peso de la furgoneta − peso de 4 cajones
875 − 4. X
no es menor que 415 kg
415
Una forma de resolver la inecuación es seguir los siguientes pasos:
Restamos 875 a ambos miembros de la desigualdad
- 4. x 415 - 875
Hacemos el cálculo en el segundo miembro
- 4. x - 460
Para despejar x , multiplicamos a ambos miembros por
1
4
(Cuidado: como multiplicamos por un número negativo,
debemos cambiar el sentido de la desigualdad)
1
x 460
4
x 115
Hacemos el cálculo
Esto significa que el peso de cada cajón no podrá superar los 115 kg. Además, como se trata de un
peso, x > 0.
Entonces, la solución está formada por todos los números reales pertenecientes al intervalo
(0, 115]. Graficamos la solución en la recta real:
Funciones de variable Real
Página
18
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Definición de función
Una función f es una regla de correspondencia que asigna a cada elemento x de un conjunto A
llamado dominio un valor único f(x) de otro conjunto B. El subconjunto de B formado por todos los
elementos y a los que se les asigna elementos de A se llama rango o recorrido de la función, y
cada uno de sus elementos se llama imagen.
Representemos en un diagrama de flechas una relación que es función y una que NO es función
Ahora representemos en el plano cartesiano una relación que no es función.
Si una gráfica contiene los puntos (a, b) y (a, c) entonces dicha gráfica no representa una función,
ya que a un valor del dominio le corresponden dos valores del rango.
Observe el dibujo:
Las funciones se representan mediante ecuaciones de la forma y = f(x), por ejemplo:
y f ( x) x 2
;
y g ( x) 3x 2 x
y j ( x) x 6
;
y t ( x)
x2
x4
Página
19
x 1
x 3
;
y h( x )
;
y k ( x) sen( x)
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Por otra parte en las funciones del tipo y=f(x), la relación entre ambas variables x e y está
claramente determinada. Por ese motivo la expresión y=f(x) recibe el nombre de forma explícita de
la función. Sin embargo, en algunas ocasiones la relación entre las variables de la función no viene
expresada de una forma tan clara sino a través de una ecuación que las liga, como por ejemplo:
Podemos decir que esta manera de representar una función recibe el nombre de forma implícita
de la función.
La relación entre ambas variables viene dada por una ecuación en la que hay que despejar la
variable dependiente para poder encontrar la relación entre ambas. Cuando nos encontramos con
una expresión implícita hay que tener un poco de cuidado, pues no vale cualquiera. De hecho, una
de las anteriores expresiones no corresponde a una función. ¿Sabrías decir cuál es y por qué?
Dibujar las cuatro expresiones anteriores puede servirnos de ayuda.
Gráfica de una función
La gráfica de una función f es el conjunto de todos puntos (x, f(x)) en el plano xy, tal que
restringimos los valores de x al estar en el dominio de f.
El siguiente diagrama muestra la gráfica de una función:
Prueba de la recta vertical
Para que una gráfica sea la gráfica de una función, cada recta vertical debe intersecarse con la
gráfica en un solo punto.
Ejemplo
Para obtener la gráfica de f(x) = 3x2 - 4x + 1 con dominio restringido a [0, + ∞), sustituimos f(x)
por y, y obtenemos la ecuación y = 3x2 - 4x + 1.
Entonces obtenemos la gráfica por medio de trazado de puntos, donde restringimos a x al estar en
[0, + ∞), y obtenemos el siguiente dibujo:
No hay nada a la izquierda del eje-y, pues hemos restringido a x al estar ≥ 0.
Elementos de una función
Página
20
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Los dos principales elementos de una función son los posibles valores que pueden tomar ambas
variables (dependiente e independiente).
Se llama Dominio de una función al conjunto de valores que puede tomar la variable
independiente (x) de manera que la expresión dada tenga sentido en los números Reales.
El dominio de una función del tipo y=f(x) suele representarse con alguna de estas
expresiones: D (f), Dom (f).
Se llama Recorrido, Rango o Imagen de una función al conjunto de valores que puede
tomar la variable dependiente, es decir, es el conjunto de valores que puede alcanzar la
función. El recorrido de una función del tipo y=f(x) suele representarse con alguna de estas
expresiones: R (f), Rango (f), Im (f).
Dominio de algunas funciones
1. Dominio de las funciones polinómicas
Definición:
Una función polinómica es de la forma:
f ( x) an x n an1 x n1 an2 x n2 .... a1 x a0 , donde n Z+
Ejemplos: f ( x) 2 x2 3x 2
g ( x) x3 2 x2 x 2
;
h( x) 2 x 5
;
Notación: Dominio de f (x) se escribe: Domf(x)
El dominio de una función polinómica es el conjunto de los números reales (R): Domf(x)=R
2. Dominio de las funciones racionales
Definición:
Una función racional es el cociente de dos funciones polinómicas (polinomios). Ejemplos:
f ( x)
2x 3
x 2 1
;
g ( x)
x4
2x x 4
;
2
Una expresión de números reales de la forma
h( x )
x
x x
4
A
no existe si B =0, de manera que para hallar el
B
dominio de una función racional basta con igualar el denominador a cero y determinar así los
únicos valores de x que no pertenecen al dominio (valores críticos del denominador).
El dominio de una función Racional es el conjunto de los números reales (R) diferentes de los
valores críticos del denominador (V.C.D): Dom f(x) = ℛ − {V.C.D}
Ejemplo:
Hallar el dominio de la función f ( x)
2x 3
x 3x 2
2
Página
21
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Igualamos el denominador a cero: x 2 3x 2 0
Factorizamos: ( x 2)( x 1) 0 este producto es cero si uno de sus factores es cero, así:
x 2 0 , entonces: x = - 2
x 1 0 , entonces: x = - 1
De lo anterior, deducimos que los números – 2 y 1 no pertenecen al dominio y por lo tanto:
Domf(x)= ℛ − {-2,-1}
3. Dominio de funciones con radicales
f ( x) x 1
Primer caso:
La expresión que define a esta función tiene validez en R solamente si el radicando es mayor o
igual que cero, es decir, x 2 1 0 al resolver la inecuación se obtienen los valores que pertenecen
al dominio.
2
x2 1 0
( x 1)( x 1) 0
Al resolver la inecuación se obtiene , 1 1, , entonces:
Segundo caso:
g ( x)
Dom f ( x) , 1 1,
x
x4
En este caso es necesario asegurar que el denominador no sea cero ( x 4) , y además que el
radicando sea mayor que cero ( x 4 0 ), de tal manera que debemos resolver la ecuación:
x40
Domg(x)= (4, )
x2
x4
En este caso debemos controlar tanto lo que sucede en el numerador como lo que sucede en el
denominador, es decir:
Tercer caso:
-
h( x )
x20, x 2
El radicando debe ser positivo o cero.
El denominador debe ser distinto de cero. x 4
Observemos sobre una recta numérica esta situación:
De manera que la solución es: Domh(x) = [2,4) (4, )
Recorrido o rango de algunas funciones
Algunas funciones permiten hallar de manera sencilla sus recorridos.
Página
22
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Por ejemplo
Hallar el recorrido de la función y t ( x)
2x 1
x5
Para lograrlo despejamos x:
y ( x 5) 2 x 1
xy 2 x 5 y 1
x
xy 5 y 2 x 1
x( y 2) 5 y 1
5y 1
y2
Entonces, en la última ecuación y debe ser distinto de 2, es el único valor que no pueden tomar las
imágenes, por lo tanto la solución es:
R ango {2}
Intersecciones con los ejes
Un punto (a, 0) es una intersección de la gráfica de f con el eje x si f (a) 0 , es decir, si este
punto es una solución de la ecuación que define a f. Por lo tanto, para hallar la intersección de la
gráfica con el eje y debemos hacer x = 0 y resolver la ecuación que se obtiene.
Un punto (0, b) es una intersección de la gráfica de f con el eje y si f (0) b es decir, si este punto
es una solución de la ecuación que define a f. Por lo tanto, para hallar la intersección de la gráfica
con el eje x debemos hacer y = 0 y resolver la ecuación que se obtiene.
Nota: Las intersecciones con los ejes se llaman interceptos.
A continuación se muestran algunos dibujos para ilustrar lo que hemos afirmado anteriormente:
Ejemplo
Halle los interceptos de la función y
2x 2
x7
Página
23
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
2
7
2x 2
→ Hacemos y = 0, entonces: 0
por lo tanto 2 x 2 0 y
x7
1. Intersección con el eje y →
2. Intersección con el eje x
Hacemos x = 0, entonces: y
obtenemos que: x = - 1
Simetrías de una función
Al igual que el conocimiento de las propiedades anteriores, el hecho de saber si la gráfica de una
función presenta algún tipo de simetría nos permitirá conocer los valores que toma la función en
determinada zona sin más que conocer los valores de la misma función en la zona simétrica. Una
función puede presentar diferentes tipos de simetría, o ningún tipo en absoluto. De todos los
posibles tipos de simetría que pueden presentarse hay dos que son fácilmente detectables y es en
esos dos tipos en los que vamos a centrar nuestro estudio.
Una función
es:
a. Simétrica respecto al eje Y si
; se dice que f(x) presenta simetría par.
b. Simétrica respecto al origen de coordenadas si
; se dice que f(x) presenta
simetría impar.
Veamos los siguientes ejemplos
1. Simetría con el eje y
2. Simetría con el origen
Funciones par e impar
Sea f una función, entonces:
a. f es par si satisface f (-x) = f(x)
b. f es impar si satisface f (-x) = - f(x)
Página
24
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Ejemplos:
La función f(x)= x2 es par, veamos: f ( x) ( x)2 x 2 f ( x) por lo tanto es par.
La función f ( x) x3 es impar, veamos: f ( x) ( x)3 x3 f ( x) por lo tanto es impar.
Álgebra de funciones
Definimos las operaciones básicas entre funciones así:
SUMA: ( f g )( x) f ( x) g ( x)
DIFERENCIA: ( f g )( x) f ( x) g ( x)
PRODUCTO: ( f .g )( x) f ( x).g ( x)
COCIENTE:
f
f ( x)
, g ( x) 0
( x)
g ( x)
g
Nota:
En cada uno de los casos anteriores, el dominio de la función resultante, es la intersección de los
dominios de f y g. En el caso particular del cociente se deben excluir de la intersección los valores
de x que anulen el denominador g.
Ejemplo:
Dadas f ( x) x 2 x, g ( x)
3
1
. Determinar f g , f g , f g y los dominios
x
En primer lugar es necesario determinar el dominio de cada función:
Dom g 0 (Porque no se puede dividir por cero)
Dom f (Es un polinomio);
Realicemos las operaciones:
4
2
2
1 x 2x 1 x 1
f ( x) g ( x) x 2 x
x
x
x
Dom( f g ) Dom f Dom g 0
3
2
4
2
1 x 2x 1
f ( x) g ( x) x 2 x
x
x
Dom( f g ) Dom f Dom g 0
3
3
1 x 2x 2
f ( x) g ( x) x 3 2 x
x 2
x
x
Dom( f g ) Dom f Dom g 0
Función a trozos
Hasta ahora hemos visto cómo las funciones, sean del tipo que sean, suelen admitir una expresión
del tipo y = f(x). Hemos visto también que es especialmente interesante (pues facilita la obtención
de información) que la expresión f(x) sea de tipo matemático. Hasta ahora hemos trabajado con
expresiones simples como por ejemplo:
Página
25
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
x2
3 2x
y x 2 3x 2
2x 3
y
y 3 25 x 2
3
x4
Sin embargo, con mucha frecuencia, las expresiones analíticas que aparecen en las Ciencias
Sociales no admiten una única formulación para todos los valores de la variable independiente, de
manera que es necesario utilizar diferentes fórmulas para la función según los distintos valores de
x. De este tipo de funciones se dice que están definidas a trozos.
Una función a trozos es aquella en la que se usan “trozos” de funciones para conformar una nueva
función, por ejemplo la función valor absoluto se puede considerar como una función a trozos,
veamos:
y
x si x 0
x 0 si x 0
x si x 0
Otros ejemplos
x
1. f ( x) x 2
1
si x 0
si 0 x 1
si x 1
si x 2
x
si 2 x 3
2. g ( x) 1
2 x 5 si x 3
Movimientos en el plano
Página
26
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Translación Vertical
La ecuación y k f ( x), k una constante real describe una traslación vertical de y = f(x) de k
unidades.
Si k > 0, la traslación es hacia arriba.
Si k < 0, la traslación es hacia abajo.
Ejemplo
y x 1
Translación Horizontal de y = f(x+h) de h unidades.
Si h > 0, la traslación es hacia la derecha.
Si h < 0, la traslación es hacia la izquierda.
Ejemplo
y
x 1
Página
27
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Gráficas de funciones básicas
Existen algunas funciones que son de uso común en el desarrollo de los cursos de cálculo,
entre ellas tenemos:
1.
Función Lineal: f ( x) ax b
2.
Función Cuadrática: f ( x) ax 2 bx c
3.
Función Cúbica: f ( x) ax 3 bx 2 cx d
4.
Función Raíz Cuadrada: f ( x)
5.
Función Valor Absoluto: f ( x) x
x
1
x
7. Función logarítmica f ( x) Log a ( x)
6.
Función Racional: f ( x)
8.
Función exponencial f ( x) a x
9.
Función logística
f ( x)
a
b e c x
10. Función seno f ( x) senx
11. Función coseno f ( x) cos x
A continuación trazamos las gráficas de algunas de estas funciones:
1. Función lineal
f ( x) x (Función identidad)
Ejemplo: f ( x) 2 x 1
2. Función cuadrática
f ( x) x 2
Ejemplo: f ( x) x 2 1
Página
28
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
3. Función cúbica
f ( x) x 3
Ejemplo: f ( x) 2 x 3 1
4. Función raíz cuadrada
f ( x) x
Ejemplo: f ( x)
x 2
5. Función valor absoluto
Página
29
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
f ( x) x
Ejemplo: x 1 2
6. Función Racional
1
f ( x)
x
7. Función logarítmica
f ( x) Log a ( x)
a>0
0<a
Página
30
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
8. Función exponencial
f ( x) a x
Composición de Funciones o Función compuesta
En general, dadas dos funciones f ( x), g ( x)
x
f(x)
g
º
g[f(x)]
f
La función g f es la función compuesta de f y g, que transforma x en g [f(x)]
Se debe tener cuidado con los dominios de g f y de f g . El dominio de g f es la parte del
dominio de f, para los cuales g acepta a f(x) como pre-imagen.
También, el dominio de f g es la parte del dominio de g para los cuales f acepta a g(x) como preimagen.
Ejemplo
Si f y g son las funciones definidas por:
f ( x)
Entonces:
x 3
2
g
y
g ( x) x
f x g f x
f ( x)
x 3
2
g ( x) 3
x 3
2
2
Del ejemplo anterior se deduce fácilmente que en general:
g f ( x ) f g ( x)
f
g x f g x
Se debe tener también cuidado con los dominios de g f y de f g . El dominio de g f es la
parte del dominio de f, para los cuales g acepta a f(x) como pre-imagen.
Esto es, D (f) = ℛ
Página
31
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Ahora, como g, solo acepta reales positivos de f(x), esto es, valores de x para los cuales:
f ( x) 0
x 3
0 x3
2
Se concluye entonces que: D (g o f) = [3, +
Nótese que g f
)
1 g f 1 g 1
Igualmente, g f
2 g f 2
NO ESTA DEFINIDO.
2
g 1
NO ESTA DEFINIDO.
También, el dominio f g es la parte del dominio de g para los cuales f acepta a g(x) como preimagen.
Es decir, D (g) = [0, +
).
Ahora, como f acepta cualquier valor real de g(x), entonces f acepta en particular, los valores de g
en el intervalo D (g) = [0, +
).
De esta forma: D (f o g) = [0, +
).
En el cálculo, a menudo se necesita escribir una función dada como la composición de dos
funciones. Esto puede hacerse de varias maneras.
Así por ejemplo, la función: p( x)
3x 2 5x 2 puede escribirse en las formas:
P(x) = g f ( x) siendo f ( x) 3x 2 5x 2
y
P(x) = g f ( x) siendo f ( x) 3x 5x
g ( x)
2
En efecto, g f
g
x g f x
y
g ( x)
x
x2
g 3x 2 5x 2 3x 2 5x 2 en el primer caso, y
f x g f x g 3x 2 5x 3x 2 5x 2 en el segundo caso.
Función inversa
Dada una función f(x), su inversa es otra función, designada por f -1(x) de forma que se verifica:
Si f(a)=b entonces f -1(b)=a
Propiedades
1. Toda función y su inversa son simétricas a la función identidad ( y x ).
2. La compuesta de una función y su inversa da como resultado la función identidad
f
f 1 ( x) f 1 f ( x) x
3. El dominio de la función inversa es igual al rango de la función directa, y el rango de la función
inversa es igual dominio de la función directa
Página
32
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Dom f 1 ( x) Rango f ( x)
Rango f 1 ( x) Dom f ( x)
4. f 1 ( x)
1
f ( x)
Para que exista la inversa de una función ésta debe cumplir con la condición de ser una función
inyectiva.
Función inyectiva
Definición:
Una función f es inyectiva (uno a uno) si se cumple que:
.
o equivalentemente, x1 x2 f ( x1 ) f ( x2 ); x1 , x2 D( f )
En otras palabras, una función f es 1-1, si para cada x en el dominio f, existe exactamente una y
en el rango, y, ninguna y en el rango es imagen de más de una x en el dominio.
Existe también un criterio sencillo para determinar si la gráfica de una ecuación corresponde a
una función 1-1. Este criterio se conoce como criterio de la recta horizontal.
Criterio de la recta horizontal
Si toda recta horizontal corta a la gráfica de una función f en uno y solo un punto, entonces f es
una función 1-1
Así por ejemplo, en la fig. 1, aparece la gráfica de la función y f ( x) x 2 1 la cual, de acuerdo
al criterio de la recta horizontal no corresponde a una función 1-1.
Figura 1
Figura 2
Nótese que la recta y = 2, corta la gráfica en más de un punto: p1 1, 2 y p2 1, 2
Igualmente, en la fig. 2, aparece la gráfica de la función y f ( x) x3 1 , la cual, de acuerdo al
criterio de la recta horizontal, corresponde a una función 1-1.
Nótese que toda recta horizontal, corta a la gráfica en uno y solo un punto.
Si Tenemos la función y=f(x), y queremos hallar su inversa, seguimos los siguientes pasos:
1) Se intercambian la x y la y en la expresión inicial: y=f(x)
2) Se despeja la y en la nueva expresión x = f (y)
Página
33
x=f(y)
-1
y=f (x)
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Ejemplo:
Hallar la inversa de y=2x
1) Cambiamos la x por la y, nos queda entonces x=2y
x
2
x
Por tanto la función inversa de y=2x es y
; es decir f
2
2) Despejamos la y, nos queda entonces y
1
( x)
x
CIONES ODELOS
2
MATEMÁTICOS:
Modelos matemáticos: construcción de funciones
Modelar una situación matemáticamente significa representarla en términos matemáticos. La
representación particular que se usa se llama un modelo matemático de la situación.
1. Modelos lineales de costo, ingreso y utilidad
a. Una función costo especifica el costo C como una función de la cantidad de artículos x. En
consecuencia, es el costo de x artículos, y tiene la forma
Costo = Costo variable + Costo fijo
en la que el costo variable es una función de x y el costo fijo es constante. Una función costo de la
forma C(x) = mx + b se llama una función costo lineal; el costo variable es mx y el costo fijo
es b. La pendiente m, es el costo marginal, mide el costo incremental por artículo.
b. Una función ingreso específica el ingreso I(x) que resulta de la venta de x artículos.
El ingreso que resulta es
I = p . x (Precio por número de unidades).
c. Una función utilidad especifica la utilidad (ingreso neto) U(x) que resulta de la venta
de x artículos. Las funciones costo, ingreso y utilidad se relacionan con la formula
U(x) = I(x) - C(x).
El equilibrio ocurre cuando P(x) = 0, es decir, cuando
R(x) = C(x).
Ejemplo
Si el costo fijo es $400, y si el costo marginal es $40 por artículo, y si se vende los artículos a $60
cada uno, entonces cuantos artículos debe vender para alcanzar el punto de equilibrio
Solución
C(x) = 40x + 400
I(x) = 60x
U(x) = R(x) - C(x)
= 60x - (40x + 400)
= 20x - 400.
Para el equilibrio, U(x) = 0
20x - 400 = 0,
Página
34
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Entonces x = 20. Por lo tanto, tiene que vender 20 artículos para alcanzar el equilibrio.
2. Modelos demanda y oferta
Una función (de) demanda expresa la demanda q (el número de artículos solicitados) como una
función del precio unidad p (el precio por artículo).
Una función de oferta expresa la oferta q (el número de artículos que un proveedor está dispuesto
a llevar al mercado) como una función del precio unidad p (el precio por artículo). Es normalmente
el caso que la demanda disminuye y la oferta sube a medida que el precio sube.
Una función lineal (de) demanda tiene la forma q = m .p + b, donde q es la demanda (número de
artículos vendidos) y p es el precio por artículo. Se puede construir una ecuación demanda lineal a
saber la demanda a dos precios distintos
La demanda y la oferta están en equilibrio cuando son iguales. Los valores correspondientes
de p y q se llaman precio de equilibrio y demanda de equilibrio. Para hallar el precio de
equilibrio, determine el precio unitario p donde se cruzan las curvas de demanda y oferta (a veces
podemos determinar este valor analíticamente por igualar las funciones de demanda y oferta y
despejar a p). Para hallar la demanda de equilibrio, evalúe la demanda (o oferta) con el precio en
equilibrio.
Ejemplo
Si se vende 100 camisetas por semana cuando el precio es $10, y 200 por semana cuando se baja
el precio hasta $8, entonces la ecuación (lineal) demanda es
q = -50p + 600 Ecuación de la recta por (10, 100) y (8, 200)
Entonces, la función ingreso relacionada es
R = p. q = p (-50p+600)
= -50p2 + 600p.
Otros ejemplos
Ejemplo 1
A un tanque que tiene la forma de un cono circular recto invertido de 4 metros de radio y 16 metros
de altura entra agua a una razón determinada.
Expresar el volumen de agua en un instante dado:
a. En función de la altura h.
Página
35
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
b. En función del radio de la base x.
Solución
En la figura aparece el cono con las dimensiones dadas y una porción del volumen en el instante
determinado.
El volumen del agua en el instante determinado viene dado por:
1
Vc (area base)(altura)
3
1
V r 2h
3
(1)
Como los triángulos ODE y OBC son semejantes, se tiene:
16 h
h 4x
4
x
(2)
a. Si se quiere expresar el volumen en función de la altura h, se debe despejar x en (2) y sustituirlo
en (1). Así,
x
Luego,
2
h
4
V
→
1 h
V h
3 4
1
h3
48
b. Para expresar el volumen en función del radio x, se sustituye (2) en (1).
Así:
1
4
V x 2 (4 x) x3
3
3
Ejemplo 2
Se dispone de una cartulina cuadrada de lado a y se quiere hacer una caja sin tapa recortando
cuadrados iguales en las esquinas y doblando sus lados (Ver fig.). Exprese el volumen de la caja en
función del lado del cuadrado recortado.
Página
36
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Solución
Volumen de la caja = Área de la base x altura
V ( x) a 2 x . x
2
V ( x) 4 x3 4ax 2 a 2 x
0 x
a
2
Ejemplo 3
Una piscina rectangular de 20 mts. de largo por 10 mts de ancho, tiene 4 mts de profundidad en un
extremo y 1 mt en el otro. La figura adjunta ilustra una vista transversal de la piscina. El agua para
llenar la piscina es bombeada por el extremo profundo.
a. Determine una función que exprese el volumen V de agua en la piscina como función de su
profundidad x en el extremo profundo.
b. Calcular V (1) y V (2)
Solución
a. Sea L la longitud de la medida del nivel del agua desde el extremo profundo hasta el menos
profundo.
Note que L y x son los lados de un triángulo rectángulo semejante al triángulo cuyos lados son 20 y
3 mts.
De esta forma, se puede establecer la siguiente proporción:
Página
37
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
L 20
20
L
x , con 0 x 3
x
3
3
Ahora, el volumen V en un instante determinado viene dado por:
V = (Área de la sección transversal). (Ancho)
20
x.x
L.x
100 2
3
V
.10
.10
x
2
2
3
V ( x)
b.
100 2
x
3
V (1)
100 2 100
33.3 m3
1
3
3
V (2)
100 2 400
133.3 m3
2
3
3
Página
38
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
UNIDAD 2
LÍMITES Y CONTINUIDAD DE FUNCIONES
Límite de funciones
Conceptos básicos
Pretendemos esclarecer la idea de límite de una función. Haremos hincapié en el concepto, pues el
cálculo matemático requiere el conocimiento de diversas herramientas que no entraremos a contar
en detalle, utilizando algún programa de cálculo para ello.
Para entender el concepto de límite veámoslo con un ejemplo.
Consideremos la función:
f ( x)
x 1
x 1
cuyo conjunto de definición (dominio) es el conjunto de los números reales no negativos excepto
x=1, es decir: D x / x 0, x 1
Si realizamos su representación gráfica:
Para x=1, el dibujo hace un pequeño salto, que no se aprecia en la figura pero que sería tal y como
puede verse a continuación:
Página
39
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Como veremos en el apartado siguiente ello implicará una discontinuidad de la función en x = 1.
Ahora nos preguntamos: cuando el valor de x es muy cercano a 1, ¿cuánto vale la función?
Es claro que en x =1 la función no está definida; por lo tanto, tendremos que dar un método que sea
capaz de responder a la cuestión anterior, la cual podemos plantearla en los términos siguientes: Si
x tiende a 1 ¿a cuánto tiende la función?
A esto es lo que llamaremos límite de la función F(x) cuando x tiende a 1 y lo denotaremos como:
lim f ( x) L
x1
Definición informal de límite
Sea f(x) una función, si las imágenes se aproximan suficientemente a un valor L, cuando los
valores de x se aproximan suficientemente a un valor b, decimos que el límite de f(x) cuando x
tiende a b es igual a L y escribimos: lim f ( x) L
x b
Siendo L el valor de dicho límite, el cual queremos calcular; para ello, observemos que a la hora de
aproximarnos a lo largo del eje de abscisas al punto x =1 lo podemos hacer por la derecha y por la
izquierda, es decir, podemos considerar (siempre para puntos cercanos a 1). A estos límites los
llamaremos límites laterales.
Límites laterales
lim f ( x) , se llama límite lateral por la derecha.
xb
lim f ( x) , se llama límite lateral por la izquierda
xb
Para que el límite exista debe cumplir que el límite por la izquierda y por la derecha sean iguales,
de lo contrario diremos que el límite no existe en dicho punto, es decir:
lim f ( x) L , si y solamente si: lim f ( x ) = lim f ( x)
x b
x b
x b
Ejemplo 1
Sea
4 x si x 1
f ( x)
Hallar lim f ( x)
2
x1
4 x x si x 1
Página
40
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Solución:
lim f ( x) lim (4 x) 4 1 3 (Acercamiento por la izquierda)
x 1
x 1
lim f ( x) lim (4 x x 2 ) 4 1 3 (Acercamiento por la derecha)
x 1
x 1
Entonces: lim f ( x) 3
x 1
Ejemplo 2
Determinar, si existe, el límite de la siguiente función en los puntos x = 2 y x = 0:
f ( x)
x 1
x 1
Solución:
Calculemos:
lim f ( x)
x 2
Si determinamos el valor de la función en dicho punto tenemos:
f (2)
1
1 2
y podemos observar en la gráfica de la función como existen los límites laterales:
lim f ( x) lim f ( x)
x 2
x 2
1
1 2
con lo cual tenemos que:
lim f ( x)
x 2
1
1 2
Para el segundo punto, calculemos:
lim f ( x)
x 0
Página
41
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
En este caso, los límites laterales no coinciden, ya que no existe el límite lateral por la izquierda
de la función (no podemos evaluar f en puntos a la izquierda de cero). El límite lateral por la
derecha si existe y vale:
lim f ( x) 1 , por lo tanto el límite pedido no existe.
x 0
En general, para que una función posea en un punto un límite, dicho punto ha de ser tal que puntos
a su izquierda y a su derecha han de pertenecer al dominio de la función. Además, la función no
tiene porqué existir en dicho punto.
Ejemplo 3
Definir una función que NO posea límite en un punto interior a su dominio de definición.
Consideremos, por ejemplo, la función:
Representémosla gráficamente:
En este ejemplo el dominio es todos los números reales ℜ. Si tomamos x=0, que es punto interior,
en él, existe la función y vale f (0) = 0
No obstante, no existe el límite cuando x tiende a cero, ya que los límites laterales no coinciden (por
la izquierda toma el valor cero y por la derecha el valor −∞, como observamos en la gráfica).
Obsérvese que a la hora de calcular los límites laterales utilizamos x2 cuando determinamos el
límite por la izquierda y Log(x) cuando calculamos el límite por la derecha.
Nota:
Sabemos que “el infinito” no es un número, sino un símbolo que expresa un número muy grande,
de tal manera que cualquier otro número real verifica ser menor que él.
Cuando se define el límite como un número real, si en el cálculo de dicho límite no se obtiene un
número real (el infinito no lo es) resultará que el límite no existe. En los dos ejemplos siguientes
puede observar dos casos en los que el límite no existe pero que son casos distintos, ya que en el
primero los límites laterales coinciden y valen infinito, mientras que en el segundo los laterales no
coinciden.
Página
42
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
lim
x 0
1
1
1
lim 2 lim 2
2
x
x 0 x
x 0 x
lim
x 0
1
x
lim
x 0
1
x
Viendo la representación gráfica de las funciones se entiende los resultados obtenidos:
F(x) = 1/x2
F(x) =1/x:
Definición formal de límite
Se dice que la función f(x) tiene como límite el número L, cuando x tiende a c, si fijado un número
real positivo ε, mayor que cero, existe un numero positivo δ dependiente de ε, tal que, para todos
los valores de x distintos de c que cumplen la condición |x – c | < δ, se cumple que |f(x) - L| <ε.
lim f ( x) L 0 0 / 0 x c f ( x) L
x a
Ejemplo 1
Utilicemos la definición para demostrar que lim 4 x 5 3
x 2
Como la función está definida en todo intervalo abierto que contiene a 2, entonces podemos utilizar
la definición para hacer la demostración.
Se debe demostrar que para cualquier 0 existe una 0 tal que
Si 0 x 2
entonces
Si 0 x 2
entonces 4 x 8
Si 0 x 2
entonces 4 x 2
Si 0 x 2
entonces x 2
Entonces, si tomamos
4
(4 x 5) 3 (A)
4
se cumple la proposición (A). Esto demuestra que lim 4 x 5 3
x 2
Ejemplo 2
2
Demuestre que lim ( x x 5) 7 utilizando la definición de límite.
x 3
Página
43
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Para hacer la demostración basta con encontrar un tal que:
0 x 3
( x 2 x 5) 7
( x 2 x 5) 7 x 2 x 12 x 4 x 3 <
(1)
Ya que por definición, el lim f ( x) L existe siempre que
xb
0 x c f ( x) L
Para efectos de simplificación, asumimos un valor de =1 y obtenemos:
x 3 1 2 x 4 2 4 x 4 4 4
x4 8
Sustituyendo en (1) se obtiene que 8 < y que < /8; ya que x 3 por definición.
Propiedades de límites
Sean b, c, n, A y B números reales, sean f y g funciones tales que:
lim f ( x) A , lim g ( x) B Entonces:
x c
x c
1. lim b b
2. lim x c
x c
x c
3. lim b. f ( x) bA
4. lim
x c
x c
5. lim
x c
f ( x).g ( x) A.B
7. lim
x c
f ( x) g ( x) A B
f ( x) A
, B0
x c g ( x )
B
x
0 (K es constante)
8. lim
x 0 k
k
0,
n0
10. lim
x x n
6. lim
f ( x) lim f ( x)
x c
k
no existe ()
x 0 x
x
no existe ()
11. lim
x k
9. lim
Cálculo de límites
1. Límites de funciones polinómicas
3
2
Sea f ( x) 3x 2 x x 2 La gráfica de una función polinómica (o polinomio) tiene un trazo
continuo, por lo cual podemos afirmar:
Sea f un polinomio, entonces para cualquier número real c se tiene que lim f ( x) f (c) , es decir,
x c
que el límite en cualquier punto c de su dominio se halla simplemente calculando su imagen.
Ejemplo:
Para la función anterior lim f ( x) 3(1) 2(1) (1) 2 3 2 1 2 8 f (1)
3
2
x 1
Página
44
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
2. Si al evaluar el limite en forma directa (sustituir el valor del punto en la función), se obtiene una
expresión de la forma
convendrá calcular los límites laterales; si son iguales la función
tiene límite, en caso contrario el límite no existe.
Cuando se presenten funciones con valor absoluto o funciones a trozos también es conveniente
calcular los límites laterales.
3. Si al evaluar el limite en forma directa (sustituir el valor del punto en la función), se obtiene una
0
0
0
expresión de la forma , , 0. , 0 , , 1 (indeterminación) entonces debemos realizar
0
procedimientos algebraicos para suprimir la indeterminación.
Nota: Una indeterminación no significa que el límite no exista o no se pueda determinar, sino que la
aplicación de las propiedades de los límites tal como las hemos enunciado no son válidas.
En estos casos hay que efectuar operaciones particulares para resolver cada una de las
indeterminaciones.
Resumen del Cálculo de límites Indeterminados
0
1. Indeterminación
0
Cuando solo aparecen funciones racionales (polinomios en el numerador y denominador), basta
con descomponer factorialmente el numerador y el denominador.
x3 1
Ejemplo lim 2
x 1 x 1
Para eliminar la indeterminación, factorizamos el numerador y el denominador, simplificamos y
resolvemos el límite obtenido, así:
x 2 x 1
x 1 x 2 x 1
x3 1
lim 2
lim
lim
x 1 x 1
x 1
x 1
x 1 x 1
x 1
Por lo tanto lim
x 1
x3 1 3
x2 1 2
En aquellos casos en que aparecen funciones irracionales (radicales), basta con multiplicar y dividir
por la expresión radical conjugada.
Ejemplo 1
x 1
x 1
lim
lim
x 1 2 x 2
x 1 2 x 2
lim
x 1 2.
x 1
x 1
x 1
lim
x1 2. x 1
x 1
1
x 1 4
1
Página
45
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Ejemplo 2 lim
x 0
x 1 1
x
0
por lo cual debemos realizar algún procedimiento
0
algebraico, en este caso multiplicamos numerador y denominador por x 1 1 , es decir, se
Si sustituimos el valor de x=0 se tiene la forma
racionaliza el numerador (por la conjugada) para aplicar el producto notable:
(a b)(a b) a 2 b 2 , y así eliminar la indeterminación
lim
x 0
x 1 1
( x 1 1)( x 1 1)
( x 1) 1
lim
lim
x 0
x 0 x( x 1 1)
x
x( x 1 1)
x
1
1
lim
lim
x 0 x( x 1 1)
x 0 x 1 1 2
2. Indeterminación
En la mayoría de los casos basta con dividir el numerador y denominador por la mayor potencia de
la variable del denominador.
También se pueden utilizar teoremas como:
Sea f(x) una función racional definida por:
f ( x)
a n x n a n1 x n 1 ...... a1 x ao
bm x m bm1 x m1 ...... b1 x bo
a) Si n < m entonces: lim f ( x) 0
x
a
b) Si n = m entonces: lim f ( x) n
x
bm
c) Si n > m entonces: lim f ( x)
x
Ejemplo 1
lim
x
4 x2 x 1
x2 1
Página
46
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Dividimos por la variable de mayor grado del denominador, x
2
2
4x
x 1
1 1
2 2
4 2
2
x lim
x x lim 4 0 0 4 4
lim x 2 x
1
x
x
x 1 0
x
1
1
1 2
2
2
x
x
x
2
4x x 1
Entonces, lim
4
x
x2 1
Ejemplo 2
lim
x
x2 x 3
x
2
lim
x
x
x
3
1
3
2
1
2
x
x
x lim
x
x
x
x
1
x
Entonces,
lim
x
lim
x
1 0
1
1
1
1
x2 x 3
1
x
3. Indeterminación
∎ En la mayoría de los casos basta con efectuar las operaciones indicadas.
Ejemplo
1
x
lim 2
Indeterminación
x2 x 4
x2
Realizamos la diferencia:
x x 2
1
x
2 2
lim 2
lim
lim 2
2
x2 x 4
x2
x2 x 4
x2
x 4
0
Hay que hacer límites laterales:
lim
x 2
lim
x 2
2
2
x 4
2
2
x 4
2
0
2
0
1
x
lim 2
No
x2 x 4
x2
existe
∎ En otros casos, sobre todo en aquellos en que aparecen raíces cuadradas, basta con multiplicar
y dividir por la expresión radical conjugada(es decir, racionalizar).
Ejemplo lim
x
x
x2 x
Página
47
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
lim
x
lim
x
x
x 2 x lim
x2 x2 x
x x x
x2 x
x
x
x
lim
x
2
x
x x x
2
x
x2 x
x2 x
lim
x
x2
x2 x
2
x x2 x
Hemos transformado el límite en otro indeterminado de la forma
que se resuelve dividiendo el
numerador y el denominador entre x, así:
x
x
1
1
1
x
lim
lim
lim
2
2
x x x x
x x
x
2
1
1 1 0
x
x
1 1
2 2
x
x
x
x
1
Por lo tanto, lim x x 2 x
x
2
4. Indeterminación 0
En la mayoría de los casos basta con efectuar las operaciones indicadas.
Ejemplo
1
lim x 3 . 2
0.() Indeterminación
x3
x 9
Realizamos el producto y en este caso llegamos a otra indeterminada del tipo
0
:
0
x 3 0
lim 2
0
x 3 x 9
x 3
1
1
lim
lim
x 3 x 3 x 3
x 3 x 3
6
5. Indeterminación 0 , 00 , 1
∎ Para determinar estos límites tendremos en cuenta que:
f ( x)
g ( x)
e
Ln f ( x ) g ( x )
e
g ( x ) Ln f ( x )
, de donde resulta que:
lim g ( x) Ln f ( x)
lim f ( x) g ( x ) e x a
x a
Pudiendo aparecer otras indeterminaciones, que resolveremos por los métodos anteriores o por
métodos que aprenderemos en temas posteriores.
Si al calcular el límite de la función aparece una indeterminación del tipo 1 debemos tener en
cuenta que: lim 1
x
x
1
1
x
lim
1
x
e =2'71828...
x 0
x
Página
48
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
∎ También para la indeterminación 1 podemos aplicar con mayor facilidad la siguiente igualdad:
lim f ( x) g ( x) e k , donde k lim f ( x) 1 g ( x)
x a
xa
13 x 2
1 x
2
x 0 1 x
2
Aplicar la igualdad anterior a la resolución del siguiente límite: lim
x2
Al reemplazar el valor al que tiende la x nos da de la forma 1 , aplicando la formula, tenemos:
13 x 2
1 x
lim
2
x 0 1 x
2
x2
= 1
ek
1 x2
1 3x 2
k lim f ( x) 1 g ( x) k lim
1
2
2
xa
x 0 1 x
x
2
2
2
2
1 x 1 x 1 3x
2 x 1 3x 2
k lim
lim
´
2
2
x 0
x 0 1 x
1 x2
x2
x
2
2 6 x2
2
2 1 3x
k lim
lim
2
2
2
x 0 1 x
1 x 0 1 x
1
13 x 2
1 x
2
x 0 1 x
2
Entonces, lim
x2
ek e2
Límites trigonométricos
Un límite básico relacionado con la trigonometría es el siguiente:
lim
x 0
sen( x)
1
x
A partir de este resultado podemos resolver límites como:
1.
1 cos( x)
0
x 0
x
x
1
x 0 sen( x )
lim
2. lim
sen(kx)
k
x 0
kx
3. lim
No olvidar que para resolver los límites trigonométricos debemos de conocer también las
identidades trigonométricas
Ejemplo
Calcular lim
t0
t tan t
sent
Solución: Es conveniente convertir la tangente en su correspondiente expresión en términos de
seno y coseno, tenemos:
t tan t
lim
lim
t 0 sent
t 0
sent
cos t
sent
t
Página
49
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
t cos t sent
t cos t sent
t cos t
sent
cos t
lim
lim
lim
lim
t 0
t 0
t 0 cos t sent
t 0 cos t sent
sent
cos t sent
t
1
lim
lim
11 2
t 0 sent
t 0 cos t
t tan t
t
2
1
Entonces obtenemos que lim
Nota: En este ejemplo se utilizó lim
t 0 sent
t 0 sent
Limites infinitos
Asíntotas verticales
Definición 1
Sea f una función definida en ambos lados de a, excepto posiblemente en x = a. Entonces:
lim f ( x) , significa que los valores de f(x) se pueden hacer arbitrariamente grandes (tan
x a
grandes como deseemos) al elegir un x suficientemente cerca de a (pero no igual a a). En estos
casos la gráfica presenta una asíntota vertical en x = a (recta paralela al eje y por la cual no cruza
la gráfica)
Definición 2
Sea f una función definida en ambos lados de a, excepto posiblemente en x = a. Entonces:
lim f ( x) , significa que los valores de f(x) se pueden hacer arbitrariamente negativos (tan
x a
grandes como deseemos) al elegir un x suficientemente cerca de a (pero no igual a a). En estos
casos la gráfica presenta una asíntota vertical en x = a (recta paralela al eje y por la cual no cruza
la gráfica)
Página
50
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Definición 3
La recta x = a se llama asíntota vertical de la función y f (x) si se cumple una de las siguientes
proposiciones:
lim f ( x)
lim f ( x)
x a
x a
lim f ( x)
lim f ( x)
x a
lim f ( x)
x a
lim f ( x)
x a
x a
Limites al infinito
Sea f una función definida en un intervalo (a, ) , entonces lim f ( x) L significa que los valores
x
de f(x) se pueden aproximar a L tanto como deseemos, si escogemos un x suficientemente grande.
Asíntotas horizontales
Definición
La recta y = L se llama asíntota horizontal de la curva y f (x) si se satisface una de las dos
expresiones:
lim f ( x) L
x
o
lim f ( x) L
x
De lo anterior podemos concluir que una función
racional presenta una asíntota horizontal si el grado del numerador es menor o igual que el
grado del denominador.
Página
51
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Ejemplo y
x2 1
x2 1
x2 1
obtenemos como resultado 1, lo cual significa
x x 2 1
si calculamos: lim
que la gráfica tiene un asíntota horizontal en y = 1, veamos esta situación en el siguiente dibujo:
Asíntotas oblicuas
Sea f (x) una función racional, si el grado del numerador es una unidad mayor que el grado del
denominador, entonces la gráfica de f presenta una asíntota oblicua, esta se halla realizando la
división indicada en la función.
Ejemplo
Sea f ( x)
x2 3
2x 4
Esta función tiene una asíntota oblicua, hallémosla:
Asíntota oblicua: y
1
x 1
2
Veamos la gráfica:
Página
52
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
x2 3
x 2 x 4
Nótese que lim
y además
x2 3
x 2 x 4
lim
Teorema del emparedado
Sean f, g, h funciones tales que: f ( x) g ( x) h( x) para todo x c en un intervalo que contiene a
c, supongamos que lim f ( x) lim h( x) L , entonces:
xc
xc
lim g ( x) L
xc
Ejemplo:
1
Demuestre que lim x 2 sen( ) 0
x 0
x
Página
53
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
1
1
Obsérvese que no podemos aplicar que lim x 2 sen( ) lim x 2 . lim sen( ) puesto que el segundo
x0
x
0
x
0
x
x
límite no existe.
1
x
1
x
Como 1 x sen( ) 1 entonces: x x sen( ) x (véase la figura de arriba)
2
2
2
2
1
2
2
Además: lim x lim ( x ) 0 por lo tanto lim x 2 sen( ) 0
x0
x0
x 0
x
Continuidad de una función
Estudiaremos una característica importante de las funciones como lo es su continuidad, tanto en
forma gráfica como de manera analítica.
Intuitivamente, una función es continua en un punto si a pequeños cambios en la variable
independiente, x, se producen pequeños cambios en la variable dependiente, y. Gráficamente, se
observan claramente, pues son gráficas que se dibujan de un trazo, sin levantar el lápiz del papel.
Matemáticamente, la definición es la siguiente.
Definición:
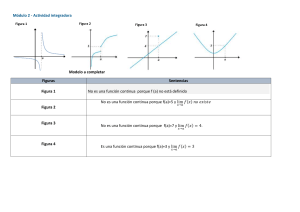
Sea f una función, decimos que f es continua en un punto x = c si se satisfacen tres propiedades:
1. f esta definida en c, es decir, f(c) existe, o , f (c) Dom( f ( x))
2. lim f ( x) existeM
xc
3. lim f ( x) f (c)
xc
El concepto de continuidad en un punto se generaliza a un subconjunto, de forma que se dice que f
es continua en un intervalo abierto (a, b) si es continua en todos los puntos de dicho intervalo.
Además, es continua en un intervalo cerrado [a, b] si es continua en (a, b) y es continua por la
derecha en a y por la izquierda en b.
Podemos observar que en la práctica, el estudio de la continuidad conlleva el cálculo de límites,
cuestión que, como vimos en el apartado anterior, necesitará la ayuda de algún programa de
cálculo.
Cuando una función no es continua en un punto diremos que es discontinua en dicho punto, A
continuación estudiaremos los tipos de discontinuidad.
Clases de discontinuidad
Si cualquiera de las tres condiciones de Continuidad falla decimos que la función es Discontinua.
a. Discontinuidad evitable
Una función tiene una discontinuidad evitable en un punto cuando existe límite en él y no coincide
con el valor de la función en el mismo. Graficamente se reconoce esta discontinuidad si la función
posee un hueco o un quiebre.
El valor que deberíamos dar a la función en dicho punto para que fuera continua en él se llama
verdadero valor de la función en el punto.
Página
54
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
En este caso la función se puede redefinir para que sea continua, es decir la discontinuidad se
puede reparar. Toda función Discontinua evitable es Reparable.
Para evitar la discontinuidad de la función definimos una nueva a partir de la que tenemos, de la
siguiente manera:
f ( x)
g ( x)
L
si x a
, es decir, definimos la nueva función igual que la función que tenemos en
si x a
todos los puntos donde no hay problema y en el punto donde presenta la discontinuidad le
asignamos el valor del límite.
Ejemplo:
x 2 5x 6
Hallar el verdadero valor de la función f ( x )
en el punto x = 3.
x3
Si observamos la función, resulta que no está definida en el punto x = 3, pero si calculamos el límite
de la función en ese punto, obtenemos:
lim
x 3
x2 5x 6
( x 3) ( x 2)
lim
lim( x 2) 3 2 1 que sería el verdadero valor de la función
x 3
x 3
x 3
x 3
en ese punto. La nueva función
x 2 5x 6
g (x ) x 3
1
si x 3
, sería continua en el punto x = 3.
si x 3
b. Discontinuidad no evitable o esencial
Una función tiene una discontinuidad inevitable en un punto cuando no existe límite de la función
en dicho punto.
En este caso, debido a la imposibilidad de hacerla continua decimos que la discontinuidad es
Irreparable.
Graficamente se reconoce esta discontinuidad si la funcion presenta un Salto o separación.
Nota: debe observarse que para clasificar una discontinuidad en una función, es de primordial
importancia el cálculo del límite de la función puesto que si éste existe la función se puede reparar
(evitable); en cambio, si no existe, la discontinuidad es irreparable (esencial).
Ejemplos
Mostramos tres ejemplos de funciones discontinuas, en las cuales fallan las condiciones 1), 2) y 3)
mencionadas en la definición anterior.
x 1
no es continua en el punto x=1 ya que la función no existe en dicho
x 1
punto pero el límite si existe y tiene un valor de 2(compruébelo).
1) La función: f ( x)
Página
55
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
La función es discontinua evitable en x=1 por existir el límite, sin embargo la función si es continua
en cualquier otro punto de su dominio.
2)
x2
f ( x)
Log ( x)
x 0
x 0
a. f (0) (0)2 0
b. lim f ( x) lim Log ( x)
x 0
x 0
lim f ( x) lim x 2 0
x 0
x 0
lim f ( x) No existe
x 0
c. f (0) lim f ( x)
x 0
La función no es continua en el punto x=0, pero ahora por otra razón al ejemplo anterior: no existe
el límite de la función en dicho punto (no coinciden los límites laterales en cero).
La función es discontinua inevitable en x=0 por no existir el límite.
3)
2
f ( x) 2
x
x 2
x 2
a. f (2) 2
b.
lim f ( x) 4
x 2
c. f (2) lim f ( x)
x 2
La función no es continua en el punto x=2 ya que, si bien existe la función en el punto y existe el
límite, ambas cantidades no coinciden.
La función es discontinua evitable en x=2
3x 5 si x 1
si x 1 , estudiar la continuidad de dicha función en x = 1
4) Dada la función f ( x ) 2
3 x si x 1
Seguiremos el mismo proceso que en los ejemplos anteriores:
a. Estudiamos la existencia del
lim f ( x)
x 1
Como en el punto x = 1 la función experimenta un cambio de definición, para estudiar la existencia
de dicho límite, tendremos que calcular los límites laterales de la función en el punto. Por tanto:
lim
x 1
f ( x) lim (3x 5) 2
x 1
Página
56
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
lim
x 1
f ( x) lim (3 x) 2
En consecuencia, existe
x 1
lim f ( x) 2 pues los límites laterales son iguales.
x 1
b. f (1) 2
c. lim f ( x) f ( 1)
x1
Luego la función es discontinua evitable en el punto x = 1 por existir el límite
Las discontinuidades las podemos resumir de la siguiente forma:
f ( x) f (a) continua
lim
x a
f ( x) existe
lim
x a
lim f ( x) f (a ) discontinua evitable
f (a) está definido
x a
lim f ( x) no existe discontinua no evitable
f ( x)
xa
lim f ( x) existe lim f ( x) f (a ) discontinua evitable
xa
x a
f (a) no definido
lim f ( x) no existe discontinua no evitable
xa
Página
57
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
UNIDAD 3
DERIVADAS Y APLICACIONES
Uno de los grupos temáticos de la Matemática Superior que más se aplica a la Economía es, sin
duda, la derivada. Es utilizada para determinar el producto marginal, elasticidad e importantes
funciones económicas, y para desarrollar los procesos de optimización. Tanto el óptimo
microeconómico del consumidor como del productor, representan un problema de optimización
modelado mediante un proceso en derivadas parciales. Este documento ilustra algunas de las
aplicaciones de la derivada de las funciones de una variable independiente, con énfasis en las
aplicaciones económicas.
CONCEPTOS BÁSICOS
Incrementos y razón (tasa) de cambio
Sea y f ( x) una función definida en el intervalo x1 , x2 , si x cambia de x1 a x 2 entonces el
cambio o variación en x se llama incremento de x: x x2 x1 El correspondiente incremento de
y es y f ( x2 ) f ( x1 )
x x2 x1
y y2 y1 f ( x2 ) f ( x1 )
Dicha variación puede ser positiva o negativa.
El cociente de estos incrementos se llama Razón de cambio promedio o tasa de variación media
de y con respecto a x
f ( x 2 ) f ( x1 )
y
Razón de cambio promedio =
x
x 2 x1
Si las variaciones las medimos para valores de x muy próximos obtendremos la tasa de variación
instantánea o razón de cambio instantánea de y con respecto a x en el punto ( x1 , f ( x1 ) :
f ( x2 ) f ( x1 )
y
Razón de cambio instantáneo = lim
lim
x 0 x
x 0
x2 x1
Ejemplos:
1. Para la función y 4 2 x x 2 , calcular el incremento de x y el incremento de y para
x1 1, x2 2
x x2 x1 2 (1) 3
Página
58
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
2
y1 4 2(1) (1) 4 2 1 7
y y2 y1 4 7 3
2
y
4
2(2)
(2)
4
4
4
4
2
El incremento de y negativo significa una disminución de la función, lo cual quiere decir que al
aumentar la x tres unidades, la función (y) disminuye en tres unidades.
2. El volumen de ventas de gasolina (No. de litros vendidos por día) es q 1,000 200 p , en
donde p es el precio por litro en centavos. Calcular el incremento en el volumen de ventas de
gasolina que corresponde a un incremento en el precio por litro, de $1.50 a $1.60. ¿Cuál es el
incremento en el precio?
p p2 p1 160 150 10 Centavos/litro.
q1 1,000(200 150) 50,000 litros/dia
q q2 q1 40,000 50,000 10,000 Lit / dia
q2 1,000(200 160) 40,000 litros/dia
Lo cual quiere decir que al aumentar el precio por litro en 10 centavos, el volumen de ventas
disminuye en 10,000 litros diarios.
3. Para cierto fabricante, el costo de producción de x toneladas por semana de un producto
químico, expresado en dólares está dado por: C ( x) 50, 000 60 x y el ingreso correspondiente
por la venta de x toneladas semanales de producto químico, expresado también en dólares,
está dado por I ( x) 300 x 0.03x 2 . La compañía actualmente produce 4,000 toneladas por
semana, pero desea incrementar la producción a 4,200 toneladas de producto químico
semanales, calcular:
a) El incremento semanal en los costos de producción.
b) El incremento semanal en los ingresos.
c) El incremento semanal en las utilidades.
d) La tasa de cambio promedio de la utilidad por las toneladas extra producidas.
a. C C (4, 200) C (4, 000) 50, 000 60(4, 200) 50, 000 60(4, 000) 302, 000 290, 000
C $12, 000
b. I I (4, 200) I (4, 000) 300(4, 200) 0.03(4, 200) 2 300(4, 000) 0.03(4, 000)2
I 730,800 720,000 $10,800
c. U I C 10,800 12,000 $ 1, 200
U 1, 200
6 . Lo que significa que, en promedio, por cada tonelada adicional producida y
x
200
vendida por semana, la utilidad disminuye en $6.
Incremento de una función en forma general
x x2 x1 x2 x1 x , como se puede ver en la gráfica.
y y2 y1 f ( x2 ) f ( x1 ) . Por lo tanto sustituyendo x2 se tiene que y f ( x1 x) f ( x1)
para cualquier incremento de x, a partir de un valor conocido de x. En general, para cualquier valor
de x y cualquier incremento de x, se tiene que: y f ( x x) f ( x)
Página
59
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Ejemplo:
f ( x) x 2 4
a) Calcular el incremento de y si x 3, x 0.8
b) Calcular el incremento de y si x 3 , para cualquier incremento de x.
c) Calcular el incremento de y para cualquier valor de x y cualquier incremento de x.
Solución:
a) y f ( x x) f ( x) f (3 0.8) f (3) f (3.8) f (3) (3.8)2 4 (3)2 4 10.44 5 5.44
b) y f ( x x) f ( x) f (3 x) f (3) (3 x) 2 4 (3) 2 4 9 6x (x) 2 4 9 4
y 5 6x (x) 5 6x (x) .
2
2
c)
y f ( x x) f ( x) ( x x)2 4 x 2 4 x 2 2 xx (x)2 4 x 2 4 2 xx (x) 2
La derivada
Definiciones
Línea secante: Es la línea que intercepta la curva en dos o más puntos (Ver figura abajo).
Línea tangente a una curva en un punto P de la misma: Es la línea resultante de la posición límite
de las líneas secantes PQ , siendo Q un punto de la curva acercándose al punto P, ya sea por la
derecha o por la izquierda (Ver figura abajo).
Pendiente de una curva en un punto P de la misma: Es la pendiente, en caso de que exista, de la
línea tangente a la curva en el punto P.
m lim
h 0
f ( x h) f ( x )
h
Otra definición
La pendiente de la recta tangente a la curva y f (x) en el punto P (a, f (a)) es:
m lim
x a
f ( x) f ( a )
xa
Derivada de una función y f ( x) : Es la función denotada por f (x) o por y , definida por:
Página
60
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
y
x 0 x
f ( x) y lím
Siempre que el límite exista.
Geométricamente representa la pendiente de la línea tangente a la curva en cualquier punto de la
misma.
Diferentes formas de representar la derivada de una función y f (x) :
y;
f ( x);
dy
;
dx
df ( x)
;
dx
Dx y ;
Dx f ( x)
La derivabilidad implica la continuidad (aunque no al revés) es decir si f(x) es derivable en un punto
a, entonces es continua en dicho punto.
Esto es equivalente a: “Si f(x) no es continua en un punto a entonces no puede ser derivable en
dicho punto”
Derivadas laterales
Como la derivada de una función es un límite y teniendo presente que, en algunas ocasiones los
límites no existen aunque si sus límites laterales, se pueden dar las siguientes definiciones:
Se llama derivada lateral de f(x) a la izquierda de “a”, al límite, cuando existe y es finito:
.
f (a ) lim
x a
f ( x) f (a )
xa
Se llama derivada lateral de f(x) a la derecha de “a”, al límite, cuando existe y es finito:
f (a ) lim
x a
f ( x) f (a )
xa
Una función es derivable en un punto si existen las derivadas laterales y éstas coinciden.
La derivada como razón de cambio
Definición:
Página
61
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
y
es la razón de cambio promedio de y con respecto a x
x
si y f ( x)
lím y dy es la razón de cambio instantánea de y con respecto a x
x0 x dx
La razón de cambio instantánea se abrevia simplemente como razón de cambio f ( x) y
y representa aproximadamente el cambio de y por cada cambio unitario en x.
Ejemplos
1. Halle la derivada de y x 2 en x = 2
y'
d x2
dx
( x h) 2 x 2
x 2 2 xh h 2 x 2
2 xh h 2
h(2 x h)
lim
lim
lim
h 0
h
0
h
0
h
0
h
h
h
h
lim(2 x h) 2 x
lim
h 0
Entonces :
d x2
dx
2x
En x = 2 la derivada es: 2(2)=4
2. La derivada de y x 3 es
d x3
( x h)3 x 3
x3 3x 2 h 3xh 2 h3 x 3
lim
3x 2
h
0
h
0
dx
h
h
3
d x
Entonces :
3x 2
dx
y'
lim
3. Halle la ecuación de la recta tangente a la gráfica de la función f ( x)
Página
62
x en el punto (4,2)
I I - 2011
dy
,
dx
UNIDADES TECNOLÓGICAS DE SANTANDER
En primer lugar hallemos la pendiente de la recta tangente usando límites:
m lim
h0
xh x
h
lim
h0
( x h x )( x h x )
h( x h x )
( x h) x
h
lim
lim
h0 h( x h x ) h0 h( x h x )
1
1
1
1
lim
h0 ( x h x ) 2 x 2 4 4
Ahora hallemos la ecuación de la recta con la expresión: y m( x x0 ) y0
y
1
4
( x 4) 2
Solución: y
1
4
1
4
x 1 2
1
4
x 1
x 1
Propiedades o reglas de derivación
Sea u f ( x), v g ( x) son funciones cuya derivada existe; c y n son número reales o
constantes.
1. Si y c
4. Si
y 0
2. Si y x
y xn y n x n1
5. Si y cu
y 1
3. Si y cx
y cu
7.
Si y u.v y v.u ' u.v '
10.
Si y eu y ueu
Si y
11.
6.
Si y u v y u v
9.
8.
u
v u - u v
y =
v
v2
Si y u
y
Si y au y au Lnau
y c
Si y ln u y
Si y Log au y
u
u Lna
u
u
u
Ejemplos:
1. y 2 x3 5x 2 7
y 2(3x2 ) 5(2 x) 0 6 x2 10 x . Se aplicaron las reglas 6, 5, 4, 1.
2.
y 3 3 x 3 x1/ 3
3.
g ( x) 5 x
dy
1
1
1
. Se aplicaron las reglas 6, 1, 4.
0 x 2 / 3 2 / 3
3
dx
3
3x
3 x2
3
4
3
4
5 x1/ 2 1/ 2 2 / 3 5 x1/ 2 3x 1/ 2 4 x 2 / 3
3 2
x
x
x
x
5
3
2
1
1
2
g ( x) 5 x 1/ 2 3 x 3 / 2 4 x 5 / 3 1/ 2 3 / 2 5 / 3
2x
3x
2
2
3
2x
Página
63
I I - 2011
u
u
UNIDADES TECNOLÓGICAS DE SANTANDER
g ( x)
5
2 x
3
2 x
3
2
3 x5
3
. Se aplicaron las reglas 6, 5, 4.
3x 2 5
4. Halar la derivada de f ( x)
2x 7
f ( x)
f ( x)
2 x 7Dx 3x 2 5 3x 2 5Dx 2 x 7
2 x 7
2
2 x 76 x 3x 2 5(2) 12 x 2 42 x 6 x 2 10 6 x 2 42 x 10
2 x 72
2 x 72
2 x 72
Se aplicaron las reglas 8, 6, 5, 4,1
1
( x 2 3) ln x(2 x) x 3 2 x ln x
ln x
x
x
5. y 2
.
y
2
2
x 3
( x 3)
( x 2 3) 2
Se aplicaron las reglas 7, 9, 6, 4 y 1.
6. f ( x) e
x5 4 x3
f ( x) e x 4 x 5 x 4 12 x 2 x 2 5 x 2 12 e x 4 x .
5
3
5
3
Se aplicaron las reglas 10, 6, 4, y 5.
Ejemplos aplicados:
0.003 x
1. La ecuación de la demanda para el producto de un fabricante es p 1,000e
.
Evalúa la razón de cambio del precio unitario con respecto al número de unidades, cuando éstas
son 500.
dp
dp
0.003(500)
0.003 x
0.003 x
1.5
1, 000 0.003e
3e
3e
3e
0.6694
dx
dx x500
Es decir, el precio disminuye a razón de $0.6694/unidad por cada unidad adicional demandada.
2. La función de utilidad de una empresa, en miles de pesos, está dada por U ( x) 50 ln( x 1) 90
donde x representa las unidades fabricadas y vendidas. Calcular la razón de cambio de la
utilidad con respecto al número de unidades, cuando se fabrican y venden 10 unidades.
1 50
U ( x) 50
U (10) 4.54545
x 1 x 1
Es decir, la utilidad aumenta $4,545.45 por cada unidad más que se fabrique y venda.
Regla de la cadena
Si f (u) es derivable en u g (x) y g(x) derivable en x, entonces la compuesta ( f g ) ( x ) f ( g ( x))
es derivable en x. Además:
( f g ) '( x ) f '( g ( x)).g '( x)
Usando la notación de Leibniz, si y f (u) , u g ( x) entonces:
Página
64
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
dy
dy du
dx
du dx
Regla de la cadena para potencias
Si u (x) es una función derivable entonces:
d ( un )
du
n u n1
dx
dx
Ejemplos
1. Sea y (3x 2 x 1) 4 halle su derivada
y' 4(3x 2 x 1) 3 (3x 1)
2. Sea y
x 3 x calcule
dy
dx
y x x ( x x)
3
3
1
2
1
dy
1 3
3x 2 1
2
2
( x x) (3x 1)
dx
2
2 x3 x
Derivada de funciones trigonométricas
Derivada de seno de x
d
sen( x) cos( x)
dx
d
sen( x h) sen( x)
sen( x) cos(h) sen(h) cos( x) sen( x)
sen( x) lim
lim
h 0
h 0
dx
h
h
sen( x)(cos(h) 1) sen(h) cos( x)
sen( x)(cos(h) 1
sen(h) cos( x)
lim
lim
lim
h 0
h 0
h 0
h
h
h
cos(h) 1
sen(h)
sen( x) lim
cos( x) lim
sen( x)(0) cos( x)(1) cos( x)
h 0
h 0
h
h
d
sen( x) cos( x)
dx
Derivada de coseno de x
d
cos( x h) cos( x)
cos( x) cos(h) sen(h) sen( x) cos( x)
cos( x) lim
lim
h 0
h 0
dx
h
h
cos( x)(cos(h) 1) sen(h) sen( x)
cos( x)(cos(h) 1
sen(h) sen( x)
lim
lim
lim
h 0
h
0
h
0
h
h
h
cos(h) 1
sen(h)
cos( x) lim
sen( x) lim
cos( x)(0) sen( x)(1) sen( x)
h 0
h
0
h
h
Página
65
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
d
cos( x) sen( x)
dx
Para obtener las demás derivadas no es necesario usar límites ya que empleamos las identidades
que involucran a seno y a coseno.
Derivada de tangente de x
d
d sen( x) cos( x) cos( x) (sen( x)) sen( x) cos 2 ( x) sen 2 ( x)
1
tan( x)
sec2 ( x)
2
2
2
dx
dx cos( x)
(cos( x))
(cos( x))
cos ( x)
d
tan( x) sec2 ( x)
dx
Se puede usar este mismo procedimiento para probar las siguientes derivadas:
d
cot(x) csc 2 ( x)
dx
d
sec( x) sec( x) tan( x)
dx
d
csc( x) csc( x) cot( x)
dx
Derivadas de funciones trigonométricas compuestas
d
du
sen(u ) cos(u )
dx
dx
d
du
4. cot(u ) csc2 (u )
dx
dx
1.
d
du
d
du
cos(u ) sen(u )
3.
tan(u ) sec2 (u )
dx
dx
dx
dx
d
du
d
du
5. sec(u ) sec(u ) tan(u )
6. csc(u ) csc(u ) cot(u )
dx
dx
dx
dx
2.
Ejemplos
1. Derive y sen( x 2 )
y' cos( x 2 )2 x 2 x cos( x 2 )
1 1
2. Derive y sen( )
x 2
1 1
1
1
1 1
y' cos( )( 2 ) 2 cos( )
x 2
x 2
x
x
Derivación implícita
Una función f(x) esta definida implícitamente por una ecuación si y solo si al sustituir y por f(x) se
llega a una identidad.
Ejemplos
2
1. La ecuación y x define dos funciones implícitamente, ellas son:
y f ( x) x , y f ( x) x
Página
66
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
dy
debemos derivar implícitamente la ecuación y 2 x , en primer lugar vamos
dx
Para hallar f ' ( x)
a sustituir y por f(x) en la ecuación, así:
f ( x)2 x , ahora derivamos en ambos miembros con respecto a x y usamos la regla de la cadena
en el miembro izquierdo
1
1
2 f ( x) f '( x) 1
f '( x)
2 f ( x) 2 y
2. Suponga que y 3 7 y x 3 define a y como una función implícita de x, halle
dy
dx
Derivando en ambos miembros:
3 y2.
dy
dy
7 3x 2
dx
dx
dy
(3 y 2 7) 3x 2
dx
dy
3x 2
2
dx 3 y 7
Derivada de una función elevada a otra función
Tambien se conoce como la derivada de la función exponencial compuesta, se puede representar
de la forma:
y UV
Para hallar su derivada podemos podemos usar la formula
Otra forma de derivarla es por medio del logaritmo natural. Se le aplica a los dos lados de la
expresión logaritmo natural (Ln) para por medio de propiedades de logaritmos bajar la función del
exponente y posteriormente derivar cada lado en forma de derivada implicita, para luego despejar
y'
Ejemplo:
Derivar y x x
Ln y Ln x x
1
y ' Lnx 1
y
Ln y x Lnx
1
1
y ' 1. Lnx x
y
x
y ' y Lnx 1
y ' x x Lnx 1
Derivadas de orden superior
Sea y = f(x) una función entonces:
d
f ( x) , es la primera derivada o derivada de primer orden
dx
d2
y '' f '' ( x) 2 f ( x) , es la segunda derivada o derivada de segundo orden
dx
d3
y ''' f '''( x) 3 f ( x) , es la tercera derivada o derivada de tercer orden
dx
y ' f ' ( x)
Página
67
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
.
.y
( n)
f
( n)
( x)
d
n
dx n
f ( x) , es la enésima derivada o derivada de orden n
Ejemplos
1. Halle todas las derivadas de orden superior para y 3x 4 2 x 3 x 2 2
y ' 12 x3 6 x 2 2 x
y '' 36 x 2 12 x 2
vi
yv 0
y 0 .......... y n 0
2. Halle la tercera derivada de y
y ' x2
1
x
y '' 2 x3
y iv 72
y ''' 72 x 12
y ''' 6 x4
Teorema del Valor medio
Si f es una función en la que se cumple que:
1. f es continua en el intervalo cerrado [a, b]
2. f es diferenciable en el intervalo abierto (a, b)
Entonces, existe un número c que pertenece a (a, b) tal que:
f ´(c)
f (b) f (a)
ba
A la izquierda se observa una ilustración de la
interpretación geométrica del Teorema del Valor
medio.
El teorema afirma que si la función es continua
en [a, b] y diferenciable en (a, b), existe un
punto c en la curva, entre A y B, donde la recta
tangente es paralela a la recta que pasa por A y
B. Esto es,
c a, b , tal que f ´(c)
f (b) f (a)
ba
Ejemplo
Para la función cuya ecuación se da, verificar que se cumplen las condiciones del teorema del valor
medio en el intervalo dado, y determinar un valor adecuado "c" que satisfaga la conclusión de este
teorema:
f ( x) x3 x 2 x ; 2,1
Solución:
Por ser f una función polinomial, es derivable para toda x por lo que debe existir por lo menos
Página
68
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
un número c 2,1 , tal que:
f ´(c)
f (1) f (2) 1 2
1
1 2
3
Además f ´( x) 3x 2 2 x 1 por lo que f ´(c) 3c 2 2c 1
1 7
1 7
o c
3
3
1 7 11 5 7
1 7 11 5 7
Luego en
,
y
en
,
la recta tangente es paralela a la
3
27
3
27
recta secante que pasa por los puntos 2, 2 y 1,1
Como f ´(c) 1 entonces 3c 2 2c 1 1 por lo que c
Análisis marginal
Cuando un fabricante tiene una determinada producción de un bien y observa que ésta es menor
que la demanda de su producto, entonces requiere incrementar su producción para satisfacer la
demanda, pero necesita saber si al incrementar dicha producción no se generan gastos excesivos
que disminuyan su ganancia y es así que aparecen los conceptos de costo marginal, ingreso
marginal y beneficio marginal.
a. Costo marginal
Es el costo adicional que se genera al producir una unidad adicional de un producto o servicio.
Tambien se define como la razón de cambio del costo total con respecto al número de artículos
producidos y comercializados (es decir, el costo aproximado de una unidad extra producida).
Si C ( x) es la función del costo total de producción de x artículos
del costo marginal.
El costo total está dado por
dC
C ( x) es la función
dx
C C f CV , es decir la suma de los costos fijos y los costos
variables.
El costo medio unitario de producción de x artículos está dado por: C
C
C Cx
x
Ejemplos:
a. El costo total en dólares de producción de x libras de cierta sustancia química está dado por
C 45 5x2 . Determinar el costo marginal cuando se producen 3 libras de dicha sustancia.
dC
dC
C '
10 x C '
30 , es decir, si la producción se incrementa de 3 a 4
dx
dx x 3
libras, el costo se incrementa 30 dólares.
b. El costo medio unitario en la producción de x unidades es C 0.002 x 2 0.4 x 50
100,000
.
x
Determinar la ecuación del costo marginal y el costo marginal para producir 40 unidades.
C Cx 0.002 x3 0.4 x 2 50 x 100,000 C '
dC
0.006 x 2 0.8 x 50
dx
Página
69
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
dC
dx
9.6 32 50 $27.60 / unidad adicional producida
x 40
b. Ingreso marginal
Es la razón de cambio del valor total recibido con respecto al número de unidades vendidas (Es
decir, el ingreso aproximado recibido por la venta de una unidad adicional vendida).
Si I ( x) es la función del ingreso total por la venta de x unidades
dI
I ( x) es la función
dx
del ingreso marginal.
La función de ingreso se obtiene multiplicando: (precio unitario) ∙ (No. de unidades vendidas), es
decir: I px
Ejemplo: Un fabricante vende un producto a 3x 50 pesos/unidad. Determinar la ecuación del
ingreso marginal y el ingreso marginal para x 100 .
I px 3x 50 x 3x 2 50 x
dI
dI
6 x 50
dx
dx
$650 / unidad adicional vendida
x 100
c. Utilidad marginal
Es la razón de cambio del valor total de la utilidad obtenida con respecto al número de unidades
producidas y vendidas (Es decir, la utilidad aproximada obtenida por la fabricación y venta de una
unidad adicional).
dU
U ( x)
Si U ( x) es la función de la utilidad total por la producción y venta de x unidades
dx
es la función de la utilidad marginal.
La utilidad se calcula restando: (Ingresos) – (Costos), es decir: U I C
Ejemplo: La ecuación de la demanda para el producto de un fabricante es 10 p x 0.01x 2 700 y
2
la función de costo es C ( x) 1, 000 0.01x . Calcular la función utilidad marginal y también evaluar
la utilidad marginal para a) x 100 unidades
b) p $10 /unidad.
Sabemos que la utilidad está dada por U ( x) I ( x) C ( x) y que el ingreso es I px . Por lo tanto
despejamos p de la ecuación de la demanda y lo multiplicamos por x para obtener la función
ingreso:
2
2
2
3
10 p 700 x 0.01x p 70 0.1x 0.001x I ( x) px 70 x 0.1x 0.001x
2
3
2
3
2
U ( x) 70 x 0.1x 0.001x 1, 000 0.01x 0.001x 0.11x 70 x 1, 000
2
U ( x) 0.003x 0.22 x 70 . Esta es la función utilidad marginal, para evaluarla en x = 100
simplemente sustituimos este valor de x en dicha función. Para evaluarla en p = 10 tenemos que
calcular primero cuánto vale x para ese valor de p en la ecuación de la demanda:
2
10(10) x 0.01x 700 . Ordenando la ecuación cuadrática nos queda:
2
0.01x x 600 0 .
Resolviendo la ecuación: x
1 1 4(0.01)(600) 1 1 24 1 25 1 5
4
200
2(0.01)
0.02
0.02
0.02 0.02
Página
70
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
a)
b)
2
U (100) 0.003(100) 0.22(100) 70 30 22 70 = $18/unidad adicional.
2
U (200) 0.003(200) 0.22(200) 70 120 44 70 = $94/unidad extra.
Elasticidad de la demanda
Es el medio por el cual los economistas miden cómo un cambio en el precio de un producto afecta
la cantidad demandada. Se define como:
cambio porcentual en la cantidad demandada cpd
Elasticidad de la demanda =
cambio porcentual en el precio
cpp
Ejemplo: Suponiendo que el precio por artículo se incrementa en un 6% y la cantidad demandada
4
2
0.6667 .
decrece en un 4%, entonces la elasticidad de la demanda es
6
3
De acuerdo con la definición se tiene que:
x
100
px
Elasticidad = x
p
xp
100
p
a. Elasticidad puntual de la demanda ( ).
Se define como:
px
p x p
x p dx px
dx
lím
lím
lím
. En general
0 , por lo tanto
p0 xp p0 x p x p0 p x dp
dp
x
0 . Es decir, como por regla general esta derivada es negativa, ya que al aumentar el precio de
un artículo la demanda baja y viceversa, y como el precio y la demanda son cantidades positivas, la
elasticidad puntual es negativa. Por otra parte de la misma definición de elasticidad se observa que:
cpd
p
p
dx
1
, entonces
cpd cpp . Además tenemos que
dp
dp
cpp
dp xp
x
dx
dx
En resumen:
px
cpd
p
o también
y además cpd cpp o también cpp
x
xp
Ejemplo: Si la ecuación de la demanda es x 300 2 p p 2 , evaluar para p = 15:
a) La elasticidad puntual de la demanda.
b) El cambio porcentual de la demanda si el precio se incrementa en 6%.
c) El cambio porcentual en la demanda si el precio disminuye 4%.
d) El cambio porcentual en el precio si la demanda disminuye 10%
dx
dx
2 2(15) 28
2 2 p . Si p 15 x 300 2(15) (15) 2 105 y
dp
dp
px 15(28)
4
a)
x
105
Página
71
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
b) cpd (cpp) 4 (6) 24 , es decir la demanda disminuye en 24%.
c) cpd (cpp) 4 (4) 16 , es decir la demanda aumenta en 16%.
d) cpp
cpd
10
4
2.5 , es decir el precio aumentó 2.5%
b. Tipos o categorías de elasticidad
1.
Si 1 , es decir 1
2.
Si 1 0 , es decir 1
3.
Si 1 , es decir 1 la demanda tiene elasticidad unitaria.
la demanda es elástica.
la demanda es inelástica.
Ejemplo
p 1,875 x 2
dp
dx
2 x
p
xp
Si x 20
p 1,875 (20)2 1, 475
Si x 25
p 1,875 (25) 2 1, 250
Si x 30
p 1,875 (30)2 975
p
x 2 x
p
2 x 2
1, 475
1.84 . Por lo tanto es elástica.
2(20)2
1, 250
1 . Por lo tanto es unitaria.
2(25)2
975
0.54 . Por lo tanto es inelástica.
2(30)2
Se puede calcular para los tres casos, el cambio porcentual en la demanda cuando el precio baja
por ejemplo 3%. Como cpd cpp , para cpp 3 cpd 1.84 3 5.52 , es decir que:
Cuando x = 20, si el precio disminuye en 3%, la demanda se incrementa en 5.52%,
Cuando x = 25, si el precio disminuye en 3%, la demanda se incrementa también en 3%
Cuando x = 30, si el precio disminuye en 3%, la demanda se incrementa en 1.62%.
En general:
Cuando la demanda es elástica, un cambio porcentual en el precio provoca un cambio
porcentual mayor en la cantidad demanda.
Cuando la demanda tiene elasticidad unitaria, un cambio porcentual en el precio provoca un
cambio porcentual igual en la cantidad demandada.
Cuando la demanda es inelástica, un cambio porcentual en el precio provoca un cambio
porcentual menor en la cantidad demandada
Ejemplos:
1. La ecuación de la demanda para el producto de un fabricante es
p
600
. Evaluar la
3x 2
elasticidad puntual de la demanda y su tipo cuando la producción y venta es de 50 unidades.
Página
72
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
3x 2 (0) 600(3) 1,800 . p
2
2
xp
dx
3x 2
3x 2
600
3x 2
dp
Si x 50
3(50) 2
3(50)
152
150
76
75
1,800
x
3 x 2 2
600 3 x 2
2
1,800 x 3 x 2
3x 2
3 x
.
1.0133 . Por lo tanto es elástica.
Otra forma:
Si x 50 p
600
3(50) 2
3.947368421
50(0.077908587)
600
152
3.947368421 ;
dp
dx
1800
3(50) 2
2
1,800
23,104
0.077908587
1.0133 .
2. La ecuación de la demanda para el producto de un fabricante es x p 2 30 p 300 , x 0.
Evaluar la elasticidad puntual de la demanda y su tipo, cuando el precio de venta del artículo es
$10. Evaluar también el cambio porcentual en la demanda si el precio disminuye 4%.
dx
dx
2 p 30 . Si p 10 x (10)2 30(10) 300 100 y
2(10) 30 10
dp
dp
px 10(10) 100
1 . Por lo tanto tiene elasticidad unitaria.
x
100
100
cpd (cpp) (1)(4) 4% , es decir, si el precio disminuye 4%, la demanda aumenta 4%.
x
3. La ecuación de la demanda para el producto de un fabricante es p 200e 100 . Evaluar la
elasticidad puntual de la demanda y su tipo, cuando la producción y venta es de 100 unidades.
x
x
x
dp
p
200e 100
200
100
1
100 ;
200e 100
.
2e
x
dx
xp
x( 2) x
100
x 2e 100
Si x 100
Otra forma:
100
1 . Luego tiene elasticidad unitaria.
100
1
p 200e
Si x 100
p 2e
1
;
200e1
200
1
200
100 2e1
4. La ecuación de la demanda para el producto de un fabricante es x 600 100ln p . Evaluar la
elasticidad puntual de la demanda y su tipo, cuando el precio de venta del artículo es $54.59.
Evaluar también el cambio porcentual en el precio si la demanda disminuyó 5.5%.
Página
73
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
dx
dp
1 100
p .
p
100
px
x 600 100 ln 54.59 200
Si p 54.59
100
x
1.8318
54.59
54.59(1.8318)
0.49998981 . Por lo tanto es inelástica.
x
200
cpd 5.5
cpp
11 , es decir el precio aumentó aproximadamente 11%.
0.5
c. Relación entre la elasticidad y el ingreso
Si la demanda es elástica, al disminuir el precio del producto, la demanda de éste aumenta en
un porcentaje mayor, por lo que el ingreso es mayor. Es decir, un menor precio hace crecer la
demanda en forma suficiente para que el ingreso aumente, a pesar de haber bajado el precio
del producto. También se concluye que al aumentar el precio del producto, la demanda baja en
un porcentaje mayor, por lo cual el ingreso disminuye.
Si la demanda es inelástica, al disminuir el precio del producto la demanda aumenta en un
porcentaje menor, por lo que a pesar de que se venden más unidades el ingreso es menor. Es
decir, al disminuir el precio la demanda aumenta, pero no lo suficiente para compensar la
disminución del ingreso, por la baja del precio del producto. También se concluye que al
aumentar el precio del producto, la demanda baja en una proporción menor, de tal forma que el
ingreso aumenta
Si la demanda tiene elasticidad unitaria, al disminuir el precio del producto la demanda
aumenta en el mismo porcentaje, de tal manera que el ingreso ni aumenta ni disminuye. Es
decir, un menor precio hace crecer la demanda en forma tal que el ingreso permanece sin
cambio. También un mayor precio hace decrecer la demanda en forma tal que el ingreso no
cambia
Ejemplo:
La ecuación de la demanda para el producto de un fabricante es p
3, 500
400 3 x 2
. Contestar las
siguientes preguntas para una demanda de 10 unidades:
a) ¿Cuál es el precio unitario del artículo?
b) ¿Cuál es la elasticidad puntual de la demanda y su tipo?
c) ¿Cuál es el número aproximado de unidades en las que se incrementa la demanda al disminuir
el precio un 12%?
d) ¿El ingreso para el fabricante: aumentará, disminuirá o permanecerá constante, al disminuir el
precio del artículo en un 12%? ¿Por qué?
Solución
a)
b)
p
3, 500
3, 500
3, 500
$5/unidad.
2
700
400 3(10) 400 300
400 3x 2 0 3, 500 6 x
21, 000 x
2
2
dx
400 3x2
400 3x2
dp
Página
74
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
2
400 3(10) 2
dx 400 3 x
2
dp
21, 000 x
x10
21, 000(10)
px
x
2
700
2
210, 000
490, 000
210, 000
49
21
7
3
5 7 7
1.1667 . Por lo tanto es elástica.
10 3 6
x
x(cpd ) 10(14) 14
7
(12) 14% , y como cpd x (100) x 100 100 10 1.4
6
Es decir, la demanda se incrementa 1.4 unidades.
e) El ingreso aumentará, porque la demanda es elástica, de tal manera que al bajar el precio 12%,
la demanda aumenta en un porcentaje mayor (14%).
Comprobación: I1 p1x1 (5)(10) $50.00
c)
cpd cpp
I 2 p2 x2 (4.40)(11.4) $50.16
Razones de cambio relacionadas
¿Cuán rápido varía una cantidad? En general, una razón de cambio con respecto al tiempo es la
respuesta a esta pregunta. La derivada
dy
de una función y=f(x) es una razón de cambio
dx
instantánea con respecto a la variable x. Si la función representa posición o distancia entonces la
razón de cambio con respecto al tiempo se interpreta como velocidad.
Si dos cantidades están relacionadas entre sí, entonces cuando una de ellas cambia con el tiempo,
la otra cambiará también. Por lo tanto sus razones de cambio (con respecto al tiempo) están
relacionadas entre sí. Por ello a este tipo de situaciones se les llama razones de cambio
relacionadas.
Los problemas de razones de cambio relacionadas se resuelven siguiendo los siguientes pasos:
1.
2.
3.
4.
5.
Hacer una ilustración de la situación planteada.
Identificar con símbolos las cantidades que varían en el tiempo.
Identificar las razones que se conocen y la razón que se busca.
Escribir una ecuación que relacione las variables.
Derivar implícitamente con respecto al tiempo la ecuación obtenida en el paso 4.
Ejemplo 1
Un recipiente cónico (con el vértice hacia abajo) tiene 3 metros de ancho arriba y 3,5 metros de
hondo. Si el agua fluye hacia el recipiente a razón de 3 metros cúbicos por minuto, encuentre la
razón de cambio de la altura del agua cuando tal altura es de 2 metros.
Solución. Sea
el volumen del recipiente,
el nivel del agua en el instante .
el radio de la superficie variable en el instante
Página
75
I I - 2011
y
UNIDADES TECNOLÓGICAS DE SANTANDER
dV
3 m3 min .
dt
Dato: Rapidez con que aumenta el volumen del agua; o sea
Encontrar: Rapidez con que sube el nivel del agua cuando la profundidad es de 2 metros; es decir,
dh
dt h2 m
La ecuación que relaciona las variables es el volumen del cono: V
3
r2 h
(1)
Ahora bien, como el volumen consta de dos variables ( y ), conviene, en este caso, expresarlo
únicamente en términos de la altura , para lo cual se usará la relación que existe entre las
variables citadas, a saber, por semejanza de triángulos:
r
h
1.5 3.5
Sustituyendo en (1) se tiene que: V
r
→
3
3
h
7
.
2
h h
37
V
3 3
h
49
La ecuación de razones relacionadas se obtiene derivando implícitamente, respecto del tiempo, a
ambos lados de la ecuación V
3 3
h , lo cual nos conduce a:
49
dV 9 2 dh
h
(2)
dt
49 dt
Finalmente, como se desea encontrar la variación de la profundidad del agua en el instante en que
dV
3 , sustituimos estos valores en (2) para obtener:
dt
9
dh 3 49
49
dh
2 dh
3
1.2998
2
49
dt
dt 4 9
12
dt
Por lo tanto, el nivel del agua aumenta a una razón aproximada de 1.3 m min .
h 2 y dado que
Ejemplo 2
Página
76
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Una empresa tiene la función de costo C ( x) 30 4 x
1 2
x , en donde x es el nivel de
20
producción. Si éste es igual a 5 actualmente y está creciendo a una tasa de 0.5 por año. Calcule la
tasa en que los costos de producción se están elevando.
Solucion:
dx
0.5 (cuando el tiempo se mide en años)
dt
dC
1
4 x
El costo marginal está dado por,
dx
10
Sabemos que
Por consiguiente,
dC dC dx
x dx
4
dt
dx dt 10 dt
Sustituyendo x=5, el nivel de producción actual, obtenemos
dC
5
4 0.5 1.75
dt
10
Asi que los costos de producción se están incrementando a una tasa de 1.75 por año.
APLICACIONES DE LA DERIVADA
El problema de recta tangente
Dada una función f(x), se trata de definir la tangente a la curva en un punto P.
Como ya se vio en la interpretación geométrica de la derivada, la derivada de una función en un
punto x 1 y1 expresa la pendiente de la recta tangente a la función en ese punto.
m f '( x) y '
Por tanto, la ecuación (punto-pendiente) de la recta tangente a la curva en el punto P a, f (a) es:
y f (a) f '(a) x a
y y 1 m x x1
La primera derivada y la gráfica de una función
Utilizaremos el criterio de la primera derivada para analizar dónde una función es creciente o
decreciente, calcular sus valores críticos, localizar sus valores máximos y mínimos relativos y
esbozar su gráfica.
1. Funciones creciente o decreciente
Definición: Sean x1 y x 2 dos números reales cualesquiera de un intervalo I, siendo x1 x2 . Se
dice que:
f ( x) es creciente en el intervalo I si y sólo si f ( x1 ) f ( x2 )
f ( x) es decreciente en el intevalo I si y sólo si f ( x1 ) f ( x2 )
Página
77
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Gráfica 1
En la gráfica 1 se puede ver que la función es creciente en (, 2) y (4, ) , y es decreciente en
(2, 4) .
Criterios para determinar si una función es creciente o decreciente:
Si f ( x)es derivable en el intervalo I ( a, b)
f ( x) 0 para toda x en el intervalo I, entonces f ( x) es creciente en dicho intervalo
y si
f ( x) 0 para toda x en el intervalo I, entonces f ( x) es decreciente en dicho intervalo
Ejemplo: Determinar para qué valores de x la función y x 2 4 x 3 es creciente o decreciente.
f ( x) x² 4 x 3 . Derivando la función se obtiene:
f ( x) 2 x 4 2( x 2) . Analizando la derivada, se tiene que:
Si x 2, entonces f ( x) 0, por lo tanto f ( x) es decreciente .
Si x 2, entonces f ( x) 0, por lo tanto f ( x) es creciente .
Gráfica 2
En la gráfica 2 se pueden comprobar estos resultados.
Valores críticos
Son los valores de x, dentro del dominio de la función, en donde la derivada es cero o en donde la
derivada no existe (es decir, no está definida).
Haciendo referencia a la gráfica 1, x 2, x 4, x 6 son valores críticos, porque en el primero
y en el tercero la derivada es cero, ya que la tangente es horizontal, y en el segundo la derivada no
existe, ya que existen dos tangentes para un mismo punto. Haciendo referencia a la gráfica 2,
existe un solo valor crítico: x 2 (ahí la derivada es cero).
El punto correspondiente a un valor crítico, en la gráfica de una función, se llama punto crítico. En
la gráfica 2 el punto P(2, 1) es un punto crítico.
Página
78
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
2. Extremos de una función
Una función puede tener más de un punto de máximo y/o de mínimo. (Véase la figura 3).
Figura 3
Figura 4
Los valores extremos pueden ser interiores o extremos del intervalo.
En la figura 4, c y d no son máximo y mínimo, respectivamente, en [a, b], pero sí en una
vecindad.
Extremos locales de una función
Son los valores máximos o mínimos locales de una función dentro de su dominio.
Definición: Si I es un intervalo abierto (generalmente muy pequeño) que contiene al valor x 0 .
Se dice que:
f ( x0 ) es máximo local o relativo de f ( x), si y sólo si f ( x0 ) f ( x) para toda x del intervalo
f ( x0 ) es mínimo local o relativo de f ( x), si y sólo si f ( x0 ) f ( x) para toda x del intervalo
Haciendo referencia a la gráfica 1, f (2) 3 es máximo relativo, f (4) 1 es mínimo relativo y
f (6) 3 no es ni máximo ni mínimo relativo.
Criterios para determinar los extremos relativos (locales) de una función
a. Criterio de la primera derivada
Sea f(x) continua en un intervalo abierto que contenga al valor crítico x 0 .
1. Si la función tiene extremos relativos, necesariamente ocurren en los valores críticos. Haciendo
referencia a la gráfica 1, existen extremos relativos en x 2 y en x 4 , que son valores críticos
de la función.
2. Si la derivada de la función cambia de signo al pasar por un valor crítico, necesariamente ahí
existe un extremo relativo; si no lo hace, no tiene extremo relativo en ese valor crítico. Haciendo
referencia a la gráfica 1, no existe extremo relativo en x 6 . Por tanto, no necesariamente en
todos los valores críticos de la función existen extremos relativos.
Página
79
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
3. Si por la izquierda de un valor crítico x 0 , la derivada es positiva (es decir, la función es
creciente) y por la derecha la derivada es negativa (es decir, la función es decreciente),
entonces f ( x0 ) es un máximo relativo de la función.
Si por la izquierda de un valor crítico x 0 , la derivada es negativa (es decir, la función es
decreciente) y por la derecha la derivada es positiva (es decir, la función es creciente), entonces
f ( x0 ) es un mínimo relativo de la función.
Haciendo referencia a la gráfica 1, esto se puede constatar.
Con esta información que nos proporciona la primera derivada de una función, se puede hacer un
esbozo de la gráfica de la función.
Ejemplos
Hacer un análisis mediante la primera derivada, para bosquejar las gráficas de las siguientes
funciones:
1. y 2 x3 3x 2 36 x 5 . Primero calculamos los valores críticos de la función, por lo cual la
derivamos y la factorizamos:
y 6 x2 6 x 36 6( x 2 x 6) 6( x 3)( x 2)
Se observa que la derivada es cero en x 2 y en x 3 , por lo tanto son valores críticos. Ahora
los analizaremos por la izquierda y por la derecha, para ver si la derivada es positiva o negativa y
así concluir si la función es creciente o decreciente:
Si x 2, entonces f ( x) 6()() 0, por lo tanto la función f ( x) es creciente .
Si 2 x 3, entonces f ( x) 6()() 0, por lo tanto la función f ( x) es decreciente .
Si x 3, entonces f ( x) 6()() 0, por lo tanto la función f ( x) es nuevamente creciente .
Esto se puede visualizar mejor si construimos la siguiente tabla:
Intervalo
3,
, 2
2,3
Derivada
Función
+
Creciente
–
Decreciente
+
Creciente
Existe un máximo local o relativo en x 2
Existe un mínimo local o relativo en x 3
Si sustituimos estos valores de x en la función original obtenemos respectivamente los valores
máximo y mínimo relativos de la función, que son: y 49 y y 76 . Por lo tanto podemos expresar
ahora los puntos máximo y mínimo relativos o locales de la función:
Punto máximo P(2,49) .
Punto mínimo P(3, 76)
Situando estos puntos en el sistema de coordenadas cartesianas en dos dimensiones, se puede
construir la gráfica de la función. Esta se muestra en la (gráfica No. 3), donde se comprueban los
resultados del análisis de la función a través de su primera derivada.
Página
80
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Gráfica No. 3: y 2 x3 3x 2 36 x 5
2 3
2
2. f ( x) x 6 x 54 x 120
3
Seguiremos el mismo procedimiento que en el ejemplo anterior:
2
2
f ( x) 2 x 12 x 54 2( x 6 x 27) 2( x 9)( x 3)
La derivada es cero en x 9 y en x 3 , por lo tanto son valores críticos. Ahora construiremos
una tabla similar a la anterior:
–2(–)(–) = –
–2(–)(+) = +
Intervalo
, 9
9,3
Derivada
Función
–
Decreciente
+
Creciente
–2(+)(+) = –
3,
–
Decreciente
Existe un mínimo local o relativo en
Existe un máximo local o relativo en
x 9
x3
Los valores mínimo y máximo relativos de la función, que son: y 366 y y 210 . Por lo tanto los
puntos mínimo y máximo relativos o locales de la función son:
Punto mínimo Pm (9, 366) .
Punto máximo PM (3, 210)
La gráfica de la función se muestra en la (gráfica No. 4), donde se comprueban los resultados de
este análisis
2 3
2
Gráfica No. 4: f ( x) x 6 x 54 x 120
3
Página
81
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
3.
3
f ( x) x 2 3 .
f ( x) 3 x 2 . Existe un solo valor crítico: x 2
2
Intervalo
3()2
, 2
Derivada
Función
+
Creciente
3()2
2,
+
Creciente
No existen ni mínimo ni máximo local o relativo en el punto crítico
P(2,3) .
La gráfica 5 muestra estos resultados.
3
f ( x) x 2 3
Gráfica No. 5:
4. Problema de aplicación:
Para el producto de un
fabricante
la
función
ingreso
en
pesos,
está
dada
por
I ( x) 240 x 57 x x , para 0 x 60 , donde x son las unidades que se venden. Calcular el nivel
de ventas para obtener un ingreso máximo.
2
3
I '( x) 240 114 x 3x² 3( x² 38 x 80) 3 x 40 x 2 .
Valores críticos x 2 y x 40 .
El valor negativo no tiene sentido en el problema, ya que el dominio de la función es 0 x 60 .
–3(–)(+) = +
Intervalo
Ingreso marginal
Ingreso
0, 40
–3(+)(+) = –
40, 60
+
–
Creciente
Decreciente
Se concluye que:
Existe máximo en x 40
El valor máximo es I 36,800
El punto máximo es PM 40, 36800
Por lo tanto para que el ingreso sea máximo, el nivel de producción debe ser de 40 unidades. El
ingreso máximo es de $36,800, que está representado en la gráfica 6, a continuación, por el punto
PM (40 unidades,$36800) .
Página
82
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Gráfica No. 6:
2
I ( x) 240 x 57 x x
3
b. Criterio de la segunda derivada
Si f ( x) es una función que tiene un valor crítico en x a , tal que f (a) 0 y f (a) existe ,
Entonces:
f (a) 0 f ( x) tiene un máximo local o relativo en x a
Si f (a) 0 f ( x) tiene un mínimo local o relativo en x a
f (a) 0 no se puede concluir si f ( x) tiene má ximo o mínimo local en x a
Ejemplo 1:
Aplicar el criterio de la segunda derivada para verificar si la función f ( x) 2 x3 3x 2 36 x 7 tiene
valores máximos o mínimos relativos.
Solución
Primero localizamos sus valores críticos, es decir los valores de x donde la derivada es cero o
donde la derivada no existe:
f ( x) 6 x2 6 x 36 6( x2 x 6) 6 x 3 x 2 . Vemos que la derivada existe para todo valor
de x, y que existen dos valores de x donde la derivada se hace cero. Por tanto sus valores críticos
son: x 2 y x 3
Como f (2) 0 y f (3) 0 , probamos ahora el signo de la segunda derivada para estos valores:
f ( x) 12 x 6
f (2) 12(2) 6 30 . Como es negativa existe un máximo relativo o local en x 2
f (3) 12(3) 6 30 . Como es positiva existe un mínimo relativo o local en x 3
El valor máximo local de la función es f (2) 2(2)3 3(2) 2 36(2) 7 51
El valor mínimo local de la función es f (3) 2(3)3 3(3)2 36(3) 7 74
Pmín (3, 74)
Los puntos máximo y mínimo relativos son: Pmáx (2,51);
Su representación gráfica se puede ver en la siguiente página:
Página
83
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Gráfica de la función f ( x) 2 x3 3x 2 36 x 7
Ejemplo 2:
Aplicar el criterio de la segunda derivada para verificar si la función f ( x) x 4 4 tiene valores
máximos o mínimos relativos.
Solución
f ( x) 4 x3 . Como se puede observar, la derivada existe para todo valor de x, y es cero cuando x
toma el valor de cero. Por lo tanto tiene un sólo valor crítico x 0 . Veamos ahora cómo es el signo
de la segunda derivada en este valor crítico.
f ( x) 12 x 2 .
Como f (0) 12(0)2 0 , entonces no se puede concluir si existe o no máximo o mínimo relativo en
x 0 Así pues, para saber si existe o no máximo o mínimo local tenemos que utilizar el criterio de la
primera derivada:
I
(, 0)
(0, )
f ( x)
-
+
La función es decreciente en el intervalo (, 0) y creciente en el
intervalo (0, ) , luego existe un mínimo relativo o local en
2
f ( x) Decreciente
Creciente El valor mínimo es f (0) (0) 4 4 .
El punto mínimo es P(0, 4) .
Su representación gráfica se puede ver en la siguiente gráfica:
Página
84
I I - 2011
x0
UNIDADES TECNOLÓGICAS DE SANTANDER
Gráfica de la función f ( x) x 4 4
Ejemplo 3
Aplicar el criterio de la segunda derivada para verificar si la función f ( x) 2 x3 tiene valores
máximos o mínimos relativos.
Solución
f ( x) 3x 2 . Como se puede observar, la derivada existe para todo valor de x, y es cero cuando x
toma el valor de cero. Por lo tanto tiene un sólo valor crítico en x 0 . Veamos ahora cómo es el
signo de la segunda derivada en este valor crítico.
f ( x) 6 x .
Como f (0) 6(0) 0 , entonces no se puede concluir si existe o no máximo o mínimo relativo en
x 0 . Así pues, para saber si existe o no máximo o mínimo local tenemos que utilizar el criterio de
la primera derivada:
I
(, 0)
(0, )
f ( x)
-
-
f ( x)
Decreciente
Decreciente
La función es decreciente en los dos intervalos, por lo tanto se
concluye que la función no tiene ni máximo ni mínimo relativo o local
en todo su dominio. El punto crítico es P (0, 2) .
Su representación gráfica se puede ver a continuación.
Gráfica de la función
f ( x) 2 x 3
Extremos absolutos de una función
Extremos absolutos: Son los valores más grande y más pequeño de una función en un intervalo
dado, si es que existen.
Definición: Sea I un intervalo cualesquiera que contenga a x0 . Se dice que:
f ( x0 ) es máximo absoluto de f ( x) en el intervalo I
intervalo.
Página
85
s i y s ó l fo x0s i f ( x para
)
(toda
) x del
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
f ( x0 ) es mínimo absoluto de f ( x) en el intervalo I si y sólo si f ( x0 ) f ( x) para toda x del intervalo.
a
Gráfica 1
a
b
c
Gráfica 2
a b
Gráfica 3
c
Gráfica 4
En la gráfica 1, f (a) es mínimo absoluto de f ( x) en el intervalo , . No tiene máximo
absoluto porque la función viene del infinito y se va al infinito.
En la gráfica 2, f (b) es máximo absoluto de f ( x) en el intervalo a, c . No tiene mínimo
absoluto porque no está definida la función en a y en c. Es decir cada vez que x está más cerca
de a por su derecha, la función está más cerca de f (a) , pero nunca llega a tomar ese valor. Lo
mismo sucede cuando x está cada vez más cerca c por su izquierda.
En la gráfica 3, f (b) es mínimo absoluto y f (c) es máximo absoluto de f ( x) en a, c .
En la gráfica 4, la función no tiene ni máximo ni mínimo absolutos porque viene del menos
infinito, se va al infinito, regresa del menos infinito y finalmente se va al infinito.
Teorema del valor extremo: Si una función es continua en un intervalo cerrado, entonces la
función tiene necesariamente un valor máximo y un valor mínimo absolutos en ese intervalo.
a b
c
Gráfica 1
d
a
b
c
Gráfica 2
d
a
b
c
Gráfica 3
d
En la gráfica 1 f (c) es mínimo absoluto y f (d ) es máximo absoluto de f ( x) en el intervalo a, d .
En la gráfica 2 f (b) es mínimo absoluto y f (c) es máximo absoluto de f ( x) en el intervalo a, d .
En la gráfica 3 f (a) es mínimo absoluto y f (d ) es máximo absoluto de f ( x) en el intervalo a, d .
Se puede observar que los extremos absolutos en un intervalo cerrado ocurren o en los
valores críticos de la función en ese intervalo o en los extremos de dicho intervalo.
Pasos a seguir para determinar los extremos absolutos de una función en un intervalo cerrado:
Sea f(x) continua en un intervalo cerrado a, b .
1. Se obtienen los valores críticos de la función.
Página
86
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
2.
3.
Se evalúa la función en los valores críticos que pertenecen al intervalo cerrado y también en los
extremos del intervalo.
Se seleccionan, de entre estos valores, el valor más grande y el valor más pequeño de la
función, los cuales serán respectivamente el máximo absoluto y el mínimo absoluto de esta en
el intervalo cerrado dado.
Ejemplos
Determinar los extremos absolutos de la función en los intervalos dados:
1.
f ( x) x 2 2 x 3; 1,3
f ( x) 2 x 2 2( x 1) . Valor crítico x 1 , el cual pertenece al intervalo dado.
f (1) (1)2 2(1) 3 6;
f (1) (1)2 2(1) 3 2;
f (3) (3) 2 2(3) 3 6 .
Por lo tanto el valor máximo absoluto de la función en el intervalo dado es 6 y el valor mínimo
absoluto de la función en ese intervalo es 2.
2.
f ( x) 2 x2/ 3 ; 1,8,
1,8 .
La función se puede representar como f ( x) 2 3 x 2 , la cual existe y es continua para toda x
real.
4
4
f ( x) x 1/ 3 3 . Valor crítico x 0 . Este valor crítico no se encuentra en el intervalo 1,8 ,
3
3 x
pero sí en el intervalo 1,8 . Por lo tanto:
Para el intervalo 1,8 , evaluamos la función sólo en los extremos del intervalo:
f (1) 2 3 (1)2 2;
f (8) 2 3 (8)2 8
Así que 2 es el mínimo absoluto y 8 es el máximo absoluto de la función en ese intervalo.
f (0) 2 3 0 0;
f (8) 2 3 (8)2 8
Para el intervalo 1,8 , f (1) 2 3 (1)2 2;
Así que 0 es el mínimo absoluto y 8 es el máximo absoluto de la función para este intervalo.
3.
f ( x)
f ( x)
5x
; 3,4 .
x2 4
x2 4 (5) 5x(2 x)
x
2
4
2
5 x 2 20 10 x 2
x
2
4
2
20 5 x 2
x
2
4
2
5 4 x2
x
2
4
2
5 2 x 2 x
x
2
4
2
.
Valores críticos x 2; x 2 , ambos pertenecen al intervalo dado. Por lo tanto evaluamos:
15
10
5
10 5
20
f (3)
;
f (2)
;
f (2) ;
f (4)
1
13
8
2
8 2
20
Así que -5/2 es el mínimo absoluto y 5/2 es el máximo absoluto de la función ese intervalo.
Relación de los extremos absolutos con los extremos relativos de una función
Si una función tiene sólo un extremo relativo en un intervalo dado, entonces también es extremo
absoluto en ese intervalo. Es decir, si f (a) es un mínimo relativo de la función en un intervalo, y es
único (no hay máximo relativo), entonces f (a) es mínimo absoluto en el intervalo. Si f (a) es un
Página
87
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
máximo relativo de la función en un intervalo, y es único (no hay mínimo relativo), entonces f (a) es
máximo absoluto.
Ejemplo
Cierta compañía ofrece un seminario sobre técnicas de administración. Si la cuota es de 600
dólares por persona, asisten al seminario 1,000 personas. Pero por cada disminución de 20 dólares
en la cuota, asisten 100 personas más. Sin embargo, debido a recursos limitados, es posible recibir
a lo más 2,500 personas. Calcular cuál es el número de personas que proporcionarían un ingreso
máximo a la compañía, cuál sería el ingreso máximo y cuál sería la cuota que se cobraría a las
personas por asistir al seminario.
Solución:
Sea n el número de disminuciones de $20 en la cuota de asistencia al seminario. Entonces la cuota
por persona y el número de personas que asistirán serán:
Cuota por persona: p = 600 – 20n
Número de personas: x = 1,000 + 100n
El máximo número de personas es 2,500. Por lo tanto 1,000 100n 2500 n 15 . Es decir, el
número de disminuciones de $20 en la cuota, no debe de exceder de 15.
Ingreso = (cuota por persona)(número de personas). Es decir I = px.
I (n) (600 20n)(1,000 100n) 600,000 60,000n 20,000n 2,000n2 . Por tanto la función ingreso es
I (n) 600,000 40,000n 2,000n2 ; para 0 n 15 , es decir en el intervalo 0,15 .
I (n) 40,000 4,000n 4,000(10 n) . Existe un sólo valor crítico n 10
I
I (n)
I ( n)
0,10
10,15
+
-
Creciente
Decreciente
El ingreso es creciente en el intervalo
el intervalo
0,10 y decreciente en
10,15 , por lo tanto existe un máximo relativo para
el ingreso cuando
n 10 .
Como el extremo relativo es único, es también máximo absoluto. Por lo tanto para ingreso máximo
se debe disminuir en $20 la cuota por persona 10 veces, es decir (10)(20) = $200.
El número de personas que asistirían al seminario es 1,000 + 100(10) = 2,000 personas.
El ingreso máximo sería I (10) 600,000 40,000(10) 2,000(10) 2 $800,000 .
La cuota por persona sería de 600 – 20(10) = $400.
3.
Concavidad de una función
En las figuras 1 y 2, observe que cada curva y f (x) se “flexiona” (o abre) hacia arriba.
y
y
0
0
x
x
Figura 1
Figura 2
Si se trazan tangentes a las curvas, las curvas quedarán “por arriba” de estas. Además, las
pendientes de las líneas tangentes crecen en valor al crecer x. Luego, f es una función creciente.
Página
88
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Se dice entonces que la función es cóncava hacia arriba(o convexa).
Si la curvas se encuentran “por debajo” de las tangentes, se flexionan hacia abajo. (Véanse los
gráficos de las figuras 3 y 4).
y
0
x
Figura 3
Figura 4
Cuando x crece, las pendientes decrecen, luego, f es una función decreciente. Decimos que f
es cóncava hacia abajo(o cóncava).
Criterio de concavidad
Sea f derivable en (a, b).
Si f (x) > 0 para toda x (a, b), entonces f es cóncava hacia arriba en (a, b).
Si f (x) < 0 para toda x (a, b), entonces f es cóncava abajo en (a, b).
Ejemplo
Analizar la concavidad de la función f (x) = x 3 .
Solución:
a) f (x) = x 3 f (x) 3x 2 f (x) 6x
f (x) < 0 para x < 0 y f (x) > 0 para x > 0. Luego, si x < 0, f es cóncava hacia abajo; si x > 0,
f es cóncava hacia arriba. Compruebe este resultado en la gráfica de la figura 5.
Figura 5
Punto de inflexión
Definición
Una función tiene un punto de inflexión en x = x0 si y solo si, f es continua en x0 y f cambia de
concavidad en x0.
Página
89
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Entonces, x0 es un posible punto de inflexión si:
1. f ( x0 ) 0 ; o no existe f ( x0 ) , pero sí f ( x0 ) .
2. f debe ser continua en ese punto.
Ejemplo
Analizar la concavidad y encontrar los puntos de inflexión de f (x) = 6 x 4 8x 3 1 .
Solución:
f (x) 24 x 3 24 x 2 24( x 3 x 2 ) f (x) 24 (3x 2 2 x) = 24x (3x -2)
Luego, f ( x) 0 en x = 0, y en x =
2
, que son posibles puntos de inflexión.
3
Se procede de forma análoga a la solución de una inecuación, como lo hemos visto anteriormente.
Ubiquemos los signos en un rayo numérico para observar los cambios de signo de la segunda
derivada. (Figura 1).
En (- ; 0) f es cóncava hacia arriba, al igual que en (
pues en estos intervalos f es positiva.
Figura 1
En (0;
2
; + ),
3
2
) f es cóncava hacia abajo, pues f es negativa.
3
2
son puntos de inflexión, pues hay cambio de signo de la segunda derivada
3
alrededor de estos puntos. Recuerda que son puntos de inflexión, si f es continua en esos puntos
Luego, x = 0 y x =
y existe cambio de signo de la segunda derivada alrededor de estos ellos. Verifique este resultado
en la figura 6.
Figura 6
Representación gráfica de funciones
Los puntos de análisis previos a la representación gráfica de una función son:
Dominio
Continuidad
Puntos de corte con los ejes coordenados.
Simetrías
Asíntotas
Crecimiento y decrecimiento
Extremos(máximos y mínimos)
Página
90
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Curvatura y puntos de inflexión
Tabla de resumen
aplicar a : y
Definiciones
Dominio, Dom(f)
Conjunto de valores x para los que
existe la función.
Discontinuidades
Valores del Dom(f) para los que la
función es discontinua
Asíntotas
verticales ; x=a
Valores del Dom(f) donde
lim f ( x)
Asíntotas
horizontales ;
y=a
xa
Donde a se calcula
a lim f ( x)
x
f ( x)
m lim
x x
b lim f ( x) mx
Puntos de corte
con el eje X
Son las soluciones de la ecuación :
f(x)=0
Puntos de corte
con el eje Y
Valores que toma la función cuando
x=0
x
Soluciones de la ecuación:
f'(x)=0. Cada caso se estudiará
según el apartado siguiente.
Página
91
2
Dom(f)=R - {1}
Para x = 1 la función es discontinua,
porque el límite cuando x tiende a 1 es
infinito y la función no existe en x = 1
lim
x
x 1
x 1
2
Luego la asíntota vertical : x=1
x
a lim
x
x 1
2
0
Luego la asíntota horizontal y=0
x
x
x x 1
2
0
x
b lim
0
x
0
2
x x 1
x
x 1
2
0 x0; y0
x = 0 ; y=0
y '( x)
Máximos y
mínimos
relativos
x 1
La función no existe cuando el
denominador es 0, por tanto :
m lim
Asíntotas
oblicuas ; rectas
de ecuación :
y = m x +b
x
x2 1
x 1
4
0 x 1
Para x=1, la función no existe
Para x= -1
1
y
0.25
2
1 1
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Regiones de
crecimiento o
decrecimiento de
la función. Con
esta información
se determina de
qué tipo son los
puntos en los
que la derivada
se hace 0.
Las regiones se determinan sobre el
eje X, entre los valores para los que
la derivada es 0
o no existe.
Representación
gráfica
Se utiliza toda la información que
proporciona la tabla
Aplicación de la derivada al cálculo de límites
Los límites de formas indeterminadas que no pueden resolverse mediante la factorización,
generalmente se resuelven en matemática por la conocida Regla de L´Hôpital, que contiene en su
estructura el concepto de derivada.
Teorema de L´Hôpital
Supongamos que las funciones f y g están definidas y son derivables en cierto entorno de a . Si
lim f ( x) lim g ( x) 0 , y g ( x) 0 en cierto entorno de a , entonces, si existe lim
x a
x a
x a
f ( x)
(finito o
g ( x)
f ( x)
f ( x)
f ( x)
, y se cumple que: lim
= lim
.
x
a
x
a
g ( x)
g ( x)
g ( x)
La Regla de L´Hôpital también es válida en el caso que las funciones f y g no están definidas en
a , pero lim f ( x) 0 y lim g ( x) 0 .
infinito), existe también lim
x a
x a
x a
Si f (a) g (a) 0 , y f (x) y g (x) satisfacen las condiciones puestas sobre las funciones f y g
, podemos aplicar la Regla de L´Hôpital a
f ( x)
f (c)
f ( x)
, y obtenemos: lim
= lim
; aplicar
x a g ( x )
x a g ( x )
g (c)
sucesivamente la derivada hasta que la indeterminación desaparézcala.
Ejemplos
1. Calcular:
Página
92
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
a.
x 2 1 ln x
ex e
lim
x 1
b. lim
x 0
x sen x
x3
c. lim
x 1
x3 3x 2 2
x3 4 x 2 3
Solución:
x 2 1 ln x
ex e
a) lim
x 1
En este caso estamos ante la indeterminación
0
2
2
, pues lim ( x 1 ln x) 1 1 0 0 , y
x 1
0
lim (e x e) e1 e 0
x 1
Resolvemos aplicando la Regla de L´Hôpital:
1
2x
x 2 1 ln x
( x 2 1 ln x)
x 3
lim
lim
lim
x
x
x
x1
x 1
x 1
e e
(e e)
e
e
x sen x
( sen x)
1
sen x 1
1 cos x
b) lim
= lim
lim
lim
3
2
x 0
x 0
x 0
x
6x
6 x 0 x
6
3x
x3 3x 2 2
3x 2 6 x 3 6 3
lim
=
x 3 4 x 2 3 x 1 3 x 2 8 x 3 8 5
c) lim
x 1
sen
2. Hallar: lim
x
Solución:
4
x
1
x
4
4
4
2 cos
x lim x
x lim 4 cos 4 4 lim
1
1
x
x
x
x
2
x
x
sen
lim
x
4
cos (4)(1) 4
x
El teorema anterior es válido si se sustituye la exigencia de lim f ( x) lim g ( x) = 0 por lim f ( x)
x a
x a
xa
lim g ( x) = , y se llama, por extensión, Regla de L´Hôpital.
x a
Ejemplos
Hallar:
a) lim
x 0
ln x
1
x
b)
lim
x
x2
ex
Solución:
a) En este caso estamos ante la indeterminación
, pues lim ln x , y
x 0
Página
93
lim
x 0
1
.
x
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Resolvemos aplicando la Regla de L´Hôpital:
1
2
ln x
x lim x 0
lim
= lim
x
x 0 1
x 0 1
x 0
2
x
x
2
x
2x
2
b) lim
= lim
lim
0
x
x
x
x e
x e
x e
Existen otras formas indeterminadas, 0. e , que pueden transformarse en las formas
, y aplicar la Regla de L´Hôpital.
Si queremos calcular lim f ( x).g ( x) y
0
0
ó
x a
lim f ( x) 0 y lim g ( x) , entonces,
x a
f ( x)
, y por tanto, lim f ( x).g ( x) = lim
1
x a
x a
g ( x)
g ( x)
Además, f ( x).g ( x) =
, y es un límite de la forma
1
f ( x)
f ( x).g ( x) =
x a
f ( x)
0
, y ahora es de la forma .
1
0
g ( x)
.
En dependencia del límite que se esté calculando, se hará una u otra de las transformaciones
anteriores, siguiendo el criterio que la aplicación de la Regla de L´Hôpital simplifique el proceso de
determinación del límite.
Ejemplos
Calcular:
2
2
a) lim x ln x
1
1
x 1 ln x
b) lim
x 0
x 1
Solución:
2
2
a. Observemos que lim x 0 , y lim ln x Luego, estamos ante una indeterminación del
x 0
x 0
tipo 0. . Transformando,
2x
2
2
ln
x
lim x 2 ln x 2 = lim
lim x lim x 2 0
1
2 x x 0
x 0
x 0
x 0
4
2
x
x
x2
2
2
Observe que lim x ln x = lim
, pero esta transformación es menos recomendable en
1
x 0
x 0
ln x 2
1
este caso en particular, pues la derivada de
es mucho más compleja que, simplemente, la
ln x 2
Página
94
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
derivada de ln x 2 .
1
1
x 1 x 1 ln x
b) lim
No existe una forma única de proceder para resolver indeterminaciones del tipo . En este
caso, se debe efectuar la resta:
ln x ( x 1)
ln x x 1)
1
1
= lim
= lim
lim
x 1 ( x 1) ln x
x 1 x 1 ln x x 1 ( x 1) ln x
Aquí podemos observar que: lim (ln x x 1) 0 y lim ( x 1) Lnx 0 Luego, la
x 1
x 1
indeterminación se ha transformado en una del tipo
0
. Basta entonces resolver
0
ln x x 1
lim
x 1 ( x 1) ln x
ln x x 1
lim
= lim
x 1 ( x 1) ln x x 1
1
1
x
= lim
1.ln x ( x 1). 1 x 1
x
1
1
2
x2
x
1 x ( x 1) lim x 1
x 1 2
2
x
x
x
1
1
lim
x 1 x 1
2
Aplicación de la derivada a problemas de optimización
Muchos de los problemas que se presentan en la práctica diariamente, están relacionados de una
forma u otra, con encontrar los valores máximos y mínimos de una función, y más aún, determinar
para qué valores de la variable independiente se alcanzan estos. Estos problemas se llaman, en
general, problemas de optimización. Se aplican en diferentes contextos, permitiendo resolver
problemas de optimización geométricos y económicos entre otros.
En términos generales, un problema de optimización consiste en encontrar el valor mínimo o
minimizar, o encontrar el valor máximo o maximizar, una cierta función, de tal forma que satisfagan
ciertas condiciones dadas.
La solución o soluciones óptimas son aquellas para las cuales se satisfacen las restricciones del
problema y el valor de la función sea mínimo o máximo.
La función que representa el problema de optimización se le llama función objetivo.
Fases en la solución de un problema de Optimización
1. Planteamiento del problema
2. Formulación Matemática (construir la función objetivo si no se da explícitamente)
3. Análisis del comportamiento de la función objetivo (puede incluir su representación gráfica)
4. Obtención de las soluciones
Ejemplos
1.
Para el producto de un monopolista la función de demanda es
valor de p para el cual se obtiene el ingreso máximo.
Página
95
x 10,000e0.02 p . Calcular el
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Solución
I px 10, 000 pe
0.02 p
I ( x) 10, 000 pe
I '( x)
; p0
0.02 p
(0.02) e
0.02 p
10, 000e
0.02 p
( 0.02 p 1)
10, 000(1 0.02 p)
1
100
0 1 0.02 p 0 p
50 . Único valor crítico en (0, )
0.02 p
0.02
2
e
I
(0,50)
(50, )
I ( p)
+
-
I ( p)
Creciente
Decreciente
I ( p) es creciente en (0,50) y decreciente en (50, )
Existe máximo relativo en p 50
Como es el único extremo local en (0, ) es también máximo absoluto en ese intervalo. Por tanto,
se obtiene el máximo ingreso con p = $50/unidad.
2.
Una empresa produce mensualmente x toneladas de un metal precioso con un costo total C
1
dado por C ( x) 10 75 x 5 x 2 x3 Evaluar el nivel de producción x donde el costo marginal
3
alcanza su mínimo.
Solución
Costo marginal C '( x) 75 10 x x 2 . Esta es la función para la cual queremos obtener un máximo:
C ''( x) 10 2 x 0 2 x 10 x 5 . Único valor crítico en (0, ) .
C '''( x) 2 0 , luego entonces existe un mínimo local y también absoluto en x 5 .
Por lo tanto para que el ingreso marginal sea mínimo el nivel de producción debe ser de 5
unidades.
3.
Para el producto de un monopolista, la función demanda es p
promedio es C 0.50
50
, y la función de costo
x
100
.
x
a) Evaluar el precio y la producción que maximizan la utilidad.
b) A este nivel, demostrar que el ingreso marginal es igual al costo marginal.
Solución
100
50
a) U I C;
I px
C Cx 0.5
x 0.5x 100 .
x 50 x ;
x
x
25
25
U ( x) 50 x 0.5x 100 50 x 0.5 x 100 U '( x) 25 x 1/2 0.5
0.5 0
0.5 .
x
x
25
x
50 x 2,500 . Único valor crítico en (0, ) .
0.5
25
25
U ''( x) x 3/2
U (2,500) 0 , luego existe un máximo local y también absoluto en
2
2 x3
2,500.
Página
96
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Entonces, para obtener la máxima utilidad posible se deben fabricar y vender 2,500 unidades a un
50
50
precio de p
$1/unidad.
2,500 50
25
25
25 1
b) I ( x) 25 x 1/2
I (2,500)
0.5;
C '( x) 0.5 C '(2,500) 0.5 .
x
2,500 50 2
Por lo tanto el ingreso marginal y el costo marginal son iguales cuando el nivel de producción es de
2,500 unidades, es decir cuando la utilidad es máxima.
4. Un fabricante ha determinado que, para cierto producto, el costo promedio por unidad está dado
por C 2 x 36 x 210
2
200
, para 2 x 10 , en donde x está en miles de unidades y C en
x
dólares.
a) Calcular a qué nivel dentro del intervalo 2,10 debe fijarse la producción para minimizar el
costo total y cuál es el costo total mínimo.
b) Si la producción se encontrara dentro del intervalo 5,10 , calcular qué valor de x minimizaría el
costo total.
Solución
C ( x) Cx 2 x3 36 x2 210 x 200 C ( x) 6 x 2 72 x 210 6( x 2 12 x 35) 6 x 7 x 5 .
Valores críticos x 5,
x7.
C( x) 12 x 72 12( x 6) C(5) 0; C(7) 0 . Por lo tanto
existe un máximo local en x = 5 y un mínimo local en x = 7.
a) En el intervalo 2,10 , como los dos valores críticos pertenecen al intervalo, no se puede
asegurar que el mínimo absoluto ocurra en x = 7, luego se requiere evaluar la función en esos
valores críticos y en los extremos del intervalo:
C(2) 2(2)3 36(2)2 210(2) 200 92;
C(5) 200;
C(7) 192;
C(10) 300 .
Por lo tanto el costo es mínimo cuando se fabrican 2,000 unidades. Costo mínimo: 92 dólares.
b) En el intervalo 5,10
C(5) 200;
C(7) 192;
C(10) 300 . El 2 no pertenece al intervalo.
Por lo tanto el costo es mínimo cuando se fabrican 7,000 unidades. Costo mínimo: 192 dólares.
5. Se quiere inscribir un rectángulo dentro de un semicírculo de radio 2. ¿Cuál es el área más
grande que puede tener el rectángulo y cuáles son sus dimensiones?
Página
97
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Según se muestra en la figura tenemos:
Largo del rectángulo: 2x
Altura:
4 x2
La función a maximizar es el área del rectángulo, es decir,
A( x) 2 x 4 x 2
Hallemos los puntos críticos, derivando e igualando a cero:
A( x) 2 x 4 x 2
A '( x)
2 x 2
2 4 x 0
4 x2
2 x 2 8 2 x 2 0
4 x 2 8
x2 2
2
2 x 2 2(4 x 2 )
4 x2
0
x 2
A( 2 ) 2 2 4 2 2( 2 ) 2 4
A( 2 ) 2( 2 ) 4 2 2( 2 ) 2 4 ( Area negativa )
Los valores extremos se presentan en: x = 2 y x = - 2
A(2) 2(2) 4 2 2 0 A(2) ( Area cero)
La mayor área del rectángulo se produce cuando x
2 y el área es de 4 unidades cuadradas.
Respuesta:
De lo anterior concluimos que las dimensiones del rectángulo de mayor área son:
Largo: 2 2
Alto:
2
6. Se desea construir una caja abierta (sin cara superior) y de base cuadrada con 108 pulgadas
cuadradas de material. ¿Cuáles serán las dimensiones de la caja para que el volumen sea
máximo?
Solución:
Página
98
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Volumen de la caja: V x 2 h (Función a maximizar)
Como esta función tiene dos variables (x, h) debemos usar los datos del
problema para eliminar una de ellas.
El material usado se obtiene sumando el área de la base y el área de las
cuatro caras laterales, así:
Área de la base: x 2
Área de cada cara lateral: xh
S x 2 4 xh 108
Área total de la superficie:
Hallando h en esta ecuación tenemos:
4 xh 108 x 2
h
108 x 2
4x
, 0 x 108
Sustituyendo h en la ecuación de volumen tenemos:
108 x 2
x3
V ( x) x 2 (
) 27 x
4x
4
Derivando e igualando a cero:
V ' ( x) 27
3x 2
0
4
,
3x 2 108
,
x 2 36
, x 6
Solo tomamos el valor positivo de x porque se trata de una longitud
Valor crítico: x = 6
Para este valor crítico, hallemos h:
h
108 x 2 108 36 72
3
4x
24
24
Respuesta: las dimensiones de la caja son:
Longitud de la base: x = 6 pulgadas.
Altura de la caja: h = 3 pulgadas.
Volumen de la caja: V x 2 h = 36(3) = 108 pulgadas cúbicas (Obsérvese la gráfica)
Página
99
I I - 2011
UNIDADES TECNOLÓGICAS DE SANTANDER
Nota: Usando el criterio de la segunda derivada se puede probar que, en efecto, los valores de x y
h corresponden al máximo volumen.
Página
100
I I - 2011