ma1010-27

Vectores de Coordenadas y Cambio de Base
Departamento de Matemáticas, CCIR/ITESM
9 de febrero de 2011
Índice
27.1. Introducción . . . . . . . . . . . . .
27.2. Vector de coordenadas . . . . . . .
27.3. Vector de Coordenadas y Rm . . .
27.4. Matriz de transición: Introducción
27.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
4
5
Introducción
En este tema se presenta el concepto de vector de coordenadas. Este concepto surge de la necesidad de
introducir nuevos sistemas coordenados o sistemas coordenados que mejor se adapten a una situación.
27.2.
Vector de coordenadas
Sea V un espacio vectorial de dimensión finita con base B = {v1 , . . . , vn }. Según un teorema anterior,
para cada v ∈ V existen escalares únicos c1 ,. . . ,cn tales que:
v = c1 v1 + · · · + cn vn
Definición 27.1
El vector en Rn cuyas componentes son los coeficientes de v, expresado como [v]B , se llama vector
de coordenadas o vector coordenado de v con respecto a B:


c1


[v]B =  ... 
cn
Nota
Observe que [v]B se modifica cuando cambia la base B. También [v]B depende del orden de los elementos de
B. Mantendremos fijo este orden usando siempre una base ordenada: este concepto se referirá a una base que
a pesar de ser conjunto se considerará en un orden determinado. Recuerde que en la definición matemática de
conjunto, el orden de los elementos no afecta el conjunto, sin embargo, en la definición de base ordenada el
orden es importante.
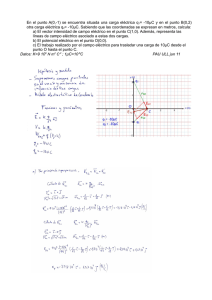
Teniendo disponible una gráfica a veces es posible determinar con relativa facilidad los vectores de coordendas.
4
2
0
-6
-4
-2
0
2
4
6
-2
-4
Figura 1: Nuevo Sistema Coordenado
Ejemplo 27.1
Si
B=
Se tiene
3
3
=
B
2
1
2
1
−1
,
1
−3
−1
,
=
0
1
B
Para ello vea la figura 1.
Ejemplo 27.2
Determine el polinomio p(x) sabiendo que su vector de coordenadas respecto a la base
B = {v1 = 1 − 7 x, v2 = −5 − 4 x}
es
[p(x)]B =
−6
2
Solución
Recuerde que el vector de coordenadas se forma con los coeficientes de la combinación lineal de los elementos
de la base para dar el vector: por tanto
p(x) = −6 v1 + 2 v2 ,
es decir
p(x) = −6 (1 − 7 x) + 2 (−5 − 4 x) ,
por tanto
p(x) = −6 + 42 x − 10 − 8 x = −16 + 34 x Ejemplo 27.3
Determine la matriz m sabiendo que su vector de coordenadas respecto a la base
−3
5
7
0
1 −1
−7 −3
B=
,
,
,
1 −7
−5 −6
−1 −4
−3 −2
2
es
[m]B

−1
 −2 

=
 −4 
3

Solución
Directamente de la definición de vector de coordenadas:
m = −1 −31 −75 − 2 −57 −60 + 4
desarrollando los productos
m=
3
−1
−5
7
+
−14
10
0
12
+
1
−1
+3
−1
−4
4
−4
−4 −16
+
−21
−9
por tanto
m=
−28 −18
−4 −3
Ejemplo 27.4
En P1 , determine el vector de coordenadas del polinomio
p(x) = −2 − 5 x
respecto a la base ordenada
B = {v1 = 2 − 4 x, v2 = 4 + x}
Solución
Buscamos escalares c1 y c2 tales que:
−2 − 5 x = p(x) = c1 (2 − 4 x) + c2 (4 + 1 x)
Es decir
−2 − 5 x = (2 c1 + 4c2 ) + (−4 c1 + 1 c2 )x
Esto se convierte en el sistema
2 c1 + 4 c2 = −2
−4 c1 + 1 c2 = −5
Formando la matriz aumentada y reduciéndola
2 4 −2
1 0
1
→
−4 1 −5
0 1 −1
Por tanto, c1 = 1 y c2 = −1 y
[p(x)]B =
1
−1
Ejemplo 27.5
En M2×2 , determine el vector de coordenadas de la matriz
−4 −1
m=
5
4
3
−7
−3
−3
−2
−9
−6
respecto a la base ordenada
B=
4
0
−4
−5
−3
,
0
−5
−1
5 −4
−5 −2
,
,
−1
5
−2
1
Solución
Buscamos c1 , c2 , c3 , y c4 tales que:
−4 −1
4 −4
−3
0
−5 −2
5 −4
= c1
+ c2
+ c3
+ c4
5
4
0 −5
−1 −5
−1 −2
5
1
Es decir, tales que:
−4 −1
5
4
=
4c1 − 3 c2 − 5 c3 + 5 c4 −4c1 + 0 c2 − 2 c3 − 4 c4
0c1 − 5 c2 − 1 c3 + 5 c4 −5c1 − 2 c2 − 2 c3 + 1 c4
Igualando cada entrada se convierte en el sistema:
+
−
+
−
4 c1
4 c1
0 c1
5 c1
−
+
−
−
3 c2
0 c2
5 c2
2 c2
−
−
−
−
5 c3
2 c3
1 c3
2 c3
+
−
+
+
5 c4
4 c4
5 c4
1 c4
= −4
= −1
=
5
=
4
Al formar la matriz aumentada y reducirla:

4 −3
 −4
0

 0 −5
−5 −2


13
1 0 0 0 − 12
−5
5 −4

 0 1 0 0
−2 −2 −1 
→

5 
−1
5
 0 0 1 0

−2
1
4
0 0 0 1
1
6
5
4
17
12







Por tanto,

[m]B
27.3.
13
− 12
1
6



=


5
4
17
12




 

Vector de Coordenadas y Rm
Los siguiente resultado permite trasladar los conceptos de dependencia lineal y espacios generados a cualquier base. También justifica nuestro proceso de vectorización para operar los conceptos de espacios generados
y dependencia lineal.
Teorema
Sea B una base ordenada de un espacio vectorial V de dimensión finita. Sean u, u1 , u2 , . . . , um
vectores en V . Entonces, u es una combinación lineal de u1 , ...., um en V , si y sólo si [u]B es una
combinación lineal de [u1 ]B , . . . , [um ]B en Rm . Además, para los escalares c1 ,. . . ,cm
u = c 1 u1 + · · · + c m um
si y sólo si
[u]B = c1 [u1 ]B + · · · + cm [um ]B
4
Figura 2: Múltiples Sistemas Coordenados
Teorema
Sea B una base ordenada de un espacio vectorial n dimensional V . Entonces, {u1 , . . . , um } es
linealmente independiente en V si y sólo si {[u1 ]B , . . . , [um ]B } es linealmente independiente en
Rn .
27.4.
Matriz de transición: Introducción
Sean B = {v1 , . . . , vn } y B ′ = {v′ 1 , . . . , v′ n } dos bases ordenadas de un espacio vectorial de dimensión
finita. Sea P la matriz n × n cuyas columnas son [v1 ]B′ , . . . , [vn ]B′ :
P = [[v1 ]B′ [v2 ]B′ · · · [vn ]B′ ]
Entonces P es invertible y ésta es la única matriz en la que para todo v ∈ V :
[v]B′ = P [v]B
Definición 27.2
La matriz P del resultado anterior se denomina matriz de transición o matriz de cambio de base
de B a B ′ .
Teorema
Si P es la matriz de transición de B a B ′ , entonces P−1 es la matriz de transición de B ′ a B.
Ejemplo 27.6
En R2 , determine la matriz de transición de la base:
0
1
B=
,
1
0
5
a la base:
′
B =
−6
−7
0
,
5
Solución
Lo que debemos hacer es determinar el vector de coordenas de cada uno de los elementos de la base vieja en
función de la base nueva. Aunque la versión oficial consiste en trabajar con los vectores uno por uno. Es
posible trabajarlos un solo paquete combo: Se forma la matriz aumentada:
[Basenueva |BaseV ieja ]
Y se aplica a esta matriz aumentada el proceso de Gauss-Jordan. Al aplicar Gauss-Jordan quedarán en
el lugar adecuado los vectores de coordenadas de cada un de los vectores de la base vieja respecto a la base
nueva: es decir,
h
i
Basenueva |BaseVieja → [I|P]
Aplicando esta idea al problema:
−6 0 0 1
−7 5 1 0
→
1 0
0 −1/6
0 1 1/5 −7/30
Por tanto,
P=
0 −1/6
1/5 −7/30
6