UNIDAD I: ECUACIONES E INECUACIONES
SESIÓN 03: Inecuaciones polinómicas y racionales
I.
Resuelva las siguientes inecuaciones polinómicas:
3
− x + 81x < 0
1)
Solución:
Multiplicando por (-1)
3
x − 81x > 0
2
x( x − 81) > 0
x( x − 9)( x + 9) > 0
Los puntos críticos son -9, 0, 9
-
-
+
-9
+
9
0
C.S : ]−9;0[ ∪ ]9; +∞[
x3 − 4 x2 − 5x ≥ 0
2)
Solución:
Factorizando
x ( x 2 − 4 x − 5) ≥ 0
x ( x − 5 )( x + 1) ≥ 0
-
+
+
-
-1
5
0
C .S : [ − 1, 0 ] ∪ [5, +∞ [
− x 3 + 81x ≥ 0
3)
Solución:
La inecuación dada la expresamos en forma:
x ( x 2 − 81) ≤ 0
x ( x − 9 )( x + 9 ) ≤ 0
-
+
-9
1
0
C .S : [ −∞ , − 9 ] ∪ [ 0, 9 ]
MATEMÁTICA BÁSICA - INGENIERIA
+
9
x 4 + 12 x3 − 64 x 2 > 0
4)
Solución:
Factorizando
x 2 ( x 2 + 12 x − 64 ) > 0
x 2 ( x + 16 )( x − 4 ) > 0
Como x 2 ≥ 0 , entonces la inecuación la escribimos
( x + 16 )( x − 4 ) > 0
-
+
+
-16
4
C .S : ]−∞ , − 16[ ∪ ]4, +∞ [
3x 2 + 4 < x 4 + 3x3 + 3x
5)
Solución:
x 4 + 3x3 − 3x 2 + 3x − 4 > 0
Aplicando Ruffini:
1
3 -3 3 -4
1
1
1 4
-4
-4
1 0
Tenemos:
( x − 1)( x + 4 ) ( x 2 + 1) > 0
4 1
1 4
0 -4
1 0
4
0
+
+
–∞
+∞
1
-4
C .S : ]−∞ , − 4[ ∪ ]1, ∞ [
( x + 2 )( x − 1) ( x − 6 ) ≤ 0
3
6)
Solución:
Puesto que ( x − 1) ≥ 0 , la inecuación es equivalente a, ( x + 2 )( x − 1)( x − 6 ) ≤ 0
2
-
-
+
-2
1
+
6
C .S : ]−∞ , − 2 ] ∪ [1, 6 ]
2
MATEMÁTICA BÁSICA - INGENIERIA
(x
7)
2
+ 1) ( x + 1)
2
( x − 2 )( x − 3)
3
<0
Solución:
2
Puesto que x + 1 ≥ 0;
( x − 2)( x − 3) < 0
( x + 1)2 ≥ 0
2
y ( x − 3) ≥ 0 , la inecuación es equivalente a,
-
+
+
2
3
C.S =< 2,3 >
( x 2 + 22 )( x − 1)3 ( x 2 − 9) ≥ 0
8)
Solución:
La inecuación es equivalente a, ( x − 1)( x + 3)( x − 3) ≥ 0
-
-
+
-3
+
3
1
C .S : [ − 3,1] ∪ [3, +∞ [
x 5 − 5 x 4 + 2 x 3 + 14 x 2 − 3 x − 9 ≤ 0
9)
Solución:
Factorizando por Ruffini:
1 -5
1
2 14 -3 -9
9
0
1 -4 -2 12
1 -4 -2 12 9
-1 5 -3 -9
1 -5 3 9 0
3
3 -6 -9
-2
1
-3 0
-1
2
Tenemos, ( x − 1)( x + 1)( x − 3)( x − 2 x − 3) ≤ 0 , lo cual es equivalente a
2
2
( x − 1)( x + 1) ( x − 3) ≤ 0
2
2
Puesto que ( x + 1) ≥ 0 y ( x − 3) ≥ 0 (tenga en cuenta que x = -1 y x = 3, satisfacen estas
inecuaciones), la inecuación la expresamos
x −1 ≤ 0
x ≤1
3
MATEMÁTICA BÁSICA - INGENIERIA
1
3
C.S : ]−∞,1] ∪ {3}
10)
(x
2
+ x − 6 )( 4 x − 4 − x 2 ) ≤ 0
Solución:
( x + 3)( x − 2)( x 2 − 4 x + 4) ≥ 0
( x + 3)( x − 2)( x − 2) 2 ≥ 0
Esta inecuación es equivalente a, ( x + 3)( x − 2) ≥ 0
+
+
–∞
2
-3
+∞
C .S : ]−∞ , − 3] ∪ [ 2, ∞ [
11) −3 x 3 − x 2 + x − 1 < 0
Solución:
Si multiplicamos por (-1) la inecuación, tenemos 3 x 3 + x 2 − x + 1 > 0 , luego aplicamos Rufini.
3
1
-1
1
-3 2 -1
3 -2 1 0
-1
( x + 1) ( 3x 2 − 2 x + 1) > 0
Como la ecuación 3 x 2 − 2 x + 1 = 0 no tiene soluciones reales ya que su discriminante es menor
que cero, entonces no lo consideramos en la solución de la inecuación. Por tanto
x +1 > 0
x > −1
-1
C .S =< − 1, +∞ >
4
MATEMÁTICA BÁSICA - INGENIERIA
II.
Resuelva las siguientes inecuaciones racionales:
3x + 5
≤3
2x + 1
1)
Solución:
3x + 5
−3≤ 0
2x +1
⇔
3x + 5 − 6 x − 3
≤0
2x +1
2 − 3x
≤0
2x +1
2 − 3x
1
≤ 0 , es equivalente a la inecuación (3 x − 2)(2 x + 1) ≥ 0 , para x ≠ −
2
2x +1
2
1
Las raíces de la ecuación (3 x − 2)(2 x + 1) = 0 son x = ; x = −
3
2
La inecuación
+
+
–∞
+∞
2/3
-1/2
La solución es la unión de los intervalos donde aparece el signo (+), es decir
1
2
C.S :< −∞, − > ∪ ; ∞ >
2
3
2
4
≥
1 − x 14 x
2)
Solución:
2
4
−
≥0
1 − x 14 x
28 x − 4 + 4 x
≥0
(1 − x)14 x
32 x − 4
≥ 0 , es equivalente a la inecuación (32 x − 4)( x − 1)14 x ≤ 0 , para
(1 − x)14 x
1
x ≠ 0 y 1 .Las raíces de la ecuación (32 x − 4)( x − 1)14 x = 0 son x = 0; x = y x = 1
8
La inecuación
-
-
+
0
1/8
1
C.S :< −∞, 0 > ∪ ,1 >
8
5
MATEMÁTICA BÁSICA - INGENIERIA
+
1
x 2 − 5x + 6
≥0
x 2 + x − 42
3)
Solución:
( x − 2)( x − 3)
≥0
( x + 7)( x − 6)
Los puntos críticos son x = 2; x = 3, x = -7 y x = 6.
-
+
-
+
2
-7
3
+
6
C.S :< −∞; −7 > ∪[ 2,3] ∪ < 6, ∞ >
5x − x 2
≤0
x+7
4)
Solución:
La inecuación
x2 − 5x
≥ 0 es equivalente a la inecuación x ( x − 5)( x + 7) ≥ 0
x+7
-
+
-7
-
+
0
5
C.S :< −7;0] ∪ < 5; +∞ >
1
1
<
x+5 x−4
5)
Solución:
( x − 4) − ( x + 5)
<0
( x + 5)( x − 4)
−9
<0
( x + 5)( x − 4)
9
>0
( x + 5)( x − 4)
+
–∞
+
-5
4
C .S :< −∞; −5 > ∪ < 4; ∞ >
6
MATEMÁTICA BÁSICA - INGENIERIA
+
x
3
−
≥0
x −4 x+2
6)
2
Solución:
x − 3( x − 2)
≥0
x2 − 4
−2 x + 6
≥0
( x + 2)( x − 2)
+
-2
+
2
3
(2 x − 6)( x + 2)( x − 2) ≤ 0
C .S :< −∞; −2 > ∪ < 2; 3]
UNIDAD I: ECUACIONES E INECUACIONES
SESIÓN 04: Aplicaciones de las inecuaciones polinómicas y racionales
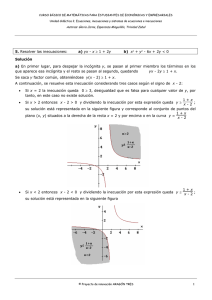
1. Pasados " t " minutos después de introducir un bactericida experimental en cierto cultivo, el
número de bacterias está dado por N = 102 000 + 2 000 . Determinar a partir de qué momento el
t +1
número de bacterias está por debajo de 4000 .
Solución:
Modelamos la inecuación:
10000
+ 2000 < 4000
t 2 +1
Pasamos todo al primer miembro:
10000
− 2000 < 0
t 2 +1
Sacamos el denominador común:
10000 − 2000t 2 − 2000
<0
t 2 +1
Operamos en el numerador:
− 2000t 2 + 8000
<0
t 2 +1
Factorizamos en el numerador:
(
)
− 2000 t 2 − 4
<0
t 2 +1
Pasamos a dividir al segundo miembro:
7
MATEMÁTICA BÁSICA - INGENIERIA
t2 − 4
>0
t 2 +1
Factorizamos nuevamente el numerador:
(t + 2)(t − 2) > 0
t 2 +1
Hemos obtenido los factores, ahora igualamos a cero cada uno y despejamos:
t +2 = 0
t −2 = 0
t = −2
t =2
t2 + 1 = 0
( raices complejas
)
Este térmi no siempre será positivo
+
,∞
+
–2
2
*∞
C.S = −∞; −2 ∪ 2; +∞
Dado que el tiempo es positivo, entonces la solución al problema será: 2;∞ .
INTERPRETACIÓN: el número de bacterias será menor a 4000, si el tiempo es mayor a 2 minutos.
2. Una planta de empaque desea diseñar cajas sin tapa con un volumen de no más de 400 cm3. Para
tal diseño se utilizará una pieza de cartón de 12cm por 15 cm, se realizará cortes iguales y exactos
en las esquinas y finalmente se doblarán las solapas hacia arriba. Determinar el tamaño máximo
del corte que deben realizar en las esquinas de la pieza de cartón.
Solución: sea x : el corte igual y exacto que se dará en las esquinas del cartón.
x
12
x
15
El volumen debe ser menor a 400:
V ≤ 400
El volumen es largo por ancho por altura:
(15 − 2 x )(12 − 2 x )(x ) ≤ 400
Operamos:
4 x 3 − 54 x 2 + 180 x ≤ 400
Pasamos todo al primer miembro:
4 x 3 − 54 x 2 + 180x − 400 ≤ 0
Factorizamos el primer miembro:
(
)
2 2 x 3 − 27 x 2 + 90 x − 200 ≤ 0
Pasamos a dividir al segundo miembro:
2 x 3 − 27 x 2 + 90 x − 200 ≤ 0
Factorizamos nuevamente el primer miembro:
(x − 10)(2 x 2 − 7 x + 20) ≤ 0
Hemos obtenido los factores, ahora igualamos a cero cada uno y despejamos:
2012-2 MATEMÁTICA BÁSICA -INGENIERÍA
x − 10 = 0
2x 2 − 7x + 20 = 0
( raices complejas
)
Este término siempre será positivo
x = 10
_
,∞
+
10
+∞
C.S = ( −∞;10]
Dado - > 0, entonces C.S = ( 0;10]
Las medidas de la caja también son positivas, es decir que:
15 − 2 x > 0 ∧ 12 − 2 x > 0
⇒x<6
entonces la solución al problema será: ]0;6[ .
INTERPRETACIÓN: el tamaño máximo del corte que se debe dar en las esquinas del cartón debe
ser de 5cm (corte exacto).
3. La empresa de telecomunicaciones “Telemark” en su afán de expandirse, pone en promoción dos
planes de telefonía para el mes venidero. La demanda del primer plan está modelada a través de
1/ 2
1/ 2
la ecuación d1 =
y la demanda del segundo plan mediante la ecuación d 2 = −
; donde
x−3
x−5
" x " indica el número de ventas que a diario se realiza en la empresa. Determinar el número
mínimo de ventas que debe realizar a diario; para que la demanda del primer plan sea mayor a la
otra.
Solución: sea x : el número de ventas que la empresa realiza a diario.
Modelamos la inecuación:
1
1
−
2 > 2
x −3 x −5
Pasamos todo al primer miembro:
1
1
2 + 2 >0
x −3 x −5
Sacamos el denominador común:
1
(x − 5) + 1 (x − 3)
2
2
>0
(x − 3)(x − 5)
Operamos en el numerador:
x 5 x 3
− + −
2 2 2 2 >0
(x − 3)(x − 5)
x−4
>0
(x − 3)(x − 5)
Hemos obtenido los factores, ahora igualamos a cero cada uno y despejamos:
x−4 =0
x=4
x−3= 0
x=3
- -INGENIERÍA
+
2012-2 MATEMÁTICA BÁSICA
x −5 = 0
x=5
-
+
,∞
3
4
5
+∞
C.S = 3;4 ∪ 5; +∞
INTERPRETACIÓN: dado que el número de ventas es una variable discreta, entonces el número
mínimo de ventas deberá ser 6; para que el plan el primer plan sea mayor al segundo plan.
4. Un grupo de estudiantes decide asistir a un concierto. El costo de contratar a un autobús para que
los lleve al concierto es de $450, lo cual se debe repartir en forma uniforme entre los estudiantes.
Los promotores del concierto ofrecen descuentos a grupos que lleguen en autobús. Los boletos
cuestan normalmente $50 cada uno, pero se reducen 10 céntimos de dólar del precio del boleto
por cada persona que vaya en el grupo (capacidad máxima del autobús es 60). Determinar
cuántos estudiantes deben ir en el grupo; para que el costo total por estudiante sea menor a $54.
Solución: Sea -:el número de alumnos que van en el autobús.
Modelamos la inecuación:
Costo =
Costo del bus
+ Costo del boleto
número de estudiantes
C=
450
+ (50 − 0.10 x )
x
C=
450
+ 50 − 0.1x
x
El costo total debe ser menor a $54:
C < 54
450
+ 50 − 0.1x < 54
x
Pasamos todo al primer miembro:
450
+ 50 − 0.1x − 54 < 0
x
Sacamos el denominador común:
450 + 50 x − 0.1x 2 − 54 x
<0
x
Operamos en el numerador:
− 0.1x 2 − 4 x + 450
<0
x
Factorizamos el primer miembro:
(− 1)(0.1x 2 + 4 x − 450) < 0
x
Pasamos a dividir al segundo miembro:
0.1x 2 + 4 x − 450
>0
x
Factorizamos nuevamente el primer miembro:
2012-2 MATEMÁTICA BÁSICA -INGENIERÍA
(0.1x − 5)(x + 90) > 0
x
Hemos obtenido los factores, ahora igualamos a cero cada uno y despejamos:
0.1x − 5 = 0
x = 50
x + 90 = 0
x = −90
,∞
x=0
-
+
–90
0
0v
+
50
−∞
C.S = −90;0 ∪ 50; +∞
Dado que el número de alumnos es positivo y la capacidad del autobús, entonces el conjunto de
solución al problema será: ( 50;60] .
INTERPRETACIÓN: Para que el costo por estudiante sea menor a $54, el número de estudiantes
que debe ir en el autobús debe ser desde 51 hasta 60.
5. Para que un medicamento tenga efecto benéfico, su concentración en el torrente sanguíneo debe
ser mayor que cierto valor; llamado este último “nivel terapéutico mínimo”. Suponga que la
concentración “C” (mg/l) de cierto fármaco al transcurrir “t” horas después de su ingestión está
dada por C = 220t . Si el nivel terapéutico mínimo es de 4 mg/l, entonces dentro de cuánto tiempo
t +4
se excederá este nivel.
Solución:
Modelamos la inecuación:
20t
>4
t +4
2
Pasamos todo al primer miembro:
20t
−4>0
t +4
2
Sacamos el denominador común:
20t − 4t 2 − 16
>0
t2 + 4
Ordenamos en el numerador:
− 4t 2 + 20t − 16
>0
t2 + 4
Factorizamos en el numerador:
(− 4)(t 2 − 5t + 4) > 0
t2 + 4
Pasamos a dividir al segundo miembro:
t 2 − 5t + 4
<0
t2 + 4
Factorizamos nuevamente el numerador:
(t − 1)(t − 4) < 0
t2 + 4
Hemos obtenido los factores, ahora igualamos a cero cada uno y despejamos:
2012-2 MATEMÁTICA BÁSICA -INGENIERÍA
t −1 = 0
t −4 = 0
t =1
t =4
t2 + 4 = 0
( raices complejas
)
Este término siempre será positivo
−∞
1
4
*∞
C.S = 1;4
INTERPRETACIÓN: el nivel terapéutico mínimo se excederá entre la 1° y la 4° hora de la ingesta
del medicamento.
6. En un plaza de nuestra cuidad se desea construir una fuente rectangular de 12m de perímetro.
Según el reglamento para la construcción, las dimensiones deben ser cantidades exactas y que el
producto de la base por el cuadrado de la otra no debe ser mayor a 16m. Determinar la dimensión
máxima que deberá tener el ancho de la fuente.
Solución: sea x : la base de la fuente
y : El ancho de la fuente.
B
Por dato se tiene que el perímetro =12
⇒ 2 x + 2 y = 12
⇒ x+ y =6
⇒ x = 6 − y...[1]
2
Tenemos la condición que x. y ≤ 16...[2]
De [1] en [2]
2
⇒ (6 − y ) y ≤ 16
3
2
⇒ − y + 6 y − 16 ≤ 0
3
2
⇒ y − 6 y + 16 ≥ 0
2
⇒ ( y − 2)( y − 4 y − 8) ≥ 0
(
)
(
V .C : y = 2 1 − 3 ;2;2 1 + 3
,∞
(
)
)
281 − √3:
(
) )
C.S = 2 1 − 3 ;2 ∪ 2 1 + 3 ; +∞
2
0v
281 + √3:
*∞
(
) )
Dado que - > 0 entones el conjunto solución será C.S = ( 0;2] ∪ 2 1 + 3 ; +∞ .
De [1], se tiene que si x > 0 ⇒ y < 6 , entonces el conjunto de solución al problema es
2012-2 MATEMÁTICA BÁSICA -INGENIERÍA
)
C .S = ( 0;2] ∪ 2(1 + 3);6 .
INTERPRETACIÓN: la dimensión máxima (exacta) que debe tener el ancho es de 2m.
7. En las cercanías de una hoguera, la temperatura "T " en °C a una distancia de " x " metros desde
el centro de la hoguera; se determina mediante la ecuación racional T = 600000 . ¿A qué distancia
2
del centro del fuego, la temperatura será menor de 500 °C ?
x + 300
Solución:
Modelamos la inecuación:
600000
< 500
x 2 + 300
Pasamos todo al primer miembro:
600000
− 500 < 0
x 2 + 300
Sacamos el denominador común:
600000 − 500 x 2 − 150000
<0
x 2 + 300
Operamos en el numerador:
− 500 x 2 + 450000
<0
x 2 + 300
Factorizamos en el numerador:
(− 500)(x 2 − 900) < 0
x 2 + 300
Pasamos a dividir al segundo miembro:
x 2 − 900
>0
x 2 + 300
Factorizamos nuevamente el numerador:
(x + 30)(x − 30) > 0
x 2 + 300
Hemos obtenido los factores, ahora igualamos a cero cada uno y despejamos:
x + 30 = 0
x − 30 = 0
x = −30
x 2 + 300 = 0
( raices complejas
)
Este término siempre será positivo
x = 30
+
+
–∞
C.S = −∞; −30 ∪ 30; +∞
–30
30
+∞
Dado que la distancia es positiva, entonces el conjunto de solución al problema será: 30;+∞ .
INTERPRETACIÓN: Para una distancia mayor a 30m desde el centro de la fogata, la temperatura
será menor a 500 °C.
2012-2 MATEMÁTICA BÁSICA -INGENIERÍA
8. Al realizar un estudio en un sector minero se encontró un gran porcentaje de personas con niveles
elevados de plomo en la sangre. El instituto de salud pública decidió comenzar un tratamiento
con uno costoso medicamento a las persona que tengan un 6% de sangre contaminada. El
porcentaje que describe la cantidad de plomo en la sangre como efecto de “x” gramos del
2
medicamento, viene dado por la relación P =
x + 5x + 6
2
x + x +1
, con P expresado en %. ¿Al menos
cuántos gramos deben administrarse para que el porcentaje de plomo sea menor que 2%?
Solución: sea -:la cantidad de gramos de medicamento.
Modelamos la interrogante, mediante la inecuación:
2
x + 5x + 6
2
x + x +1
<2
2
2
⇒
x + 5 x + 6 − 2( x + x + 1)
⇒
− x + 3x + 4
2
x + x +1
<0
2
2
x + x +1
<0
2
x − 3x − 4
>0
2
x + x +1
( x − 4)( x + 1)
>0
⇒ 2
x + x +1
V .C : x = −1;4
⇒
2
( x + x + 1 = 0, es siempre positivo; tiene raices complejas)
,∞
−1
*∞
4
C.S = −∞; −1 ∪ 4; +∞
Dado que la los gramos de medicamento son positivos, entonces el conjunto de solución al
problema será: 4;+∞ .
INTERPRETACIÓN: podemos afirmar que se deben administrar un poco más de 4 gramos del
medicamento para que el porcentaje de plomo sea menor que 2 %.
Ξ
2012-2 MATEMÁTICA BÁSICA -INGENIERÍA