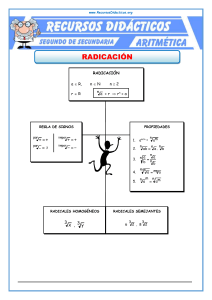
1.1 Radicales

DESARROLLO DE ACTIVIDADES PEDAGÓGICAS
Código: FOR-GA-83/Versión 2
IDENTIFICACIÓN DE LA ACTIVIDAD PEDAGÓGICA
PROGRAMA DE FORMACIÓN
UNIDAD DE APRENDIZAJE
ACTIVIDAD
OBJETIVOS
BACHILLERATO (9° GRADO)
ALGEBRA DE NOVENO
RADICALES OPERACIONES CON RADICALES ADICIÓN Y SUSTRACCIÓN
APRENDER LOS CONCEPTOS BASICOS MEDIANTE LOS CUALES SE PUEDEN REALIZAR OPERACIONES
Y DESARROLLAR EJERCICIOS DE RADICALES, ADICION Y SUSTRACCION
DESARROLLO DE LA ACTIVIDAD
1.1
Radicales
La radicación es la operación inversa de la potenciación. Si una potencia es:
an =b
La radicación es la operación que tiene que obtener
a conociendob y n. Se expresa:
n
−1
f : a =b → f : a = n b
Se llama raíz -nésima de un número realb a otro número reala cuya
Potencia n Ésima es igual ba
n
n
b =a
b : es el Radical
b : es el radicando
n: eselíndice
a :eslaraíz
Como consecuencia de las reglas sobre los signos de las potencias de exponente natural y base negativa tenemos que
Página
Si n = 2, es la raíz cuadrada y se acostumbra a omitir el índice
Si n = 3, es la raíz cúbica
Si n = 4, es la raíz cuarta y así sucesivamente
1
Un radical puede llevar coeficientes que formen parte de el como por ejemplo 3n b donde 3 es el coeficiente y forma parte del radical.
DESARROLLO DE ACTIVIDADES PEDAGÓGICAS
Código: FOR-GA-83/Versión 2
•
Toda raíz de índice impar de un número tiene el mismo signo que el radicando
3
8 = 2 ya que 23 = 8
−8 = −2 ya que (−2)3 = −8
Toda raíz de índice par de un número positivo tiene doble signo
16 = ±4 yaque 42 = (−4)2 = 16
Toda raíz de índice par y radicando negativo no es real
3
•
•
4
− 64 Ejercicios:
Calcula el valor de los siguientes radicales identificando en cada uno de ellos índice, radicando y raíz:
1.
9
2.
3
9.
−8
4
625
256
1
5
10.
729
11.
3
2.
3
125
12.
5
3.
4.
256
4
256
13.
14.
5.
5
81
6.
256
4
− 32
−
7776
3
−10
24
3 8
12
15. 0.00
5
0.064
16.
2
64
Página
1.
DESARROLLO DE ACTIVIDADES PEDAGÓGICAS
Código: FOR-GA-83/Versión 2
Definición de Adición:
Si los sumandos son del mismo signo, se suman los valores absolutos y al resultado se le pone el signo común.
Ejemplo:
3+5=8
(−3) + (−5) = −8
2.Si los sumandos son de distinto signo, se restan los valores absolutos (al mayor le restamos el menor) y al resultado se le pone el signo
del número de mayor valor absoluto.
Ejemplos
(− 3) + 5 = 2
3 + (−5) = −2
Definición de sustracción:
Restar un número es igual que sumar su opuesto.
a – b = a + -b El opuesto de b es -b
Ejemplo:
3 – 4 = 3 + -4 El opuesto de 4 es -4
En la resta, se cambia a suma y se escribe el opuesto del número que se está restando, entonces se siguen las reglas de la suma.
-2 - 5 = -2 + -5 El opuesto de 5 es –5
(- 2)+ (-5) = -7
Página
3
5 - ( -7) = 5 + 7 = 12 El opuesto de –7 es 7
DESARROLLO DE ACTIVIDADES PEDAGÓGICAS
Código: FOR-GA-83/Versión 2
RECURSOS Y EQUIPOS REQUERIDOS
Página
4
HUMANO, FÍSICO (TABLERO, MARCADORES, BORRADOR, PLAN DE CLASE Y GUIA DE DESARROLLO TEMATICO)