α α α

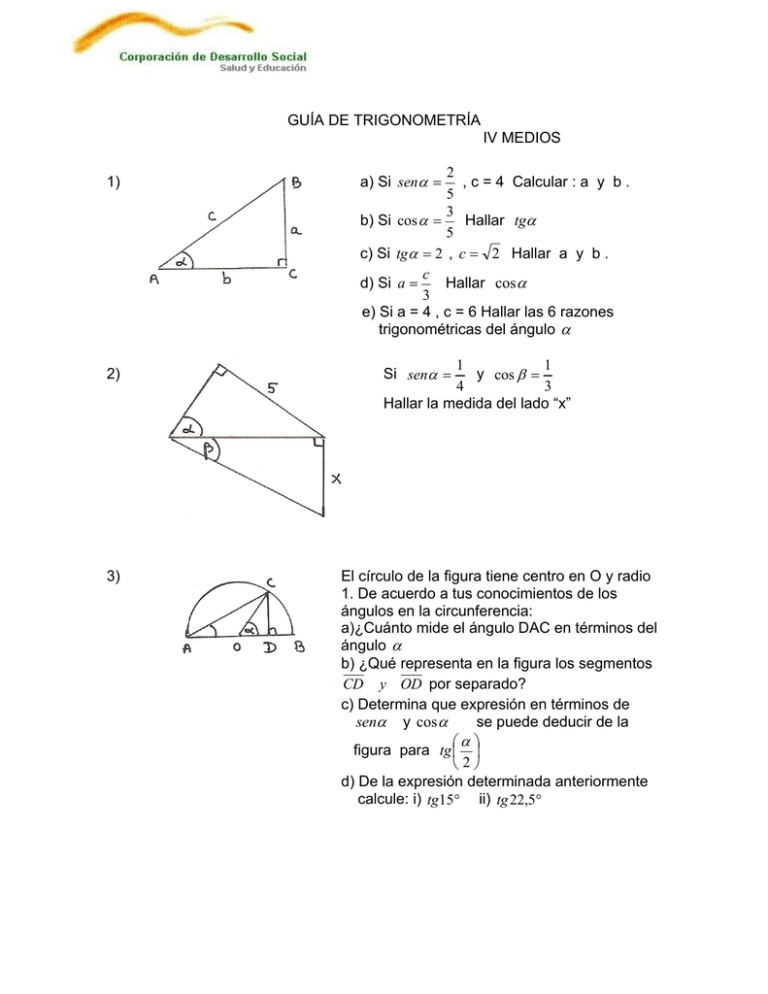
GUÍA DE TRIGONOMETRÍA
IV MEDIOS
1)
2)
3)
2
, c = 4 Calcular : a y b .
5
3
Hallar tgα
b) Si cos α =
5
c) Si tgα = 2 , c = 2 Hallar a y b .
c
d) Si a =
Hallar cos α
3
e) Si a = 4 , c = 6 Hallar las 6 razones
trigonométricas del ángulo α
a) Si senα =
1
1
y cos β =
4
3
Hallar la medida del lado “x”
Si senα =
El círculo de la figura tiene centro en O y radio
1. De acuerdo a tus conocimientos de los
ángulos en la circunferencia:
a)¿Cuánto mide el ángulo DAC en términos del
ángulo α
b) ¿Qué representa en la figura los segmentos
CD y OD por separado?
c) Determina que expresión en términos de
senα y cos α
se puede deducir de la
⎛α ⎞
figura para tg ⎜ ⎟
⎝2⎠
d) De la expresión determinada anteriormente
calcule: i) tg15° ii) tg 22,5°
4) Usando las identidades trigonométricas fundamentales, exprese en la forma
más simple:
1
1 − cos 2 α
c) sen 4α − cos 4 α − sen 2α
• ctgα
b) tgα +
2
tgα
1 − sen α
cos ecα
cos α
senα
senα
cos α
cos α
e)
f)
d) tg 3α •
+
+ tgα •
+
sec α
senα
1 + cos α 1 − cos α
1 + senα 1 − senα
tgα
tgα
ctgα
ctgα
h)
i)
g)
+
+
1 + sec α 1 − sec α
cos ecα + 1 cos ecα − 1
senα • sec α + cos α • cos ecα
⎡ senα + cos 2 α
⎤
tgα sec α
− cos α ⎥ k) 1 − sen 2α • sec 2 α − 1 l)
j) 1 + tgα • ⎢
−
cos α
sec α tgα
⎣
⎦
a)
m) 1 −
cos 2 α
1 + senα
n) 1 −
sen 2α
1 − cos α
5) Calcule: a) sen 2 45° − cos 2 45°
b) (tg 60° − tg 30°)
2
c)
tg 60°
tg 45° − tg 30°
d) sen 270° • cos 180 ° − sen 2 10° − cos 2 10°
2
2
e) (sen90° − cos 90°) − (cos 270° − sen180°)
6) Plantee y resuelve los siguientes problemas:
a) Desde un punto situado a 111 metros de un edificio, el ángulo de elevación
es de 30°.¿Cuál es la altura del edificio?
b) Desde un globo aéreo situado directamente sobre un pueblo C se obseva
un pueblo A , bajo un ángulo de depresión de 60°. Si la distancia entre A y
C es de 12 kilómetros. Calcular la altura a que se encuentra el globo.
c) Una persona arriba de un faro, a 20 metros sobre el nivel del mar , observa
con un ángulo de depresión de 30° a un bote. ¿A qué distancia se
encuentra el bote de la base del faro?
d) Un hombre que está situado en un globo suspendido en el aire observa dos
iglesias que están separadas por un kilómetro. Cuando está exactamente
en el punto medio entre ellas mide el ángulo de depresión a una de ellas y
resulta de 45|. Halla la altura del globo.
e) Desde la cima de una colina los ángulos de depresión a dos letreros
indicadores de kilómetros sucesivos de un camino recto son de 45° y 30°
respectivamente. Halla la altura de la colina y la distancia del letrero más
cercano a la base de la colina.
f) Una persona cuyo ojo está a 1,70 metros de altura mide el ángulo de
elevación a la cúspide de un poste telefónico y es de 45°, y el ángulo de
depresión a la base del poste y es de 30°. Hallar la altura del poste y su
distancia con el observador.
g) Desde un bote, se miden los ángulos de elevación a la cúspide y de
depresión a la base del asta de una bandera de 8 metros de altura situada
en el borde de un acantilado resultado 60° y 45° respectivamente. Hallar la
altura del acantilado del mar y la distancia de la base del acantilado al bote.
h) En la construcción de una carretera, para franquear un accidente geográfico
se hará un puente que se sostiene en cuatro pilares, con un ángulo de
elevación de 30°, como se indica en el dibujo. ¿Cuál es la longitud del
puente?
i) Manuel, un astrónomo principiante, midió el ángulo que se muestra en la figura
para calcular la distancia que hay entre los centros de la Luna y la Tierra.
Considerando que el radio de la Tierra es 6380 km, ¿qué resultado obtuvo
Manuel?
j) Determina el ángulo de inclinación mínimo (aproximado al entero)necesario para
que el avión de la figura pueda despegar sobrevolando el cerro.
8
4 21
4
2 10
10
b) tgα =
c) a )
b=
b=
5
5
3
5
5
2 2
2
3
5
3 5
e) senα =
1)d) cos α =
cos ecα =
cos α =
sec α =
3
2
3
5
3
2 5
5
α
2) x = 40 2 3) a) ∠DAC =
e) tgα =
ctgα =
5
2
2
senα
⎛α ⎞
c) tg ⎜ ⎟ =
3) b) CD = senα , OD = cos α
⎝ 2 ⎠ 1 + cos α
ii) tg22,5°= 2 − 1
3) d) i) tg 15° = 2 − 3
4) a) tgα b) secα • cos ecα c) − cos 2 α d) sec 2 α e) 2 cos ecα
f) 2 secα g) − 2ctgα h) 2 secα i) secα • cos ecα j) sec 2 α
k) senα l) − cos 2 α m) senα n) cos α
Respuestas: 1) a) a =
4
3( 3 + 1)
c)
d) 0 e) 1 6) a) 37 3 metros
3
2
6) b) 12 3 kilómetros c) 20 3 metros d) 500 metros
5) a) 0 b)
3 +1
kilómetros
2
f) d = 1,70 3 metros
h= 1,70( 3 + 1) metros
e) h = d =
(
)
500 3
3
i) Aprox. 365.510 Kilómetros j) 22°
g) h = d = 4 3 + 1
metros
h)
metros