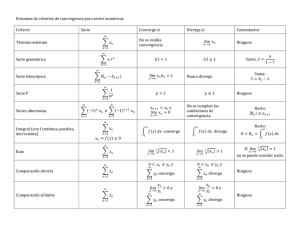
Series de números reales

Tema 6
Series de números reales
6.1
Series de números reales.
∞
Definición 6.1 – Sea {an }∞
n=1 una sucesión de números reales y consideremos la sucesión {Sn }n=1 ,
definida por
Sn = a1 + a2 + · · · + an , para cada n ∈ IN,
que llamaremos sucesión de sumas parciales de la sucesión {an }∞
n=1 .
∞
Al par de sucesiones {{an }∞
n=1 , {Sn }n=1 } se le denomina serie de término general an , y
suele representarse por
∞
P
n=1
6.1.1
an .
Carácter de una serie.
Definición 6.2 – Diremos que la serie
∞
P
n=1
an es convergente, divergente u oscilante, si la
sucesión {Sn }∞
n=1 es respectivamente convergente, divergente u oscilante.
Si la serie converge y Sn −→ S , se dice que S es la suma de la serie y se escribe S =
Series geométricas 6.3 – Las series de la forma
∞
P
∞
P
n=1
an .
an , con a ∈ IR constante, son:
n=1
a) Divergentes, si a ≥ 1
b) Convergentes, si |a| < 1
c) Oscilantes, si a ≤ −1
Demostración:
Consideremos
Sn = a + a2 + · · · + an−1 + an
restando ambas, obtenemos que
¦ Si a 6= 1, tenemos que Sn =
y
(1 − a)Sn = a − an+1
a−an+1
1−a
y, por tanto:
. En cuyo caso
an+1
a−
n→∞ 1 − a
lim Sn = lim
n→∞
aSn = a2 + a3 + · · · + an + an+1


+∞, si a > 1


=
a
1−a , si |a| < 1



6 ∃ , si a ≤ −1
n)
¦ Si a = 1, tenemos que Sn = 1 + 1+ · · · +1 = n y, por tanto, lim Sn = lim n = +∞.
n→∞
n→∞
Definición 6.4 – Diremos que dos series tienen el mismo carácter, y lo representaremos por
“∼”, si son simultáneamente convergentes, divergentes u oscilantes.
Proposición 6.5 – Sea
∞
P
n=1
Sucesiones y Series de Funciones.
an una serie numérica. Se tiene que
75
6 Series de números reales
∞
P
a)
n=1
∞
P
b)
n=1
an ∼
an ∼
∞
P
n=1
λan , para todo λ ∈ IR − {0}.
∞
P
n=k0 +1
an , para todo k0 ∈ IN.
c) Si la serie es convergente (o es divergente), la serie
∞
P
j=1
bj formada de la anterior agru-
pando términos consecutivos, es decir, con bj = anj−1 +1 + anj−1 +2 + · · · + anj , es también
convergente (o es también divergente).
Demostración:
Sea Sn =
n
P
i=1
an , y denotaremos por Sn0 la suma parcial n-ésima de la otra serie involucrada
en cada apartado.
a) Sn0 =
n
n
n
P
P
P
a0n =
λan = λ
an = λSn , luego se tiene que lim Sn0 = λ lim Sn y, por
i=1
i=1
lim S 0
n→∞ n
n→∞
i=1
n→∞
tanto,
es finito, infinito o no existe si respectivamente lim Sn es finito, infinito
n→∞
o no existe, y viceversa.
b) Sea k0 ∈ IN fijo. Para cada n, se tiene
Sn0
kX
0 +n
=
aj =
j=k0 +1
kX
0 +n
j=1
aj −
k0
X
aj = Sk0 +n − Sk0 ,
j=1
luego
lim Sn0 = lim (Sk0 +n − Sk0 ) = −Sk0 + lim Sk0 +n .
n→∞
n→∞
n→∞
lim S 0
n→∞ n
En consecuencia,
es finito, infinito o no existe si respectivamente lim Sn es finito,
n→∞
infinito o no existe, y viceversa.
c) Basta tener en cuenta que
S10 = b1 = a1 + a2 + · · · + an1 = Sn1
S20 = b1 + b2 = a1 + · · · + an1 + an1 +1 + · · · + an2 = Sn2
..
.
Sj0 = b1 + · · · + bj = a1 + · · · + an1 + · · · + anj−1 +1 + · · · + anj = Snj ,
n
es decir, que
Sj0
o∞
n
j=1
= Snj
o∞
j=1
es una subsucesión de {Sn }∞
n=1 . Por tanto, si el lı́mite
de {Sn }∞
n=1 existe y es finito/infinito, el lı́mite de una subsucesión suya existe y toma el
mismo valor finito/infinito.
6.1.2
Series convergentes.
Proposición 6.6 – Sean
∞
P
y
n=1
76
(an + bn ) =
∞
P
n=1
∞
P
an y
n=1
∞
P
an +
n=1
∞
P
n=1
bn dos series convergentes, entonces
∞
P
n=1
(an + bn ) converge
bn .
Sucesiones y Series de Funciones.
6.2 Series de términos positivos.
Demostración:
Sean S = lim Sn = lim
n→∞
n
P
n→∞ i=1
ai y S 0 = lim Sn0 = lim
n
X
Sn00 =
n→∞
(ai + bi ) =
i=1
n
P
n→∞ i=1
n
X
ai +
i=1
n
X
bi . Entonces
bi = Sn + Sn0 ,
i=1
de donde,
lim Sn00 = lim (Sn + Sn0 ) = lim Sn + lim Sn0 = S + S 0
n→∞
y, por tanto,
∞
P
n→∞
(an + bn ) converge y
n=1
n→∞
∞
P
(an + bn ) =
n=1
∞
P
Condición necesaria de convergencia 6.7 – Si
n=1
n→∞
∞
P
n=1
an +
∞
P
n=1
bn .
an es convergente entonces lim an = 0.
n→∞
Demostración:
Como Sn −→ S y Sn = Sn−1 + an , se tiene que an = Sn − Sn−1 y, por tanto,
lim an = lim (Sn − Sn−1 ) = lim Sn − lim Sn−1 = S − S = 0
n→∞
n→∞
n→∞
n→∞
∞
P
1
n , diverge.
La serie armónica 6.8 – La serie armónica,
n=1
Solución:
Verifica la condición necesaria, pues lim
1
n→∞ n
= 0, pero no converge.
Supongamos que sı́ converge, es decir, que lim Sn = S ∈ IR. Entonces, para ε = 14 , existirá
n→∞
1
1
un n0 , tal que si n ≥ n0 se verifica que |S − Sn | = | n+1
+ n+2
+ · · · | < 41 ; pero esto es absurdo
ya que como los términos de la sucesión son positivos se tiene que:
|S−Sn | =
1
1
1
1
1
1
1
1
n
1
1
+
+· · ·+
+· · · >
+
+· · ·+
>
+ +· · ·+
=
=
n+1 n+2
n+n
n+1 n+2
n+n
2n 2n
2n
2n
2
y no puede ser menor que
1
4
si es mayor que
1
2.
En consecuencia,
∞
P
1
n no converge.
n=1
1
Además, como Sn+1 = Sn + n+1
, la sucesión {Sn }∞
n=1 es monótona creciente y no converge,
luego no está acotada superiomente, es decir, Sn −→ +∞ y la serie diverge.
4
6.2
Series de términos positivos.
Diremos que una serie
∞
P
n=1
an es de términos positivos si an ≥ 0, para todo n ∈ IN.
Teorema 6.9 – Una serie de términos positivos
parciales {Sn }∞
n=1 está acotada superiormente.
∞
P
n=1
an converge si, y sólo si, la sucesión de sumas
Demostración:
Como an ≥ 0 se tiene que Sn = Sn−1 + an ≥ Sn−1 , luego la sucesión de sumas parciales
{Sn }∞
n=1 es monótona creciente.
Entonces,
Sucesiones y Series de Funciones.
77
6 Series de números reales
⇐=c si {Sn }∞
n=1 está acotada superiormente, por ser monótona creciente, es convergente, luego
∞
P
n=1
an converge;
=⇒c si {Sn }∞
n=1 no está acotada, por ser monótona creciente, se tiene que Sn −→ +∞ luego
∞
P
n=1
an diverge a +∞ y, por tanto, no converge.
Observación 6.10 – El resultado anterior (ası́ como los resultados siguientes sobre series de
términos positivos) son ciertos también para series que sólo sean de términos positivos a partir
de un término en adelante, es decir, que exista n0 ∈ IN tal que an ≥ 0, para todo n ≥ n0 . Para
∞
P
verificarlo, basta tener en cuenta que
∞
P
Además, como
∞
P
an ∼
n=1
∞
P
carácter de una serie
n=1
n=1
an ∼
∞
P
n=n0
an (apartado (b) de la proposición 6.5).
(−1)an (apartado (a) de la proposición 6.5), para estudiar el
n=1
an de términos negativos o negativos a partir de un término en adelante,
basta estudiar el carácter de la serie de términos positivos
∞
P
(−1)an .
n=1
6.2.1
Criterios de comparación.
∞
P
Primer criterio de comparación 6.11 – Sean
n=1
an y
∞
P
n=1
bn series de términos positivos tales
que an ≤ bn , para todo n ∈ IN —o a partir de un término en adelante—, entonces:
a) Si
∞
P
n=1
b) Si
∞
P
n=1
bn converge =⇒
an diverge =⇒
∞
P
n=1
∞
P
n=1
bn diverge.
Demostración:
Como an ≤ bn , se tiene Sn =
a) Si
∞
P
n=1
∞
P
n=1
∞
P
n=1
n
P
j=1
an ≤
n
P
j=1
bn = Sn0 y, entonces,
∞
bn converge =⇒ {S 0 n }∞
n=1 está acotada superiormente =⇒ {Sn }n=1 está acotada
superiormente =⇒
b) Si
an converge.
an converge.
0 ∞
an diverge =⇒ {Sn }∞
n=1 no está acotada superiormente =⇒ {S n }n=1 no está
acotada superiormente =⇒
∞
P
n=1
bn diverge.
Ejemplo.- Estudiar el carácter de las series
∞
P
n=1
1
n+3n
y
∞
P
n=1
1
3n−7 .
Solución:
La primera es de términos positivos pues n + 3n > 0 para todo n. Además n + 3n ≥ 3n ,
para todo n, luego se tiene que
también la serie
∞
P
n=1
1
n+3n
1
n+3n
≤
1
3n
, para todo n. Entonces, como
∞
P
1
3n converge,
n=1
converge.
Para la segunda, 3n − 7 > 0 para n ≥ 3, luego es de términos positivos a partir de n0 = 3
1
1
y 3n − 7 < 3n, para todo n ≥ 3, luego se tiene que 3n−7
> 3n
, para todo n ≥ 3. Entonces,
78
Sucesiones y Series de Funciones.
6.2 Series de términos positivos.
como
∞
P
n=1
∞
∞
∞
∞
P
P
P
P
1 1
1
1
1
3n =
3 · n ∼
n y esta diverge, la serie
3n−7 diverge y, por tanto, la serie
n=3
n=3
1
3n−7 diverge.
n=3
n=3
4
∞
P
Segundo criterio de comparación 6.12 – Sean
an
n→∞ bn
que lim
n=1
= L, entonces:
a) Si 0 < L < +∞ =⇒
∞
P
n=1
b) Si L = 0 y
∞
P
(i)
n=1
∞
P
(ii)
n=1
an ∼
∞
P
n=1
an y
∞
P
n=1
bn series de términos positivos tales
bn
bn converge =⇒
an diverge =⇒
∞
P
n=1
∞
P
n=1
an converge.
bn diverge.
Demostración:
a) Si 0 < L < +∞, y tomamos ε =
| abnn − L| < L2 . De donde
L
2,
existe n0 ∈ IN tal que si n ≥ n0 se tiene que
− L2 + L <
an
<
bn
L
2
+L
y, como bn ≥ 0, se tiene
0≤
L
2 bn
≤ an ≤
3L
2 bn
para todo n ≥ n0 . Aplicando el Primer criterio de comparación a los casos 0 ≤
y 0 ≤ an ≤ 3L
2 bn se obtiene el resultado.
L
2 bn
≤ an
b) Si L = 0, tomando ε = 1, se tiene que existe n0 ∈ IN tal que si n ≥ n0 entonces
0 ≤ an < bn , y recaemos en el Primer criterio.
Observación 6.13 – Si L = +∞, también puede aplicarse el criterio intercambiando los papeles
de an y bn , pues entonces se tiene que lim abnn = 0.
n→∞
Ejemplo.- Estudiar el carácter de la serie de términos positivos
Solución:
∞
P
√1 .
n
n=1
1
n
n→∞ √1
n
Como lim
√
n
n→∞ n
= lim
= 0, y
∞
∞
P
P
1
√1 diverge.
diverge,
se
tiene
que
n
n
n=1
n=1
4
Criterio de la integral 6.14 – Sea f : [1, +∞) −→ IR positiva, monótona decreciente e integrable
en cada cerrado [1, n], y sean an = f (n). Entonces
∞
X
n=1
an converge ⇐⇒ bn =
Z n+1
1
f (x) dx converge.
Demostración:
Por ser f monótona decreciente, en cada intervalo [m, m + 1], se verifica que
am = f (m) ≥ f (x) ≥ f (m + 1) = am+1 ,
Sucesiones y Series de Funciones.
79
6 Series de números reales
a1
a2
a3
a4
a5
1
2
4
3
5
Fig. 6.1.
y, por tanto, que
am =
Z m+1
m
am dx ≥
Z m+1
m
f (x) dx ≥
Z m+1
m
am+1 dx = am+1 .
Luego,
a1 + a2 + · · · + an ≥
es decir, Sn ≥
Z n+1
1
Z 2
1
f (x) dx +
Z 3
2
f (x) dx + · · · +
Z n+1
n
f (x) dx > a2 + a3 + · · · + an+1
f (x) dx = bn ≥ Sn+1 − a1 . Como las tres sucesiones son de términos
positivos, basta aplicar adecuadamente el primer citeriode comparación:
⇐=c si bn converge, entonces Sn+1 − a1 converge y por tanto
=⇒c si bn diverge, entonces Sn diverge y por tanto
Ejemplo 6.15 – Estudiar el carácter de las series
Solución:
Si α > 0: n1α = f (n) para la función f (x) =
[1, +∞). Como
bn =
Z n+1
1
1
x
dx =
α
1
1−α
µ
∞
P
n=1
∞
P
n=1
an converge.
an diverge.
∞
P
1
nα , según los valores de α > 0.
n=1
1
xα
, función que es positiva y decreciente en
¶
1
−1 , si α 6= 1,
(n+1)α−1
y
bn =
Z n+1
1
1
x
dx = ln(n + 1), si α = 1,
se tiene que bn converge si α > 1 y diverge si α ≤ 1.
En consecuencia,
∞
P
1
nα converge si α > 1 y diverge si α ≤ 1.
n=1
6.2.2
4
Criterios de convergencia.
Los criterios de comparación de la subsección anterior son también criterios para el estudio de la
convergencia, pero que necesitan de otra serie con la que comparar. Los criterios de esta nueva
subsección, sólo usan los propios términos de la serie para obtener los resultados.
Criterio del cociente (o de D‘Alambert) 6.16 – Sea
an+1
que
lim
= L. Entonces:
n→∞ an
80
∞
P
n=1
an una serie de términos positivos tal
Sucesiones y Series de Funciones.
6.2 Series de términos positivos.
a) si L < 1 =⇒
∞
P
n=1
b) si L > 1 =⇒
∞
P
n=1
an converge.
an diverge.
c) si L = 1 el criterio no decide.
Demostración:
a) Si L < 1, tomemos k = L + ε > 0 tal que L < k < 1, entonces debe existir n0 ∈ IN tal
que para todo n ≥ n0 se verifica que an+1
an ≤ k < 1 y, por tanto, que an+1 ≤ kan , para
todo n ≥ n0 . Luego
an0 +1 ≤ kan0
an0 +2 ≤ kan0 +1 ≤ k 2 an0
an0 +3 ≤ kan0 +2 ≤ k 3 an0
an0 +4 ≤ kan0 +3 ≤ k 4 an0
..
..
.
.
an = an0 +(n−n0 ) ≤ kan−1 ≤ k n−n0 an0
..
..
.
.
Sumando miembro a miembro, se obtiene
∞
X
n=n0 +1
∞
P
de donde
n=n0 +1
∞
X
an ≤
n=n0 +1
an+1
an
kn ,
n=n0 +1
an converge, ya que la serie geométrica
b) Si L > 1, entonces ∃n0 ∈ IN tal que
∞
X
k n−n0 an0 = an0 k −n0
∞
P
k n converge (|k| = k < 1).
n=n0 +1
> 1, para todo n ≥ n0 , luego
an < an+1 , para todo n ≥ n0 ,
y la serie diverge ya que an 6→ 0.
Nota: Si el criterio no decide, es decir, que si para una serie L = 1 ésta puede ser tanto
convergente como divergente. Puede verse considerando las series
∞
P
1
que es convergente, pues en ambas L = 1.
n2
∞
P
1
n que es divergente y
n=1
n=1
Ejemplo.- Estudiar el carácter de la serie
∞
P
1
n! .
n=1
Solución:
Como
an+1
= lim
n→∞ an
n→∞
lim
1
(n+1)!
1
n!
= lim
n→∞
n!
1
= lim
= 0 < 1,
(n + 1)! n→∞ n + 1
la serie converge.
Criterio de Raabe 6.17 – Sea
Entonces:
Sucesiones y Series de Funciones.
4
∞
P
n=1
³
an una serie de términos positivos con lim n 1 −
n→∞
an+1
an
´
= R.
81
6 Series de números reales
a) si R > 1 =⇒
∞
P
an converge.
n=1
b) si R < 1 =⇒
∞
P
an diverge.
n=1
c) si R = 1 el criterio no decide.
Ejemplo.- Estudiar el carácter de la serie
∞
P
1
.
n2
n=1
Solución:
1/(n+1)2
an+1
n2
n2
Como an+1
= (n+1)
= lim (n+1)
2 y lim
2 = 1, el criterio del cociente no
an =
1/n2
n→∞ an
n→∞
decide. Aplicando Raabe, tenemos que
µ
an+1
lim n 1 −
n→∞
an
¶
Ã
n2
= lim n 1 −
n→∞
(n + 1)2
!
= lim n
n→∞
2n + 1
(n + 1)2 − n2
= lim n
n→∞ (n + 1)2
(n + 1)2
2n2 + n
2n2 + n
=
lim
= 2 > 1,
n→∞ (n + 1)2
n→∞ n2 + 2n + 1
= lim
y la serie converge.
4
Criterio de la raı́z (o de Cauchy) 6.18 – Sea
√
lim n an = L. Entonces:
∞
P
n=1
an una serie de términos positivos tal que
n→∞
a) si L < 1 =⇒
∞
P
n=1
b) si L > 1 =⇒
∞
P
n=1
an converge.
an diverge.
c) si L = 1 el criterio no decide.
Demostración:
a) si L < 1, tomemos k > 0 tal que L < k < 1, entonces existe n0 ∈ IN tal que para todo
∞
∞
P
P
√
n ≥ n0 , se verifica que n an ≤ k y por tanto, que an ≤ k n , de donde
an ≤
kn y
∞
P
n=n0
n=n0
an converge ya que está mayorada que una serie que converge.
b) si L > 1, entonces existe n0 ∈ IN tal que para todo n ≥ n0 , se verifica que
luego an > 1 y la serie no puede converger ya que an 6→ 0.
Ejemplo.- Estudiar el carácter de la serie
Solución:
Converge, pues:
82
n=n0
√
n a
n > 1,
∞
P
n
2n .
n=1
lim
n→∞
q
√
n a = lim n n = lim
n
2n
n→∞
√
nn
√
n n
2
n→∞
√
nn
n→∞ 2
= lim
=
1
2
< 1.
4
Sucesiones y Series de Funciones.
6.3 Series de términos cualesquiera.
6.3
Series de términos cualesquiera.
6.3.1
Convergencia absoluta.
Definición 6.19 – Una serie
∞
P
n=1
∞
P
n=1
an se dice absolutamente convergente si, y sólo si, la serie
|an | es convergente.
Teorema 6.20 – Toda serie absolutamente convergente es convergente.
Demostración:
∞
P
Si
n=1
¯
que
|an | converge, entonces, para cada ε > 0, existe n0 ∈ IN tal que si n ≥ n0 , se verifica
¯
¯
¯
¯|an | + |an+1 | + · · · + |an+p |¯ < ε, para todo p ∈ IN. Pero, como
¯
¯
¯
¯
|an + an+1 + · · · + ap+n | ≤ |an | + |an+1 | + · · · + |an+p | = ¯|an | + |an+1 | + · · · + |an+p |¯ < ε
la serie
∞
P
n=1
an también converge.
Ejemplo 6.21 – Estudiar el caracter de la serie
∞
P
sen n
.
n2
n=1
Solución:
Como la serie no es de términos positivos (ni negativos), no podemos aplicar los criterios de
la sección anterior. Veamos si converge absolutamente, es decir, estudiemos la serie de términos
¯
∞
∞ ¯
P
P
¯ sen(n) ¯
| sen(n)|
1
< n12 y como
converge, también converge
¯ n2 ¯ . Tenemos que
n2
n2
n=1
n=1
∞
∞
P
P
| sen(n)|
sen n
positivos
n2
n=1
6.3.2
y, en consecuencia,
n=1
n2
converge.
4
Series de Leibnitz.
Teorema de Leibnitz 6.22 – Sea {an }∞
n=1 una sucesión de términos positivos, monótona decre∞
P
ciente y de lı́mite cero. Entonces la serie
(−1)n+1 an converge.
n=1
Demostración:
∞
∞
Para demostrarlo, veamos que {Sn }∞
n=1 = {S2n−1 }n=1 ∪ {S2n }n=1 converge, probando que
∞
∞
{S2n−1 }n=1 y {S2n }n=1 convergen al mismo valor.
En efecto, los términos S2(n+1) y S2(n+1)−1 , par e impar, de la sucesión de sumas parciales
se obtienen de los anteriores términos par e impar con
S2n+2 = S2n + (−1)2n+2 a2n+1 + (−1)2n+3 a2n+2 = S2n + a2n+1 − a2n+2 = S2n + (a2n+1 − a2n+2 )
S2n+1 = S2n−1 + (−1)2n+1 a2n + (−1)2n+2 a2n+1 = S2n−1 − a2n + a2n+1 = S2n−1 − (a2n − a2n+1 )
Como {an }∞
n=1 es decreciente, ak − ak+1 ≥ 0 para todo k , entonces
S2n+2 ≥ S2n ,
luego
{S2n }∞
n=1
es creciente y
y
S2n+1 ≤ S2n−1 ,
{S2n−1 }∞
n=1
S2 ≤ S4 ≤ · · · ≤ S2n ≤ S2n+2 ≤ · · ·
para todo n ≥ 1;
es decreciente, y se tiene
y
· · · ≤ S2n+1 ≤ S2n−1 ≤ · · · ≤ S3 ≤ S1
h6.1i
Además, como
S2n = S2n−1 + (−1)2n+1 an = S2n−1 − a2n ≤ S2n−1 ,
Sucesiones y Series de Funciones.
83
6 Series de números reales
de h6.1i se tiene que
S2 ≤ S2n ≤ S2n−1 ≤ S1
∞
y, en consecuencia, {S2n }∞
n=1 está acotada superiormente por S1 y {S2n−1 }n=1 está acotada
inferiormente por S2 , luego convergen.
Concluyendo, como existe el lim S2n , existe el lim S2n−1 , lim an = 0 y S2n = S2n−1 −a2n ,
n→∞
n→∞
n→∞
se tiene que
0 = lim a2n = lim (S2n−1 − S2n ) = lim S2n−1 − lim S2n ;
n→∞
n→∞
luego lim S2n−1 = lim S2n y
n→∞
n→∞
Definición 6.23 – Una serie
n→∞
{Sn }∞
n=1
∞
P
n=1
n→∞
converge.
an , se dice que es que es alternada si el signo de an es distinto
del signo de an+1 , para todo n.
Una serie
∞
P
n=1
an , se dice que es que es Leibnitz si es alternada y verifica las condiciones del
teorema
de Leibnitz.
Es decir, si es alternada, verifica la condición necesaria de convergencia
³
´
lim an = 0 y la sucesión {|an |}∞
n=1 es decreciente.
n→∞
Ejemplo.- La serie armónica alternada,
∞
P
(−1)n+1
n=1
n
es convergente.
Solución:
¯
¯
n+1 ¯
¯
1
Es una serie alternada, lim ¯ (−1)n ¯ = lim n1 = 0 y n1 > n+1
, luego es una serie de
n→∞
n→∞
Leibnitz y, en consecuencia, converge. (De hecho, la suma de esta serie es ln 2.)
4
Corolario 6.24 – Si
∞
P
n=1
an es una serie de Leibnitz, entonces |S − Sn | ≤ |an+1 |, para todo n.
Demostración:
Supongamos, sin pérdida de generalidad que a1 > 0, a2 < 0, a3 > 0, a4 < 0, . . . , es decir,
que
∞
P
n=1
an =
∞
P
(−1)n+1 |an |. Por la demostración del teorema de Leibnitz, se cumple
n=1
S2 ≤ S4 ≤ · · · ≤ S2n ≤ S2n+2 ≤ · · · ≤ S ≤ · · · ≤ S2n+1 ≤ S2n−1 ≤ · · · ≤ S3 ≤ S1 ,
luego:
¦ Si n es par, n + 1 es impar y Sn ≤ S ≤ Sn+1 . Restando Sn en cada parte, se tiene
0 ≤ S − Sn ≤ Sn+1 − Sn = an+1 = |an+1 |.
¦ Si n es impar, n + 1 es par y Sn+1 ≤ S ≤ Sn . Restando Sn en cada parte, se tiene
Sn+1 − Sn ≤ S − Sn ≤ 0 y, como Sn+1 − Sn = an+1 = −|an+1 |, queda
−|an+1 | ≤ S − Sn ≤ 0.
En consecuencia,
|S − Sn | ≤ |an+1 |, para todo n.
Nota: Como en el caso de las series de términos positivos, todos los resultados anteriores son
aplicables a series que verifiquen las condiciones a partir de un término en adelante.
84
Sucesiones y Series de Funciones.
6.4 Ejercicios
6.3.3
Multiplicación de series.
Teorema 6.25 – Sean
∞
P
n=1
∞
P
an y
convergente, entonces la serie
∞
X
n=1
cn =
∞
X
à n
X
n=1
i=1
bn series convergentes y al menos una de ellas absolutamente
n=1
!
=
ai bn−i+1
∞
X
(a1 bn + a2 bn−1 + · · · + ai bn−i+1 + · · · + an b1 )
n=1
∞
P
obtenida como producto de Cauchy de las series
n=1
∞
X
cn =
̰
X
n=1
6.4
an y
! ̰
X
an ·
n=1
∞
P
n=1
bn converge, y se verifica que
!
bn .
n=1
Ejercicios
6.1 Usar la condición necesaria de convergencia y los criterios de comparación, para estudiar
el carácter de las siguientes series
∞
P
a)
√ 1 2
n− 3
n=1
∞
P
c)
√
3e−
n=1
n2 +1
1
3−cos
1
n
∞
P
n+1
1
n+1
n tg n ln n
d)
n=1
n=1
√
∞ √ 2
P
n +n+1− n2 −n+1
e)
∞
P
b)
n
n=1
∞ ³
P
f)
1+
n=1
1
n
´n2
e−n
6.2 Estudiar el carácter de las siguientes series
a)
c)
1
1·2·3
∞
P
n=1
e)
∞
P
n=2
g)
∞
P
1
2·3·4
+
1
3·4·5
+ ···
b)
∞ n
P
e
n=0
n!
3·5·7···(2n+1)
d)
1
n ln n
f)
1
(−1)n−1 tg n√
n
n=1
Sucesiones y Series de Funciones.
+
µ³
∞
P
n=1
∞
P
n!
n+1
n
´n+1
−
n+1
n
¶−n
(−1)n lnnn
n=1
h)
√
∞
P
1+(−1)n n
n=1
n+1
85
6 Series de números reales
6.3 Estudiar el carácter de las siguientes series, según los valores de los parámetros.
∞ 2n+1
P
x
a)
2n−1
n=1
∞
P
n=1
(−1)n+1 nln1 α , α > 0
∞
P
g)
tgn a +
n=1
∞
P
i)
θ
n
´
³
´β
∞
P
h)
1
a∈
/ ZZ−
1
a(1+ 2 +···+ n ) , a > 0, a 6= e−1
³
´β
1
(−1)n+1 nα e n − 1
n=1
, 0<α<β
∞
P
j)
n=2
6.4 Usar la serie
n!
(a+1)(a+2)···(a+n) ,
n=1
, 0 < a < π2
(−1)n nα ln n+1
n−1
∞
P
f)
n=1
³
∞
P
d)
n=1
e)
n
n=1
´
´
³
³
∞
P
1
k
k
(1
−
k)
1
−
·
·
·
1
−
n
2
n
c)
∞
n
P
(a+1)
√
b)
n=1
2
αn +α−n ,
α 6= 0
∞ n
P
n
x
lim xn! , en cada x ∈ IR.
n! para encontrar el n→∞
n=0
6.5 Estúdiese, según los valores de x ∈ IR, el carácter de las series
a)
∞
P
(x2 −1)n
n=0
b)
2n+1
6.6 Dada la serie
∞
P
(x2 −4)n
n=0
n+1
c)
³
´n
∞
P
1 x+2
n=1
n
1−x
d)
³ 2 ´n+1
∞
P
(−1)n
2x
n=0
2n
2−3x
x
, se pide:
2 n
n=0 (1 + x )
∞
P
a) ¿Para qué valores de x ∈ IR la serie converge?
b) Hallar la suma de la serie en los x donde converja.
6.7 Sean
∞
P
n=1
an y
∞
P
n=1
bn dos series de términos positivos convergentes.
a) Demostrar que
b) Demostrar que
∞
P
n=1
∞
P
n=1
a2n converge.
an bn converge.
c) Encontrar una serie de términos positivos convergente para la que la serie
sea convergente y otra para la que sea divergente.
d) ¿Qué se puede decir sobre el carácter de la serie
∞ √
P
n=1
an
∞
P
an
bn ?
n=1
86
Sucesiones y Series de Funciones.