Práctica 4 Métodos de resolución numérica de ecuaciones

practica6.nb
1
Práctica 4
Métodos de resolución numérica de
ecuaciones
El objetivo de esta práctica es resolver una ecuación del tipo f(x)=0 aplicando un método numérico. Cuando
queramos emplear algún método numérico para aproximar una posible raíz de una ecuación, lo primero que
tenemos que estudiar es si dicha ecuación puede tener soluciones reales y comprobar que se dan las condiciones
necesarias para poder aplicar el método correspondiente.
Siempre será muy interesante expresar la ecuación de la forma f(x) = 0 y representar gráficamente la función f(x)
en un intervalo apropiado.
De esta manera, la ecuación tendrá una interpretación geométrica clara, y nos guiará en la búsqueda de los puntos
de corte de la gráfica de dicha función con el eje OX.
Los métodos que vamos a estudiar generan una sucesión {xn }, nœN, de valores aproximados de la solución.
El método se dice que es convergente si se cumple limnض xn = s, donde s es la solución de la ecuación f(x) = 0.
El error cometido en la n-sima aproximación viene dado por en = » xn - s ».
En algunos métodos numéricos (bisección y punto fijo) se dispone de una cota del error de aproximación.
Si no se dispone de una cota del error de aproximación puede tomarse la cantidad en =
»xn - xn-1 »
.
»xn »
Existencia de solución (Teorema de Bolzano)
Si f es una función continua en [a, b] y f(a) f(b) < 0, entonces existe al menos un s œ (a, b) tal que f(s) = 0.
Unicidad de solución (Corolario del Teorema de Rolle)
Si f' '(x) ∫ 0 para todo x œ (a,b), entonces f se anula a lo sumo una vez en el intervalo [a,b]
1. Método de la Bisección.
Sea f:AØR una función continua en A y supongamos que hemos localizado un intervalo [a,b] en el que tiene una
única raiz.
El método de bisección genera una sucesión de intervalos encajados y en cada iteración la aproximación xn de la
raiz de f(x) = 0 es el punto medio del intervalo,
y viene dada por xn =
an + bn
.
2
Una cota del error cometido en la n-sima iteración viene dada por en = »xn - s … §
b-a
2n+1
Ejemplo 1.1 Aplicar el método de bisección con 10 iteraciones para obtener una
solución aproximada de la ecuación 2 x - sen x - 1 = 0 y dar una cota del error
cometido.
à Definimos la función
f@x_D := 2 x − Sin@xD − 1
practica6.nb
2
Buscamos un intervalo donde haya alternancia de signo
f@0D
−1
f@1D êê N
0.158529
Luego existe solución en el intervalo [0,1].
à Unicidad de la solución
f '@xD
2 − Cos@xD
Al ser la derivada distinta de cero para todo x œ R, la solución es única.
à Aplicamos el algoritmo de la bisección
a0 = 0; b0 = 1; niter = 10;
ForBn = 0, n ≤ niter, n ++,
xn =
an + bn
;
2
If@f@xn D 0, Print@"Solución exacta", xn D; Break@DD;
If@f@xn D f@an D < 0, an+1 = an ; bn+1 = xn , an+1 = xn ; bn+1 = bn DF;
PrintB"Solución aproximada = ", N@xniter , 10D,
" con error menor que " , NB
b0 − a0
, 2FF
2niter+1
Solución aproximada = 0.8881835938 con error menor que 0.00049
Podemos presentar los resultados de todas las iteraciones de la siguiente forma (activando previamente en el menú
CellØDefault Output Format TypeØTraditionalForm):
practica6.nb
3
a0 = 0; b0 = 1;
A = Array@B, 812, 7<, 80, 0<D;
B@0, 0D = "n"; B@0, 1D = "an "; B@0, 2D = "bn "; B@0, 3D = "xn ";
B@0, 4D = "fHan L"; B@0, 5D = "fHbn L"; B@0, 6D = "fHxn L";
ForBn = 0, n ≤ 10, n ++,
xn =
an + bn
;
2
B@n + 1, 0D = n; B@n + 1, 1D = N@an , 10D; B@n + 1, 2D = N@bn , 10D;
B@n + 1, 3D = N@xn , 17D; B@n + 1, 4D = N@f@an DD;
B@n + 1, 5D = N@f@bn DD; B@n + 1, 6D = N@f@xn DD;
If@f@xn D f@an D < 0, an+1 = an ; bn+1 = xn , an+1 = xn ; bn+1 = bn DF;
A
Print@"Solución aproximada = ", N@x10 , 20DD;
Print@"Error ≤ ", N@Hb0 − a0 L ê 2 ^ 11DD
88n, an , bn , xn , fHan L, fHbn L, fHxn L<,
80, 0, 1.000000000, 0.50000000000000000, −1., 0.158529, −0.479426<,
81, 0.5000000000, 1.000000000, 0.75000000000000000, −0.479426,
0.158529, −0.181639<, 82, 0.7500000000, 1.000000000,
0.87500000000000000, −0.181639, 0.158529, −0.0175435<,
83, 0.8750000000, 1.000000000, 0.93750000000000000, −0.0175435,
0.158529, 0.0689189<, 84, 0.8750000000, 0.9375000000,
0.90625000000000000, −0.0175435, 0.0689189, 0.0253034<,
85, 0.8750000000, 0.9062500000, 0.89062500000000000, −0.0175435,
0.0253034, 0.00378502<, 86, 0.8750000000, 0.8906250000,
0.88281250000000000, −0.0175435, 0.00378502, −0.00690282<,
87, 0.8828125000, 0.8906250000, 0.88671875000000000, −0.00690282,
0.00378502, −0.00156481<, 88, 0.8867187500, 0.8906250000,
0.88867187500000000, −0.00156481, 0.00378502, 0.00110863<,
89, 0.8867187500, 0.8886718750, 0.88769531250000000, −0.00156481,
0.00110863, −0.000228462<, 810, 0.8876953125, 0.8886718750,
0.88818359375000000, −0.000228462, 0.00110863, 0.000439989<<
Solución aproximada = 0.88818359375000000000
Error ≤ 0.000488281
Ejemplo 1.2 Aplicar el método de bisección para obtener una solución
aproximada de la ecuación 1+ cos x - x = 0 con una precisión de 5 cifras decimales
exactas.
En primer lugar observemos que si x es una solución de la ecuación x = 1 - cos x, x œ [0, 2], es decir fuera del
intervalo no hay soluciones de la ecuación.
practica6.nb
4
Definimos la función
f@x_D := 1 + Cos @xD − x
à Buscamos un intervalo donde haya alternancia de signo
f@0D
2
f@2D êê N
−1.41615
Luego existe solución en el intervalo [0,2].
à Unicidad de la solución
f '@xD
−1 − Sin@xD
Al ser la derivada distinta de cero para todo x œ [0,2], la solución es única en dicho intervalo y, por tanto, en todo
R (por la observación anterior).
Plot@8f '@xD, 0<, 8x, 0, 2<D
0.5
−0.5
−1.0
−1.5
−2.0
1.0
1.5
2.0
practica6.nb
5
Aplicamos el algoritmo de la bisección: como en este caso no conocemos el número de iteraciones que
hemos de realizar, por lo que utilizaremos una instrucción que nos permita interrumpir el algoritmo
cuando hayamos alcanzado la precisión deseada.
Si el número de cifras decimales exactas que queremos conseguir es ncifras, entonces el error debe ser
menor que 12 10−ncifras .
a0 = 0; b0 = 2; ncifras = 5; ε =
WhileBTrue, xn =
an + bn
1
2
10−ncifras ; n = 0;
;
2
b0 − a0
< ε, Print@" Solución aproximada ", N@xn , 10D,
2n+1
" con una precisión de ", ncifras, " decimales."
IfB
"Se han necesitado ", n, " iteraciones"D; Break@DF;
If@f@xn D 0, Print@" Solución exacta ", xn D; Break@DD;
If@f@xn D f@an D < 0, an+1 = an ; bn+1 = xn , an+1 = xn ; bn+1 = bn D; n = n + 1F;
Solución aproximada 1.283428192 con una precisión de
5 decimales. Se han necesitado 18 iteraciones
2. Método de la cuerda o Regula-Falsi
Este método sigue el mismo esquema que el método de la bisección salvo que en cada iteración la aproximación xn
viene dada por xn = an + f(an )
bn - an
f Hbn L - f Han L
En este método no disponemos de una cota del error cometido en la n-sima iteración, por lo que para estimarlo
utilizaremos el valor en =
»xn -xn-1 »
.
»xn »
Ejemplo 2.1 Aplicar el método de la cuerda con 5 iteraciones para resolver la
ecuación 2 x - sen x -1 = 0. Dar una cota del error cometido.
à Definimos la función
f@x_D := 2 x − Sin@xD − 1
practica6.nb
6
Buscamos un intervalo donde haya alternancia de signo (se ha visto en ejemplo 1.)
f@0D
−1
f@1D êê N
0.158529
Presentamos los resultados de todas las iteraciones:
a0 = 0; b0 = 1; niter = 5;
ForBn = 0, n ≤ niter, n ++,
xn = an − f@an D
bn − an
;
f@bn D − f@an D
If@f@xn D 0, Print@"Solución exacta", xn D; Break@DD;
If@f@xn D f@an D < 0, an+1 = an ; bn+1 = xn , an+1 = xn ; bn+1 = bn DF;
PrintB"Solución aproximada = ", N@xniter , 10D,
" con error menor que " , NBAbsB
xniter − xniter−1
xniter
F, 2FF
Solución aproximada = 0.8878622108 con error menor que 2.7 × 10−8
3. Método del Punto Fijo
Un punto fijo de una función F es un valor x tal que F(x) = x. El problema de encontrar las soluciones de una
ecuación f(x)=0 y el de encontrar los puntos fijos de una función F(x) son equivalentes en el siguiente sentido:
Definiendo F(x)=x-f(x), o F(x) = x + f(x), un punto fijo de F será una raíz de f, o , al contrario, una raíz de f será
un punto fijo de F.
Condiciones de convergencia del método de punto fijo. Las condiciones suficientes para la existencia de punto
fijo de F:[a,b]ØR son las siguientes:
i) FœC1 @a, bD
ii) F(x)œ[a,b], "xœ[a,b]
iii) »F' (x)»§k<1, "xœ[a,b]
en cuyo caso existe una única solución de la ecuación F(x) = x en [a,b]. Además, la sucesión {xn }dada por xn+1 =
F(xn ), n = 0,1,2.... converge a dicha solución, siendo x0 un punto arbitrario del intervalo [a,b].
Acotación del error: en la n-sima iteración viene dado por: en = … xn - s … §
Kn
1-K
» x1 - x0 »
practica6.nb
7
Ejemplo 3.1 Aplicar el método de punto fijo para resolver la ecuación 2 x - sen x 1 = 0 con 20 iteraciones. Dar una cota del error cometido.
En ejemplos anteriores hamos probado que la ecuación tiene solución única en el intervalo [0,
1].
1
Hacemos FHxL = 2 H1 + senHxLL
† Definimos la función F(x)
Φ@x_D :=
1
2
H1 + Sin@xDL
† Comprobamos si se cumplen las condiciones suficientes de convergencia:
i) La función FœC1 @0, 1D
Φ'[x]
Cos@xD
2
ii) F(x)œ[0,1], "xœ[0,1]
Podemos comprobarlo representando la gráfica de la función en el intervalo [0,1] y viendo que su imagen queda
dentro del intervalo [0,1].
Plot[{Φ[x],0,1},{x,0,1}]
1.0
0.8
0.6
0.4
0.2
0.2
0.4
0.6
0.8
1.0
practica6.nb
8
iii) »F' (x)»§k<1, "xœ[0,1]
Representamos la gráfica de »F'(x) » en el intervalo [0,1] y tomamos como K el valor máximo en dicho intervalo
(existe por el teorema de Weierstrass)
Plot[{Abs[Φ'[x]],0,1},{x,0,1}]
1.0
0.8
0.6
0.4
0.2
0.2
0.4
0.6
0.8
1.0
Luego podemos tomar K=1/2.
Como se cumplen las tres condiciones, la sucesión dada por xn+1 =F(xn ), n¥0, converge a la solución de la ecuación
partiendo de cualquier punto x0 del intervalo [0,1].
† Aplicamos el método con 20 iteraciones:
K=
1
; x0 = 1;
2
For@n = 0, n ≤ 19, n ++, xn+1 = Φ@xn DD;
Print@"Solución aproximada = ", N@x20 , 10DD;
PrintB"Error de aproximación = ", NB
Solución aproximada = 0.8878622116
Error de aproximación = 1.5 × 10−7
Kn
1−K
Abs@x1 − x0 D, 2FF
practica6.nb
ü
9
Instrucción FixedPoint
Mathematica dispone de la instrucción FixedPoint que implementa directamente este método de aproximación al
punto fijo de una función, el formato básico es
FixedPoint[función iteradora, valor inicial]
Si utilizamos la instrución FixedPoint se implementa directamente este método de aproximación al punto fijo de la
función F.
FixedPoint@Φ, 1., 20D
0.887862
4. Método de Newton-Raphson (o de las
tangentes).
El método de Newton-Rapshon parte de un valor inicial x0 y también ahora se construye iterativamente una
sucesión de valores xk . Para ello utiliza las rectas tangentes a la gráfica de la función en los puntos ( xk , f Hxk ))
calculando el punto de corte de éstas con el eje OX , de esta forma se aproxima la raíz buscada. Para que este
método funcione correctamente será necesario que la derivada de la función no esté próxima a cero, al menos en
cierto entorno de la raíz, ya que de lo contrario se podría producir una división entre cero o bien la creación de
enormes errores de redondeo al dividir entre cantidades muy pequeñas.
Las condiciones suficientes para la convergencia del método de Newton-Raphson son las siguientes: Sea
f:[a,b]ØR fœC2 [a,b]. Si se cumple:
i) f(a) f(b) <0
ii) f' (x) ∫ 0, "xœ[a,b]
iii) f''(x) no cambia de signo en todo el intervalo,
entonces, si partimos de cualquier punto inicial x0 œ[a,b] con la condición de que f(x0 ) f'' (x0 ) > 0, la sucesión
{xn }dada por
xn+1 = xn -
f Hxn L
,
f ' Hxn L
n = 0, 1, 2...
converge a la solución de la ecuación f(x) = 0.
Acotación del error: No se dispone de cota del error cometido en la n-sima iteración, por lo que utilizamos el
valor en =
»xn -xn-1 »
.
»xn »
Ejemplo 4.1 Aplicar el método de Newton-Raphson para resolver la ecuación
x3 + 4 x - 10 = 0 con 5 iteraciones y estimar el error cometido.
† Definimos la función
practica6.nb
10
f[x_]:=x^3 + 4 x - 10
† Buscamos un intervalo donde se cumplan las hipótesis del teorema de convergencia:
Se cumple i) pues f(1) f(2) < 0.
f[1]
−5
f[2]
6
Se cumple ii) pues f'(x)∫0 para todo xœ[1,2]
f'[x]
4 + 3 x2
Y se cumple iii) pues f''(x)>0 en [1,2].
para generar la sucesión tomamos un valor inicial x0 œ[1,2] tal que f(x0 L f '' Hx0 ) > 0. Generalmente se suele tomar
uno de los extremos del intervalo.
f[1] f''[1]
−30
f[2] f''[2]
72
Luego tomamos x0 = 2.
† Aplicamos el método de newton-Raphson con 5 iteraciones
practica6.nb
11
x0 = 2;
f@xn D
F;
f '@xn D
Print@"Solución aproximada = ", N@x5 , 20DD;
x5 − x4
PrintB"Error estimado = ", NBAbsB
F, 2FF
x5
ForBn = 0, n ≤ 4, n ++, xn+1 = xn −
Solución aproximada =
1.5567732643942114633
Error estimado = 5.7 × 10−13
También podemos resolverla utilizando la instrucción FindRoot [ecuación, {x,x0 }]que encuentra un valor
aproximado de la solución de la ecuación dada (en este caso suponemos que en la variable x) partiendo del valor
inicial x0 y aplicando el método de Newton-Raphson.
FindRoot[x^3+ 4 x - 10, {x,2}]
8x → 1.55677<
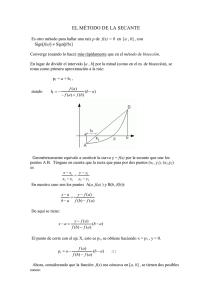
5.-Método de la secante
El método de la secante se puede obtener a partir del método de la cuerda o a partir del método de NewtonRaphson. El procedimiento a seguir a partir del método de la cuerda es similar, pero en este caso se construye
iterativamente una sucesión de valores xk+1 = xk -
xk -xk-1
f Hxk L- f Hxk-1 L
f Hxk L , k = 0,1, .. sin realizar la comprobación de
cambio de signo.
Para obtenerlo a partir del método de Newton-Raphson se sustituye en éste la derivada por el cociente de
diferencias, geométricamente equivale a sustituir la tangente por la secante.
Ahora bien, debemos implementar algún criterio de parada . Lo que haremos ahora es fijarnos en la diferencia entre
dos iteraciones consecutivas, al no poder controlar de forma tan clara como en el método de bisección el error
absoluto cometido, pararemos el proceso cuando la diferencia sea inferior a la tolerancia prefijada.
Ejemplo 5.1 Aplicar el método de la cuerda con 5 iteraciones para resolver la
ecuación 2 x - cos x = 0. Dar una cota del error cometido.
à Definimos la función
f@x_D := 2 x − Cos@xD
à Buscamos un intervalo donde haya alternancia de signo
practica6.nb
12
f@0D
−1
f@1D êê N
1.4597
Presentamos los resultados de todas las iteraciones:
a0 = 0; b0 = 1; niter = 10;
ForBn = 0, n ≤ niter, n ++,
xn = an − f@an D
bn − an
;
f@bn D − f@an D
If@f@xn D 0, Print@"Solución exacta", xn D; Break@DD;
If@f@xn D ≠ 0, an+1 = an ; bn+1 = xn , an+1 = xn ; bn+1 = bn DF;
PrintB"Solución aproximada = ", N@xniter , 20D,
" con error menor que " , NBAbsB
xniter − xniter−1
xniter
F, 20FF
Solución aproximada = 0.45018361129185560400
con error menor que 7.6350037629623176581 × 10−11
FindRoot[2 x - Cos[x]==0,{x,0,1}]
8x → 0.450184<
6. Ejercicios propuestos
Ejercicio 1. Probar que la ecuación x + cos x = 3 tiene solución real única y obtener un valor aproximado de la
solución aplicando el método de la secante con 5 iteraciones y el método de Newton-Raphson con 7 iteraciones.
Estimar el error cometido en cada caso.
Ejercicio 2. ¿Cuántas iteraciones del método de la bisección son necesarias para obtener una solución de la
ecuación x ln x = 4 con 5 cifras decimales exactas?. Hallar la solución.
Ejercicio 3. Aplica el método iterativo de punto fijo para resolver la ecuación e-3 x - x =
0. Dar una estimación del error cometido.