Variables aleatorias.

Estadística
SESIÓN 8: Distribución de probabilidad
discreta. Primera parte.
Contextualización

En la presente sesión seguiremos con el estudio de la
probabilidad introduciendo los conceptos de variable aleatoria,
definiremos variable aleatoria discreta y se darán ejemplos así
como se aprenderá el cálculo del valor esperado y su varianza.
Fuente: http://dc238.4shared.com/doc/hwGWWtYx/preview_html_be91d07.gif
Introducción
 Comúnmente el resultado de
un experimento aleatorio se
denota como un número, al
cual le llamaremos variable
aleatoria.
 En esta ocasión iniciaremos
con el tema: distribución de
probabilidad discreta, en la
siguiente semana
continuaremos con los
subsiguientes subtemas.
Fuente: http://web.educastur.princast.es/conc/lamilagrosa/mate/moneda.JPG
Explicación
Una variable aleatoria proporciona un medio para describir los
resultados experimentales empleando valores numéricos.
Explicación

Variables aleatorias discretas

Es aquella variable aleatoria que asume, ya sea un número finito de
valores o una sucesión infinita de valores tales como 0,1, 2, 3…
Ejemplo:
Experimento
Variable aleatoria(x)
Valores posibles
Llamar a cinco clientes
No.clientes en un pedido
0, 1, 2, 3, 4,5….
Vender un automóvil
Sexo del cliente
0=HOMBRE, 1=MUJER
Explicación

Variable aleatoria continúa.

Es aquella variable que puede tomar cualquier valor numérico
dentro de un intervalo o colección de intervalos.
Ejemplo:
Experimento
Variable aleatoria(x)
Valores posibles
Operar un banco
Tiempo en minutos entre la X ≥ 0
llegada de los clientes
Llenar
una
lata
refresco(máx. 12.1 onzas)
de Cantidad de onzas
0 ≤ x ≤ 12.1
Explicación

Distribuciones de probabilidad discretas

Describen como se distribuyen las probabilidades entre los valores de
la variable aleatoria.

En el caso de una variable aleatoria discreta x, la distribución de
probabilidad está definida por una función de probabilidad, denotada
por f (x).

Ejemplo: construye la función de probabilidad para el número de
artículos defectuosos en una muestra de 2 artículos inspeccionados
al azar.
Explicación
Solución:
El espacio muestral “S” que se tiene es: S = { BB, DB, BD, DD)
X
0
1
2
f(X)
¼
½
¼
x = Número de artículos defectuosos en la muestra.
F(x) = Probabilidad
Con los datos de la tabla de función, responde: ¿Cuál es la probabilidad de tener
un artículo defectuoso? f (1) = ½
Explicación

Condiciones requeridas para una función de probabilidad discreta.

f(x) ≥ 0

∑f(x) = 1

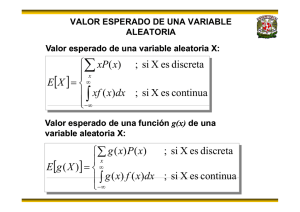
Valor esperado y varianza

El valor esperado o media, de una variable aleatoria es una medida
de localización central. Su fórmula es:

E(x) = µ = ∑xf(x)

Varianza.- Variabilidad en los valores de la variable aleatoria, su
fórmula es:
Var( x)     ( x   ) f ( x)
2
2
Explicación
Ejemplo: Calcular el valor esperado y la varianza para la función de probabilidad
X
0
1
2
f(X)
¼
½
¼
Valor esperado: µ = ∑xf(x) = ∑(0)(1/4)+(1)(1/2)+(2)(1/4)
µ=1
Varianza:
Conclusión

En esta sesión aprendimos sobre variables aleatorias y sus
características, lo que debemos de recordar son los conceptos de valor
esperado y varianza, pues están relacionados con los temas que veremos
más adelante.

En la siguiente sesión estudiaremos la distribución de probabilidad
binomial.
Fuente:
http://recursostic.educacion.es/descartes/web/materiales_didacticos/distribuciones_probabilidad/binomial1.gif
Para aprender más
 En el presente apartado encontrarás más información
acerca del tema para enriquecer tu aprendizaje. Puedes
ampliar tu conocimiento visitando los siguientes sitios de
Internet.
 Variables aleatorias. (s/f). Consultado el 6 de noviembre
de 2013:
http://www.ub.edu/stat/GrupsInnovacio/Statmedia/demo/T
emas/Capitulo2/B0C2m1t0.htm
 Estadística. Ingeniería informática. Curso 2009-2010.
(s/f). Variables aleatorias. Consultado el 6 de noviembre
de 2013:
http://www.uam.es/personal_pdi/ciencias/atorrent/docenc
ia/09-10/temas/1.3.VariablesAleatorias.pdf

Es de gran utilidad visitar el apoyo correspondiente al tema, pues te
permitirá desarrollar los ejercicios con más éxito.
Bibliografía
 Anderson, D., Sweeney, D., Williams, T. (2008).
Estadística para administración y economía. México:
Editorial Cengage Learning.