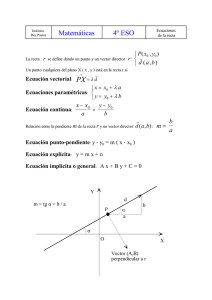
NOTAS SOBRE GEOMETRÍA MÉTRICA

NOTAS SOBRE GEOMETRÍA MÉTRICA
MATEMÁTICA PARA ARQUITECTOS
“El misterio de la Arquitectura se halla en la
geometría. Las formas básicas pasan a ser
fundamentales y la geometría se convierte en el
lenguaje de la Humanidad”
Le Corbusier
-1-
Consideraciones previas:
En la fase inicial del proyecto, durante la esquematización y la propuesta conceptual, se
suele dejar de lado, generalmente, las consideraciones de tipo estructural y se atiende
preferentemente a los aspectos funcionales y formales. Dejar de lado este importante
componente del proyecto es tanto como negar su carácter interdisciplinario, es desconocer
incluso las posibilidades de una acción coordinada entre el campo de la arquitectura y la
ingeniería que, cuando se realiza en el ámbito profesional, suele aportar resultados muy
enriquecedores al propio proyecto.
Conocer las propiedades geométricas de las formas adoptadas es trabajar
constructivamente esas formas.
El triángulo, por ejemplo, es el único polígono que no se deforma
cuando actúa sobre él una fuerza. Al aplicar una fuerza de
compresión sobre uno cualquiera de los vértices de un triángulo
formado por tres vigas, automáticamente las dos vigas que parten
de dicho vértice quedan sometidas a dicha fuerza de compresión,
mientras que la tercera quedará sometida a un esfuerzo de
tracción. Cualquier otra forma geométrica que adopten los elementos de una estructura no
será rígida o estable hasta que no se triangule.
Recurriendo al principio de la triangulación se puede evitar la
deformación de estructuras rectangulares con la llamada “cruz
de San Andrés”
Existen muchas estructuras que están formadas en base a
triángulos unidos entre sí. Este tipo de estructuras, que
adquieren una gran rigidez, tienen infinidad de aplicaciones.
Utilizando el recurso de la triangulación se han
conseguido vigas de gran longitud y resistencia, las
llamadas vigas reticuladas, que se emplean en la
construcción de aquellas edificaciones donde se
necesiten cubrir grandes luces.
Antiprisma
Torre Calabria – Arq Manfredi Nicoletti
La forma que adopta la torre
Calabria, (antiprisma) está pensada
teniendo en cuenta las propiedades del
triángulo, dando lugar a una estructura
indeformable, exigida por la alta
vulnerabilidad sísmica del área.
Es importante conocer entonces los fundamentos de la geometría de estas formas. El
proceso mediante el cual se logra la adquisición de éstos, es arduo, pero no debe verse
como un difícil camino dirigido a lograr el dominio de técnicas de cálculo o determinadas
habilidades gráficas. Debe entenderse como un privilegiado camino hacia la adquisición de
hábitos mentales de creación espacial y destrezas geométricas necesarias para potenciar la
capacidad creativa.
La matemática griega comienza con el mismo nombre con que se inicia la filosofía griega:
Thales de Mileto.
-2-
“Una de las contribuciones geométricas de Thales consistió en determinar la altura de una
pirámide midiendo la sombra proyectada por la misma, en el instante en que su propia
sombra era igual a la altura de su cuerpo” 1
TEOREMA DE THALES
Si se cortan tres o más paralelas con dos transversales, la razón de dos segmentos
cualesquiera de una de las transversales es igual a la razón de los segmentos
r1 // r2 // r3 // r4
a
r1
b
d
c
r2
e
a d
=
b e
a d
=
c f
a+b d +e
=
b
e
a+c d +f
=
b
e
r3
r4
f
Una de las aplicaciones del Teorema de Thales
es la división de un segmento en partes
iguales.
Arco Lobulado
1
A
B
Aplicación de Thales para dividir en seis
partes iguales
Historia de la Matemática. Rey Pastor y Babini
-3-
DIVISIÓN DE UN SEGMENTO EN MEDIA Y EXTREMA RAZÓN
Dado un segmento AB, se dice que está dividido en media y extrema razón: “…si hay de la
parte pequeña a la parte grande, la misma relación que de la parte grande al todo” 1
b
a
=
a a+b
b
a
a
=x
b
a
b
= 1+
b
a
x = 1+
x2 − x −1 = 0
x=
1
x
1± 5
2
a a+b
=
b
a
a a b
= +
b a a
b 1
=
a x
x +1
x=
x2 = x +1
x
a 1+ 5
=
= 1,61803398875...
b
2
Llamado Número de Oro
No se considera el otro valor de x ya que
a
es un número positivo.
b
Los griegos llamaron Rectángulo de Oro, a un rectángulo cuyos lados están en proporción
áurea, es decir su razón (cociente) es el número de oro.
División de un rectángulo áureo en rectángulos proporcionales:
A partir del rectángulo áureo, subdividido en
rectángulos proporcionales obtenemos la
única espiral que puede construirse con
regla y compás: la Espiral Áurea
1
Vitruvio
-4-
Salvador Dalí: Apéndice.
Una espiral áurea controla toda la composición del cuadro
En templos de la antigua Grecia y Roma aparecen
rectángulos dinámicos, especialmente áureos, en la
conformación de espacios.
-5-
El rectángulo dinámicos, según Jay Hambidge1, es aquel en el que la relación de su lado
mayor al menor es un número irracional. En cambio, aquellos rectángulos que dan razones
enteras o racionales son, en general, estáticos. Algunas relaciones enteras o racionales
resultan ser estáticas y dinámicas al mismo tiempo como, por ejemplo, un rectángulo de
razón 2 = 4 .
TEOREMA DE PITÁGORAS
En todo triángulo rectángulo, el cuadrado de la hipotenusa
es igual a la suma de los cuadrados de los catetos.
a
b
a2 = b2 + c 2
Cuando se trabaja con triángulos, los elementos principales
para su caracterización son: lados y ángulos.
c
La parte de la matemática que se dedica a encontrar las relaciones entre los lados y los
ángulos de un triángulo es la Trigonometría.
En principio encontremos relaciones trigonométricas en el triángulo rectángulo.
En la figura tenemos varios triángulos semejantes (por tener sus tres ángulos iguales,
condición de ángulos entre paralelas)
La razón entre los catetos de estos triángulos rectángulos es constante
(propiedad de Thales)
Esta razón depende de la inclinación de la hipotenusa (ángulo que forma
con el cateto) y recibe el nombre de tangente del ángulo:
tg α =
a
b
cateto opuesto
cateto adyacente
Las otras razones trigonométricas relacionan los catetos con la hipotenusa:
a
sen α =
h
cos α =
b
h
Cateto opuesto
Hipotenusa
Cateto adyacente
Hipotenusa
Estas definiciones se cumplen sólo en triángulos rectángulos.
Para la resolución de triángulos oblicuángulos (no rectángulos) contamos con:
Teorema del seno
1
sen α sen β sen δ
=
=
a
b
d
Jay Hambidge (13 de enero de 1867– 20 de enero de 1924) fue un artista estadounidense nacido en Canadá.
-6-
Teorema del coseno:
a2 = b2 + d2 − 2bd.cos α
b2 = a2 + d2 − 2ad.cos β
d2 = a2 + b2 − 2ab.cos δ
C
PUNTOS NOTABLES DEL TRIÁNGULO
Si trazamos las mediatrices de los lados de un triángulo
cualquiera, observamos que se cortan en un único punto O,
llamado circuncentro, que está a igual distancia de los tres
vértices del triángulo
O
A
El punto de intersección de las tres mediatrices es el centro de
una circunferencia que pasa por los tres vértices del triángulo,
que llamaremos circunferencia circunscripta. Fig1
B
Fig1
Las bisectrices de los tres ángulos de un triángulo se cortan en
un punto I que está a igual distancia de los tres lados y que recibe
el nombre de incentro.
C
Fig 2
El punto de intersección de las tres bisectrices es el centro de un
circunferencia tangente a los tres lados del triángulo, que
llamaremos circunferencia inscripta. Fig2
I
A
Las tres medianas de un triángulo, se cortan en un único punto,
llamado baricentro.
B
En cualquier triángulo, el baricentro siempre es interior al
mismo, más aún, es el centro de gravedad del triángulo y se
denotará por G. El baricentro de un triángulo, es un punto
interior al mismo. La distancia del baricentro a un vértice es el
doble de la distancia del baricentro al punto medio del lado
opuesto. Fig 3
C
Fig 3
G
A
Se llaman alturas de un triángulo a cada uno de los tres segmentos que son perpendiculares
a un lado y pasan por el vértice opuesto.
Las tres alturas se cortan en un punto llamado ortocentro. Fig4
-7-
B
C
H
C
Fig4
B
H
A
A
B
Polígonos
Se llama polígono a la figura geométrica plana limitada por
segmentos rectos consecutivos no alineados.
Polígonos Convexos
Definición: Dados en el plano tres o más puntos en un cierto
orden, por ejemplo ARMJ, tales que tres consecutivos no estén
alineados y que la recta determinada por dos consecutivos
cualesquiera deje a los demás en un mismo semiplano con
respecto a ella, se llama polígono convexo ARMJ
a la
intersección de esos semiplanos.
Polígonos Cóncavos
Definición: Se dice que un polígono es cóncavo, cuando dados los
semiplanos determinados por las rectas que contienen los lados del
mismo, al menos en un caso la figura queda en distintos
semiplanos
Polígonos Regulares
Definición: Se dice que un polígono es regular, cuando tiene todos sus lados y sus ángulos
respectivamente iguales.
-8-
n = número de lados l = longitud del lado
Perímetro = l . n
Área triángulo =
b.h
2
Área cuadrado = L2 =
D2
2
Área polígonos (más de cuatro lados)=
Perímetro. Apotema
2
Determinación de tipos de polígonos estrellados
Siendo
p = cantidad de vértices
d = paso entre vértices
Se tiene el polígono n = p/d tal que d < ½ p
Si el resto del cociente (p/d) es 0 (cero), el polígono es Pseudoestrellado
Si el resto del cociente (p/d) es diferente a 0 (cero), el polígono es Estrellado
EJEMPLO:
p = 16
p/d = 16/1 Polígono de 16 lados
p/d = 16/2 Pseudoestrellado
p/d = 16/3 Estrellado
p/d = 16/4 Pseudoestrellado
p/d = 16/5 Estrellado
-9-
p/d= 16/6 = 8/3 Estrellado
p/d = 16/7 Estrellado
Polígonos estrellados y pseudoestrellados en mosaicos.
Ángulo Diedro
Dos planos que se cortan determinan cuatro regiones en el
espacio, cada una de las cuales se llama ángulo diedro.
Ángulo Triedro
Dadas tres semirrectas no coplanares, de origen común,
se llama ángulo triedro a la figura formada por los puntos
comunes a los diedros cuyas aristas son esas mismas
semirrectas.
En el ángulo triedro trirrectángulo los planos que se
intersecan resultan perpendiculares dos a dos.
Ángulo poliedro
Tres o más semirrectas no coplanares que tienen un mismo origen determinan un ángulo
poliedro.
- 10 -
Cuerpos poliedros
Un cuerpo es un poliedro cuando tiene todas sus
caras planas.
Prisma: Es el poliedro cuyas caras laterales son
paralelogramos y cuyas bases son polígonos
paralelos e iguales entre sí.
Área lateral= Perímetro de la base . Altura
Área total= Área lateral + 2 . Área de la base
Volumen
= Área de la base . Altura
Pirámide: Es el poliedro en el cual todas las caras,
menos una, tienen un vértice en común.
Área lateral = ½ . Perímetro . Apotema lateral
Área total = Área lateral + Área de la base
Volumen = 1/3 . Área de la base . Altura
Poliedros regulares o Sólidos de Platón
Definición: Se dice que un poliedro convexo es regular si sus caras son polígonos regulares
congruentes y a cada vértice concurre el mismo número de caras.
Con caras triangulares:
60 °
60 °
60 °
TETRAEDRO
- 11 -
60 °
60 °
60 °60 °
OCTAEDRO
60 °
60 °
60 °
60 °60 °
ICOSAEDRO
Con caras cuadradas
90 °
90 °
90 °
HEXAEDRO o CUBO
Con caras pentagonales
108 °
108 °
108 °
DODECAEDRO
Sólidos de Platón
Las particulares propiedades de estos poliedros son conocidas desde la antigüedad clásica,
figurando ya una descripción detallada de los mismos en Los elementos de Euclides. Se les
llegaron a atribuir incluso propiedades mágicas o mitológicas; en el Diálogo de Platón
(Timeo) dice «El fuego está formado por tetraedros; el aire, de octaedros; el agua, de
- 12 -
icosaedros; la tierra de cubos; y como aún es posible una quinta forma, Dios ha utilizado
ésta, el dodecaedro pentagonal, para que sirva de límite al mundo».
La Última Cena. Salvador Dali - 1955
Propiedades
Regularidad
•
•
•
•
Todas las caras de un sólido platónico son polígonos regulares iguales.
En todos los vértices de un sólido platónico concurren el mismo número de caras y
de aristas.
Todas las aristas de un sólido platónico tienen la misma longitud.
Todos los ángulos diedros que forman las caras de un sólido platónico entre sí son
iguales.
Simetría
•
•
•
Todos ellos gozan de perfecta simetría central respecto a un punto del espacio
(centro de simetría) que equidista de sus caras, de sus vértices y de sus aristas.
Todos ellos tienen además simetría axial respecto a una serie de ejes de simetría
que pasan por el centro de simetría anterior.
Todos ellos tienen también simetría especular respecto a una serie de planos de
simetría (o planos principales), que los dividen en dos partes iguales.
Como consecuencia geométrica de lo anterior, se pueden trazar en todo sólido platónico tres
esferas particulares, todas ellas centradas en el centro de simetría del poliedro:
• Una esfera inscrita, tangente a todas sus caras en su centro.
• Una segunda esfera tangente a todas las aristas en su centro.
• Una esfera circunscrita, que pase por todos los vértices del poliedro.
Proyectando las aristas de un poliedro platónico sobre su esfera circunscrita desde el centro
de simetría del poliedro se obtiene una red esférica regular, compuesta por arcos iguales de
círculo máximo, que constituyen polígonos esféricos regulares.
Dualidad
Si se traza un poliedro empleando como vértices los centros de las caras de un sólido
platónico se obtiene otro sólido platónico, llamado dual del primero, con tantos vértices como
caras tenía el sólido inicial, y el mismo número de aristas. El poliedro dual de un dodecaedro
es un icosaedro, y viceversa; el de un cubo es un octaedro; y el poliedro dual de un
tetraedro es otro tetraedro.
- 13 -
Formas poliédricas conformando espacios
Arq. Piet Blom. Casas cubo. Rotterdam
Arq. Peter Eisenman. House III
Koji Tsutsui Architect & Associates
Casa minimalista
Cuerpos de rotación
Son los que se generan mediante la rotación o el giro de una figura plana alrededor de un
eje.
Cilindro
Área lateral = 2.π .r.h
Área total = área lateral + 2.π .r 2
Volumen = π .r 2 .h
Cono
Área lateral = π .r.g
Área total = área lateral + π .r 2
Volumen =
π .r 2 .h
- 14 -
3
Esfera
Área total = 4.π .r 2
Volumen =
4
.π .r 3
3
Las formas puras caracterizan la obra del Arq. Tadao Ando
Convention and Exhibition Center.
Arq. Rem Koolhas. Dubai
Casa unifamiliar. Stabio, Suiza.
Arq. Mario Botta. 1981
- 15 -
Cantina Petra. Suvereto, Italia
Arq. Mario Botta. 2003
Oficinas Harting-Minden, Alemania
Arq. Mario Botta 2001
- 16 -
NOTAS SOBRE TRANSFORMACIONES EN EL PLANO
MATEMÁTICA PARA ARQUITECTOS
“A menudo me encuentro más cerca de los
matemáticos que de mis colegas los artistas”
M. C. Escher
- 17 -
TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO
Llamamos transformación geométrica a una operación u operaciones que permiten deducir una
nueva figura, de la primitivamente dada. El transformado se llama Homólogo del original.
CLASIFICACIÓN DE LAS TRANSFORMACIONES GEOMÉTRICAS
Tenemos una primera clasificación de las transformaciones:
•
•
Directa: cuando conservan el sentido en el plano orientado.
Inversa: cuando el sentido del original y el homólogo son contrarios.
Tenemos otra clasificación en función del aspecto de la figura transformada con respecto a la
original:
•
•
•
Isométricas o Movimientos: es una transformación geométrica del plano que conserva
los ángulos y las distancias (la forma y el tamaño). Es una transformación que le hace
corresponder a una figura dada, otra igual o congruente con ella, en otra posición.Se
distinguen tres tipos de movimientos: Traslación, Rotación y Simetría.
Isomórficas: es una transformación geométrica en el plano, en la cual, la figura
transformada, conserva la forma (los ángulos) pero han cambiado la posición y el tamaño.
Existe proporcionalidad entre las dimensiones de la figura original y la transformada. En
esta transformación encontramos la Homotecia.
Anamórficas: es una transformación a partir de la cual, cambia la forma de la figura
original. En esta transformación encontramos la Inversión
1.- TRASLACIÓN
Definición: Se llama traslación T de vector libre V a
una transformación que asocia a cada punto A del
plano otro punto del mismo plano A’=T(A) de manera
que el vector AA’ sea igual al vector V.
Todo vector libre
características:
• su módulo
• su dirección
• su sentido
queda
determinado
por
tres
Los vectores equipolentes, también llamados iguales, son
aquellos que tienen la misma dirección (están incluidos en
rectas paralelas), sentido y módulo.
Un punto o una figura, es invariante por un movimiento (también se dice que es doble),
cuando se transforma en sí mismo al aplicarle dicho movimiento.
- 18 -
Vector
B
C
D
TV ABCDE = A' B' C' D' E'
B'
A
E
D'
A'
C'
E'
Construcción: para obtener el polígono A’B’C’D’E’ basta con aplicar vectores equipolentes al
vector V por cada uno de los vértices del polígono ABCDE, se obtienen así los vértices
homólogos.
Toda figura transformada por una traslación conserva la medida de sus lados y ángulos.
C''
C
B''
B
COMPOSICIÓN DE TRASLACIONES
D''
D
La composición de dos traslaciones de vectores V y U,
es otra traslación de vector V+U.
C'
A
E
A''
E''
B'
D'
TU .TV = T(U + V)
A'
E'
V+U
La traslación T(U + V) se llama compuesta de TV y TU
T(U) .T(V) ABCDE = A' ' B' ' C' ' D' ' E' '
V
U
RECONOCIMIENTO DE LAS TRANSFORMACIONES Y SU NOTACIÓN: TRASLACIÓN
Calculamos las componentes del vector con el que se
realiza la traslación
A'
(4,00; 6,00)
B'
V = ( 4 − 1 ; 8 − 2)
V = (3 ; 6)
C'
A (1,00; 2,00)
B
1
NOTACIÓN:
1
C
- 19 -
T
ABC = A ' B ' C '
3, 6
(
)
2.- ROTACIÓN
Definición: Se llama rotación de centro O y ángulo ß a un
movimiento que hace corresponder a cada punto P del plano, otro
punto P' del mismo plano, tal que: d(O, P) =d (O, P') y ángulo
(POP') = ß.
P
P'
b
O
Además, el ángulo POP' y el ß deben tener el mismo sentido de
giro.
Por convención se llama sentido positivo de un ángulo, al sentido contrario al de las agujas
del reloj.
R (O, −68º ) ABCDE = A' B' C' D' E'
Para determinar una rotación, además de la figura a rotar,
necesitamos:
B'
C
B
D
A'
E'
A
•
•
•
D'
C'
un centro de rotación.
un ángulo de rotación.
un sentido de giro (positivo o negativo).
E
O
El centro de rotación no siempre es exterior a la figura a
rotar.
COMPOSICIÓN DE ROTACIONES
La composición de rotaciones del mismo centro, es igual a
otra rotación con el mismo centro, cuyo ángulo de rotación es
igual a la suma algebraica de los ángulos dados
R (O, 38º) . R (O, 105º) ABCDE
- 20 -
RECONOCIMIENTO DE LAS TRANSFORMACIONES Y SU NOTACIÓN: ROTACIÓN
B'
A'
Para encontrar el centro de la rotación se trazan dos
segmentos que unan vértices homólogos. A cada uno de ellos
se le traza la mediatriz. El punto de intersección de ambas
mediatrices es el centro de rotación. Fig1
C'
O
A
Fig.1
B
C
B'
A'
O
Para calcular la amplitud del ángulo de rotación, se mide el
ángulo que forman dos vértices homólogos con el centro de
rotación Fig.2
C'
NOTACIÓN:
83,0 °
A
C
B
R
(O; 83 ) ABC = A ' B ' C '
Fig.2
3.- SIMETRÍA
Simetría axial
Definición: Se llama simetría axial S, de eje e, a un movimiento que transforma un punto P del
plano, en otro P' del mismo plano, de modo que e es mediatriz del segmento PP'.
e
Construcción con regla y compás. Para construir el
simétrico del punto P respecto de la recta e, basta con trazar
una perpendicular a e por P. Desde el punto O de
intersección, trazar una circunferencia de radio OP, el corte
con la perpendicular determina el punto P’, simétrico de P
respecto de e. A la recta e se la denomina eje de simetría.
El punto P’ es el transformado de P, es decir su imagen.
- 21 -
90,0 ° P'
O
P
De esta forma podríamos hacer la simetría axial de segmentos, polígonos, etc. bastaría con
hacer el simétrico de cada punto y unir los puntos obtenidos.
Eje de simetría
r
B'
A'
S r ABCDE = A' B' C' D' E'
D'
E'
B
C'
D
A
C
Hay muchas figuras invariantes mediante simetrías axiales.
Se las llama figuras simétricas. Los polígonos regulares lo
son.
E
COMPOSICIÓN DE SIMETRÍAS AXIALES
Ejes paralelos:
La composición se convierte en una traslación,
cuyo desplazamiento es el doble de la distancia
entre ejes.
Ejes que se cortan:
La composición se convierte en una rotación de
centro en el corte de los ejes y ángulo el doble del
que forman los ejes.
RECONOCIMIENTO DE LAS TRANSFORMACIONES Y SU NOTACIÓN: SIMETRÍA AXIAL
- 22 -
M
B
A
B'
A'
C
Para reconocer el eje de simetría se
traza un segmento que una dos vértices
homólogos AA ' , BB ' o CC '
y se
construye la mediatriz del mismo
C'
NOTACIÓN: SMN ABC = A ' B ' C '
N
Simetría central
Definición: La simetría central de centro o de un punto P es
otro punto P' verificando que:
• El punto O (centro) equidista de los puntos P y P'.
• Los puntos O, P y P' están alineados.
P
O
P'
La simetría central de centro O es equivalente a una rotación de centro O y de amplitud 180º.
Construcción con regla y compás:
Para construir el simétrico P’ de un punto P respecto
a otro O, basta con trazar la recta que une P con O.
Con centro en O se traza una circunferencia de radio
OP. La intersección de la recta y la circunferencia
determina P’.
B
C
D
A
E'
O
E
A'
D'
C'
B'
SO ABCDE = A' B' C' D' E'
COMPOSICIÓN DE SIMETRÍAS CENTRALES
La composición de dos simetrías centrales de centros O1 y O2 es una traslación según un vector
cuyo módulo es el duplo de la distancia entre los centros y de igual dirección y sentido que las
del vector O1O2.
- 23 -
B
D
S (O2 ) .S (O1 ) ABCDE = A' ' B' ' C' ' D' ' E' '
A
B''
O1
E'
A'
D'
C''
D''
A''
E
C
O2
C'
B'
E''
RECONOCIMIENTO DE LAS TRANSFORMACIONES Y SU NOTACIÓN: SIMETRÍA CENTRAL
A
Para encontrar el punto a partir del cual se
realizó la simetría central, se trazan rectas que
unan vértices homólogos. El punto de
intersección de estas rectas indica el centro de
simetría.
B
C
O
C'
B'
A'
NOTACIÓN:
So ABC = A ' B ' C '
HOMOTECIA
Se llama homotecia de centro O y razón k, a la transformación que a todo punto P, del plano, le
hace corresponder otro P’, tal que OP’ = k . OP (k ≠ 0)
Se dice que P’ es el homotético de P, por la homotecia dada.
P'
k=2
P
OP' = 2.OP Los vectores OP y OP' tienen el mismo sentido.
O
k=
1
2
P
P'
O
1
OP' = .OP Los vectores OP y OP' tienen el mismo sentido.
2
- 24 -
P
k=-2
OP' = −2.OP P y P’ pertenecen a semirrectas opuestas.
O
P'
H (O,2) ABCDE = A' B' C' D' E'
B'
D'
A'
B
D
A
E
E'
C'
C
O
•
El centro de homotecia es el punto en el que concurren las rectas que determinan los puntos
de una figura y sus correspondientes homólogos: O
•
La razón de homotecia se calcula hallando el cociente entre OA ' y OA , siendo A un punto
cualquiera. El signo de ésta dependerá de la posición de O respecto de A y A'.
•
Una homotecia transforma un segmento AB en otro paralelo A 'B' , k veces el primero. En
consecuencia, la razón también se halla dividiendo la longitud de dos segmentos homólogos.
RECONOCIMIENTO DE LAS TRANSFORMACIONES Y SU NOTACIÓN: HOMOTECIA
A'
B'
A
C'
B
Para encontrar el centro de la homotecia se unen
vértices homólogos, siendo este centro, la intersección de
estas proyecciones.
Para calcular el factor de homotecia se realiza el cociente
entre: OA ' , en este caso OA ' = 2
OA
OA
C
O
NOTACIÓN:
- 25 -
H(O, 2) ABC = A ' B ' C '
COMPOSICIÓN DE MOVIMIENTOS
Para componer dos movimientos se debe aplicar el primero de ellos al objeto inicial; se obtendrá
un transformado; a este transformado se le aplica el segundo movimiento y se obtiene el objeto
final, resultado de la composición.
V
B''
e
D''
B' C''
D'
B
D
A
C
C'
A''
E''
A'
E'
E
CONGRUENCIA
Dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u
orientación sean distintas. Las partes coincidentes de las figuras congruentes se llaman
homólogas o correspondientes.
SEMEJANZA
Se llama semejanza a toda composición de un movimiento con una homotecia.
En toda semejanza los ángulos son iguales y los segmentos proporcionales.
O
A
La razón de los segmentos homotéticos
es igual a la razón de homotecia:
A'
A' B ' A' C ' B ' C '
=
=
=k
AB
AC
BC
C
B
Como la amplitud de los ángulos se
conserva en la homotecia:
Aˆ = Aˆ ' Bˆ = Bˆ ' Cˆ = Cˆ '
B'
C'
En consecuencia los triángulos transformados son semejantes.
SIMETRIA DE ROTACIÓN O ROTACIONAL
Algunas veces llamada simetría de giro. Una figura tiene simetría rotacional alrededor de un
punto O si se puede hacer que coincida exactamente sobre el original cuando se rota alrededor
- 26 -
de O un cierto ángulo menor a un ciclo completo. El orden de rotación será igual al número de
veces que coincida.
Simetría rotacional de
orden 4
Simetría rotacional de
orden 2
COMPOSICIÓN DE TRANSFORMACIONES
ABCDEF = A ' B ' C ' D ' E ' F '
SBE T2
CD
D
C
B
A
A'
C' B'
D'
F
E
F'
La operación que se indica es: aplicar al polígono
ABCDEF, la simetría axial, de eje BE, de la traslación
de vector 2CD. Esto implica que deberemos realizar
primero la traslación, para luego simetrizar ese polígono
trasladado. El polígono obtenido es el A’B’C’D’E’F’.
E'
TRANSFORMACIONES GEOMÉTRICAS EN ARQUITECTURA
Arq. Charles Gwathmey (EEUU-1938)
Residencias Bridgehampton 1970
R (O, −132,5) .TV
α = -135,2
V
- 27 -
O
M
R (M, -134,3º) .H (O;2,3)
Sayamaike Historical Museum – Osaka Japón
Arq. Tadao Ando
H
2
(O, )
5
.R (M, −90º )
En la obra del Arq. Santiago Calatrava la simetría que se produce con el espejo de agua permite
una lectura muy particular al pabellón Hemisferic del parque oceanográfico de La Ciudad de
Artes y Ciencias en Valencia.
La homotecia aplicada a los planos curvos delimita espacios de gran riqueza arquitectónica en la
obra de Richard Meier.
- 28 -
L’Hemisferic. España
Arq. S. Calatrava
Iglesia del Jubileo. Roma
Arq. R. Meier
TESELADOS
Diseños de figuras geométricas que por sí mismas cubren una superficie plana, sin dejar huecos
ni superponerse.
•
Regulares
•
Semirregulares
La palabra tesela proviene del latín “tessellae”, nombre dado por los romanos a las pequeñas
baldosas usadas en pavimentos y paredes en la antigua Roma.
Los teselados pueden clasificarse según su periodicidad: si el teselado se puede desplazar en
dos direcciones independientes del plano y hacer que coincida consigo mismo, se dirá que es
periódico. Si no, se hablará de teselado no-periódico o aperiódico.
Sorprendentemente sólo hay 17 teselaciones periódicas posibles, y tal vez más sorprendente es
el hecho de que en el palacio de la Alhambra de Granada, España, se pueden encontrar estas
17 teselaciones en los mosaicos que adornan los pisos, paredes, columnas y techos.
Al tener prohibida la representación de seres vivos, el arte musulmán se especializó en este tipo
de creaciones geométricas. En ellas se utiliza la tesela básica (como unidad), la cual se extiende
a todo el plano, mediante los elementos del grupo de simetría correspondiente. Por ejemplo en
- 29 -
el baño del Palacio Comares encontramos
una tesela básica obtenida de un triángulo
equilátero.
Detalle de “La pajarita” en el baño del Palacio Comares.
Detalle “Patio de los Leones”.
Detalle de la ornamentación en las paredes de la Alhambra de Granada
Transformaciones en el Arte
Mauricius Escher siempre indagó acerca de grafismos que tenían un origen matemático:
simetrías, rotaciones, traslaciones a partir de un polígono regular. La obsesión con este tipo de
dibujos, nace a partir de su visita a la Alhambra.
- 30 -
NOTAS SOBRE GEOMETRÍA ANALÍTICA DEL PLANO Y
DEL ESPACIO
MATEMÁTICA PARA ARQUITECTOS
“Mira dos veces para ver lo exacto.
Mira una sóla vez para ver lo bello.”
Henry F. Amiel
- 31 -
Vectores fijos
Un vector es un segmento de una determinada longitud (denominada módulo), al cual se le
asignan las propiedades de dirección y sentido. El punto de origen en el espacio se
denomina punto de aplicación.
Vectores en R2 – Enfoque geométrico
Representación Gráfica: La representación gráfica de un vector se realiza empleando una
flecha o segmento orientado.
B
Q
D
AB
P
CD
PQ
A
C
Origen del vector: A , P y C
Extremo del vector: B , Q y D
Notación:
R
µ
RS = µ
S
Elementos de un vector:
B
a) Dirección
ν
b) Sentido
A
c) Módulo ν ≥ 0 / ν = AB = medida AB
Vectores Opuestos
y ν son vectores opuestos porque tienen la misma dirección, el mismo módulo pero
diferente sentido.
µ
µ = −ν
ν
ν = −µ
µ
- 32 -
Igualdad o equipolencia de vectores
Dos vectores se dicen iguales o equipolentes cuando tienen igual dirección, sentido y
módulo.
µ
µ
b
ν
ν
a
µ =ν
a =b
w
µ =ν = w
Operaciones con vectores
Adición
La suma de dos vectores µ y ν es otro vector que llamamos vector suma o vector
resultante que se puede obtener gráficamente aplicando:
a) Regla del paralelogramo
b) Regla del polígono
Nota: Si µ y ν tienen la misma dirección, entonces:
µ
µ
ν
ν
ν
µ
µ
µ +ν
µ +ν
- 33 -
ν
La adición cumple con las condiciones de ser conmutativa y asociativa
µ +ν = ν + µ
µ + (ν + w) = (µ + ν ) + w
Sustracción
La resta de dos vectores µ y ν
es otro vector que llamamos vector resta
µ −ν = µ + (−ν )
Gráficamente lo podemos obtener aplicando:
a) Regla del paralelogramo
b) Regla del polígono
Producto de un escalar por un vector
Sea k ∈ R , el producto escalar k por un vector µ se simboliza k. µ
El resultado es un vector
k µ = v cuyos elementos son:
•
Módulo de v :
•
•
Dirección de ν : igual a la dirección de µ
Sentido de ν :
Si k > 0 el sentido de ν es igual al de µ
Si k < 0 el sentido de ν es opuesto al de µ
ν = kµ = k . µ
- 34 -
µ
−µ
− 3µ
2µ
k∈R ,k ≠ 0
µ y - µ son vectores opuestos
k. a = b resulta b || a
b || a entonces uno cualquiera de ellos resulta de multiplicar al otro por una constante
Si
no nula
k.a = b ↔ a || b
Vectores en R2 – Enfoque algebraico
Considerando un sistema cartesiano ortogonal. Sea P un punto del plano de coordenadas
(ax,ay)
y
ay
P
P(a , a )
x y
a
OP = a = (a x , a y )
o
ax
x
ax y ay : componentes del vector a
ax : Primera componente
ay : Segunda componente
El vector del plano queda expresado como un par ordenado de números reales. Las
componentes de un vector con origen en el origen de coordenadas son las coordenadas del
extremo del vector.
Igualdad de vectores:
a = (a x , a y )
b = (b x , b y )
a=b ⇔
Módulo:
a = (a x , a y )
a = a x2 + a y2
- 35 -
a x = bx , a y = bx
Operaciones con vectores
Adición
a + b = (a x ,a y ) + (b x ,b y ) = (a x + b x , a y + b y )
Sustracción
a-b = a + (-b) = (a x ,a y ) + (-b x ,-b y ) = (a x − b x , a y − b y )
Producto de un escalar por un vector
k.a = k (a x , a y ) = (k.a x , k.a y )
Producto escalar o producto punto
Esta operación distinta a las vistas anteriormente, determina como resultado en este caso,
un escalar, es decir, un número. El producto escalar de dos vectores a y b se simboliza
a .b
a) Definición 1: Definición cartesiana del producto escalar
a = (a x , a y )
b = (b x , b y )
a .b = a x .b x + a y .b y
b) Definición 2: Interpretación geométrica del producto escalar
a .b = a . b . cos α
( a ≠ 0 y b ≠ 0)
a
y b por lo que 0º ≤ α ≤
Donde α es el menor ángulo no negativo entre los vectores
180º
a
α
b
De la definición surge
a .b > 0 ⇒ 0 ≤ α < 90 º
a .b < 0 ⇒ 90 º < α ≤ 180 º
a .b = 0 ⇒ α = 90 º ⇒ a ⊥ b
Criterio de Perpendicularidad
Los vectores a y b son perpendiculares (ortogonales) sí y sólo sí su producto escalar o
producto punto es igual a cero.
a .b = 0
a ⊥ b ⇔ a .b = 0
- 36 -
Condición de Paralelismo
Si a || b , a y b tienen la misma dirección y por lo tanto cualquiera de ellos resulta de
multiplicar al otro por una constante no nula
b = k. a
k∈R , k ≠ 0
(b x , b y ) = k (a x , a y )
(b x , b y ) = (k a x , k a y )
by = k ay
bx = k ax
bx by
=
ax ay
Resulta
k=
despejando k
∴
bx
ax
y
k=
by
ay
b
b
a || b ⇔ x = y
ax ay
Ángulo determinado por dos vectores
Y
b = (b x , b y )
a = (a x , a y )
a
α
Sabemos que: a .b = a . b . cos α
b
a .b = ax .bx + ay .by
X
Resulta que: a . b . cos α = a x .b x + a y .b y
cos α =
a x .b x + a y .b y
a.b
∴
α = arccos (
a x .b x + a y . b y
)
a.b
Componentes de un vector
Las componentes de un vector AB se pueden obtener restando a las coordenadas del
extremo las coordenadas del origen.
B
yB
B-A
A
yA 0
XA
XB
- 37 -
→
AB = (XB − X A , YB − YA )
Hay infinitos vectores libres iguales o equipolentes. Para obtenerlos basta con trasladar uno
cualesquiera de ellos. Uno Cualquiera de ellos representa a todos los demás, desde un
punto de vista geométrico podemos decir que todos los vectores equipolentes determinan la
misma traslación. De todos los vectores iguales o equipolentes se elige como representante
el que tiene su origen en el origen de coordenadas.
Distancia entre dos puntos del plano
y
yB
B
d(A,B) = AB
d(A,B) = (XB − XA , YB − YA )
A
yA
0
xA
xB
d(A,B) = (XB − X A )2 + (YB − YA )2
x
Expresión cartesiana de un vector del plano
P(u , u )
1 2
µ = OP = (u , u )
1 2
µ = (u , u ) = (u ,0 ) + (0, u )
1 2
1
2
(u , u ) = µ (1,0) + µ (0,1)
1 2
1
2
(u , u ) = µ i + µ j
1 2
1
2
Donde i y j son vectores de módulo 1 llamados versores fundamentales y apuntan en el
sentido positivo de las x e y respectivamente.
Ecuación de la recta en el plano
1) Con vector director y punto
a) Ecuación vectorial
Para obtener la ecuación vectorial de la recta, no es suficiente considerar la dirección de la
recta mediante un vector, porque con esa misma dirección existen infinitas rectas. Es
necesario además, saber por dónde debe pasar ésta, es decir un punto determinado dentro
del plano.
Así tendremos:
P0 (X 0 , Y0 ) ∈ r
o sea: un punto P0 que pertenece a la recta r
a = (a x , a y )
a || r donde a se denomina vector director de la recta o vector asociado.
- 38 -
Para obtener la ecuación vectorial de la recta, se debe considerar otro punto genérico P de
la
→
misma.
→
Aplicando
→
OP = OP0 + t a
la
regla
del
polígono:
→
→
→
OP = OP0 + P0P
reemplazando
donde t ∈ R
∴
(x, y) = (x 0 , y 0 ) + t(a x , a y )
b) Ecuaciones paramétricas de la recta
Partiendo de la ecuación vectorial y operando en el segundo miembro obtendremos:
(x, y) = (x 0 , y 0 ) + t(a x , a y )
x = x 0 + ta x
(x, y) = (x 0 + ta x , y 0 + ta y )
Donde el número real t se denomina parámetro
y = y0 + ta y
c) Ecuación simétrica de la recta
Despejando t en las ecuaciones anteriores
x = x 0 + ta x
Si ax ≠ 0 y ay ≠ 0
resulta
y = y 0 + ta y
∴
t=
t =
x − x0
ax
y − y0
ay
x − x 0 y − y0
=
ax
ay
Nota: ax y ay no pueden ser ambos nulos, pero sí uno de ellos. Sea por ejemplo
P0
r
P0
a
a
r
ay = 0
a = (a x , 0)
ax = 0
r || Eje x
a = (0, a y )
r || Eje y
r ⇒ y = y0
r ⇒ x = x0
d) Ecuación general o implícita de la recta
Partiendo de la ecuación simétrica de la recta.
- 39 -
x − x0 y − y0
=
ax
ay
Si ax ≠ 0 y ay ≠ 0
operando
Ax + By + C = 0
e) Ecuación explícita de la recta
Partiendo de la ecuación implícita.
y=-
Si B ≠ 0
A
C
xB
B
y = mx + b
Donde m= pendiente
m=
var iación de ordenadas
var iación de abscisas
b = ordenada al origen
2) Con dos puntos
Es posible determinar la ecuación de una recta del plano, conociendo dos puntos que
pertenecen a la recta, ya que por esos dos puntos solamente puede pasar una sola recta.
P1(X 1, Y1)
P2 (X 2 , Y2 )
P1 ∈ r
P2 ∈ r
a) Ecuación vectorial de la recta
(x, y) = (x1, y1 ) + t P1P2
P1 (x1 , y1)
(x, y) = (x 2 , y 2 ) + t P1P2
(x, y) = (x 1, y1 ) + t (x 2 - x 1, y 2 - y1 )
P2 (x2 , y2)
(x, y) = (x 2 , y 2 ) + t (x 2 - x1, y 2 - y1 )
r
b) Ecuaciones paramétricas de la recta
Partiendo de la ecuación vectorial y operando en el segundo miembro obtendremos:
x = x1 + t (x 2 - x1)
y = y1 + t (y 2 - y1)
Donde el número real t se denomina parámetro
- 40 -
c) Ecuación simétrica de la recta
Despejando t en las ecuaciones anteriores
x − x 1 y − y1
=
x 2 - x 1 y 2 - y1
Con x1 ≠ x2 y y1 ≠ y2
d) Ecuación segmentaria de la recta
Caso particular
Los puntos datos son las intersecciones de la recta con los ejes coordenados
P1(a,0)
y
P2
P2 (0,b)
reemplazando en la ecuación simétrica resulta
b
x−a y−0
=
0-a b-0
P1
0
−
x
y
+ 1=
a
b
x
a
x y
+ =1
a b
∴
a: abscisa al origen
b: ordenada al origen
Paralelismo
Si las rectas r1 y r2 son paralelas, los vectores directores resultarán paralelos. Las
componentes homólogas de los vectores directores de estas rectas, deben ser
proporcionales.
ax ay
=
bx by
Si
por propiedades de las proporciones,
a = (a x , a y )
b = (bx , b y )
∴
by a y
=
bx ax
mr1 = mr2
Dos rectas no perpendiculares al eje de ordenadas son paralelas sí y sólo sí sus pendientes
son iguales.
Perpendicularidad
r1
a = (a x , a y ) r2
r1 ⊥ r2
a⊥b
⇒
a.b = 0
ax .bx + ay.by = 0
Puede escribirse entonces que: ax .bx = - ay.by
b = (bx , b y )
ay
ax
=−
bx
by
∴
m r1 = −
1
m r2
Dos rectas son perpendiculares sí y sólo sí sus pendientes son recíprocas y opuestas
- 41 -
Sistema de coordenadas en R3
El sistema de coordenadas en R3 consiste en 3
planos perpendiculares 2 a 2 (planos coordenados)
Las rectas de intersección entre cada uno de los
planos se denominan:
Eje x o de abscisas
Eje y o de ordenadas
Eje z o de cotas
El punto o de intersección de las tres rectas es el
denomina origen de coordenadas.
Las intersecciones de estos planos coordenados dividen al espacio en 8 partes
denominadas octantes. Por convención, de denomina primer octante al espacio determinado
por los ejes x, y, z de valores positivos.
Coordenadas de un punto en el espacio
Un punto se puede ubicar en el espacio a partir de su referencia con la posición del punto
sobre los planos coordenados
z0
plzy
z0 = d(P,plxy )
plxz
P
x 0 = d(P,plyz )
y0
y0 = d(P,plxz )
x0
plxy
Vectores en R3 – Enfoque geométrico
Dado el punto P0 (x0,y0,z0), un vector en R3 es
una terna ordenada de números reales donde:
x0 1era componente del vector
y0 2da componente del vector
z0 3era componente del vector
- 42 -
Todas las propiedades vistas para vectores en R2 son válidas en R3.
Expresión cartesiana de un vector en R3
P(u , u , u )
1 2 3
u = OP = (u , u , u )
1 2 3
u = (u ,u ,u ) = (u ,0,0) + (0,u ,0) + (0,0,u )
1 2 3
1
2
3
(u ,u ,u ) = u (1,0,0) + u (0,1,0) + u (0,0,1)
1 2 3
1
2
3
(u ,u ,u ) = u i + u j + u k
1 2 3
1
2
3
Donde i , j , k son vectores de módulo 1 llamados versores fundamentales y apuntan en el
sentido positivo de las x , y, z respectivamente.
Operaciones con vectores
Sean u = ( u1 , u 2 , u 3 ) y v = ( v1 , v2 , v3 ) entonces:
Igualdad de vectores:
u=v ⇔
Módulo:
u1 = v 1 , u 2 = v 2 , u 3 = v 3
2
2
2
u = u1 + u 2 + u 3
Adición
u + v = (u1 + v 1 , u2 + v 2 , u3 + v 3 )
Sustracción
u − v = (u1 − v 1 , u 2 − v 2 , u3 − v 3 )
Producto de un escalar por un vector
k ∈R
k.u = (k.u1 , k.u 2 , k.u3 )
Nota:
k.u || u
Producto escalar o producto punto
c) Definición cartesiana del producto escalar
u .v = u1 .v1 + u 2 .v2 + u 3 .v3
- 43 -
d) Interpretación geométrica del producto escalar
u .v = u . v . cos uv
Criterio de Perpendicularidad
u ⊥ v ⇔ u .v = 0
Condición de Paralelismo
u
u
u
u || v ⇔ 1 = 2 = 3
v1 v 2 v 3
Producto vectorial o producto cruz
El producto vectorial es una operación binaria entre dos vectores de un espacio euclídeo
tridimensional que da como resultado un vector ortogonal a los dos vectores originales. Con
frecuencia se lo denomina también producto cruz (pues se lo denota mediante el símbolo ×)
En los textos, para evitar confusiones con la letra x (equis), es frecuente denotar el producto
v.
vectorial mediante u
∧
Dados dos vectores u y v, el producto vectorial de u ∧ v, da
como resultado el vector c, simultáneamente perpendicular a
ambos.
Si el producto vectorial da como resultado 0 (cero) significa que
ambos vectores son paralelos.
Para definir este nuevo vector es necesario especificar su
módulo y dirección.
Cálculo del producto vectorial entre u y v
u
v
i
j
k
u ∧ v = ux u y uz =
vx vy vz
uy uz
vy vz
.i −
ux uz
vx vz
.j +
ux uy
vx vy
.k
= ( uy .v z − v y .uz ) .i − ( ux .v z − v x .uz ) .j + ( ux .v y − v x .uy ) .k
Ejemplo: Dados los vectores a ( 2, 0, 1) y b (1,-1, 3 ) calcular a ∧ b
a∧b=
0 1
2 1
2 0
.i −
.j +
.k = (1, − 5 , − 2 )
−1 3
1 3
1 −1
Puede verificarse fácilmente que este vector resultante es perpendicular a los vectores a y b,
efectuando el producto escalar y verificando que es nulo.
- 44 -
Módulo del vector resultante
La magnitud del producto vectorial se puede definir como:
Donde α define el ángulo entre los dos vectores.
u ∧ v = u . v .senα
Geométricamente el módulo del vector resultante del producto vectorial define el área de un
paralelogramo con lados u y v .
O sea, dado el paralelogramo de lados u y v , su área estará definida por: Área = u ∧ v
u
α
v
Ángulo determinado por dos vectores
Siendo α el ángulo que forman los vectores u y v , tendremos que:
cos α =
u1.v1 + u 2 .v 2 + u 3 .v3
u.v
∴
α = arccos (
u1 . v 1 + u 2 . v 2 + u 3 .v 3
)
u.v
Componentes de un vector
→
Dados los puntos A(x1,y1,z1) y B(x2,y2,z2), las componentes de un vector AB se pueden
obtener restando a las coordenadas del extremo las coordenadas del origen
→
AB = (x 2 − x1, y 2 − y1, z 2 - z1 )
Distancia entre dos puntos
Dados los puntos A(x1,y1,z1) y B(x2,y2,z2), la distancia entre los dos puntos se puede obtener
como:
→
→
d(A,B) = AB = BA = (x 2 − x1,y 2 − y1,z2 - z1) = (x 2 − x1)2 + (y 2 − y1)2 + (z2 − z1)2
Ecuación de la recta en R3
1) Con vector director y punto
a) Ecuación vectorial
Para obtener la ecuación vectorial de la recta, no es suficiente considerar la dirección de la
recta mediante un vector, porque con esa misma dirección existen infinitas rectas.
- 45 -
Es necesario además, saber por dónde debe
pasar ésta, es decir un punto determinado
dentro del plano.
Así tendremos:
P0 (x 0 , y 0 , z 0 ) ∈ r
a = (a x , a y , a z ) a || r
r
donde a se denomina
vector director de la recta o vector asociado.
Para obtener la ecuación vectorial de la recta, se debe considerar otro punto genérico
→
→
→
P(x, y, z) de la misma. Aplicando la regla del polígono: OP = OP0 + P0P donde
→
→
PP0 = t a t ∈ R reemplazando
→
→
∴
→
OP = OP0 + t a
(x, y, z) = (x 0 , y 0 , z 0 ) + t(a x , a y , a z )
b) Ecuaciones paramétricas de la recta
Partiendo de la ecuación vectorial y operando en el segundo miembro obtendremos:
(x, y, z) = (x 0 , y 0 , z 0 ) + t(a x ,a y , a z )
(x, y, z) = (x 0 + ta x , y 0 + ta y , z 0 + ta z )
x = x 0 + ta x
y = y 0 + ta y
z = z 0 + ta z
Donde el número real t se denomina parámetro
c) Ecuación simétrica de la recta
Despejando t en las ecuaciones anteriores e igualando
x = x 0 + ta x
Si ax ≠ 0 , ay ≠ 0 y az ≠ 0
y = y 0 + ta y
z = z 0 + ta z
t =
t =
z − z0
az
resulta
t=
x − x0
ax
y − y0
ay
∴
x − x0
y − y0
z − z0
=
=
ax
ay
az
2) Con dos puntos
Es posible determinar la ecuación de una recta en el espacio, conociendo dos puntos que
pertenecen a la recta, ya que por éstos solamente puede pasar una sola recta.
- 46 -
P1
Datos
P0 (x 0 , y 0 , z 0 )

P1(x1, y1, z1 )
P0 ∈ r
P1 ∈ r
El vector director de la recta es el vector
P0P1 = (x1 - x 0 , y1 - y 0 , z1 - z0 )
P0
r
Así resultan:
a) Ecuación vectorial de la recta
(x, y, z) = (x 0 , y 0 , z 0 ) + t P1P0
(x, y, z) = (x 0 , y 0 , z 0 ) + t (x 1 - x 0 , y 1 - y 0 , z 1 - z 0 )
b) Ecuaciones paramétricas cartesianas de la recta
Partiendo de la ecuación vectorial y operando en el segundo miembro obtendremos:
x = x 0 + t (x1 - x 0 )
y = y 0 + t (y1 - y 0 )
Donde el número real t se denomina parámetro
z = z 0 + t (z1 - z 0 )
c) Ecuación simétrica de la recta
Despejando t en las ecuaciones anteriores
x − x0
y − y0
z − z0
=
=
x 1 - x 0 y 1 - y 0 z1 - z 0
Con x1 ≠ x0 , y1 ≠ y0 y z1 ≠ z0
Recta paralela a un plano coordenado
Es posible obtener las diferentes ecuaciones de las rectas paralelas a los planos
coordenados, de acuerdo al caso de paralelismo planteado.
Así, tendremos que:
1) r || plano xy ⇒ vector director a = (a x ,a y ,0)
2) r || plano xz ⇒ vector director a = (a x ,0, a z )
3) r || plano yz ⇒ vector director a = (0,a y , a z )
a) Ecuación vectorial
1) r || plano xy (x, y, z) = (x 0 , y 0 , z 0 ) + t(a x , a y ,0)
- 47 -
2) r || plano xz (x, y, z) = (x 0 , y 0 , z 0 ) + t(a x ,0, a z )
3) r || plano yz (x, y, z) = (x 0 , y 0 , z 0 ) + t(0, a y , a z )
b) Ecuaciones paramétricas
x = x 0 + ta x
1) r || plano xy 
y = y 0 + ta y

z = z 0
x = x 0 + ta x
2) r || plano xz 
y = y 0
z = z + ta
0
z

x = x 0 + ta x
3) r || plano yz 
y = y 0
z = z + ta
0
z

c) Ecuaciones simétricas
1) r || plano xy
2) r || plano xz
3) r || plano yz
x − x0 y − y0
=
ax
ay
; z = z0
x − x0 z − z0
=
ax
az
; y = y0
y − y0 z − z0
=
ay
az
; x = x0
Con a x ≠ 0 y a y ≠ 0
Con a x ≠ 0 y a z ≠ 0
Con a y ≠ 0 y a z ≠ 0
Recta paralela a un eje coordenado
1) r || eje z
y P0(x0,y0,z0) ∈ R
⇒
r || pl yz ⇒ x=x0
r || pl xz ⇒ y=y0
- 48 -
 x = x0
 y = y0
Ecuación de la recta r 
⇒
2) r || eje x
y P0(x0,y0,z0) ∈ R
r || pl xz ⇒ y=y0
r || pl xy ⇒ z=z0
 y = y0
 z = z0
Ecuación de la recta r 
⇒
3) r || eje y
y P0(x0,y0,z0) ∈ R
r || pl yz ⇒ x=x0
r || pl xy ⇒ z=z0
 x = x0
 z = z0
Ecuación de la recta r 
Ecuaciones de los ejes coordenados
y = 0
Eje x 
z = 0
x = 0
Eje y 
z = 0
x = 0
Eje z 
y = 0
Paralelismo
r1
r2
a = (a x , a y , a z )
b = (b x , b y , b z )
r1 || r2 ⇔ a || b
Dos rectas son paralelas sí y sólo sí, sus
respectivos vectores directores son paralelos
Perpendicularidad
r1
r2
r1 ⊥ r2
⇔
a⊥b
o bien
a = (a x , a y , a z )
b = (b x , b y , b z )
r1 ⊥ r2
- 49 -
⇔
a .b = 0
Nota: Observamos que en R3, las perpendiculares a una recta r que pasan por un punto P
son infinitas.
ECUACIONES DEL PLANO
Del mismo modo que lo visto anteriormente con
respecto a la recta, se puede proceder para hallar
la ecuación del plano que se satisfaga para los
infinitos puntos pertenecientes a él.
Un vector está asociado a un plano cuando dicho vector es ortogonal o normal al mismo.
Este vector asociado se denomina Vector Director.
P0 (x0 ,y 0 ,z0 ) ∈ π
n = (nx ,ny ,nz ) asociado
Datos  Siendo
n⊥π
n ≠ 0, n ≠ (0,0,0)
P(x, y, z) ∈ π
→
n ⊥ P0P ⇒
Desarrollando tendremos que:
(nx, ny, nz) (x - x0,y - y0,z - z0) = 0
nx (x - x0) + ny (y - y0) + nz(z - z0) = 0
nx x + ny y + nz z + (-nxx0-nyy0-nzz0) = 0
A
B
C
D
COMPONENTES DEL VECTOR DIRECTOR DEL PLANO
- 50 -
→
n • P0P = 0
Ecuación general o implícita del Plano donde
A, B y C no son simultáneamente nulos
Ax + By + Cz + D = 0
Planos Coordenados
z
plxy es un plano cuya ecuación es Z=0
plxz es un plano cuya ecuación es Y=0
plzy
plxz
plzy es un plano cuya ecuación es X=0
plxy
Intersección de un plano con los planos coordenados: TRAZAS
By + Cz + D = 0 ∧ X = 0
Ax + Cz + D = 0 ∧ Y = 0
π → Ax + By + Cz + D = 0
Ax + By + D = 0 ∧ Z = 0
Dado un plano π definido por la ecuación general del plano Ax+By+Cz+D=0, si hallamos la
intersección de cada uno de los planos coordenados con el plano π , se obtienen las
- 51 -
ecuaciones indicadas en el dibujo anterior, denominadas trazas del plano π sobre cada
plano coordenado.
Intersección de un plano con los ejes coordenados: PUNTOS
c P3 (0,0, c)
π → Ax + By + Cz + D = 0
b
a
P2 (a,0,0)
P1 (0, b,0)
Dado un plano π definido por la ecuación general del plano Ax+By+Cz+D=0, si hallamos la
intersección de cada uno de los ejes coordenados con el plano π , se obtienen los puntos a,
b, c indicados en el dibujo anterior. De esta condición se puede obtener la ecuación
segmentaria del plano que se indica a continuación: x y z
+ + =1
a b c
Donde a, b y c son los puntos de intersección con cada eje coordenado
Posiciones particulares del plano
a) Plano que pasa por el origen
- 52 -
π → Ax + By + Cz = 0 ∧ D = 0
pasa por el punto (0,0,0)
b) Plano paralelo a un eje coordenado
Sea π un plano paralelo a uno de los ejes
coordenados, supongamos en este caso al
y (ordenadas) podemos afirmar que, si π
es paralelo al eje de ordenadas, su vector
asociado n es perpendicular al versor j .
Entonces
n• j = 0
(nx, ny, nz) (0,1,0) =0
nx 0 + ny 1 + nz 0 =0
ny =0
Reemplazando ny en la ecuación general del plano resulta
π → Ax + Cz + D = 0
x z
+ =1
a c
Del mismo modo es posible analizar los casos donde el plano sea paralelo a los otros ejes
teniendo:
π → By + Cz + D = 0
y z
+ =1
b c
π → Ax + By + D = 0
x y
+ =1
a b
- 53 -
si el plano es paralelo al eje X
si el plano es paralelo al eje Z
c) Plano que incluye a un eje coordenado
Sea π un plano que incluye a un eje coordenado, en este caso al eje X, el plano π
contendrá el origen de coordenadas, y será paralelo al eje X, por lo tanto, su vector
asociado n será perpendicular al versor i .
Entonces
n• i = 0
(nx, ny, nz) (1,0,0) =0
nx 1 + ny 0 + nz 0 =0
nx =0
Reemplazando nx en la ecuación general del
plano y teniendo en cuenta que D=0 por
pertenecer el origen de coordenadas al plano
π , resulta:
π → By + Cz = 0
y=−
C
z
B
Analizando del mismo modo los casos para los que el plano incluye los otros ejes
cartesianos. Tendremos
π → Ax + Cz = 0
x=−
C
z
A
si el plano incluye al eje y
π → Ax + By = 0
x=−
B
y
A
si el plano incluye al eje Z
d) Plano paralelo a un plano coordenado
D
z=−
C
y=−
D
B
Sea π un plano paralelo a uno de los planos
coordenados, supongamos en este caso al
plano xy (plano rojo en la figura) podemos
decir que π es paralelo al eje X y paralelo al
Y. Por darse esta condición, resulta que nx=0
y ny=0. Reemplazando estos valores en la
ecuación general del plano podemos decir que
π → Cz + D = 0
- 54 -
z=−
D
C
Del mismo modo es posible analizar los casos para los que el plano sea paralelo a los otros
planos obteniendo
π → By + D = 0
π → Ax + D = 0
y=−
D
B
si el plano es paralelo al plano XZ
x=−
D
A
si el plano es paralelo al plano YZ
Condición de paralelismo entre planos
→
n
α
→
n'
β
Sean α y β dos planos paralelos de ecuaciones
α → Ax + By + Cz + D = 0
β → A' x + B' y + C' z + D' = 0
Sus vectores asociados también serán paralelos, por lo que sus componentes homólogas
serán proporcionales, tendremos entonces:
nx n y nz
=
=
n'x n'y n'z
A B C
= =
A' B' C'
Condición de perpendicularidad entre planos
n'
Sean α y β dos planos perpendiculares de ecuaciones
α
n
α → Ax + By + Cz + D = 0
β
β → A' x + B' y + C' z + D' = 0
- 55 -
Sus vectores asociados también serán perpendiculares, por lo que el producto escalar de
los mismos deberá ser nulo. Tendremos entonces:
→
n •n' = 0
nxn'x +nyn'y +nzn'z = 0
A.A' + B.B' + C.C' = 0
Rectas y planos en el espacio, definen envolventes según su posición relativa:
Arq. Mies Van der Rohe
Arq. Wolf D. Prix – Ópera de Munich
Studio Arquitectonica
Arq. Rem Koolhas – Biblioteca Pública, EEUU
- 56 -
NOTAS SOBRE CURVAS CÓNICAS
MATEMÁTICA PARA ARQUITECTOS
“El gran estilo nace cuando lo bello
obtiene la victoria sobre lo enorme”
Friedrich W. Nietzsche
- 57 -
Llamamos superficie cónica de revolución a la superficie
generada por una línea recta llamada generatriz que gira
alrededor de un eje, manteniendo un punto fijo sobre dicho eje.
Se denominan cónicas a las curvas que resultan de seccionar
una superficie cónica circular recta, con un plano.
Sea S la superficie cónica circular recta y α el plano, puede ocurrir
que:
a) Cuando α no es perpendicular al eje de la superficie y
corta a todas las generatrices, la curva obtenida es una
elipse.
Si α además pasa por el vértice la intersección es un punto.
CASO PARTICULAR:
Si el plano α es perpendicular al eje de revolución de la
superficie cónica, se obtiene una
circunferencia.
b) Cuando el plano α es paralelo a una sóla generatriz de la
superficie cónica, la curva obtenida es una parábola. Si α
además pasa por el vértice, la intersección es una recta.
c) Cuando el plano α es paralelo a dos generatrices, la curva
obtenida es una hipérbola. Si α además pasa por el vértice, la
intersección son dos rectas.
- 58 -
Las cónicas responden a una ecuación de segundo grado en x e y del tipo:
Ax²+By²+Cxy+Dx+Ey+F=0
Que puede presentarse incompleta. (Con A, B y C no simultáneamente nulos)
CIRCUNFERENCIA
Definición:
“Es el lugar geométrico de los puntos del plano que equidistan de otro llamado centro; esa
distancia se llama radio.”
El punto fijo se denomina centro de la circunferencia y la distancia de cualquier punto de la
circunferencia al centro de la misma se denomina radio.
Para hallar la ecuación de una circunferencia en un centro C (h, k) y radio r podemos
proceder así:
Sea P ( x ; y) un punto cualquiera de la
P(x;y)
circunferencia; en el CPR resulta :
r
( x − h)2 + ( y − k )2 = r 2
(1)
1
la
ecuación
cartesiana
de
la
circunferencia de centro C(h,k) y radio r
.
y-k
C(h;k) x-h R
1
O (0;0)
ECUACION GENERAL DESARROLLADA
Partiendo de la ecuación (1), efectuamos las operaciones indicadas y ordenamos
convenientemente:
x 2 + y 2 − 2hx − 2ky + h 2 + k 2 − r 2 = 0
si hacemos A = -2h ,
B = -2k ,
C = h2 + k2 - r2 tendremos :
x2 + y2 + A x + B y + C = 0
Si la ecuación esta dada en esta forma, podemos calcular las coordenadas del centro y su
radio, ya que:
A = −2h ⇒ h = −
A
2
B = −2k ⇒ k = −
B
2
- 59 -
C = h2 + k 2 − r 2 ⇒ r = h2 + k 2 − C
Puede ocurrir que:
h2 + k 2 − C = 0 ⇒ r = 0 es un punto
h2 + k 2 − C < 0 ⇒ r no es real
Como caso particular de las circunferencias, podemos considerar las que tienen centro en el
x 2 + y 2 = r 2 la ecuación
origen de coordenadas y radio r. Entonces, h = k = 0 , siendo
canónica de la circunferencia.
•
Ejemplos:
(0,00; 5,00)
1. Encontrar la ecuación de la
circunferencia de centro (0,0) y que
pasa por (3,-4)
1
Reemplazando en la ecuación
canónica x 2 + y 2 = r 2 , obtenemos
O
1
(-5,00; 0,00)
(5,00; 0,00)
2
3 2 + ( −4 ) = r 2 , ⇒ r 2 = 25 , por lo
tanto la ecuación buscada es
x 2 + y 2 = 25
(3,00; -4,00)
(0,00; -5,00)
2. Hallar
la
ecuación
de
la
circunferencia de centro C(1;-2) y
radio 4
Reemplazando en la ecuación
cartesiana cuyo centro es (h;k),
obtenemos:
(1,00; 2,00)
1
O
1
r
(-3,00; -2,00)
(1;-2)
(5,00; -2,00)
( x − 1) 2 + ( y + 2 ) 2 = 16
(1,00; -6,00)
- 60 -
3. Graficar la
ecuación
circunferencia
de
(-2,00; 6,00)
x 2 + y 2 + 4x − 6y + 4 = 0 ,
indicando las
coordenadas
del centro y radio
C (-2;3)
(-5,00; 3,00)
Según la ecuación desarrollada
de la circunferencia,
(1,00; 3,00)
r
4=-2h ⇒ h=-2
1
O
(-2,00; 0,00)
-6=-2k ⇒ k=3
1
4 = h2 + k 2 – r 2 ⇒ 4 = 4 + 9 - r 2
⇒ r2 = 9
C(-2;3), radio 3
ELIPSE
La elipse es el lugar geométrico de los puntos del plano cuya suma de distancias a dos
puntos fijos llamados focos es constante e igual a 2a (esta distancia es mayor que la
distancia entre los focos)
B
P
1
A'
O
F'
A
1
F
B'
P pertenece a la elipse si y solo si: PF + PF´ = 2a
• Descripción:
AA ' = 2a diámetro focal o mayor
B
a
A'
F'
c
b1
O
BB ' = 2b diámetro menor
A
1
F
B'
AA ' ⊥ BB' trazada por el origen
FF' = 2c es la distancia focal
A, A ',B yB ' son los vértices
a
- 61 -
Se llama excentricidad ‘e’ al cociente entre la semidistancia focal y el semidiámetro mayor
e=
c
; siempre e < 1 , pues c < a
a
Para cierto valor fijo de ‘a’, si ‘c’ decrece también decrece ‘e’, la elipse tiende a una
circunferencia. Si ‘c’ crece, también crece ‘e’, y la elipse se aplana.
• Relación entre semidiámetro mayor ‘a’ semidiámetro menor ‘b’ y semidistancia focal ‘c’
En la figura anterior,
de (1) y (2)
B ∈ a la elipse, por definición, es: BF + BF' = 2a
(1)
B ∈ a la mediatriz de FF' ⇒ BF = BF'
(2)
BF + BF' = 2a ⇒ 2 BF = 2a ⇒ BF = a
2
∆
en BOF rectángulo en O:
2
BF = BO + OF
2
a2 = b2 + c 2
Ecuación canónica de una elipse
Sea una elipse con centro en el origen de coordenadas y con el eje focal coincidente con el
eje ´x´, su ecuación canónica
será:
(0;b)
2
y
2
x + y =1
a2 b2
(-a;0)
O
F' (-c;0)
P
1
1
(a;0)
x
F (c;0)
(0;-b)
A (o;a)
F (0;c)
Si los focos se encontraran sobre el eje ‘y’, la ecuación es
P
2
x2 + y = 1
b2 a2
1
B (-b;0)
O
1
F' (0;-c)
- 62 -
B' (b;0)
ELIPSES TRASLADADAS:
B'
• Si el eje focal es paralelo al eje ‘x’ y
el centro es C(h,k) , de la ecuación
A
2
x 2 + y = 1, pasamos a
a2 b2
( x − h)2 + ( y − k )2
a
2
b
2
F
F'
C (h;k)
1
=1
O
1
B
A'
F'
•
Si el eje focal es paralelo al eje ‘y’ y el centro es C(h,k) , de
2
2
2
x 2 + y = 1, pasamos a ( x − h ) + ( y − k ) = 1
la ecuación
b2 a2
b2
a2
B
B'
C (h;k)
Obsérvese que en las ecuaciones siempre a > b . La
circunferencia, es un caso particular de elipse cuyos
semidiámetros a y b, son iguales.
1
O
1
F
A
Anfiteatro de Pompeya
- 63 -
A'
HIPÉRBOLA
La hipérbola es el lugar geométrico de los todos los puntos del plano tales que la
diferencia de sus distancias, en valor absoluto, a dos puntos fijos llamados focos es
constante. Esa constante la simbolizamos 2a (esta distancia es menor que la distancia entre
los focos)
P
F
P
y
pertenece
solo
a
A
a
1
O
1
F'
A'
la
si:
hipérbola si
PF − PF' = 2a
•
Descripción:
AA ' = 2a diámetro real
r
F
A
c
FF' = 2c es la distancia focal
1
BB ' = 2b diámetro imaginario
B' 1
b O
a
1 A' F'
AA ' ⊥ BB' trazada por el origen
A, A ',B yB ' son los vértices
r1 y r2 son las asíntotas
B
r2
Ecuación canónica de una hipérbola:
Para obtener la ecuación canónica de la hipérbola, el eje focal y el eje imaginario deben
estar incluidos en los ejes coordenados, por lo tanto, su centro coincide con el origen de
coordenadas.
•
Si el eje focal coincide con el eje de
abscisas y el eje imaginario con el
eje de ordenadas, la ecuación es:
2
2
x − y =1
a2 b2
r
F
(1)
A
c
1
B' 1
b O
a
1 A' F'
B
r2
- 64 -
•
Si el eje focal coincide con el eje de ordenadas ‘y’,
y el eje imaginario con el eje de abscisas, la
ecuación es:
y
r1
F'
2
2
− x =1
2
a
b2
A'
1
(2)
1
B'
B
A
F
r2
Propiedad Pitagórica:
r1
F
A
En la hipérbola:
B' 1
c
b O
a
FF' = 2c
1 A' F'
AA' = 2a
y
BB' = 2b
y se cumple:
c 2 = a 2 + b2
B
r2
Asíntotas de la hipérbola:
Dada la hipérbola, existen dos rectas tales que a medida que un punto de la curva se aleja
indefinidamente del origen, la distancia de ese punto a dichas rectas decrece
continuamente, es decir, tiende a cero.
Dichas rectas se llaman asíntotas de la hipérbola, y son las que incluyen las diagonales del
rectángulo de lado ‘2a’ y ‘2b’.
Para encontrar las ecuaciones explícitas de las asíntotas, tendremos en cuenta que son dos
rectas que pasan por el origen y de las que se conoce la pendiente.
b
x
a
b
r2 → y = − x
a
r1 → y =
a. En la ecuación (1)
- 65 -
a
x
b
a
r2 → y = − x
b
r1 → y =
b. En la ecuación (2)
Las ecuaciones implícitas de las asíntotas en el caso (1) son:
r1 → bx + ay = 0
r2 → bx − ay = 0
Sabiendo que la ecuación de la hipérbola, para este caso, es
2
x 2 − y = 1, las ecuaciones
a2 b2
de las asíntotas pueden obtenerse anulando el segundo miembro de la ecuación canónica y
factorizando el primero.
2
x2 − y = 0
a2 b2
b2x 2 − a2y 2 = 0
(bx + ay ) = 0
(bx + ay )(bx − ay ) = 0
(bx − ay ) = 0
HIPÉRBOLAS TRASLADADAS:
• Si el eje focal es paralelo al eje
x’, de la ecuación
2
x 2 − y = 1, pasamos a:
a2 b2
r2
F
A
A'
1
( x − h)2 − ( y − k )2
a2
b2
1
O (0;0)
=1
- 66 -
r1
B'
C (h;k)
B
F'
•
Si el eje focal es paralelo al eje ‘y’,
de la ecuación
a
y2
2
− x = 1, pasamos
a2 b2
F'
A'
B
( y − k )2 − ( x − h)2
a2
b2
C (h;k)
1
=1
1
B'
A
F
HIPÉRBOLA EQUILÁTERA:
Se llama hipérbola equilátera a aquella que tiene iguales diámetros real e imaginario, o sea
que a = b
En el caso (1), donde el eje real es ‘x’, se presenta así
En el caso (2), de eje real ‘y’, será
2
x 2 − y = 1, o bien x 2 − y 2 = a2
a2 a2
y2
2
− x = 1 , o y 2 − x 2 = a2
a2 b2
La semidistancia focal es c = a2 + b2 =
2a2 = a 2
Las ecuaciones de las asíntotas son y = ± x , perpendiculares entre sí e incluyen a las
bisectrices del 1º y 2º cuadrante.
Arq. Pedro Fisac.
Iglesia San Pedro Mártir.
Madrid
- 67 -
PARÁBOLA
La parábola es el lugar geométrico de
los puntos del plano que equidistan
de un punto fijo llamado foco y de una
recta fija llamada directriz.
P
Sea la directriz, el foco ‘F’ y un punto
‘P’ de la parábola, por definición es:
F
PF = PQ
1
O (0;0)
La perpendicular a la directriz trazada
por el foco es el eje de la parábola y
es su eje de simetría. El eje corta a la
directriz en el punto ‘A’, llamamos
1
Directriz
parámetro al segmento AF
Ecuación de la parábola:
Supongamos
que
el
foco
esté
p
2


situado en el punto  0,  y la
directriz es la recta
P (x;y)
F (0; p/2)
p
y = − , el
2
1
vértice estará en su punto medio
(0,0). Si tomamos un punto
cualquiera P(x,y) de la parábola y un


punto Q  x; −
1
Vértice O (0;0)
p
perteneciente a la
2 
Directriz y = -p/2
Q (x;-p/2)
recta directriz, según la definición,
debe de cumplirse que :
PF = PQ
→
2
p
x +  y −  =
2

2
2
p
p
x 2 +  y −  =  y + 
2
2


Elevando ambos miembros al cuadrado
Desarrollando los binomios
y+p

2 

x 2 + y 2 − 2y
- 68 -
2
2
p p
p
p
+   = y 2 + 2y +  
2 2
2 2
2
2
Simplificamos
x2 + y2 − 2y
2
p p
p
p
+   = y 2 + 2 y +  
2 2
2 2
2
y obtenemos la ecuación: x 2 = 2py donde ∀x : x 2 ≥ 0 ⇒ 2py ≥ 0 ⇒ y ≥ 0 , es decir sólo
hay puntos de la curva para valores no negativos de ‘y’ ; es cóncava hacia arriba.
Con un razonamiento análogo al anterior, podemos
deducir la ecuación de una parábola cuyo eje de
simetría es el ‘y’, pero con concavidad hacia abajo
Directriz y = p/2
1
V (0;0)
1
x 2 = −2py
F (0;-p/2)
Donde ∀x : x 2 ≥ 0 ⇒ −2py ≥ 0 ⇒ y ≤ 0
Las ecuaciones de la parábola de eje de simetría ‘x’, vértice (0,0), resultan:
a.
que
y2 = 2px
b.
∀y : y2 ≥ 0 ⇒ 2px ≥ 0 ⇒ x ≥ 0
y 2 = −2px
teniendo en cuenta
∀y : y 2 ≥ 0 ⇒ −2px ≥ 0 ⇒ x ≤ 0
Dir x = p/2
Dir x=-p/2
1
1
V (0;0)
1
F(p/2;0)
F (-p/2;0)
Ecuaciones de la parábola traslada:
•
Si la parábola tiene vértice (h,k) y eje paralelo al eje ‘y’
- 69 -
1
V (0;0)
De la ecuación x 2 = 2py
De la ecuación x 2 = −2py
Obtenemos ( x − h )2 =2p ( y − k )
obtenemos
( x − h )2 = − 2p ( y − k )
1
h
1
O (0;0)
Directriz
F
V (h;k)
k
k
V (h;k)
1
1
O (0;0)
•
Directriz
F
h
Si la parábola tiene vértice (h,k) y eje paralelo al eje ‘x’
De la ecuación y 2 = 2px
De la ecuación y 2 = −2px
Obtenemos ( y − k )2 =2p ( x − h )
obtenemos ( y − k ) = − 2p ( x − h )
2
Directriz
Directriz
F
k
F
V (h;k)
1
1
O (0;0)
k
1
h
h
- 70 -
1
O (0;0)
Arq. W. Eyre Gatesghead Millennium. Inglaterra
Arq. Pier Luigi Nervi. Maqueta
- 71 -