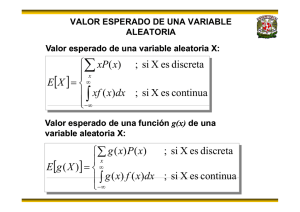
variable aleatoria

03 – Variables aleatorias y
distribuciones de probabilidad
Contenido
●
●
Diego Andrés Alvarez Marín
Profesor Asistente
Universidad Nacional de Colombia
Sede Manizales
●
●
1
Variable aleatoria
Sea Ω un espacio muestral. Una función
Nota: la definición real es en verdad algo más complicada. Ver:
http://en.wikipedia.org/wiki/Random_variable#Formal_definition
Variables aleatorias continuas: función de densidad y de
distribución
Características de las variables aleatorias: valor esperado,
varianza
Aplicación práctica, representaciones
2
●
●
●
se conoce como variable aleatoria (random
variable en inglés)
Variables aleatorias discretas: función de probabilidad y
de distribución
●
La variable aleatoria transforma los resultados
del espacio muestral en cantidades numéricas.
La letra mayúscula X denota la función (la
variable aleatoria).
La letra minúscula x denota el valor que toma
la variable aleatoria, es decir, x=X(ω)
Observe que una “variable” aleatoria NO es
una variable como tal sino que es una función
Lanzamientos de dos dados
X denota la suma de los resultados de las dos caras
Valor de la
variable
aleatoria
Resultado (ω)
(1,1)
(1,2),
(1,3),
(1,4),
(1,5),
(1,6),
(2,6),
(3,6),
(4,6),
(5,6),
(6,6)
(2,1)
(2,2),
(2,3),
(2,4),
(2,5),
(3,5),
(4,5),
(5,5),
(6,5)
(3,1)
(3,2),
(3,3),
(3,4),
(4,4),
(5,4),
(6,4)
(4,1)
(4,2), (5,1)
(4,3), (5,2), (6,1)
(5,3), (6,2)
(6,3)
Número de
x := X(ω) ocurrencias Probabilidad
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
5
4
3
2
1
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
∑ = 36
∑=1
●
●
Una variable aleatoria X es discreta si D tiene
una cardinalidad finita o infinita contable (es
decir si los elementos de D se pueden poner en
una correspondencia uno a uno con los
números naturales)
Una variable aleatoria X es continua si D tiene
una cardinalidad infinita no contable, es decir si
D está formado por intervalos de la recta real
Eventos definidos por la variable
aleatoria X:Ω→R
Descripción probabilista de las
variables aleatorias
●
●
Función de Masa de Probabilidades
Definición matemática
Las variables aleatorias discretas se describen
mediante:
–
Función de Masa de Probabilidades (FMP)
–
Función de Distribución de Acumulada (FDA)
Las variables aleatorias continuas se
describen mediante:
–
Función de Densidad de Probabilidades (FDP)
–
Función de Distribución de Acumulada (FDA)
Función de Masa de Probabilidades
Una función de masa de probabilidades (FMP)
es una funcion que dice la probabilidad que una
variable aleatoria discreta tome exactamente un
valor.
Una FMP. Observe que todos los
valores de esta función son nonegativos y suman 1.
Una FMP de un dado equilibrado.
Todos los números en el dado
tienen igual probabilidad de
aparecer.
Graficando FMPs en MATLAB
Propiedades de la FMP
Las FMP deben satisfacer las siguientes
propiedades:
La función Delta de Dirac
Representación de una FMP
utilizando Deltas de Dirac
Ejemplo
Para verificar la calidad de un lote de cilindros de
concreto, un ingeniero extrae al azar 3 muestras.
Suponiendo que la probabilidad que el cilindro no
cumpla las especificaciones es del 10%, cual es la
probabilidad que:
●
a) los tres cilindros cumplan con las especificaciones
●
b) sólo dos cilindros cumplan con las espeficicaciones
●
c) sólo un cilindro cumpla con las espeficicaciones
●
s – cilindro que cumple con las especificaciones
n – cilindro que NO las cumple
P(s) = p
P(n) = 1-p
P[0 OK] = (n,n,n) = (1-p)(1-p)(1-p) = (1-p)3
P[1 OK] = (n,n,s)+(n,s,n)+(s,n,n) = 3(1-p)2p
P[2 OK] = (n,s,s)+(s,s,n)+(s,n,s) = 3p2(1-p)
P[3 OK] = (s,s,s) = p3
FMP binomial
d) ninguno de los cilindros cumpla con las
especificaciones
En el caso del ejemplo p = 0.90, siendo la FMP:
3
3
P[0 OK] = (1-p) = (0.1) = 0.001
P[1 OK] = 3(1-p)2p = 3 (0.1)2 x 0.9 = 0.027
P[2 OK] = 3p2(1-p) = 3 (0.9)2 x 0.1 = 0.243
P[3 OK] = p3 = (0.9)3 = 0.729
En la práctica de control de calidad, el ingeniero
debe tomar la decisión acerca de si el material
se encuentra dentro de las especificaciones o no
basado en una observación de dos muestras
malas en una muestra de tamaño tres.
Suponiendo que el material es satisfactorio, la
probabilidad de tal suceso es muy pequeña
(2,7%), y por lo tanto, el ingeniero decidirá
usualmente que el material no cumple con las
especificaciones.
Ejemplo lanzamiento de una
moneda
Ejemplo
¿Cuántas veces se debe lanzar una moneda para obtener caras?
1–C
P(C)
= 0.5
2 – SC
P(SC)
= 0.52
3 – SSC
P(SSC)
= 0.53
4 – SSSC
P(SSSC)
= 0.54
...
... n-1 veces
n – S...SSC
P(S...SSC) = 0.5n
se extiende
hasta el
infinito
http://en.wikipedia.org/wiki/Geometric_series
Función de Densidad de Probabilidades (FDP)
Intelligence quotient
IQ μ=100, σ=15
Motivación
●
●
Interpretación de la FDP
●
●
La FDP fX del caso continuo se debe entender
de forma diferente a la FMP pX del caso
discreto:
–
Con las FMPs, la probabilidad que x tome un valor
específico puede ser diferente de cero.
–
Con las FDPs, la probabilidad que x tome un valor
específico x es cero.
Por lo tanto, la FDP no representa la
probabilidad que X=x. Mas bien proporciona un
medio para determinar la probabilidad de un
intervalo a≤X≤b.
Las FDPs se pueden entender como el límite
de un histograma cuando el ancho de cada
subintervalo tiende a cero.
Cuando la altura de una persona es 172 cm, es
lógico entender como [171.5 cm, 172.5 cm]; por
lo tanto, en el caso continuo es más lógico
visualizar las probabilidades de intervalos que
de un punto en particular.
Interpretación de la FDP
●
El valor de fX(x) solo es una medida de la
densidad o intensidad de la probabilidad en el
punto x.
Interpretación de la FDP
●
Función de Distribución Acumulada
(FDA)
El valor de fX(x) solo es una medida de la
densidad o intensidad de la probabilidad en el
punto x.
más
frecuencia
Colas de la
FDP
menos
frecuencia
FDA de una función de
masa de probabilidades
(FMP)
Continuidad por la derecha y por la
izquierda
FDA de una función de
densidad de
probabilidades continua
FDA de una función de
densidad de
probabilidades que tiene
un componente continuo
y una parte discreta.
Función continua por
la derecha
Función continua por
la izquierda
Función de Distribución Acumulada
(FDA)
Función de Distribución Acumulada
(FDA)
FMP vs FDA
Ejemplo: FMP y FDA uniforme discreta
Ejemplo: FDA discreta (Poisson)
P(X≤k)
λ>0 representa el número esperado de ocurrencias
durante un intervalo dado de tiempo. Por la FDA del evento
que lleguen k clientes a un banco dado que en promedio
llegan λ=1, 4 y 10 clientes/minuto se muestra a
continuación:
k
FDP vs FDA
FDP vs FDA
Ejemplo
Continuación ejemplo
Función de distribución de
probabilidades empírica
Función de distribución de
probabilidades empírica
43
44
El comando disttool del toolbox de
estadística de MATLAB
Dicho comando es
extremadamente útil
para explorar la forma
de las FDPs y FDAs
45
Variables aleatorias mixtas
g(x)
Variables aleatorias mixtas
La variable aleatoria puede ser a la vez discreta y
continua, es decir asume valores puntuales con
una probabilidad diferente de cero, al igual que
valores por intervalos. Este es el caso de ensayo
de equipos, donde X es el tiempo de
funcionamiento
del
equipo,
existe
una
probabilidad de que el artículo no funcione del
todo, falla en el tiempo X = 0; ó también cuando Y
es la variable aleatoria que representa la demora
de un motorista al hacer un pare obligatorio,
existe una probabilidad de que no haya tráfico y
el motorista no tenga demora X = 0, sí tiene que
esperar, lo debe hacer por un tiempo continuo.
Variables aleatorias mixtas
Ejemplo 2:
variables
aleatorias
mixtas
FDP truncada
●
http://en.wikipedia.org/wiki/Truncated_distribution
FDP condicional
●
●
FDP de una función g(X)
Suponga que estamos interesados en la
distribución de la demanda o carga X dado que
sea mayor que algún valor de umbral x0.
HACER GRAFICO FDP truncada
FDP a partir de observaciones
●
Kernel smoothing methods (tambien llamado
ventanas de Parzen (Parzen windows). El
comando de MATLAB asociado es ksdensity.
Ver: http://en.wikipedia.org/wiki/Kernel_density_estimation
FDP a partir de observaciones
Valor esperado de una variable
aleatoria
Existen otro métodos basados en la utilización de
polinomios ortogonales de Legendre. Ver por
ejemplo:
El valor promedio de una variable aleatoria
después de un número grande de experimentos
es su valor esperado.
X.B. Li y F.Q. Gong (2009). A method for fitting
probability distributions to engineering properties
of rock masses using Legendre orthogonal
polynomials. Structural Safety. Volume 31, Issue
4, July 2009, Pages 335-343
Se dice valor esperado (expected value) o
también esperanza matemática (mathematical
expectation)
Applying the Gram-Schmidt process to the functions 1, x, x^2, ... on the
interval [-1,1] with the usual L^2 inner product gives the Legendre polynomials
Valor esperado de una variable aleatoria
Valor esperado de una variable aleatoria
Ver:
–
http://en.wikipedia.org/wiki/Riemann-Stieltjes_Integration
–
http://en.wikipedia.org/wiki/Cauchy_distribution
Ejemplo: valor esperado
Paradoja de San Petersburgo
http://en.wikipedia.org/wiki/St._Petersburg_paradox
El valor esperado no necesariamente toma un
valor que pudiera tomar la variable aleatoria.
Paradoja de San Petersburgo
http://en.wikipedia.org/wiki/St._Petersburg_paradox
Valor esperado VA uniforme continua
●
Valor esperado VA exponencial
Propiedades del valor esperado
Propiedades del valor esperado
Interpretación del valor esperado
Valor esperado de una constante:
●
●
●
Desigualdades:
●
El término “valor esperado” no
entenderse como el valor más probable.
debe
El valor esperado se debe entender como el
valor promedio que toma la variable aleatoria
después de efectuar muchos experimentos
independientemente.
El valor esperado se puede asociar al centro de
gravedad de la FDP.
Importancia práctica del valor
esperado
Valor esperado de una función g(X)
En un problema físico, en que un fenómeno tiene
como
modelo
una
variable
aleatoria,
generalmente el número más significativo que el
ingeniero puede obtener es el valor medio de esa
variable; es una medida de la tendencia central
de la variable y muchas veces, si se van a hacer
observaciones repetidas del fenómeno, del valor
alrededor del cual se pude esperar la dispersión.
La media muestral de muchas de tales
observaciones estará con alta probabilidad muy
cerca a la media de la variables aleatoria
fundamental.
Valor esperado de una función g(X)
●
Tenga en cuenta que
●
Otra propiedad del valor esperado es:
Ejemplo: valor esperado de g(X)
Esperanza condicional
Ejemplo 1 esperanza condicional
Ejemplo 2 esperanza condicional
Momentos de una variable aleatoria
Los momentos de una variable aleatoria X son los
valores esperados de ciertas funciones de X.
Estas forman una colección de medidas
descriptivas que pueden emplearse para
caracterizar la distribución de probabilidad de X y
especificarla si todos los momentos de X son
conocidos. A pesar de que los momentos de X
pueden definirse alrededor de cualquier punto de
referencia, generalmente se definen alrededor del
cero (momentos no centrales) o del valor
esperado de X (momentos centrales).
Momentos no centrales
Momentos centrales
Algunos momentos centrales
Media cuadrática VA uniforme
continua
Media cuadrática VA exponencial
Notas sobre los momentos
●
●
Tenga en cuenta que todas las proposiciones
anteriores con respecto a los momentos se
encuentra sujetas a la existencia de las sumas
o integrales que las definan.
El uso de los momentos de una variable
aleatoria para caracterizar a la FDA es útil
especialmente en un medio en el que el
experimentador conozca la FDA.
Varianza
Varianza
La varianza es una medida de la dispersión de
una variable aleatoria.
La varianza es una medida de la dispersión de
una variable aleatoria.
Relacionando la varianza con la
media y la media cuadrática
Un dado perfecto
Varianza FDP exponencial
Varianzas
Uniforme
Exponencial
Propiedades de la varianza
Notas sobre la varianza
Ley de la esperanza total
Si una distribución no tiene esperanza, como
ocurre con la de Cauchy, tampoco tiene varianza.
Existen otras distribuciones que, aun teniendo
esperanza, carecen de varianza. Un ejemplo de
ellas es la de Pareto cuando su índice k satisface
1 < k ≤ 2.
92
Coeficiente de variación (C.O.V.)
Ley de la varianza total
Es una medida normalizada de la dispersión,
utilizada en control de calidad. Está definida por:
Está definida para valores positivos de μ.
●
●
●
Es útil porque la desviación estándar se debe
entender siempre en contexto con la media. Como
no tiene dimensión, sirve para comparar
dispersiones de datos con medias diferentes
Es sensitiva a pequeños cambios en la media
cuando esta se acerca a cero, limitando su utilidad.
NOTA: No confundir con la covarianza
93
Coeficiente de asimetría (skewness)
g1 < 0 distribución asimétrica
negativamente
g1 > 0 distribución asimétrica
positivamente
Coeficiente de apuntalamiento
(curtosis)
Desigualdad de Chebyshev
Otras medidas de tendencia central
y dispersión
La media de una variable aleatoria es
generalmente la medida preferida de tendencia
central. Sin embargo, en algunas situaciones la
mediana y en menor grado la moda, pueden ser
mediadas de tendencia central mucho más
apropiadas. Por ejemplo, en distribuciones
unimodales cuya asimetría es grande, el valor
esperado de la variable aleatoria puede verse
afectado
por los valores extremos de la
distribución, mientras que la mediana no lo
estará.
Relación entre la media, la mediana
y la moda en distribuciones
unimodales
Mediana de una FMP/FDP
Cuantil de una FMP/FDP
Moda de una FMP/FDP
Algunos cuartiles:
- Percentil
q = 0.01
- Decil
q = 0.10
- Cuartil
q = 0.25
- Mediana
q = 0.50
101
Otras medidas de dispersión
103
102