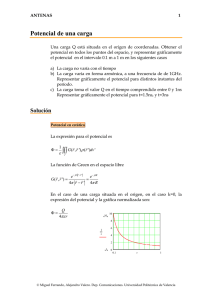
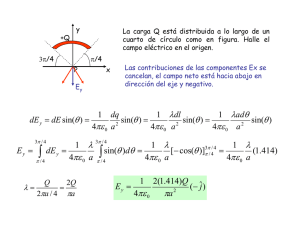
1 Ecuaciones de Maxwell integral y diferencial. Forma integral Forma diferencial 1ª Ley : Flujo eléctrico r r D ∫∫ S ⋅ dS = ∫v ρv dv = r r = QLib ; ∫∫ ε 0 E ⋅dS = QTot S r ∫ ∇ ⋅ D dv = ∫ ρv dv r ρ ∇ ⋅ E = Tot 2ª Ley : Flujo magn. r r B ∫∫ S ⋅ dS = 0 r r Ψ m = ∫∫ B ⋅ dS = S r r = ∫ A ⋅ dl r ∇ ⋅ B = 0 ( general ). r ∇ ⋅ B = 0 (estático). Acotaciones(Fasores) Fasores con subíndice s. v εo r ∇ ⋅ D = ρ Lib r ∇ ⋅ D = 0 (en vacío). Ley de Gauss para campos eléctricos. 1ª Ley de Maxwell. r ∇ ⋅ Ds = ρ s / in r r Ds = ε Es v L 3ª Ley : Ley Faraday r r r ∂B r ∫ L E ⋅ dl = − ∫∫S ∂t ⋅ dS dΨm =− dt r r = ∫∫ ∇ × E ⋅ dS S r r r r r ∫ E ⋅ dl = ∫ (u × B) ⋅ dl L L 4ª Ley : Ley Ampère r r H ∫ L ⋅ dl = Iin r r r ∂D = ∫∫ ( J c + ) ⋅ dS S ∂t r r = ∫∫ ∇ × H ⋅ dS S ∂D ∂Φ e = ∂t ∂t Ley de conservación del flujo magnético o de Gauss para campos magnéticos. 2ª Ley de Maxwell. r ∇ ⋅ Bs = 0 r r ∂B Vacío ∇ × E = − ( o no ) ∂t r ∇ × E = 0 (estático) r r ∂B ∇×E = − + ∂t r r Con flujo +∇ × (u × B) estático + mov. cinético r r r ∂D r JD = ; Jc = σ E ∂t r r r ∂D ∇ × H = Jc + ∂t r r ∇ × H = J c (estático) r r r ∂E ∇ × B = µo J + µoε o ∂t r r r J ∂E c 2∇ × B = + ε o ∂t Ley de Faraday o de la inducción. 3ª Ley de Maxwell. r r ∇ × Es = − jω Bs r r Ds = ε Es r r ∇ ⋅ J D = −∇ ⋅ J C = ∂ρv ∂t Ley de Ampère + corriente de desplazamiento = 4ª Ley de Maxwell. r r r ∇ × H s = J cs + jω Ds r r Bs = µ H s 2 Conserv. c arg a / corr. r r dQ ⋅ J dS ∫∫S T = − dt d = − ∫ ρ v dv dt v r r d − ∫∫ D ⋅ dS = dt S r dρ ∇ ⋅ JT = − v dt r I D = ∫∫ J D S r r r JT = J c + J D r ∇ ⋅ ( JT ) = r = ∇⋅∇× H = 0 = ∫ ∇ ⋅ J dv v Ecuaciones de Laplace y Poisson. Fuerza de Lorentz : Cond . de Lorentz 1: r ∇ ⋅ E = 0(estáti cos) Cond . de Lorentz 2 : r ∂V ∇ ⋅ E = − µε ∂t (campos var iables ) Potenciales Escal. ρ dv Q V= =∫ v 4πε R v 4πε R ρl ( r ') dl ' 1 Vr = r r 4πε ∫L r − r ' Vr = Vr = 1 4πε 1 4πε ∫∫S ρ S ( r ') dS ' r r r −r' ρ R dv ∫v v (t − ) u r r r −r' ∇ 2V = 0 ρ ∇ 2V = − v ε r r 2 ∇ A = − µ0 J r r r r F = q( E + u × B) r r F = qE = r ∂A = q( −∇V − ) ∂t r r r dF = Idl × B Potenciales Vector. r r µ Jdv A=∫ v 4π R r J R dv (t − ) r µ u A= r r ∫ v 4π r −r' Ecuaciones de continuidad de la corriente o de la conservación de la carga. r ∇ ⋅ J TS = − jωρ vs r r J Ds = jωε Es r r r J Cs σ J Cs = σ Es ; r = J Ds ωε Re laciones σ , ε , µ r r r r D = ε E = εoE + P r r r r B = µ H = µo ( H + M ) r r r J T = σ E + ρv u r r ∂A E = −∇V − ∂t r r ∂B ∇× E = − ∂t r r ∂ ∇ × E = − (∇ × A) ∂t Ecs. de las ondas de D ' Alembert. r 2 r r ∂ A ∇2 A − 2 = −µ J ∂t ρ ∂ 2V 2 ∇ V − 2 =− v r r ∂t r ε r E y B son : B = ∇ × A r r ∂A E = −∇V − ∂t De los potenciales retardados 3 Differential form Name "Microscopic" equations "Macroscopic" equations Gauss's law Gauss's law for magnetism Maxwell–Faraday equation (Faraday's law of induction) Ampère's circuital law (with Maxwell's correction) "Microscopic" equations Gauss's law Gauss's law for magnetism Maxwell– Faraday equation (Faraday's law of induction) Ampère's circuital law (with Maxwell's correction) "Macroscopic" equations 4 • Potential formulation approach: In advanced classical mechanics it is often useful, and in quantum mechanics frequently essential, to express Maxwell's equations in a potential formulation involving the electric potential (also called scalar potential) φ, and the magnetic potential A, (also called vector potential). These are defined such that: (A) The law of total currents (B) The equation of magnetic force (C) Ampère's circuital law (D) Electromotive force created by convection, induction, and by static electricity. (This is in effect the Lorentz force) (E) The electric elasticity equation (F) Ohm's law (G) Gauss's law (H) Equation of continuity or Potencial escalar y potencial vector Artículo principal: Potencial vector magnético. Como consecuencia matemática de las ecuaciones de Maxwell y además con el objetivo de simplificar sus cálculos se han introducido los conceptos de potencial vector ( ) y potencial escalar ( ). Este potencial vector no es único y no tiene significado físico claro pero se sabe que un elemento infinitesimal de corriente da lugar a una contribución paralela a la corriente.13 Este potencial se obtiene como consecuencia de la ley de Gauss para el flujo magnético, ya que se conoce que si la divergencia de un vector es cero, ese vector como consecuencia define a un rotacional, así:14 5 A partir de este potencial vector y de la ley de Faraday puede definirse un potencial escalar así:12 donde el signo menos ( ) es por convención. Estos potenciales son importantes porque poseen una simetría gauge que nos da cierta libertad a la hora de escogerlos.12 El campo eléctrico en función de los potenciales: Hallamos que con la introducción de estas cantidades las ecuaciones de Maxwell quedan reducidas solo a dos, puesto que, la ley de Gauss para el campo magnético y la ley de Faraday quedan satisfechas por definición. Así la ley de Gauss para el campo eléctrico escrita en términos de los potenciales: y la ley de ampère generalizada Nótese que se ha pasado de un conjunto de cuatro ecuaciones diferenciales parciales de primer orden a solo dos ecuaciones diferenciales parciales pero de segundo orden. Sin embargo, estas ecuaciones se pueden simplificar con ayuda de una adecuada elección del gauge. 6 Principio de conservación de la carga Artículo principal: Carga. Las ecuaciones de Maxwell llevan implícitas el principio de conservación de la carga. El principio afirma que la carga eléctrica no se crea ni se destruye, ni global ni localmente, sino que únicamente se transfiere; y que si en una superficie cerrada está disminuyendo la carga contenida en su interior, debe haber un flujo de corriente neto hacia el exterior del sistema. Es decir la densidad de carga y la densidad de corriente satisfacen una ecuación de continuidad. A partir de la forma diferencial de la ley de Ampère se tiene: que al reemplazar la ley de Gauss y tomar en cuenta que cualquier vector ), se obtiene: o bien en forma integral: (para 7 1 Fórmulas útiles en Electromagnetismo. Ley de Coulomb r QQ ' r r F = k r r 3 ⋅ (r − r ') r −r ' 1 Con k = 4πε o Ley de Coulomb para cargas múltiple: r QQ ' r r FQ = k ∑ r ri 3 ⋅ (r − ri ') i r − ri ' Campo Eléctrico y Potencial Eléctrico en un punto r P ( r ). 1) Distribución de carga volumétrica: r r r ρ( rr ') (r − r ') 1 1 E= dv ' ; V = r r ∫ 3 4πε o v ' r − r ' 4πε o ρ( rr ') ∫v ' rr − rr ' dv ' 2) Distribución de carga superficial: r E= r 1 4πε o ∫S ' r σ ( rr ') ( r − r ') r r 3 r −r' dS ' ; V = σ ( rr ') 1 4πε o 3) Distribución de carga lineal: r r r λ( rr ') (r − r ') 1 1 E= dl ' ; V = r r ∫ 3 4πε o L ' r − r ' 4πε o ∫S ' rr − rr ' dS ' λ( rr ') ∫L ' rr − rr ' dl ' Teorema de Gauss o de la divergencia: ∫∫ r r r r A ⋅ dS = ∫∫ A ⋅ nˆ dS = ∫∫∫ ∇ ⋅ Adv Ley de Gauss para el campo eléctrico. Forma integral: ∫∫ S ' r 1 E ⋅ dS ' = 1 ρ r dv ' ∑q = ε o i i ε o ∫v ' ( r ') r ρ( rr ') Forma diferencial: ∇ ⋅ E = εo También puede expresarse de la forma: 8 r d Ψe D= eˆn dS r r Ψ e = Qcontenida = ∫∫ d Ψ e = ∫∫ D ⋅ dS S S r r r r Por el teorema de Gauss: ∫∫ D ⋅ dS = ∫ ∇ ⋅ D dv ∴→ ∇ ⋅ D = ρ v S v Teorema de Stokes o del Rotor. ∫L r r r r A ⋅ dl = ∫∫ (∇ × A) ⋅ dS S Teoremas de Green. En base al teorema de Gauss o de la divergencia, si al vector igual a: r A = U .∇V segunda, se tendrá: con U ∫∫ S r A lo hacemos y V funciones escalares con derivadas primera y r r A ⋅ dS = ∫∫ S r (U ∇V ) ⋅ dS = ∫ ∇ ⋅ (U ∇V ) dv v Utilizando la relación vectorial: ∇ ⋅ (U ∇V ) = ∇U ⋅∇V + U ∇ 2V Se obtiene la primera ecuación de Green: ∫∫ S Si se intercambia U Green: r (U ∇V ) ⋅ dS = ∫ (∇U ⋅ ∇V + U ∇ 2V ) dv v con V y se restan ambas expresiones se tiene la 2ª ecuación de ∫∫ S r (U ∇V − V ∇U ) ⋅ dS = ∫ (U ∇ 2V − V ∇ 2U ) dv v Campo y Potencial Eléctrico de un Dipolo Eléctrico en un punto P muy alejado. Supuesto el dipolo en el origen de coordenadas. 9 r V (r ) = r r p⋅r 1 p.cos θ = 3 4πε o r 4πε o r 2 1 ∂V 1 p.cos θ = ∂r 2πε o r 3 1 ∂V 1 p.sin θ Eθ = − = r ∂θ 4πε o r 2 Er = − r r Con p = q.d momento dipolar eléctrico. Campo eléctrico y potencial debido a cargas distribuidas en el origen. Distribución Homogénea de Cargas tipo: Lineal (Hilo Indefinido) con la carga localizada en el origen. Superficial (Sup. Infinita) con la carga localizada en el origen. Volumétrica (Volumen ‘v’) con la carga localizada en el origen. Campo Eléctrico r E=∫ λL dl eˆ L 4πε R 2 R o r σ S dS E=∫ eˆ S 4πε R 2 R o r ρ v dv E=∫ eˆ v 4πε R 2 R o Potencial V( r ) V( r ) V( r ) λL ( rr ) dl =∫ L 4πε r o σ dS =∫ S S 4πε r o ρ dv =∫ v v 4πε r o El potencial siempre es la diferencia de potencial entre el punto considerado V( r ) y una referencia de potencial nulo, en este caso un punto en el infinito. 10 2 Fórmulas útiles en Electromagnetismo. Ecuaciones de Maxwell para las cargas eléctricas y las corrientes eléctricas estacionarias: r r r E ⋅ dl = 0 ; ∇ × E =0 ∫c r r r D ⋅ dS = Q ; ∇ ⋅ D = ρv int ∫∫ Campo eléctrico conservativo. Ley de Gauss. S Que se resumen en las Ecuaciones de Laplace y de Poisson: ∇ 2V = 0 Para todos los puntos sin cargas eléctricas. ∇ 2V = ρv Para puntos con cargas. ε Dieléctricos (lineales, isotrópicos y homogéneos) y Polarización. r r QvL = − ∫ ∇ ⋅ P dv ; ρ vL = −∇ ⋅ P v r r QSL = ∫∫ P ⋅ dS = S Carga latente sobre la sup. del dieléctrico: r = ∫∫ ρ SL dS ; ρ SL = P ⋅ nˆ Carga latente volumétrica en un dieléctrico: S La densidad del flujo eléctrico de un dieléctrico polarizado equivale a: r r r r r D = ε o E + P ; P = χ eε o E r r r r P = ε r ε o E − ε o E = (ε r − 1)ε o E ∴ ε r = 1 + χ e ; χ e : suceptibilidad dieléctrica. Resistencia y Capacidad: r r E ⋅ dl V ∫ c R= = r r I ∫∫ σ E ⋅ dS S RC = r C= Q V = ∫∫S r r ∫c E ⋅ dl r ε E ⋅ dS ε σ 11 3 Fórmulas útiles en Electromagnetismo. Ecuaciones de Maxwell para campos electromagnéticos estacionarios y corrientes eléctricas constantes: ∫∫ S ∫c v r r E ⋅ dl = 0 ∫∫ S ∫L r r r D ⋅ dS = ∫ ρ v dv =Qint ; ∇ ⋅ D = ρ v r r B ⋅ dS = 0 Ley de Gauss. r ∇× E = 0 Conservación del campo r ∇⋅B = 0 Inexistencia de monopolos. r E. r r r r r r H ⋅ dl = ∫∫ J ⋅ dS = I in ; ∇ × H = J Ley de Ampère. S Potencial magnético escalar: r r r r Si J = 0 → H = −∇Vm dado que J = ∇ × H = ∇ × (−∇Vm ). Potencial magnético vectorial: r r r De ∇ ⋅ B → B = ∇ × A Laplaciano del potencial magnético vectorial: r r ∇ 2 A = − µo J Potencial Vect. de un hilo de corriente estacionaria: Potencial Vect. de una lámina de corriente estacionaria: Potencial Vect. de un volumen de corriente estacionaria: Ley de Biot-Savart: Ley de Lorentz: Fuerza sobre un elemento de corriente. r A= r µ I dl ∫ L 4π R r r µ K dS A= ∫ S 4π R r r µ J dv A= ∫ v 4π R r r r r I dl × R I dl × rˆ dH = = 4π R 3 4π R 2 r r r dF = I dl × B r r r r r du Fuerza sobre una carga en movimiento: F = q ( E + u × B ) = m dt r r r r r r Torque o cupla sobre una espira de corriente: T = r × F = m × B = I S eˆn × B r Momento magnético dipolar: m = I S eˆn 12 r r ∑ mk M = lim ∆v→0 ∆v r r A M = χ m H ( ) ( χ m Susceptibilidad) m r r La magnetización es el momento dipolar por unidad de volumen dm = M dv ' y Magnetización: corresponden a materiales día o paramagnéticos lineales. Materiales diamagnéticos y paramagnéticos lineales: r r r r r B = µ H = µo (1 + χ m ) H = µo ( H + M ) r r µo M × eˆr r Potencial magnético vectorial debido a un dm : dA = dv 2 4 π R r r r µo ∇ × M µo M × eˆn cuya integral conduce a: A= dv + dS S 4π ∫v r R 4π ∫∫ R r r µo J m dv µo K m dS o sea: A= + 4π ∫v R 4π ∫∫ S R r r 2 De lo cual se deduce: J m = ∇ × M ( Am ) densidad de corriente volumétrica latente y o de magnetización. r r K m = M × eˆn ( Am) densidad de corriente superficial latente o de magnetización. r r r r r Además: M = χ m H ; J m = χ m ∇ × H = χ m J Ley de Ampère. r En el vacío: M = 0. Condiciones de frontera: r r r r r B1n = B2 n ; ( H1 − H 2 ) × eˆn12 = K r r O si K = 0 → H1t = H 2t Energía magnética: En un inductor: 1 r r B ⋅ H dv (W ) 2 ∫v 1 Wm = L I 2 (W ) 2 Wm = 13 4 Fórmulas útiles en Electromagnetismo. Ecuaciones de Maxwell para campos armónicos en el tiempo. r Forma Diferencial ∇ ⋅ DS = ρvS r ∇ ⋅ BS = 0 r r ∇ × ES = − jω BS r r r ∇ × H S = J S + jω DS Forma Integral r r D ⋅ dS ∫∫ S r S r = ∫∫∫v ρvS dvr = QrSin ∫∫ S BS ⋅ dS = 0 ; ∫∫S BS ⋅ dS = Ψ mS r r r r d Ψ mS E ⋅ dl = − j ω B ⋅ dS = − S S ∫L ∫∫S r r dt r r r ∫ H S ⋅ dl = ∫∫ ( J S + jω DS ) ⋅ dS = I Sin L S Diferentes formas de la Ley de Faraday. r dΨm ∂B r r r r Ve = − ; Ve = − ∫∫ ⋅ dS ; Ve = ∫ (u × B ) ⋅ dl S ∂t L dt Potenciales variables en el tiempo. r r µ J dv ; A=∫ v 4πε R r r r r r r ∂A ∂ Dado que: B = ∇ × A ; ∇ × E = − (∇ × A ) ∴ ∇ × ( E + ) = 0 ∂t ∂t r r r ∂A r ∂A Cuya solución es: E+ = −∇V ∴ E = −∇V − ∂t ∂t ρ dv V =∫ v v 4πε R Puede deducirse: r r r ρ ρ ∂ ∂ ∇ ⋅ E = v = −∇ 2V − (∇ ⋅ A) ∴ ∇ 2V + (∇ ⋅ A) = − v ∂t ∂t ε ε Y con la condición de Lorentz se obtienen las ecuaciones de onda de D’Alembert para los potenciales y para los campos: r r r ρv ∂ 2V ∂2 E ∂E 2 ∇ V − µε 2 = − o en la forma ∇ E − µε 2 = µσ ε ∂t ∂t ∂t r r r 2 2 r r r ∂ A ∂ H ∂ H ∇ 2 A − µε 2 = − µ J o en la forma ∇ 2 H − µε 2 = µσ ∂t ∂t ∂t 2 Y las ecuaciones de Helmholtz para campos armónicos. 14 r r ∇ 2 E + (ω 2 µε − j µσ ) E = 0 r r ∇ 2 H + (ω 2 µε − j µσ ) H = 0 r r r r 2 2 2 2 2 o de la forma: ∇ E = γ E ; ∇ H = γ H con γ = jωµ (σ + jωε ) 5 Fórmulas útiles en Electromagnetismo. Ecuaciones generales de las ondas electromagnéticas: r r 2r ∂2 E ∂E ∇ E − µε 2 = µσ ∂t ∂t r r 2 r ∂ H ∂ H ∇ 2 H − µε = µσ ∂t ∂t 2 Ecuaciones diferenciales de D’Alembert. Ecuaciones generales de las ondas electromagnéticas para campos armónicos: r r ∇ 2 E + (ω 2 µε − j µωσ ) E = 0 Ecuaciones diferenciales de Helmholtz. r 2r 2 ∇ H + ( − j ) H = 0 ω µε µωσ O en la forma abreviada: r r r r ∇ 2 E = γ 2 E ; ∇ 2 H = γ 2 H con γ 2 = (ω 2 µε − j µωσ ) Ecuaciones generales de las ondas planas electromagnéticas para campos armónicos en el vacío: r r r 2 2 r d E ∂2 E ∂ E ω2 2 2 2 S −u =0→ + β ES = 0 con β = 2 ∂t 2 r ∂z 2 dz 2 u El campo eléctrico ES significa la componente espacial del campo llamada fasor r r r j (ωt − β z ) que no contiene el término temporal: E = Eo e eˆx ; E = ES e jωt Expresiones de los campos eléctricos y magnéticos: r E = Eo e j (ωt −β z ) eˆx r Expresiones complejas. E j (ωt −β z −θη ) H = H o e j (ωt −β z ) eˆ y = o e eˆ y η r j (ω t − β z ) E = Re( Eo e eˆx ) = Eo cos (ωt − β z )eˆx r Expresiones reales. E j (ωt −β z −θη ) E H = Re( o e eˆ y ) = o cos (ωt − β z )eˆ y η η 15 Parámetros de las ondas en el vacío: En un cierto estado de la onda con to ∴ z= ω (t − t o ) β y z : ωt − β z = Cte = ωto que representa la velocidad de un punto a lo largo de z. u equivale a la de la luz: ω 1 u= =c= ∴ β = ω ε o µo Para el vacío, la velocidad β Otras relaciones para el vacío: ε o µo λβ = 2π ; λo = uT = r E ωµ µo E ηo = r = o = o = = 120π (Ω) β εo H Ho ωT 2π = ( m) β β Impedancia intrínseca del vacío. ω t − β z : fase en radianes. ω : frecuencia angular = 2π f = 2π T ;T β : constante de fase o número de onda, en ( Período de la onda. rad 1 ) = ( ) También se llama k . s s 10−9 F εo = = 8,85.10−12 ( ) Permitividad del vacío. 36π m Hy µo = 4π .10−7 ( ) Permeabilidad del vacío. m µo 1 m = c = 3.108 ( ) ; = ηo = 120π (Ω) εo s ε o µo Parámetros de un medio dieléctrico perfecto o sin pérdidas: µ = µ o ; ε = ε r ε o ; β = ω µoε = ω c 1 m εr ( ) µo η o = (Ω ) ε εr ω 1 c m = = ( ) Velocidad de propagación de la onda: u = β µ oε εr s Conductividad: σ = 0 λ 2π 2π 2π c Longitud de onda: λ = = = = o ( m) β ω µoε ω ε r εr Angulo de pérdidas: θη = 0( rad ) Impedancia del medio: η = Zm = 16 Parámetros de un medio que es un buen conductor: σ ∞σ S ω 2π 107 ( ) ; ε = ε o ; µ = µ r µo ; u = ; λ= ; m β β Constante de atenuación y de fase: α γ = α + j β = ωµσ ∠ π =β = ωµσ 2 1 = π f µσ ( ) m Cte. de propagación. 4 π ωµ π ωµ j 4 η= ∠ = e = σ 4 σ Impedancia del medio: ωµ π π ωµ = (cos + j sin ) = (1 + j ) (Ω) σ 4 4 2σ σ Tangente de pérdidas: ξ = tan 2θη = ωε Penetración pelicular: δ= 1 α = Resistencia superficial o pelicular: 2 ωµσ ( m) ∴ η = RS = Re [η ] = 1 σδ 1 σδ (1 + j ) (Ω ) Parámetros de un medio dieléctrico de altas pérdidas: µ = µr µo ; ε = ε r ε o ; σ : puede adquirir cualquier valor. µε σ Coeficiente de atenuación: α = ω ( 1 + ξ 2 − 1) con ξ = tan(2θη ) = 2 ωε µε σ Constante de fase: β = ω ( 1 + ξ 2 + 1) con ξ = tan(2θη ) = 2 ωε Constante de propagación: 1 m γ = α + jβ ( ) µ jωµ ε ( Ω) η = Impedancia intrínseca del medio: η = 1 σ + jωε 1 + ξ 2 4 Tangente de pérdidas: ξ = tan 2θη = σ ωε α 1 + ξ 2 −1 1 Penetración pelicular: δ = ( m) Relación: = α β 1 + ξ 2 + 1 1 2 17 Parámetros de la reflexión: Coeficiente de reflexión: ΓE = Ero η 2 − η1 H η −η = ; Γ H = ro = 1 2 = −Γ E Eio η 2 + η1 H io η2 + η1 Coeficiente de transmisión: τE = Eto H 2η 2 2η1 η ; τ H = to = = =τE 1 Eio η 2 + η1 H io η 2 + η1 η2 1+ Γ = τ ; s = 1+ Γ 1− Γ Razón de onda estacionaria. Si σ 1 = 0 y σ 2 = ∞ µ ∴ η1 = ∠0º ; Γ E = −1 ; τ = 0. = = 0 y α α ε 1 2 Si σ 1 = σ 2 = 0 y α1 = α 2 = 0 y η2 >η1 ∴ Γ E > 0 . Potencia y Energía. El vector de Poynting está relacionado con la rapidez con que fluye la energía y representa la cantidad de energía que fluye en la unidad de tiempo (potencia) a través de un área unitaria ubicada perpendicularmente a su dirección de propagación. r r r P = E × H Si los campos son reales. Vector Poynting: r r r P = E × H Para campos complejos en general. Explícitamente es: r r r Eo2 −2α z W P( z ;t ) = E × H = e cos (ωt − β z ).cos (ωt − β z − θη ) eˆz ( 2 ) η m Este valor es instantáneo para cada punto del espacio por lo cual tiene poco valor práctico. Sirve para hallar su valor medio temporal o potencia promedio temporal irradiada. T r r r* Eo2 −2α z 1 r 1 W Pm = ∫ P( z ; t ) dt = Re( E × H ) = e cos θη eˆz ( 2 ) T0 2 2η m Si el medio no tiene pérdidas, el vector de Poynting es: T r r r* Eo2 1 r 1 W Pm = ∫ P( z ; t ) dt = Re( E × H ) = eˆz ( 2 ) T0 2 2η m La potencia promedio temporal que atraviesa una superficie es: r r PPT = ∫∫ Pm ⋅ nˆ dS (W ) ; Si Pm y dS son constantes PPT = P.S .cos ϕ S
Anuncio
Documentos relacionados
Descargar
Anuncio
Añadir este documento a la recogida (s)
Puede agregar este documento a su colección de estudio (s)
Iniciar sesión Disponible sólo para usuarios autorizadosAñadir a este documento guardado
Puede agregar este documento a su lista guardada
Iniciar sesión Disponible sólo para usuarios autorizados