Cálculo integral de funciones de varias variables

Fundamentos Matemáticos de la Ingenierı́a. (Tema 9) Hoja
1
Escuela Técnica Superior de Ingenierı́a Civil e Industrial (Esp. en Hidrologı́a)
Fundamentos Matemáticos de la Ingenierı́a.
Tema 9: Cálculo integral de funciones de varias variables
1
Curso 2008-09
Integrales dobles
1.1
Integrales iteradas y área en el plano
1.1.1
Integrales iteradas
En el tema anterior se mostró cómo calcular la derivada parcial de una función de varias variables, derivando
respecto a cada una de las variables considerando las demás como constantes. Pues bien, utilizando un proceso
similar podemos integrar funciones de varias variables. Por ejemplo si partimos de la derivada parcial fx (x, y) =
2xy, podemos integrar respecto a x, considerando y constante, para obtener la función de partida f (x, y). Esto
es
Z
Z
Z
f (x, y) = fx (x, y) dx = 2xy dx = y 2x dx = yx2 + C(y)
La constante de integración pasa a ser una función de y, ya que cualquier expresión que sólo dependa de y,
darı́a cero al ser derivada respecto a x.
En cuanto a las integrales definidas, se puede aplicar el teorema fundamental del cálculo (considerando a y
como constante).
Z 2y
£
¤2y
2xy dx = yx2 1 = y(2y)2 − y(1)2 = 4y 3 − y
1
De forma análoga se puede integrar respecto a y, considerando x como constante. Ambos procedimientos se
expresan como sigue
Z
h2 (y)
h1 (y)
Z
h (y)
fx (x, y) dx = [f (x, y)]h21 (y) = f (h2 (y), y) − f (h1 (y), y)
g2 (x)
g1 (x)
g (x)
fy (x, y) dy = [f (x, y)]g21 (x) = f (x, g2 (x)) − f (x, g1 (x))
Ejemplos:
Z
x
• Evaluar
(2x2 y −2 + 2y) dy.
1
Z
x
Z
(2x2 y −2 + 2y) dy = 2x2
1
x
Z
1
Z
2
·Z
x
• Evaluar
1
Z
1
2
x
y −2 dy+
1
·
¸x µ
¶ µ
¶
2x2
2x2
2x2
2y dy = −
+ y2 = −
+ x2 − −
+ 1 = 3x2 −2x−1
y
x
1
1
¸
(2x2 y −2 + 2y) dy
dx.
1
·Z
x
1
¸
(2x2 y −2 + 2y) dy
Z
dx =
1
2
£
¤2
(3x2 − 2x − 1) dx = x3 − x2 − x 1 = 2 − (−1) = 3
Fundamentos Matemáticos de la Ingenierı́a. (Tema 9) Hoja
2
La integral del último ejemplo es una integral iterada. Las integrales iteradas se escriben normalmente
Z b Z g2 (x)
Z d Z h2 (y)
f (x, y) dy dx
y
f (x, y) dx dy
a
g1 (x)
c
h1 (y)
Los lı́mites interiores de integración pueden ser funciones de la variable externa, pero los lı́mites exteriores de
integración deben ser constantes. Los lı́mites de integración de una integral iterada determinan la región de
integración R. En nuestro ejemplo R = {(x, y) / 1 ≤ x ≤ 2 ; 1 ≤ y ≤ x}.
Las propiedades de las integrales definidas pueden aplicarse en el cálculo de integrales iteradas.
1.1.2
Área de una región plana
Consideremos la región plana R acotada por a ≤ x ≤ b y g1 (x) ≤ y ≤ g2 (x). El área de R está dada por la
Z b
Z b Z g2 (x)
integral definida
[g2 (x) − g1 (x)] dx, la cual puede ser reescrita como la integral iterada
dy dx,
a
esto es
a
g1 (x)
1. Si R está definida por a ≤ x ≤ b y g1 (x) ≤ y ≤ g2 (x), donde g1 y g2 son continuas en [a, b], entonces el
área de R está dada por
Z b Z g2 (x)
A=
dy dx
a
g1 (x)
2. Si R está definida por h1 (y) ≤ x ≤ h2 (y) y c ≤ y ≤ d, donde h1 y h2 son continuas en [c, d], entonces el
área de R está dada por
Z d Z h2 (y)
A=
dx dy
c
h1 (y)
Nota: En caso de que los cuatro lı́mites de integración sean constantes, la región R es un rectángulo.
Ejemplos:
• Utilizar una integral iterada para hallar el área de la región limitada por las gráficas de f (x) = sen x y
π
5π
g(x) = cos x, entre x = y x =
.
4
4
Z 5π
Z sen x
Z 5π
Z 5π
√
4
4
4
5π
sen x
Área =
[y]cos x dx =
(sen x − cos x) dx = [−cos x − sen x] π4 = 2 2
dy dx =
π
4
cos x
π
4
4
π
4
Z
2
Z
4
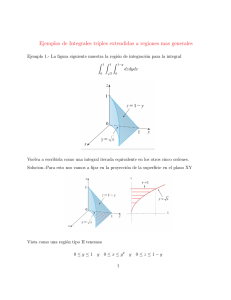
• Describir la región cuya área está representada por la integral
dx dy. Después hallar otra integral
0
y2
iterada que utilice el orden dy dx para representar la misma área y mostrar que ambas integrales dan el
mismo valor.
Los lı́mites de integración nos indican que y 2 ≤ x ≤ 4 y 0 ≤ y ≤ 2, lo que muestra que la región es la que
se encuentra delimitada por el arco de la curva x = y 2 que une los puntos (0, 0) y (4, 2) y el eje OX. El
valor del área es
·
¸2
Z 2
Z 2Z 4
Z 2
y3
16
2
4
(4 − y ) dy = 4y −
dx dy =
[x]y2 dy =
=
u.a.
3
3
2
0
0
y
0
0
Para cambiar el orden de integración a dy dx, hemos de describir la región de forma que x se mueva entre
constantes (integral externa) y la y entre funciones (integral interna). Si tenemos en cuenta que el arco de
curva que delimita nuestra región une los puntos (0, 0) y (4, 2), es obvio que 0 ≤ x ≤ 4. En cuanto a la y,
y dado que por debajo es el eje OX quien acota la región y por arriba lo hace la curva x = y 2 , obtenemos
Fundamentos Matemáticos de la Ingenierı́a. (Tema 9) Hoja
0≤y≤
√
Z
Z
√
x
x. Por lo tanto el área de la región puede hallarse también mediante la integral
Es fácil comprobar que el valor de esta integral coincide con la anterior
·
¸4
Z 4 Z √x
Z 4 √
Z 4
√
2 3
16
x
dy dx =
[y]0 dx =
x dx =
x2 =
u.a.
3
3
0
0
0
0
0
1.2
4
3
dy dx.
0
0
Integrales dobles y volúmenes
Considérese una función continua f tal que f (x, y) ≥ 0 para todo (x, y) en una región R del plano xy. Nos
planteamos calcular el volumen de la región sólida comprendida entre la superficie dada por z = f (x, y) y el
plano xy. Para comenzar subdividimos la región R en rectángulos, quedando algunos rectángulos incompletos
en el borde de R. Los rectángulos (completos) que se encuentran contenidos en R, forman una partición
interior ∆, cuya norma ||∆|| está definida como la longitud de la diagonal más larga de los n rectángulos que
la constituyen. Después se elige un punto (xi , yi ) en cada rectángulo y se construye el prisma rectangular de
altura f (xi , yi ). Si denotamos por ∆Ai al área del rectángulo i-ésimo, el volumen del correspondiente prisma
será f (xi , yi )∆Ai , y el volumen de la región sólida se puede aproximar por la suma de Riemann de los volúmenes
n
X
de los n prismas
f (xi , yi )∆Ai . Esta aproximación se puede mejorar subdividiendo R en rectángulos cada
i=1
vez más pequeños, lo que sugiere que se podrı́a obtener el volumen exacto tomando un lı́mite. Es decir,
Volumen = lim
||∆||→0
n
X
f (xi , yi )∆Ai
i=1
El uso del lı́mite de una suma de Riemann para definir un volumen es un caso particular del uso del lı́mite
para definir una integral doble.
Definición.- Si f está definida en una región cerrada y acotada R del plano xy, entonces la integral doble
de f sobre R está dada por
Z Z
n
X
f (x, y) dA = lim
f (xi , yi )∆Ai
||∆||→0
R
i=1
siempre que el lı́mite exista, en cuyo caso f es integrable sobre R.
Nota: Si f es integrable en una región plana R y f (x, y) ≥ 0 para todo (x, y) ∈ R, entonces el volumen de la
región sólida que se encuentra sobre R y bajo la gráfica de f se define como
Z Z
V =
f (x, y) dA
R
Teorema
Sean f y g continuas en una región cerrada y acotada R del plano, y sea c una constante.
Z Z
Z Z
1.
cf (x, y) dA = c
f (x, y) dA
Z Z
R
2.
R
Z Z
Z Z
[f (x, y) ± g(x, y)] dA =
Z Z
R
f (x, y) dA ±
R
g(x, y) dA
R
f (x, y) dA ≥ 0, si f (x, y) ≥ 0
3.
Z Z
R
4.
Z Z
f (x, y) dA ≥
Z Z
R
5.
g(x, y) dA, si f (x, y) ≥ g(x, y)
Z Z
R
f (x, y) dA =
R
que no se superponen.
Z Z
f (x, y) dA +
R1
f (x, y) dA, donde R es la unión de dos subregiones R1 y R2
R2
Fundamentos Matemáticos de la Ingenierı́a. (Tema 9) Hoja
1.2.1
4
Evaluación de integrales dobles
Normalmente, el procedimiento para evaluar una integral doble pasa por reescribirla como una integral iterada.
El teorema siguiente, conocido como teorema de Fubini, pone de manifiesto esta cuestión.
Teorema
Sea f continua en una región plana R.
1. Si R está definida por a ≤ x ≤ b y g1 (x) ≤ y ≤ g2 (x), donde g1 y g2 son continuas en [a, b], entonces
Z b Z g2 (x)
Z Z
f (x, y) dA =
f (x, y) dy dx
R
a
g1 (x)
2. Si R está definida por c ≤ y ≤ d y h1 (y) ≤ x ≤ h2 (y), donde h1 y h2 son continuas en [c, d], entonces
Z Z
Z d Z h2 (y)
f (x, y) dA =
f (x, y) dx dy
R
Ejemplos:
Z Z µ
• Evaluar
R
1
1
1 − x2 − y 2
2
2
c
h1 (y)
¶
dA, donde la región R viene dada por los puntos que verifican 0 ≤ x ≤ 1,
0 ≤ y ≤ 1.
Por la descripción de R, podemos utilizar cualquier orden de integración.
¶
¶ ¸
Z Z µ
Z 1 ·Z 1 µ
1
1
1
1
2
1 − x2 − y 2 dA =
1 − x2 − y 2 dy dx =
2
2
2
2
3
R
0
0
• Hallar el volumen de la región sólida acotada por el paraboloide z = 4 − x2 − 2y 2 y el plano xy.
Haciendo z = 0, se comprueba que el borde de la región sobre el plano xy es la elipse x2 + 2y 2 = 4, luego
nuestra región de integración la constituyen los puntos sobre la elipse y en el interior de ésta y queda
descrita por
r
r
4 − x2
4 − x2
−2 ≤ x ≤ 2,
−
≤y≤
2
2
Por lo tanto el volumen pedido es
p 2
4−x
Z 2Z
Z
2
V =
p 2 (4 − x2 − 2y 2 ) dy dx =
−2
−
p 2
·
¸ 4−x
Z 2
3
2
3
2y
4
√
(4 − x2 )y −
dx
=
(4 − x2 ) 2 dx =
p 2
4−x
3
3
2
−2
−2
−
2
4−x
2
2
efectuando el cambio de variable x = 2 sen θ
¶2
Z π2
Z π2 µ
√
4
128
1 + cos(2θ)
4
= √
16 cos θ dθ = √
dθ = 4 2π u.v.
2
3 2 − π2
3 2 0
2
• Hallar el volumen de la región sólida R acotada por la superficie f (x, y) = e−x y los planos z = 0, y = 0,
y = x y x = 1.
La base de la región sólida en el plano xy está delimitada por las rectas y = 0, x = 1 e y = x, y puede
describirse de las dos maneras siguientes, asociadas a los dos ordenes de integración posible
–
0 ≤ y ≤ 1, y ≤ x ≤ 1. Esta descripción nos llevarı́a al siguiente cálculo
Z 1Z 1
2
V =
e−x dx dy
0
2
y
el cual no es trivial ya que e−x no posee una función elemental como primitiva.
Fundamentos Matemáticos de la Ingenierı́a. (Tema 9) Hoja
–
0 ≤ x ≤ 1, 0 ≤ y ≤ x. En este caso el volumen serı́a
Z 1Z x
Z 1
Z
x
−x2
−x2
V =
e
dy dx =
e
[y]0 dx =
0
0
0
1
2
xe−x dx =
0
5
e−1
u.v.
2e
• Hallar el volumen de la región sólida R acotada superiormente por el paraboloide z = 1 − x2 − y 2 e
inferiormente por el plano z = 1 − y.
Igualando los valores de z obtenemos la intersección de las dos superficies
1
1
1 − y = 1 − x2 − y 2 ⇔ x2 + y 2 − y = 0 ⇔ x2 + (y − )2 =
2
4
Esta intersección respresenta una curva que se encuentra sobre el cilindro circular recto, cuya proyección
1
1
sobre el plano xy es precisamente la circunferencia x2 + (y − )2 = . El volumen pedido será la diferencia
2
4
1
1
entre el volumen del sólido bajo el paraboloide en la región plana x2 + (y − )2 ≤ , menos el del sólido
2
4
bajo el plano en la misma región. Es decir
Z Z √ 2
Z Z √ 2
Z Z √ 2
1
V =
0
y−y
√
−
1
(1 − x2 − y 2 ) dx dy −
y−y 2
0
y−y
−
√
1
y−y
(1 − y) dx dy =
y−y 2
0
−
√
(y − x2 − y 2 ) dx dy =
y−y 2
√
¸ y−y2
Z 1·
Z
Z
3
3
x
4 1
4 1 1
2
2 32
=
(y − y )x −
(y − y ) dy =
[1 − (2y − 1)2 ] 2 dy
√ 2 dy = 3
3
3
8
0
0
0
− y−y
efectuando el cambio de variable 2y − 1 = sen θ y aplicando dos veces la fórmula cos2 x =
V =
1 + cos(2x)
2
π
u.v.
32
1.2.2
Cambio de variables: coordenadas polares
Z b
En una integral simple
f (x) dx se puede efectuar un cambio de variable x = g(u), con lo que dx = g 0 (u) du,
y obtener
a
Z
Z
b
d
f (x) dx =
a
f [g(u)] g 0 (u) du
c
donde a = g(c) y b = g(d). Nótese que el proceso de cambio de variable introduce en el integrando un factor
adicional, g 0 (u). Esto también ocurre en el caso de integrales dobles
¯
¯
Z Z
Z Z
¯ ∂x ∂y
∂y ∂x ¯¯
¯
f (x, y) dA =
f [g(u, v), h(u, v)] ¯
−
du dv
∂u ∂v
∂u ∂v ¯
R
S
donde el cambio de variables x = g(u, v) e y = h(u, v) introduce un factor llamado jacobiano.
Definición.- Si x = g(u, v) e y = h(u, v), entonces
∂(x, y)
, es
∂(u, v)
¯
¯ ∂x
¯
∂(x, y) ¯¯ ∂u
=¯
∂(u, v) ¯ ∂y
¯
¯
∂u
Ejemplo:
el jacobiano de x e y con respecto de u y v, denotado por
¯
¯
¯
¯ ∂x ∂y
∂y ∂x
¯
−
¯=
¯
∂u
∂v
∂u
∂v
∂y ¯
¯
∂v
∂x
∂v
Fundamentos Matemáticos de la Ingenierı́a. (Tema 9) Hoja
6
• Hallar el jacobiano para el cambio de variables que nos lleva de las coordenadas cartesianas a las polares.
Es decir
x = r cos θ e y = r sen θ
¯
¯
¯ ∂x ∂x ¯ ¯
¯
¯
¯ ¯
cos θ −r sen θ ¯¯
∂(x, y) ¯¯ ∂r ∂θ ¯¯ ¯¯
¯ = r cos2 θ + r sen2 θ = r
=¯
¯=
¯
¯ ∂y ∂y ¯ ¯¯
∂(r, θ)
sen θ r cos θ ¯
¯
¯
¯
¯
∂r ∂θ
Teorema (Cambio de variables)
Sean R y S las regiones en los planos xy y uv que están relacionadas por las ecuaciones x = g(u, v) e
y = h(u, v) de manera que cada punto en R es la imagen de un único punto en S. Si f es continua en R, g y h
∂(x, y)
tienen derivadas parciales continuas en S, y
es distinto de cero en S, entonces
∂(u, v)
¯
¯
Z Z
Z Z
¯ ∂(x, y) ¯
¯ du dv
f (x, y) dx dy =
f [g(u, v), h(u, v)] ¯¯
∂(u, v) ¯
R
S
Ejemplos:
• Cambio de variable para simplificar una región
Sea R la región limitada o acotada por las rectas
x − 2y = 0, x − 2y = −4,
Z Z
evaluar la integral doble
3xy dA.
x + y = 4, x + y = 1
R
Si efectuamos el cambio de variables x − 2y = u y x + y = v, conseguiremos que las rectas oblicuas que
delimitan nuestra región de integración se conviertan en rectas paralelas a los ejes u y v en el plano uv,
u = 0, u = −4, v = 1 y v = 4. Despejando x e y en la igualdades anteriores obtenemos
x=
1
(2u + v)
3
y=
1
(u − v)
3
lo cual implica que el jacobiano es
¯
¯ ∂x
¯
∂(x, y) ¯¯ ∂u
=¯
∂(u, v) ¯ ∂y
¯
¯
∂u
¯
¯ ¯
¯ ¯
¯ ¯
¯ ¯
¯=¯
∂y ¯¯ ¯
¯
∂v
∂x
∂v
2
3
1
3
1
3
− 31
¯
¯
¯
¯ = −1
¯
3
¯
por lo tanto
¯
¸¯
Z Z
Z Z ·
Z 4Z 0
¯ ∂(x, y) ¯
1
1
1
164
¯
¯
3xy dA =
3 (2u + v) (u − v) ¯
(2u2 − uv − v 2 ) du dv =
¯ du dv =
3
3
∂(u,
v)
9
9
R
S
1
−4
• Cambio de variable a coordenadas polares
2
2
2
2
Sea
Z Z R la región anular comprendida entre los cı́rculos x + y = 1 y x + y = 5. Evaluar la integral
(x2 + y)dA.
R
Fundamentos Matemáticos de la Ingenierı́a. (Tema 9) Hoja
7
Efectuando el cambio de√variables x = r cos θ, y = r sen θ, la región R viene descrita como los puntos
(r, θ) tales que 1 ≤ r ≤ 5, 0 ≤ θ ≤ 2π. El correspondiente jacobiano será, como ya hemos visto,
∂(x, y)
=r
∂(r, θ)
Además x2 = r2 cos2 θ e y = r sen θ. Por lo tanto
Z Z
Z
2π
(x2 + y)dA =
R
1.3
√
5
Z
0
(r2 cos2 θ + rsen θ) r dr dθ = 6π
1
Problemas de la sección
1. Evaluar las siguientes integrales iteradas
Z 1Z 2
Z
a)
(x + y) dy dx
b)
0
0
π
Z
(1 + cos x) dy dx
0
1
Z
(x + y) dx dy
0
2
Z √4−y2
0
0
2
3
x
p
1 − x2 dy dx
0
e)
0
sol :
Z
0
sol : 2
Z √1−y2
d)
1
c)
0
sol : 3
Z
Z
sen x
sol :
Z
2
p
dx dy
4 − y2
π
2
f)
0
sol : 4
Z
1
3
sen θ
θ r dr dθ
0
sol :
π2
1
+
32 8
2. Hallar el área de la región R que se encuentra bajo la parábola y = 4x − x2 , sobre el eje OX y sobre la
recta y = −3x + 6.
15
sol:
u.a.
2
3. Idem para la región limitada por las rectas 2x − 3y = 0, x + y = 5, y = 0.
sol: 5 u.a.
4. Determinar la región R cuya área viene dada por la integral iterada. Después cambiar el orden de
integración y mostrar que ambos órdenes dan la misma área.
Z
1
Z
a)
Z
2
dy dx
0
0
0
−
√
Z
dx dy
1−y 2

R: semicı́rculo superior



Z 1 Z √1−x2
sol :

π


dy dx =
2
−1 0
0
Z
2
Z
2
5. Evaluar la integral iterada
integración.
e4 − 1
.
sol:
2e4
Z √1−y2
b)

R: rectángulo



Z 2Z 1
sol :



dx dy = 2
0
1
0
x
2
2
Z
c)
Z
x
4
Z
dy dx +
0
0
4−x
dy dx
2
0

R: triángulo isósceles



Z 2 Z 4−y
sol :


dx dy = 4

0
y
e−y dy dx. Nótese que habrá que efectuar un cambio en el orden de
Fundamentos Matemáticos de la Ingenierı́a. (Tema 9) Hoja
8
6. En los siguientes ejercicios dar una integral para cada orden de integración y utilizar el orden más conveniente para evaluar la integral en la región acotada R delimitada por las igualdades indicadas.
 Z Z
y
 Z Z
 Z Z

y
y
dA




2
2
dA
dA



R x +y



2 + y2
2



x
1
+
x
R
R






 2


x + y 2 = 25

a)
b)
c)

y
=
x
y
=
0









√
3x − 4y = 0






R≡



 R ≡  y = 2x
 R≡ y= x

y=0




x=2
x=4

x≥0
µ ¶
5
sol : ln
2
sol :
ln 17
4
sol : 25
7. Dar, en cada caso, una integral doble para hallar el volumen del sólido limitado o acotado por la gráficas
de las ecuaciones que se indican.
1
.
8
32
(b) z = x2 , z = 0, x = 0, x = 2, y = 0, y = 4.
sol:
.
3
16
.
(c) z = x + y, x2 + y 2 = 4, primer octante.
sol:
3
(a) z = xy, z = 0, y = x, x = 1, primer octante.
sol:
8. Evaluar las siguientes integrales iteradas (nótese que es nacesario cambiar el orden de integración).
Z 1 Z 12
Z ln 10 Z 10
Z 1 Z arccos y
p
1
−x2
a)
e
dx dy b)
dy dx
c)
sen x 1 + sen2 x dx dy
y
0
0
ex ln y
0
0
2
1
sol : 1 − e− 4
sol : 9
Z
2
sol :
Z
d)
0
sol :
√
2
x2
2
√
1 √
[2 2 − 1]
3
y cos y dy dx
2[2sen2 + cos2 − 1]
Z Z
9. Utilizar coordenadas polares para escribir y evaluar la integral doble
f (x, y) dA.
R

 f (x, y) = x + y
a)

R : x2 + y 2 ≤ 4, x ≥ 0, y ≥ 0
sol :
16
3

³y´

 f (x, y) = arctag
x
b)


R : x2 + y 2 ≥ 1, x2 + y 2 ≤ 4, 0 ≤ y ≤ x
sol :
3π 2
64
10. Utilizar una integral doble en coordenadas polares para hallar el volumen del sólido limitado o acotado
por las gráficas de las ecuaciones
p
a) z = xy, x2 + y 2 = 1, primer octante b) z = x2 + y 2 , z = 0, x2 + y 2 = 25
sol :
1
8
sol :
250π
3