parabola - UE Colegio Los Pirineos Don Bosco

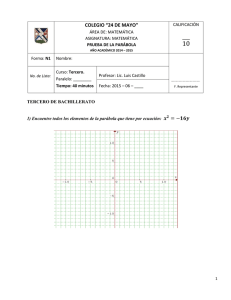
UNIDAD EDUCATIVA COLEGIO
“LOS PIRINEOS DON BOSCO”
INSCRITO EN EL M.P.P.L
N° S2991D2023
RIF: J-09009977-8
GUIA DIDACTICA
MATEMATICA 5to
PARABOLA
Asignatura: Matemática
Año Escolar: 2013-2014
Lapso: 2do
Año: 5to
Secciones: A-B-C
Docente: Lcdo. Molero G. Renso M.
INSTRUCCIONES:
1) La guía de ejercicios se desarrollará en el
cuaderno respectivo a la asignatura.
2) Los ejercicios se deben realizar de la manera
en que se desarrollan en la Guía
NOTA: Esta guía didáctica está basada en el Libro
Texto Matemática II (William Suarez) y Objetivo
Nuevo 3.2 señalado en el Plan de Lapso-
GEOMETRIA EN EL PLANO
PARABOLA:
Es el lugar geométrico de los puntos del plano
que equidistan de un punto fijo “F” llamado
foco y de una recta fija llamada directriz.
Elementos de la parábola:
 D es la directriz
 F es el foco
 Eje focal ó eje de la parábola ó eje de
simetría es la recta perpendicular (eje y) a la
directriz que pasa por el foco y el vértice.
 El vértice V es el punto de intersección de los
ejes con la parábola. Es el punto medio de AF,
punto medio entre el foco y la directriz.
 El parámetro p es la distancia del foco al
vértice
 El lado recto es el segmento perpendicular al
eje de la parábola. El lado recto RS tiene
como longitud cuatro veces la distancia del
vértice al foco.
TIPOS DE PARABOLAS:
FORMULAS:
1) Ecuación Canónica de la Parábola Vertical Positiva
2
𝑥 = 4𝑝𝑦
P  es positivo
Vértice es el origen de coordenadas  V(0,0)
Foco de la Parábola  F(0,p)
Directriz (D) es la recta y = -p
Lado Recto  |4𝑝|
2) Ecuación Canónica de la Parábola Vertical Negativa
𝑥 2 = −4𝑝𝑦
P  es negativo
Vértice es el origen de coordenadas  V(0,0)
Foco de la Parábola  F(0,–p)
Directriz (D)  es la recta y = p
Lado Recto  |4𝑝|
FORMULAS:
3) Ecuación Canónica de la Parábola Horizontal Positiva
𝑦 2 = 4𝑝𝑥
P  es positivo
Vértice es el origen de coordenadas  V(0,0)
Foco de la Parábola  F(p,0)
Directriz (D) es la recta x = -p
Lado Recto  |4𝑝|
4)Ecuación Canónica de la Parábola Horizontal Negativa
𝑦 2 = −4𝑝𝑥
P  es negativo
Vértice es el origen de coordenadas  V(0,0)
Foco de la Parábola  F(–p,0)
Directriz (D)  es la recta x = p
Lado Recto  |4𝑝|
PROCEDIMIENTO PARA GRAFICAR LA PARABOLA:
1. Se realiza el Plano Cartesiano:
Se dibujan los Ejes (x,y), sus longitudes deben ser cuatro veces el valor de “p”, es decir 4p
Se escriben los números en cada Eje, separados por 1 centímetro cada uno.
2. Utilizando las coordenadas del Vértice, se ubica y señala con un punto (•).
3. Utilizando las coordenadas del Foco, se ubica y señala con un punto (•).
4. Utilizando las coordenadas el punto de intersección “A” con la Recta Directriz “D”, se ubica y señala con
un punto (•).
5. Se dibuja la Recta Directriz “D”, paralela al eje que corresponda a la respectiva Ecuación de la Parábola,
señalado en los Tipos de Parábolas.
6. (Opcional). Si se tiene el valor del Lado Recto de la Parábola, se dibuja y ubican los puntos “R” y “S”,
sabiendo que el Foco es el punto medio del Lado Recto. Nota: observar los Tipos de Parábolas.
7. Se dibuja una CURVA que pase por los siguientes puntos: R - V - S:
Dependiendo del Tipo de Parábola (Observar las gráficas de cada tipo de parábola), la CURVA se
dibujará hacia arriba ó hacia abajo ó hacia la derecha ó hacia la izquierda.
GUIA DE EJERCICIOS
PARÁBOLA
NOTA: Esta guía didáctica está basada en el Libro Texto Matemática II (William Suarez) y Objetivo Nuevo 3.2 señalado
en el Plan de Lapso
I.- Parte: Analiza con cuidado cada una de los ejercicios y determina lo requerido en cada ejercicio:
Ejercicio Propuesto.- Dada la ecuación de la parábola y2 = 8x.
Determinar:
a) las coordenadas del foco y el vértice
b) la longitud del lado recto
c) la ecuación de la directriz.
CALCULAR: a) F(x,y): ¿? V(x,y): ¿? b) Lado Recto: ¿? c) Directriz: ¿?
Se escribe la expresión matemática del FOCO y VERTICE para este tipo de
𝐹(𝑝, 0) y 𝑉(0,0)
Parábola
Se escribe la fórmula de la Ecuación Canónica de la Parábola Horizontal
𝑦 2 = 4𝑝𝑥 ↔ 𝑦 2 = 8𝑥
Positiva y la Ecuación del Ejercicio para luego determinar el valor de p
2
2
a)
Se comparan las Ecuaciones para deducir que valor le corresponde a 4p
𝑦 = 𝟒𝒑𝑥 ↔ 𝑦 = 𝟖𝑥
8
→𝒑=𝟐
4
𝑭(𝟐, 𝟎) y 𝑽(𝟎, 𝟎)
4𝑝 = 8 → 𝑝 =
𝐿𝑎𝑑𝑜 𝑅𝑒𝑐𝑡𝑜 = |4𝑝|
b)
𝐿𝑎𝑑𝑜 𝑅𝑒𝑐𝑡𝑜 = |4.2| = |8|
𝑳𝒂𝒅𝒐 𝑹𝒆𝒄𝒕𝒐 = |𝟖| = 𝟖
c)
𝐷: 𝑥 = −𝑝
𝑫: 𝒙 = −𝟐
Se despeja p y se determina su valor
Se identifican las coordenadas del FOCO y el VERTICE
Se escribe la fórmula del Lado Recto de la Parábola
Se sustituye el valor de p en la fórmula y se realiza la operación respectiva
Se resuelve el valor absoluto y se determina el valor del Lado Recto de la
Parábola
Se escribe la expresión matemática de la DIRECTRIZ (D) para este tipo de
Parábola
Se sustituye el valor de p y se determina la Ecuación de la Recta Directriz
Ejercicio 1.- Dada la ecuación de la parábola y2 = 4x.
Determinar:
a) las coordenadas del foco y el vértice
b) la longitud del lado recto
c) la ecuación de la directriz.
Ejercicio Propuesto.- Dada la ecuación de la parábola x2 = 12y.
Determinar:
a) las coordenadas del foco y el vértice
b) la longitud del lado recto
c) la ecuación de la directriz.
CALCULAR: a) F(x,y): ¿? V(x,y): ¿? b) Lado Recto: ¿? c) Directriz: ¿?
Se escribe la expresión matemática del FOCO y VERTICE para este tipo de
𝐹(𝑜, 𝑝) y 𝑉(0,0)
Parábola
Se escribe la fórmula de la Ecuación Canónica de la Parábola Horizontal
2
2
𝑥 = 4𝑝𝑦 ↔ 𝑥 = 12𝑦
Positiva y la Ecuación del Ejercicio para luego determinar el valor de p
a)
Se comparan las Ecuaciones para deducir que valor le corresponde a 4p
𝑥 2 = 𝟒𝒑𝑦 ↔ 𝑥 2 = 𝟏𝟐𝒚
12
→𝒑=𝟑
4
𝑭(𝟎, 𝟑) y 𝑽(𝟎, 𝟎)
4𝑝 = 12 → 𝑝 =
𝐿𝑎𝑑𝑜 𝑅𝑒𝑐𝑡𝑜 = |4𝑝|
b)
𝐿𝑎𝑑𝑜 𝑅𝑒𝑐𝑡𝑜 = |4.3| = |12|
Se despeja p y se determina su valor
Se identifican las coordenadas del FOCO y el VERTICE
Se escribe la fórmula del Lado Recto de la Parábola
Se sustituye el valor de p en la fórmula y se realiza la operación respectiva
Se resuelve el valor absoluto y se determina el valor del Lado Recto de la
𝑳𝒂𝒅𝒐 𝑹𝒆𝒄𝒕𝒐 = |𝟏𝟐| = 𝟏𝟐
Parábola
Se escribe la expresión matemática de la DIRECTRIZ (D) para este tipo de
𝐷: 𝑥 = −𝑝
Parábola
c)
Se sustituye el valor de p y se determina la Ecuación de la Recta Directriz
𝑫: 𝒙 = −𝟑
Ejercicio 2.- Dada la ecuación de la parábola x2 = 16y.
Determinar:
a) las coordenadas del foco y el vértice
b) la longitud del lado recto
c) la ecuación de la directriz.
Ejercicio Propuesto.- Encontrar la ecuación de la parábola cuyo foco está sobre el eje y a una distancia de
3 unidades por debajo del origen y la directriz es paralela al eje x, pasando por el punto A(0, 3). Realiza su
gráfica:
CALCULAR: Determinar la Ecuación de la Parábola
- Foco esta sobre el eje Y.
- Foco esta distanciado 3 unidades por debajo del origen. Se analiza la información del ejercicio con respecto al
FOCO
𝑭(𝟎, −𝟑)
La Parábola abre hacia abajo debido a que el Foco esta
en 𝑭(𝟎, −𝟑)
Por lo tanto le corresponde la Ecuación 𝒙𝟐 = −𝟒𝒑𝒚
- Directriz es paralela al eje X.
- Directriz pasa por el Punto A(0,3).
𝐴(0,3) → 𝐴(0, 𝑝) entonces 𝒑 = 𝟑
𝑥 2 = −4𝑝𝑦 → 𝑥 2 = (−4). 3𝑦 → 𝒙𝟐 = −𝟏𝟐𝒚
Se describe si la Parábola abre hacia abajo ó hacia arriba,
y se determina la respectiva Ecuación Canónica de la
Parábola
Se analiza la información del ejercicio con respecto a la
DIRECTRIZ
Se sustituye el valor de p; y se determina la Ecuación de
la Parábola
Gráfica de la Parábola
Ejercicio 3.- Encontrar la ecuación de la parábola cuyo foco está sobre el eje y a una distancia de 2 unidades por
abajo del origen y la directriz es paralela al eje X, pasando por el punto A(0, 2). Realiza su gráfica:
Ejercicio Propuesto.- Encuentra la ecuación de la parábola cuyo vértice está en el origen, si se sabe que la
directriz es la recta de ecuación x – 5 = 0:
CALCULAR: Determinar la Ecuación de la Parábola
- Vértice es el origen.
𝑽(𝟎, 𝟎)
- Directriz es la recta de ecuación x – 5 = 0  x = 5.
𝑫: 𝒙 = 𝟓 por lo que 𝑫: 𝒙 = 𝒑 entonces 𝒑 = 𝟓
- La Parábola abre hacia la izquierda debido a que la Directriz es
𝑫: 𝒙 = 𝟓, la cual es una recta paralela al lado derecho del eje Y; por lo
tanto le corresponde la expresión matemática 𝑦 2 = −4𝑝𝑥
𝑦 2 = −4𝑝𝑥 → 𝑦 2 = (−4). 5𝑥 → 𝒚𝟐 = −20𝒙
Se analiza la información del ejercicio con
respecto al VERTICE
Se analiza la información del ejercicio con
respecto a la DIRECTRIZ
Se describe si la Parábola abre hacia la
izquierda ó hacia la derecha, y se
determina la respectiva Ecuación
Canónica de la Parábola
Se sustituye el valor de p; y se determina
la Ecuación de la Parábola
Ejercicio 4.- Encuentra la ecuación de la parábola cuyo vértice está en el origen, si se sabe que la directriz es la
recta de ecuación x + 2 = 0: