1º BT Mat I CNS Ejercicios de geometría, Pag 1 Ejercicios de

1º BT M at I CNS
Ejercicios de vectores
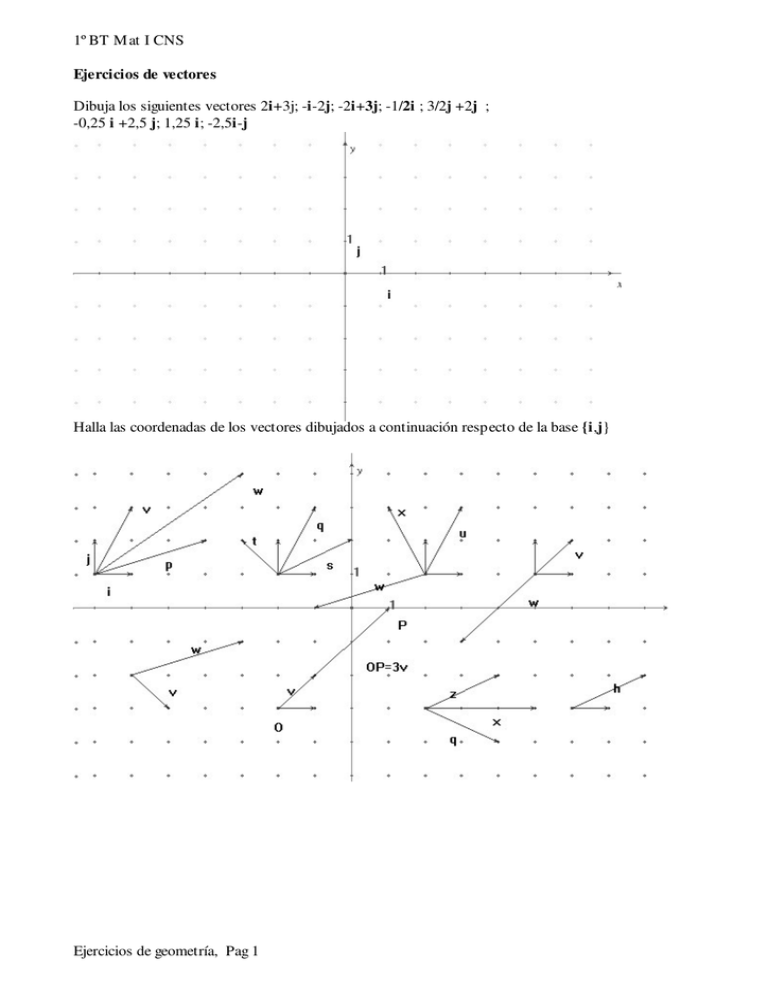
Dibuja los siguientes vectores 2i+3j; -i-2j; -2i+3j; -1/2i ; 3/2j +2j ;
-0,25 i +2,5 j; 1,25 i; -2,5i-j
Halla las coordenadas de los vectores dibujados a continuación respecto de la base {i,j}
Ejercicios de geometría, Pag 1
1º BT M at I CNS
Halla para cada uno de los casos siguientes, las coordenadas del vector x respecto de la base
B={u, v}
Ejercicios de geometría, Pag 2
1º BT M at I CNS
1) Expresa los vectores BC,AC,DG,GC,FD y BD como c. l. de AB y AG
2) Sea HG=u HA=v, expresar IA,DF,AG,ER,HR y BR como c.l. de u y v
3) Expresar AB,MD, CD, CN, MB y AO como c.l. de AD y AM
4) Idem , pon coordenadas a los distintos puntos tomando como base MD y MC
5) Considera un triángulo equilátero, averigua las coordenadas de los vértices.
6) Considera un exágono regular y pon coordenadas a los vértices.
7) Consideramos un hexágono regular de vértices A , B , C , D , E , F y
centro O. Halla las coordenadas en la base {OC, OD } de los siguientes
vectores OA, OB, OE, OF+BA, 3.CD y FA - 2.0A.
Ejercicios de geometría, Pag 3
1º BT M at I CNS
EJERC IC IO S D E GEO METRIA PLAN A
1.-El vector AB=(1,-3); a) hallar las coordenadas de A sabiendo que las coordenadas del punto B
son (0 , 2) ; b) hallar las coordenadas de B sabiendo que las coordenadas del punto A son (-2,3); c)
Si el vector AB=3CD, y las coordenadas de C son (-1,4) halla las coordenadas de D; d) Averiguar
las coordenadas de un vector v sabiendo que v+2AB=BA.
2.-Las coordenadas del punto medio del segmento AB son (3,5). Si B=(0,1) halla las coordenadas
de A.
3.-Halla las coordenadas de los puntos P y Q que dividen al segmento de extremos
A (-5,3) y
B (8,6) en tres partes iguales.
4.-Hallar las ecuaciones paramétricas, continua, general, punto-pendiente y explícita de la recta que
pasa por el punto A(-2,3) y cuyo vector director es v(3,4). a) Halla, si existe, un punto de la recta
que su abscisa sea 6 .b) Halla, si existe, un punto de la recta con ordenada –4.
5.-Halla las diversas formas de la ecuación de la recta:
a) Q ue p as a p or A (3,-1) y B(5,2). b) Q ue p as a p or A (-2,4) y p endient e –2.c)
P as a p or el p unt o A (1,-3) y p aralela a la rect a x+ 3= 0.d) P as a p or el p unt o A (1,2) y es p aralela al eje de abs cis as .
6.- Hallar el valor de k para que:
a) El punto (1,2) pertenezca a la recta x-3ky+3=0;
b) El punto (k,1) pertenezca a la recta x+2y-4=0;
c) Los puntos (1,2) (5,-6) y (7,k) estén alineados.
d) La recta 2x+ky-1= 0 tenga como vector director v=(-5,3).
e) La recta kx-3y+2= tenga de pendiente m=-3/2.
f) Las rectas r: y=9kx+2 y s: 4x-ky+1=0 sean paralelas.
g) Las rectas r: 2x+3ky+2=0 y s:
x −2 y+1
=
se corten en un punto.
−2
k
7.- U na rect a p as a p or el p unt o P (5,6) y cort a a los ejes coordenados s egún
s egment os iguales , ¿ cuál es s u ecuación?.
8. - Un paralelogramo tiene sus vértices A(2,3) y dos de sus lados están sobre las rectas x+y=20 y
2x-3y=10.Calcula las ecuaciones de los otros dos lados y las coordenadas de sus vértices.
9.-Halla la ecuación de la recta que pasa por el punto de corte de r: x-2y+3=0 y s:
x = 1− t
y = −2 + 3t
y por
el punto(-5,0). b) Paralela a y=-1/2x+3 y corta al eje de ordenadas en y=-3.
10.-Halla las ecuaciones explícitas de las rectas de las figuras, a partir de los datos que se indican:
Ejercicios de geometría, Pag 4
1º BT M at I CNS
Vectores y producto escalar.
1.-Escribe el vector(3,8/3) como combinación lineal de los vectores (0,7/3) y (1,4).
2.-Calcula el producto escalar de los vectores dados, el módulo de cada uno y el ángulo que
determinan los vectores que se dan: u= (3,4) y v=(-4,3).b) x=(1,3) e y=(3,-1). c) p=(-1,6) y
q=(3,5).d)u=(2√2,-2) y v=(√2,-1).e)m=(-3,2) y n=(-1/2,-1/3)
3.-Halla el ángulo que forman los vectores AP y AQ en los siguientes casos: a) A(2,0) , P(-2,1) y
Q(6,8) b) A(2,1), P(6,1) y Q(6,1) c) A(0,1) P(2,-2) y Q( 3,0).
4.-Dados los vectores x=(a,1) e y=(2,-3) Calcular a para que: a) el producto escalar de x por y sea
la unidad. b)el módulo de x sea 3. c)el vector x+ay sea unitario. d) x e y sean ortogonales e) tengan
la misma dirección f) formen un ángulo de π/4 radianes. g) formen un ángulo de π/3 radianes.
5.-a)Halla un vector paralelo a v=(1,4), de módulo 3 y del mismo sentido. b) Halla un vector
paralelo a v=(1,4) de módulo 5 y de sentido contrario. c) Halla un vector ortogonal al (-2,3)
unitario. d) Halla un vector ortogonal al (-2,3) de módulo 3.
6.-Los vectores a y b son ortogonales entre sí y forman con el vector c ángulos de π/3 y π/6
radianes respectivamente. Sabiendo que |a|=3, |b|=5 , |c|=8 , calcula a) (3a-2b)(b+3c) b) b.(a+b-c)
c) |(a+b)|.
7.-El triángulo ABC es rectángulo en A, siendo sus vértices los puntos A(3,5) ,B(1,3) y C(m,10)
Halla m.
8.-Sea ABC un triángulo con vértices A(0,0) B(1,3) y C(-2,7). a) Halla el perímetro del triángulo.
b) Halla los ángulos del triángulo. c) Halla las coordenadas del vector AH siendo AH la altura
relativa al lado BC .
9.-Los lados de un paralelogramo están sobre las rectas y=2x, e 3y=x. Si el centro del
paralelogramo es el punto M (1,1), halla las coordenadas de sus vértices.
10.-Hallar la distancia entre las rectas r≡ 3x-4y+3=0 y s≡ y=3x/4+ 4.
11.-Averiguar si el triángulo A(-10,3) ,B(4,8) y C(-7,2) es isósceles .Halla el área y el perímetro de
este triángulo.
12.-Dadas las rectas r≡ 3x+4y-1=0 y s≡ 4x-3y+2=0 hallar: el ángulo que forman. b) ecuaciones de
las bisectrices .
13.- Halla la ecuación de la recta que pasa por A (2,3) y que a) es paralela a r≡3x-y+5=0 b) Es
perpendicular a s≡
x −1
2
=
y +1
−3
c) Es perpendicular a la recta que pasa por P(1,3) y B(-1,3).
14.-Calcula el ángulo que forman los vectores u(2,-3) y v(1,4) así como el ángulo que forman las
rectas r≡
x −1
2
=
y +1
−3
y s≡4x-y-5=0 ¿Qué observas?
15.-Dos vértices de un triángulo son A(1,-2) y B(2,3).Determina el vértice C sabiendo que está
sobre la recta r≡2x+y-2=0 y que el área del triángulo es 8 u2.¿Cuántas soluciones encuentras ?
16.-Halla el punto simétrico de P(10,10) respecto de la recta x+y-10=0.
17.-Determina las coordenadas del punto P(x,y) que equidista de A(1,2) ,B(-6,1) y C(-5,-6).
18.- Halla las ecuaciones de las rectas que pasando por A(1,1) distan dos unidades del punto B(2,3).
19.-Dada la recta r≡x-2y-4=0 y el punto P(1,1) , halla un punto de la recta r que diste 6 del punto P
¿ Cuantas soluciones hay?
5
4
20.-Los lados AB, BC y AC de un triángulo están respectivamente, en las rectas y = x −
;
6
3
x = 2 −t
2x+7y=22 y
Calcula : a) La distancia de cada recta al origen. b) Las coordenadas de
y = 3 + 7t
los vértices A, B y C. c) El valor de las alturas del triángulo. d) Las longitudes de los lados. e)El
área del triángulo. f) La ecuación de la mediana relativa al lado AB. g) la ecuación de la mediatriz
del lado AB. h) ecuación de la bisectriz del ángulo B
Ejercicios de geometría, Pag 5