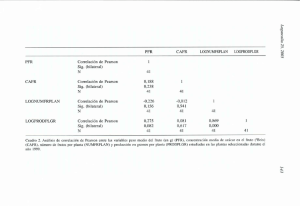
Mo = Li + ·ai fi ai Mo = Li + ·ai x= xi · ni N Me = Li + N

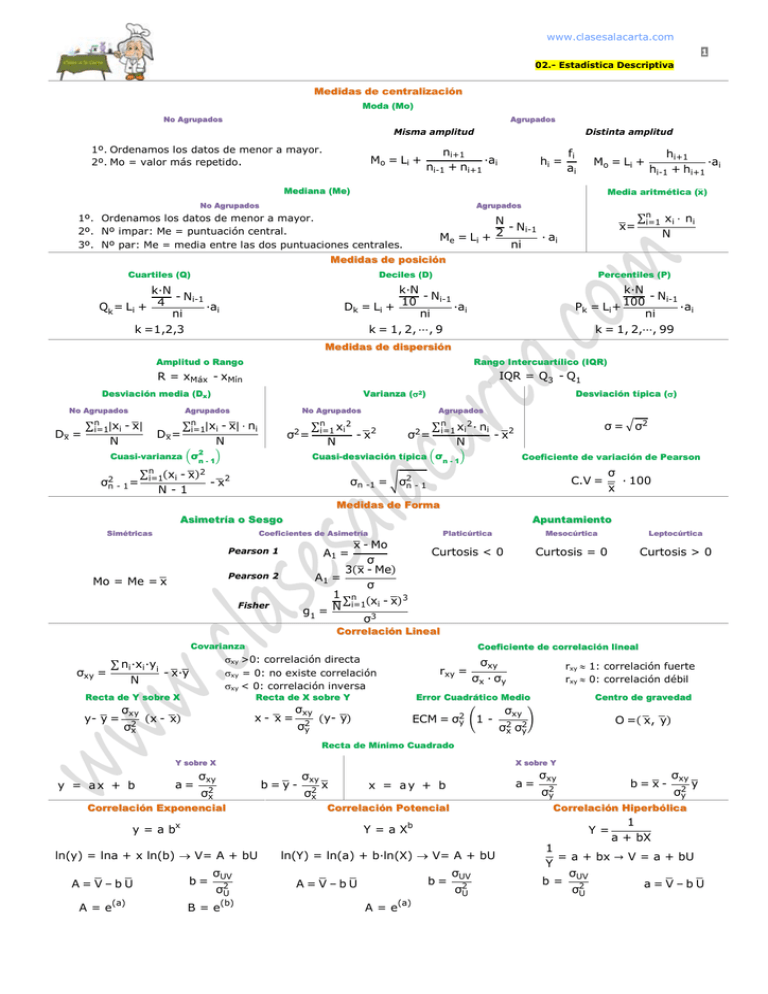
www.clasesalacarta.com
1
02.- Estadística Descriptiva
Medidas de centralización
Moda (Mo)
No Agrupados
Agrupados
Misma amplitud
1º. Ordenamos los datos de menor a mayor.
2º. Mo = valor más repetido.
Mo = Li +
Distinta amplitud
ni+1
·a
ni-1 + ni+1 i
hi =
fi
ai
hi+1
·a
hi-1 + hi+1 i
Mo = Li +
Mediana (Me)
Media aritmética (x)
No Agrupados
Agrupados
1º. Ordenamos los datos de menor a mayor.
2º. Nº impar: Me = puntuación central.
3º. Nº par: Me = media entre las dos puntuaciones centrales.
N
- Ni-1
Me = Li + 2
· ai
ni
x=
n
i=1
xi · ni
N
Medidas de posición
Cuartiles (Q)
Deciles (D)
Percentiles (P)
k·N
- Ni-1
Qk = Li + 4
·ai
ni
k =1,2,3
k·N
- Ni-1
Dk = Li + 10
·ai
ni
k = 1, 2, ⋯, 9
k·N
- Ni-1
Pk = Li + 100
·ai
ni
k = 1, 2,⋯, 99
Medidas de dispersión
Amplitud o Rango
Rango Intercuartílico (IQR)
IQR = Q3 - Q1
R = xMáx - xMín
Desviación media (Dx )
No Agrupados
Dx =
n
i=1
Varianza
Agrupados
xi - x
N
n
i=1
Dx =
xi - x · ni
N
σ2n - 1 =
xi - x
N-1
n
2
i=1 xi
σ2 =
2
2
Desviación típica ()
No Agrupados
Cuasi-varianza σ
n-1
n
i=1
(2)
N
Agrupados
- x2
n
2
i=1 xi · ni
σ2 =
N
Cuasi-desviación típica σn - 1
- x2
σ = σ2
- x2
Coeficiente de variación de Pearson
σn -1 = σ2n - 1
C.V =
σ
· 100
x
Medidas de Forma
Asimetría o Sesgo
Simétricas
Apuntamiento
Coeficientes de Asimetría
x - Mo
A1 =
σ
3 x - Me
A1 =
σ
1 n
i=1 xi - x
g1 = N
σ3
Pearson 1
Pearson 2
Mo = Me = x
Fisher
Platicúrtica
Mesocúrtica
Leptocúrtica
Curtosis < 0
Curtosis = 0
Curtosis > 0
3
Correlación Lineal
Covarianza
ni ·xi ·yi
- x·y
N
σxy =
Recta de Y sobre X
y- y =
σxy
σ2x
Coeficiente de correlación lineal
xy >0: correlación directa
xy = 0: no existe correlación
xy < 0: correlación inversa
rxy =
Recta de X sobre Y
x- x=
x- x
σxy
σ2y
σxy
σx · σy
rxy  1: correlación fuerte
rxy  0: correlación débil
Error Cuadrático Medio
y- y
ECM = σ2y
1-
Centro de gravedad
σxy
O = x, y
σ2x σ2y
Recta de Mínimo Cuadrado
Y sobre X
y = ax + b
a=
X sobre Y
σxy
b=y-
σ2x
Correlación Exponencial
σxy
σ2x
x
a=
x = ay + b
Correlación Potencial
x
b
Y=aX
ln(y) = lna + x ln(b)  V= A + bU
ln(Y) = ln(a) + b·ln(X)  V= A + bU
A=e
(a)
b=
σUV
σ2U
B=e
(b)
Y=
b=
A=V–bU
A=e
(a)
b=x-
σ2y
σxy
σ2y
y
Correlación Hiperbólica
y=ab
A=V–bU
σxy
σUV
σ2U
1
a + bX
1
= a + bx → V = a + bU
Y
σUV
b= 2
a=V–bU
σU