Clase2ModelosenTiempoDiscreto 377KB Mar 14 2016 12:12:08

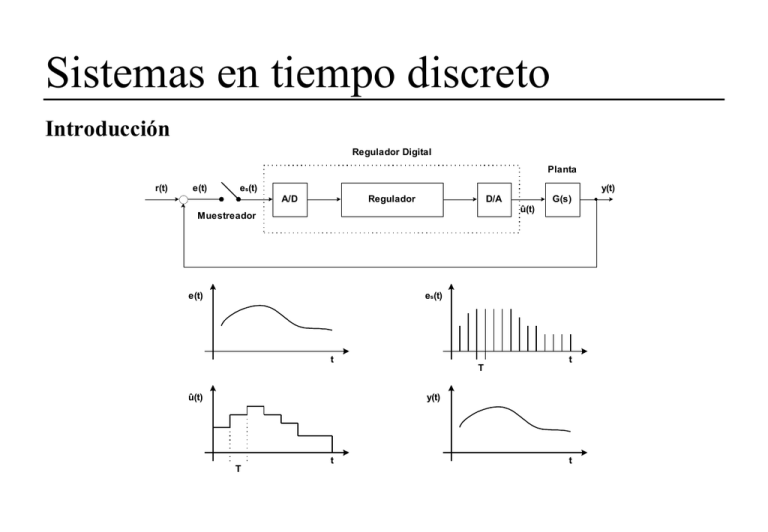
Sistemas en tiempo discreto
Introducción
Regulador Digital
Planta
r(t)
e(t)
es(t)
y(t)
A/D
Regulador
D/A
G(s)
û(t)
Muestreador
e(t)
es(t)
t
û(t)
T
t
y(t)
T
t
t
Características del control en t. discr.
 La planta es continua pero el regulador trabaja en tiempo discreto.
 La estabilidad del sistema en tiempo discreto y la aproximación del
sistema de tiempo continuo a tiempo discreto dependen del periodo de
muestreo T.
Casos típicos de control en tiempo discreto:
 Emulación analógica
 Diseño digital directo
Emulación analógica
Primero se realiza el análisis y la síntesis del regulador en tiempo continuo
y luego se usa un proceso de discretización usando el periodo de muestreo
T.
 La planta se modela en tiempo continuo
 El regulador se diseña en tiempo continuo usando los métodos
conocidos.
 El regulador obtenido del proceso anterior se discretiza usando un
período de muestreo T y empleando alguna de las aproximaciones
conocidas
Aproximaciones para la
discretización de reguladores
 Respuesta invariante (al escalón o al impulso)
 Transformación bilineal o de Tustin
 Mapeo de polos y ceros
 Retenedor de orden cero
Diseño digital directo
La planta en tiempo continuo es discretizada, generalmente por el método
del retenedor de orden cero, obteniéndose así una aproximación digital y
luego se calcula o sintetiza un compensador digital.
 La planta se modela en tiempo continuo
 La planta es discretizada usando el periodo de muestreo T y un
método de aproximación de los antes enumerados.
 El regulador se calcula o sintetiza directamente en tiempo discreto
usando cualquiera de los métodos siguientes:
Métodos de diseño digital directo
 El lugar de las raíces
 Realimentación de estado
 Respuesta de frecuencia o gráficas de Bode (a través de una
transformación bilineal al plano W)
 Respuesta de orden n con cancelación de polos
 Dead-Beat
f(t)
fs(t)
^f(t)
Muestreador
Retenedor
f(t)
fs(t)
t
T
2T 3T 4T 5T 6T
t
^f(t)
T
2T 3T 4T 5T 6T
t
Proceso de la señal de tiempo continuo a tiempo
discreto
f S (t )  f (t )   T (t )

f S (t )  f (t )   (t  kT )
K 0
^
f (t )  f (kT )
; kT  t  (k  1)T
Discretización de sistemas descritos
por ecuaciones diferenciales
Discretización de la ecuación diferencial de primer orden
dy
 ay (t )  bu(t ) ; a, b  cte
dt
Se sustituye en la ecuación anterior t  kT para k = 0, 1, 2 ...
dy
y se despeja dt para obtener:
dy
  ay(t )  bu (t )  t kT
dt t kT
dy
 ay(kT )  bu (kT )
dt t kT
dy
Se aproxima la derivada dt
por el método de Euler para una función
t  KT
y(t) continua.
dy
y ((k  1)T )  y (kT )

dt t  KT
T
La cual es una buena aproximación si el periodo T es pequeño.
y((k  1)T )  y(kT )
 ay(kT )  bu (kT )
T
Se multiplica a ambos lados por T y se simplifica el resultado escribiendo
únicamente k en lugar de kT:
y(kT )  y(k ) y u(kT )  u(k )
y se obtiene:
y(k  1)  aT  y(k )  bT  u(k )  y(k )
Sustituyendo una vez más k 1  k :
y(k )  (1  aT ) y(k 1)  bT  u(k 1)
Ecuación de diferencias correspondiente a la ecuación diferencial de
primer orden.
Comportamiento de un sistema
discreto de primer orden.
Los valores discretos y(k) = y(kT) de la solución de y(t) pueden ser
calculados resolviendo la ecuación de diferencias.
Primero se calcula la solución homogénea: u(k )  0 k por recursión:
y(1)  (1  aT ) y(0)
k 1
k 2
y(2)  (1  aT ) y(1)  (1  aT )(1  aT ) y(0)
k 3
y(2)  (1  aT ) 2 y(0)
y(3)  (1  aT ) y(2)  (1  aT ) 3 y(0)
y(k )  (1  aT ) K y(0) ;
k = 0, 1, 2 ...
Comparación de nuestra aprox. con
la solución continua
y(t )  e  at y(0) ; t  0
Sustituyendo t  kT :
y(kT )  e  akT y(0)
 
k
y(k )  e  aT y(0)
Desarrollando
k = 0, 1, 2 ...
k = 0, 1, 2 ...
e  aT por una serie:
e
aT
aT a 2T 2 a 3T 3
1


 ...
1!
2!
3!
La solución exacta
Sustituyendo obtenemos
K


aT
aT
y (k )  1  aT 

 ... y (0) ;
2!
3!


2
2
3
3
k = 0, 1, 2 ...
Si aT  1 entonces, las potencias de aT serán mucho menores que (1-aT)
y por lo tanto se puede aproximar la solución a:
y(k )  (1  aT ) K y(0)
La cual es una buena aproximación a la solución exacta si aT  1 , y
coincide con la solución encontrada antes.
Satisfacción de las condiciones
1
Para cumplir la condición aT  1 hacemos que T  a con lo que se
puede escoger el periodo de muestreo como:
T
1 1

10 a
Donde a representa el polo de lazo cerrado
Se puede también utilizar la siguiente recomendación:
fs 
1
 20  BW
T
Donde BW es el ancho de banda de lazo cerrado del sistema
La solución completa obtenida por recursión, es:
k

y(k )  (1  aT ) y (0)   1  aT  bT  u (i  1)
k
i 1
k i

y(0)
0  (1  aT )  1
T
2T 3T 4T 5T 6T
t
Sucesión de valores de salida y(kT) con 0 < (1-aT) < 1
y(0)
(1  aT )  1
T
2T 3T 4T 5T 6T
t
Sucesión de valores de salida y(kT) con (1-aT) > 1
Resultados
Se observa que la respuesta natural de y(kT) se amortigua al aumentar
el valor de k cuando 0 < (1-aT) < 1 y vemos que la salida crece sin límite
al aumentar el valor de k cuando (1-aT) > 1.
De la ecuación de diferencias se puede concluir que el valor (1-aT) es
la raíz de la ecuación de diferencias de primer orden. También se puede
observar que el valor de esta raíz depende no sólo del coeficiente a de la
ecuación diferencial; sino además del periodo de muestreo T.
¿Cómo es la forma de la salida cuando (1  aT ) es negativo para los
casos en que su magnitud es menor que uno o mayor que uno?
En conclusión, si las magnitudes de las raíces de la ecuación de
diferencias son todas menores que 1 el sistema discreto es estable y la
estabilidad se ve afectada por el valor escogido para el periodo de
muestreo T.
Sistemas de orden superior en el
dominio del tiempo discreto
Sistema en tiempo continuo
Sea la ecuación diferencial
dny
d n 1 y
dy
d qu
d q 1u
du
an n  an 1 n 1    a1  a0 y  bq q  bq 1 q 1    b1
 b0u
dt
dt
dt
dt
dt
dt
A la cual le corresponde el siguiente modelo SISO en variables de
estado:
x  A  x  B  u
y  cT  x  d  u
Sistema en tiempo discreto
Sea la ecuación de diferencias
an y(k  n)    a1 y(k  1)  a0 y(k )  bqu(k  q)    b1 (k  1)  b0u(k )
A la cual corresponde el modelo SISO en variables de estado
x(k  1)  Ad  x(k )  Bd  u(k )
y(k )  cTd  x(k )  dd  u(k )
Note que de nuevo se ha omitido el periodo T ya que es el mismo para
todos los términos.
Derivación del modelo en tiempo discreto
a partir del modelo en tiempo continuo
Con la condición de que la entrada se mantenga constante durante la
totalidad del tiempo T:
u(t )  u(kT ) ;
para kT  t  (k  1)T
 kN
Se desea encontrar las matrices y vectores Ad, Bd, cd y dd (Cd y Dd para
MIMO)
Se parte de la ecuación de movimiento para el sistema en variables de
estado, el cual es evaluado en t = kT.
t
 At

A(t  )
x(t )  e x(0)   e
B  u( )d 
0

 t kT
A(kT  )
x(kT )  e AkT x(0)   e
B  u( )d
kT
0
para el tiempo (k+1)T se tiene:
x(( k  1)T )  e
A(k 1)T
( k 1) T
x(0) 

eA((k 1)T  )B  u( )d
0
si se descompone la parte correspondiente a kT y a T
A(( k 1)T  )
x(( k  1)T )  e AT e AkT x(0)   e
B  u( )d 
kT
0
( k 1) T


e A(( k 1)T  )B  u( )d
kT
Se observa que la parte en paréntesis rectangulares corresponde a x(kT).
kT
 AkT
 ( k 1)T A((k 1)T  )
A(kT  )
A
T
x((k  1)T )  e
x(0)   e
B  u( )d    e
B  u( )d
e

 kT
0
Si se aplica la condición de que u(t) es constante durante el intervalo T
segundos kT  t  (k  1)T , esto es u(t) = u(kT), entonces se puede sacar a
u(t) de la integral.
x(( k  1)T )  e AT x(kT ) 
( k 1) T

e A((k 1)T  )B  d  u(kT )
kT
Realizando una sustitución de variable en la integral, (k+1)T -  = p, con
d = -dp y cambiando los límites de integración se tiene:
0
Ap
x((k  1)T )  e AT x(kT )   e B  dp  u(kT )
T
Si además se aplica el signo a la integral invirtiendo los límites de
integración se obtiene:
T
x((k  1)T )  e AT x(kT )   e
0
Ap
 B  dp u(kT )
simplificando la escritura haciendo kT = k y sustituyendo la variable p de
nuevo por  tenemos (escrito para un sistema MIMO):
T
x(k  1)  e AT x(k )   e Aτ B  d  u(k )
0
y(k )  Cx(k )  D  u(k )
donde
A d  eAT
T
Bd   e Aτ B  d  A 1  A d  I B ; si A es NO singular
0
Cd  C
c d  cT
Dd  D
dd  d
Ejemplo 1: Obtener el modelo en tiempo discreto para un sistema escalar de
1er orden
x  
1
1
x  u ; x(0) = 0
T1
T1
y  ks x
x(k  1)  e
 TT
1
T
x(k )   e

1
T1

d
0
1

 
T

x(k  1)  e 1 x(k )   T1  e 1


 TT
x(k  1)  e
 TT
1
1
u (k )
T1
T
 u (k )

 T1
0
T



T1 

x( k )  1  e
 u (k )




y ( k )  k s  x( k )
donde
T1d  e
 TT
1
1
T



T1 

1  T1d  1  e




La ecuación de diferencias se obtiene al multiplicar x(k+1) por ks.
k s  x(k  1)  k s  T1d x(k )  k s  1  T1d  u(k )
agrupando se reconoce que k s  x(k  1)  y(k  1) y k s  x(k )  y(k ) por lo que se escribe
y(k  1)  T1d y(k )  k s  1  T1d  u(k )
si se pasan los términos que contienen y(k) a la izquierda
y(k  1)  T1d y(k )  k s  1  T1d  u(k )
y sustituyendo la variable k = k - 1 tenemos
y(k )  T1d y(k  1)  k s  1  T1d  u(k  1) ; y(1)  0
Ejercicio: Compare esta ecuación de diferencias con la ecuación 0 para a 
1
 5 , kS = 1 y con
T1
periodo de muestreo de T = 0.02 y de T = 0.1.
Con el modelo estático cuando u(k )  u , constante, se encuentra que no hay cambios en el
estado x por lo que:
x(k  1)  x(k )
sustituyendo
x(k )  T1d x(k )  1  T1d  u
resulta
x( k )  u
por lo que
y (k )  k s u
Ejemplo 2: Convertir a tiempo discreto el siguiente modelo (SISO) de segundo
orden
1 
0
0
k f   x(t )   1   u (t )
x (t )  
0



 M 
M

y(t )  1 0 x(t )
Donde x1 es la posición, x2 es la velocidad y u(t) es la fuerza de
manejo o de frenado aplicada a un carro. Calculamos las matrices
discretizadas Ad y Bd para este sistema; para lo cual es necesario primero
At
e
calcular la matriz de transición de estados
para la matriz A dada; para
At
1
ello usamos la definición Φ(t )  e  L ( s)
1
1 
s
1
1
kf  
Φ( s )  ( sI  A )  
k

0 s  M 
s s  f
M

Así

1
e At  


0
 kft  

 
 
M
 M  
1  e

kf 



 kft 
 


 M 
e

 kf
s  M
 0
 


1
s 
Entonces, sustituyendo t = T
A d  e AT

1



0
 kfT  
 
 
M
M
 
1  e
kf 



 kfT 
 


 M 
e

 kf  
 kf 

  T  
T 1 
 T
    
M
M 
M




   2 1  e

1

e
d


T

0 k f 
   k f k f 
Aτ



B d   e B  d  


 kf 
 k 
  T  

0
 T 1   Mf  
 
1 
 M 

1 e

d  
  e
k
 
f 
 0M
 

 
Nótese que ya que la matriz A original en tiempo continuo es singular, y se ha
realizado el proceso de encontrar la matriz Bd resolviendo directamente la integral.
Solución numérica
Si M = 1, kf = 0.1 y T = 0.1 entonces las matrices en tiempo discreto son:
1 0.0995
Ad  
,
0 0.9900
0.0050
Bd  

0.0995
El modelo en variables de estado para el sistema en tiempo discreto es:
 x1 (0.1(k  1))  1 0.0995  x1 (0.1k )  0.0050
 x (0.1(k  1))  0 0.9900   x (0.1k )  0.0995  u (0.1k )
  2

 2
 
 
 x (0.1k ) 
y (0.1k )  1 0  1

 x2 (0.1k )
El comportamiento de los sistemas
de orden superior en tiempo discreto
Sea el sistema SISO en variables de estado en tiempo discreto con x(0) = x0.
x(k  1)  Ad  x(k )  Bd  u(k )
y(k )  Cd  x(k )  Dd  u(k )
Se evalúa para valores de k desde 0 en adelante
k  0 x(1)  Ad  x(0)  Bd  u(0)
2
k  1 x(2)  A d  x(1)  Bd  u(1)  Α d  x(0)  A d Bd  u(0)  Bd  u(1)
3
2
k  2 x(3)  A d  x(2)  Bd  u(2)  A d  x(0)  A d Bd  u(0)  A d Bd  u(1)  Bd  u(2)

k 1
x(k )  Ad  x(0)  Ad Bd  u(0)    Ad Bd  u(k  2)  Bd  u(k  1)
k
k 1
x(k )  A d  x(0)   A d
k
j 0
k  j 1
Bd  u( j )
donde
Φ(k )  A d : Matriz de transición de estados discreta
k
por lo que
k 1
y(k )  c  Φ(k )  x(0)   cT  Φ(k  j  1)  Bd  u ( j )  d  u (k )
T
j 0
Conclusión
Tenemos que la respuesta total está formada por la respuesta homogénea y
la respuesta forzada.
Respuesta homogénea: c  Φ(k )  x(0)
T
k 1
c
T
Respuesta forzada:
j 0
 Φ(k  j  1)  Bd  u ( j )  d  u (k )
Representación de sistemas en t.
discr. en el dominio de la frecuencia
Propiedades de la transformada Z
Linealidad
a  u(k )  b  v(k )  a  u(k ) b  v(k )
Si
U ( z)  u(k ) y V ( z )  v(k )
entonces:
a  u(k )  b  v(k )  a  U ( z)  b  V ( z)
Desplazamiento a la derecha en el
tiempo
x( k )  X ( z )
x(k  1)  z 1 X ( z )  x(1)
x(k  2)  z 2 X ( z)  x(2)  z 1 x(1)

x(k  q)  z  q X ( z)  x(q)  z 1 x(q  1)  z 2 x(q  2)    z  q x(1)
Si x(k )  0  k = -1, -2 , -3, ... –q
entonces:
x( k  q )  z  q X ( z )
Desplazamiento a la izquierda en el
tiempo
x( k )  X ( z )
x(k  1)  z  X ( z)  x(0)  z
x(k  2)  z 2 X ( z)  x(0)  z 2  x(1)  z

x(k  q)  z q X ( z)  x(0) z q  x(1)  z q1    x(q  1)  z
Teorema del valor inicial
x(0)  lim X ( z )
z 
x(1)  limz  X ( z )  z  x(0)
z 


x(q)  lim z q X ( z )  z q x(0)  z q1 x(1)    z  x(q  1)
z 

Teorema del valor final
lim x(k )  lim ( z  1) X ( z )
k 
z 1
Relación entre la transformada Z y la transformada de Laplace
z  e sT
Función tr. del modelo en variables
de estado en tiempo discreto (MIMO)
x(k  1)  Ad  x(k )  Bd  u(k )
y(k )  Cd  x(k )  Dd  u(k )
Transformando a Z con las condiciones iniciales iguales a cero, x(0)  0
z  X( z )  A d  X( z )  Bd  U( z )
Y( z )  Cd  X( z )  Dd  U( z )
Agrupando
z  X( z )  Ad  X( z )  Bd  U( z )
z  I  Ad X( z)  Bd  U( z)
1


z

I

A
Premultiplicando por
d
X( z )  z  I  Ad  Bd  U( z )
1
Sustituyendo X(z) en la ecuación para Y(z).
Y( z )  Cd  z  I  Ad  Bd  U( z )  Dd  U( z )
1
Agrupando


Y( z )  Cd  z  I  Ad  Bd  Dd  U( z )
1
y finalmente se obtiene la función de transferencia G(z).
G( z ) 
Y( z )
1
 Cd   z  I  A d  B d  D d
U( z )