dt xd a

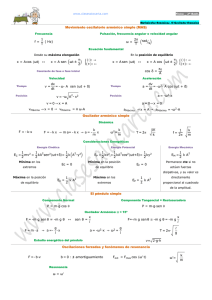
¿Cuál es la ecuación de movimiento del oscilador
armónico simple?
¿De qué depende la frecuencia de oscilación?
¿Cuál es la energía total del oscilador armónico
simple?
¿De qué depende la velocidad del oscilador
armónico simple?
A partir de la 2ª Ley de Newton se tiene que:
Por otro lado, la fuerza de restitución de un
oscilador armónico simple es (Ley de Hooke):
Igualando ambos términos:
m  a  k  x
Como la aceleración está dada por:
La ecuación de movimiento es:
2
d x k
 x0
2
dt
m
2
d x
a 2
dt
http://en.wikipedia.org/wiki/File:Muelle.gif
F  m a
F  k  x
Una posible solución a la ecuación de movimiento es:
x(t )  A cos( t   )
La primera y segunda derivadas con respecto al tiempo son:
2
dx
d
x
  A sin( t   ) 2   2 A cos( t   )
dt
dt
Sustituyendo:
2
2
d x
d x
2
2
  x 
 x  0
2
2
dt
dt
Por lo tanto la frecuencia de oscilación es:
k
k
 
 
m
m
2
El oscilador armónico es un sistema conservativo, por lo tanto,
la fuerza se puede escribir como:
dU
F 
dx
Por otro lado, sabemos que la fuerza está dada por la Ley de
Hooke, por lo tanto:
dU
kx  
dx
La energía potencial en este caso es:
U U0   k  x  k  x
1
2
2
La energía total del sistema es:
ET  K  U  m  v  k  x
2
1
2
1
2
2
En los puntos de retorno se tiene que :
x  xm  A; v  0  K  0
ET  k  A
2
1
2
Igualando ambas ecuaciones:
1
2
k  A  mv  k  x
2
2
1
2
1
2
2
Por lo tanto, la velocidad del oscilador es:
v
k
m
A
2
x
2
   A
2
x
2

-xm
xm
http://upload.wikimedia.org/wikipedia/commons/thumb/2/22/
Harmonic_oscillator.svg/250px-Harmonic_oscillator.svg.png
1. La combinación bloque-resorte que se
muestra en la figura se estira en
k = 310 N/m
dirección positiva x una distancia de
m = 150 g
11.6 cm del equilibrio y luego se suelta.
a) ¿Cuál
es
la
energía
total
almacenada en el sistema?
b) ¿Cuál es la velocidad máxima del
bloque?
c) ¿Cuál es la aceleración máxima?
d) Si el bloque se suelta en t=0, ¿cuáles
son
su
posición,
velocidad
aceleración en t=0.215?
y
-xm
xm
http://upload.wikimedia.org/wikipedia/commons/thumb/2/22/
Harmonic_oscillator.svg/250px-Harmonic_oscillator.svg.png
2. Un oscilador consta de un bloque de
512 g de masa unido a un resorte.
Cuando es puesto en oscilación con una
amplitud de 34.7 cm, se observa que
repite su movimiento cada 0.484
segundos. Halle:
a) El periodo
b) La frecuencia
c) La frecuencia angular
d) La constante de fuerza del resorte
e) La velocidad máxima
f) La energía total del sistema
-xm
xm
http://upload.wikimedia.org/wikipedia/commons/thumb/2/22/
Harmonic_oscillator.svg/250px-Harmonic_oscillator.svg.png
3. Un objeto de 1.26 kg de masa unido a
un resorte de 5.38 N/cm de constante
de
fuerza
se
pone
en
oscilación
estirando el resorte 26.3 cm y dando al
objeto una velocidad de 3.72 m/s hacia
la posición de equilibrio del resorte.
Calcule:
a) El ángulo de fase del movimiento
armónico simple resultante.
b) Calcule la amplitud del movimiento
-xm
xm
http://upload.wikimedia.org/wikipedia/commons/thumb/2/22/
Harmonic_oscillator.svg/250px-Harmonic_oscillator.svg.png