El Cálculo. Louis Leithold. Séptima edición en español
Anuncio

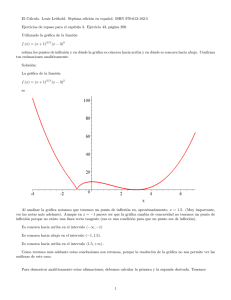
El Cálculo. Louis Leithold. Séptima edición en español. ISBN 970-613-182-5 Ejercicios de repaso para el capítulo 3. Ejercicio 35, página 290. (a) Determina los extremos relativos de la función f (x) = (1 (x 3 x) 3 1) x 1 . x>1 (b) Obten los valores de x en los que ocurren los extremos relativos. (c) Obten los intervalos en los que f es creciente. (d) Obten los intervalos en los que f es decreciente. (e) Halla los puntos de in‡exión de la grá…ca de f . (f) Determina en dónde la grá…ca de la función f es cóncava hacia arriba. (g) Determina en dónde la grá…ca de la función f es cóncava hacia abajo. Dibuja la grá…ca de la función a partir de las respuestas de los incisos (a)-(g). Solución: (a) Determina los extremos relativos de la función f (x) = (1 (x 3 x) 3 1) x 1 . x>1 Primero debemos determinar los puntos críticos de la función. Los puntos críticos son los números reales en los cuales la derivada de la función se anula. La derivada es 2 3 (1 x) 2 3 (x 1) f 0 (x) = x 1 x>1 Veamos cuando se anula. Primero, si 3 (1 2 x) = 0 la solución es 1. Para el segundo segmento, tenemos 3 (x 2 1) = 0, cuya solución es 1, que es un valor de x que no se encuentra en el dominio de este segmento de la función. En resumen, la derivada de la función se anula únicamente en x = 1. El único punto crítico es x = 1. En ese punto crítico tenemos que la función vale 0; es decir, f (1) = 0 (b) Obtenga los valores de x en los que ocurren los extremos relativos. En el inciso anterior determinamos que el único punto crítico es x = 1. Para determinar de qué tipo de punto crítico se trata, utilizamos el Teorema 3.4.4 del libro (3.4.4 Teorema Criterio de la primera derivada para extremos relativos, página 225) que establece que si f 0 (x) < 0 para todos los valores de x en un intervalo abierto que contenga a c como su extremo derecho, y si f 0 (x) > 0 para todos los valores de x de algún intervalo abierto que contenga a c como su extremo izquierdo, entonces f tiene un valor mínimo relativo en c. 1 Como 2 f 0 (x) = 3 (1 x) 2 3 (x 1) x 1 x>1 es claro que a la izquierda de 1 tenemos que f 0 (x) < 0 y que a la derecha de 1 tenemos f 0 (x) > 0, así que x = 1 es un mínimo relativo de la función. Así que el punto x = 1 es un mínimo relativo y el valor del mínimo es 0. Notese que en este caso f 00 (1) = 0 y el punto x = 1 es un mínimo y no un punto de in‡exión. (c) Los intervalos en los que f es creciente. La función es creciente cuando la derivada es positiva y es decreciente cuando la derivada es negativa. En este caso la derivada es 2 f 0 (x) = 3 (1 x) 2 3 (x 1) x 1 x>1 y es claro que para x > 1 tenemos f 0 (x) > 0, así que la función es creciente en el intervalo (1; +1). (d) Los intervalos en los que f es decreciente. La función es creciente cuando la derivada es positiva y es decreciente cuando la derivada es negativa. En este caso la derivada es 2 f 0 (x) = 3 (1 x) 2 3 (x 1) y es claro que para x x 1 x>1 1 tenemos f 0 (x) < 0, así que la función es decreciente en el intervalo ( 1; 1). (e) Halla los puntos de in‡exión de la grá…ca de f . Para determinar los puntos de in‡exión de la grá…ca debemos determinar en qué puntos la segunda derivada de la función existe y en qué puntos que sí existe es nula. La segunda derivada es f 0 (x) = 6 (1 6 (x x) x 1 1) x > 1 Como f 00 (x) existe para todos los valores de x, el único punto de in‡exión posible de f ocurre donde f 00 (x) = 0. Eso sucede únicamente cuando x = 1. Para determinar si x = 1 es un punto de in‡exión debemos veri…car si f 00 (x) cambia de signo ahí. Calculamos el valor de la función a la izquierda de x = 1, digamos en 0.9; tenemos f 00 (0:9) = 6 (1 0:9) = 0:6. Ahora a la derecha de x = 1, digamos en 1:1; tenemos f 00 (1:1) = 6 (1:1 1) = 0:6. Así que la segunda derivada no cambia de signo y x = 1 no es un punto de in‡exión. Resumiendo, la grá…ca no tiene puntos de in‡exión. (f) Determina en dónde la grá…ca de la función f es cóncava hacia arriba. Una función es concava hacia arriba en un punto c si la función es diferenciable en un intervalo abierto que contiene a c y si f 00 (c) > 0. La segunda derivada de la función es 2 f 00 (x) = 6 (1 6 (x x) x 1 1) x > 1 que evidentemente siempre es mayor que cero. Así que la función es concava hacia arriba en todo el eje real. (g) Determina en dónde la grá…ca de la función f es cóncava hacia abajo. En el inciso anterior demostramos que la función es concava hacia arriba en todo el eje real, así que en ningún lugar es concava hacia abajo. Dibuja la grá…ca de la función a partir de las respuestas de los incisos (a)-(g). A continuación presentamos la grá…ca de la función, que ha sido trazada tomando en cuenta todos los resultados analíticos obtenidos en los incisos (a)-(g), f(x) 6 5 4 3 2 1 -1.0 -0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 x En la siguiente grá…ca presentamos la zona del mínimo relativo con mayor resolución, f(x) 0.002 0.001 0.000 0.92 0.94 0.96 0.98 1.00 1.02 1.04 1.06 -0.001 Ahora presentamos la grá…ca de la derivada 3 1.08 1.10 x f'(x) 6 5 4 3 2 1 -1.0 -0.5 0.5 1.0 1.5 2.0 2.5 -1 -2 -3 -4 -5 Y …nalmente presentamos la grá…ca de la segunda derivada f''(x) 6 5 4 3 2 1 -1 1 2 3 x -1 -2 -3 -4 -5 4 3.0 x