INTEGRAL IMPROPIA

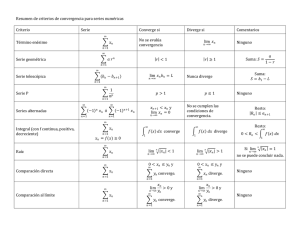
Cálculo II (0252)
Semestre 1-2011
TEMA 3
INTEGRAL
IMPROPIA
Semestre
1-2011
José Luis Quintero
Junio 2011
Departamento de
Matemática Aplicada
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252)
Prof.
José Luis Quintero
Las notas presentadas a continuación tienen como único fin, el de prestar apoyo al
estudiante y facilitar su entendimiento en el tema de la integral impropia.
La guía contempla un pequeño resumen de la teoría correspondiente que sirve de
repaso a los contenidos teóricos que componen el tema. Se presentan ejercicios resueltos y
propuestos, algunos son originales, otros se han tomado de guías redactadas por profesores,
también hay ejercicios tomados de exámenes y de algunos textos. Se ha tratado de ser lo
más didáctico posible y se espera prestar un apoyo a la enseñanza del Cálculo II en
Ingeniería.
Agradezco las observaciones y sugerencias que me puedan hacer llegar en la mejora
del presente material, las mismas pueden ser enviadas a la siguiente dirección de correo:
[email protected].
INDICE GENERAL
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252)
Departamento de
Matemática Aplicada
Prof.
José Luis Quintero
TEMA 3. INTEGRAL IMPROPIA
3.1.
La integral impropia
151
3.2.
Integrales con integrandos no acotados
151
3.3.
Integrales con intervalos de integración de longitud infinita
154
3.4.
Criterios de convergencia
156
3.5.
Ejercicios resueltos
159
3.6.
Ejercicios propuestos
163
G
LA INTEGRAL IMPROPIA
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252) – TEMA 3
Integral Impropia
Pág.: 151 de 170
Prof.
José Luis Quintero
3.1. LA INTEGRAL IMPROPIA
Anteriormente se afirmó que si la función f(x) es continua y positiva en el intervalo
[a,b] con a y b finitos,
∫
b
f(x)dx
a
representa el área bajo la curva, usando el Teorema Fundamental del Cálculo para poder
obtener su valor numérico. Sin embargo, en muchas aplicaciones, físicas o matemáticas, se
formulan integrales donde no se cumplen ciertas condiciones expuestas anteriormente. A
continuación se describen algunas de ellas:
a. El integrando f(x) es tal que lim f(x) = ±∞ con r ∈ [a,b] , tomando límite lateral de ser el
x →r
caso. Es decir el integrando es una función no acotada.
b. El intervalo de integración no es finito, por ejemplo: [a, +∞) , (−∞, a] o bien (−∞, +∞) .
Las integrales con alguna de las condiciones anteriores se conocen con el nombre de
integrales impropias. En general, la técnica es transformar la integral impropia en un límite
con una integral definida sobre un intervalo finito donde se pueda aplicar el Teorema
Fundamental del Cálculo.
3.2. INTEGRALES CON INTEGRANDOS NO ACOTADOS
CASO 1. Si f(x) es continua en [a,b) y lim f(x) = ±∞ , entonces (ver figura 1)
x → b−
∫
b
f(x)dx = lim
r →b −
a
∫
r
f(x)dx .
a
CASO 2. Si f(x) es continua en (a,b] y lim f(x) = ±∞ , entonces (ver figura 2)
x → a+
INTEGRALES CON
INTEGRANDOS NO ACOTADOS
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252) – TEMA 3
∫
b
f(x)dx = lim
r → a+
a
∫
Integral Impropia
Pág.: 152 de 170
Prof.
José Luis Quintero
b
f(x)dx
r
Figura 1. Gráfica del caso 1
Figura 2. Gráfica del caso 2
CASO 3. Si f(x) es continua en [a,b] excepto en r ∈ (a,b) , donde se tiene lim f(x) = ±∞ ,
x →r
entonces
∫
b
f(x)dx =
a
∫
r
f(x)dx +
a
∫
b
f(x)dx
r
En los casos 1 y 2, si los límites existen y son finitos se dirá que la integral impropia
de la izquierda converge, en caso contrario divergen. En el caso 3, si las integrales impropias
de la derecha convergen ambas se dirá que la integral impropia de la izquierda converge; si
alguna de las integrales impropias de la derecha diverge se dirá que la integral impropia de la
izquierda diverge.
A continuación se dan algunos ejemplos:
INTEGRALES CON
INTEGRANDOS NO ACOTADOS
U.C.V.
F.I.U.C.V.
Integral Impropia
Pág.: 153 de 170
Prof.
José Luis Quintero
CÁLCULO II (0252) – TEMA 3
Ejemplo 1. Calcule la siguiente integral impropia (o determine su divergencia).
4
∫
dx
(1 − x)2 / 3
0
Solución.
∫
4
dx
=
(1 − x)
2 /3
0
∫
1
dx
(1 − x)
2 /3
0
∫
+
4
dx
(1 − x)
2 /3
1
= lim
c →1−
c
= lim (−33 1 − x) + lim (−33 1 − x)
c →1−
c →1+
0
4
c
∫
c
dx
(1 − x)
2 /3
0
+ lim
c →1+
∫
4
c
dx
(1 − x)2 /3
= lim (−33 1 − c + 3) + lim (−33 −3 + 33 1 − c)
c →1−
c →1+
= 3 + 3 3 = 3(1 + 3)
3
3
Ejemplo 2. Calcule la siguiente integral impropia (o determine su divergencia).
∫
1
dx
1 − x2
0
Solución.
∫
1
0
dx
1−x
2
= lim
c →1−
∫
c
dx
c
1−x
2
0
= lim arcsen(x) 0 = lim (arcsen(c) − 0) =
c →1−
c →1−
π
2
.
Ejemplo 3. Calcule la siguiente integral impropia (o determine su divergencia).
∫
1
dx
e − e− x
x
0
Solución.
∫
∫
ex
2x
e
−1
dx =
∫
dx
ex − e − x
du
u −1
2
=−
=
∫
ex
e2x − 1
dx .
1 1+u
1 1 + ex
ln
+ C = − ln
+C
2 1−u
2 1 − ex
.
(u = ex ⇒ du = ex dx)
Se tiene entonces:
∫
1
dx
e −e
x
0
−x
= lim
c → 0+
∫
1
dx
e −e
x
c
−x
1 1 + ex
= lim − ln
2 1 − ex
c → 0+
o+
1
c
 1 1 + e 1 1 + ec
= lim  − ln
+ ln
c
c → 0+ 
 2 1−e 2 1−e
+
1 1+e 1 1+ e
1 1 + e 1 1 + eo
= − ln
+ ln
=
−
ln
+ ln
2 1 − e 2 1 − e0+
2 1 − e 2 1 − e0+
=−
1 1 + e 1 1 + 1+
1 1 + e 1 2+
1 1+e
ln
+ ln
= − ln
+ ln
= − ln
+∞
+
2 1− e 2 1−1
2 1 − e 2 0−
2 1−e
Por lo tanto la integral diverge.




INTEGRALES CON INTERVALOS DE
INTEGRACIÓN DE LONGITUD INFINITA
U.C.V.
F.I.U.C.V.
Integral Impropia
Pág.: 154 de 170
Prof.
José Luis Quintero
CÁLCULO II (0252) – TEMA 3
3.3. INTEGRALES CON INTERVALOS DE INTEGRACIÓN
DE LONGITUD INFINITA
CASO 1. Si f(x) es continua en [a, +∞) entonces
∫
+∞
∫
f(x)dx = lim
c →+∞
a
c
f(x)dx
a
CASO 2. Si f(x) es continua en (−∞, a] entonces
∫
a
f(x)dx = lim
c →−∞
−∞
∫
a
f(x)dx
c
CASO 3. Si f(x) es continua en (−∞, +∞) entonces
∫
+∞
f(x)dx =
−∞
∫
a
f(x)dx +
−∞
∫
+∞
f(x)dx
a
En los casos 1 y 2, si los límites existen y son finitos se dirá que la integral impropia
de la izquierda converge, en caso contrario diverge. En el caso 3, si las integrales impropias
de la derecha convergen ambas se dirá que la integral impropia de la izquierda converge en
caso contrario diverge.
A continuación se dan algunos ejemplos:
Ejemplo 4. Calcule la siguiente integral impropia (o determine su divergencia).
∫
+∞
-∞
arctg(x)
x2 + 1
dx
Solución.
∫
+∞
arctg(x)
x +1
2
-∞
dx =
∫
0
arctg(x)
x +1
2
-∞
= lim
c →−∞
∫
0
c
dx +
arctg(x)
x2 + 1
(arctg(x))2
= lim
c →−∞
2
∫
+∞
0
arctg(x)
x2 + 1
dx + lim
c →+∞
0
c
∫
dx
+∞
0
arctg(x)
x2 + 1
(arctg(x))2
+ lim
c →+∞
2
c
=−
0
dx
π2 π2
+
=0
8
8
INTEGRALES CON INTERVALOS DE
INTEGRACIÓN DE LONGITUD INFINITA
U.C.V.
F.I.U.C.V.
Integral Impropia
Pág.: 155 de 170
Prof.
José Luis Quintero
CÁLCULO II (0252) – TEMA 3
Ejemplo 5. Calcule la siguiente integral impropia (o determine su divergencia).
∞
∫
(1 − x)e− x dx
1
Solución.
lim
b → +∞
∫
b

b
(1 − x)e dx = lim  −(1 − x)e−x −
1
b →+∞ 

−x
1
∫
b
1

b

e− x dx  = lim  −(1 − b)e−b + e− x 
1
 b →+∞ 

u = 1 − x ⇒ du = −dx , dv = e−x dx ⇒ v = −e− x
1
= lim  −(1 − b)e−b + e−b − e−1  = lim be−b − e−1  = −
 b →+∞ 

b →+∞ 
e
Ejemplo 6. Calcule la siguiente integral impropia (o determine su divergencia).
∫
∞
0
dx
x(x + 1)
Solución.
∫
∫
∞
dx
x(x + 1)
0
dx
x(x + 1)
(u =
lim
a → 0+
∫
∫
=2
x ⇒ du =
∫
1
a
1
dx
=
x(x + 1)
0
du
u2 + 1
dx
2 x
dx
x(x + 1)
+
∫
∞
1
dx
x(x + 1)
= 2arctg(u) + C = 2arctg( x) + C
)
+ lim
b →+∞
∫
b
1
dx
1
b
= lim 2arctg( x) + lim 2arctg( x)
 a b →+∞ 
1
x(x + 1) a→ 0+ 
π
π
π
lim 2arctg(1) − 2arctg(a) + lim 2arctg(b) − 2arctg(1) = 2. − 0 + 2. − 2. = π
b →+∞
4
2
4
a → 0+
CRITERIOS DE
CONVERGENCIA
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252) – TEMA 3
Integral Impropia
Pág.: 156 de 170
Prof.
José Luis Quintero
3.4. CRITERIOS DE CONVERGENCIA
El estudio de la convergencia de integrales impropias por vía del límite requiere del
cálculo de una primitiva y no siempre es factible o fácil su cálculo; existe la alternativa de
comparación con otras integrales impropias de las cuales se conoce su comportamiento.
TEOREMA 1. (Criterio de comparación simple). Sean f(x) y g(x) funciones continuas y
tales que 0 ≤ f(x) ≤ g(x) en [a, +∞) .
a. Si
b. Si
∫
∫
+∞
g(x)dx converge entonces
a
+∞
∫
f(x)dx diverge entonces
a
∫
+∞
f(x)dx converge.
a
+∞
g(x)dx diverge.
a
Ejemplo 7. Estudie la convergencia de
∫
+∞
2
e− x dx .
1
Solución.
Si x ∈ 1, +∞ ) se tiene x2 > x y e− x < e− x por ser e− x una función decreciente. Por otro lado
2
la integral
∫
+∞
e− x dx = lím
c →+∞
1
∫
c
1
1 1

e− x dx = lím  −e −c +  =
c → +∞ 
e e
es convergente, luego por el criterio de comparación la integral
∫
+∞
2
e− x dx
1
converge.
TEOREMA 2. (Criterio de comparación por paso al límite). Sean f(x) y g(x) funciones
continuas no negativas en [a, +∞) con g(x) ≠ 0 .
a. Si
f(x)
=L ≠0
x →+∞ g(x)
lím
entonces las integrales
∫
+∞
f(x)dx y
a
∫
+∞
g(x)dx convergen o divergen ambas.
a
CRITERIOS DE
CONVERGENCIA
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252) – TEMA 3
Integral Impropia
Pág.: 157 de 170
Prof.
José Luis Quintero
b. Si
lím
x →+∞
y
∫
+∞
∫
g(x)dx converge entonces
a
f(x)
=0
g(x)
+∞
f(x)dx converge.
a
c. Si
lím
x →+∞
y
∫
+∞
g(x)dx diverge entonces
a
∫
f(x)
=∞
g(x)
+∞
f(x)dx diverge.
a
Ejemplo 8. Estudie la convergencia de
∫
+∞
1
xp
1
dx, p > 0 .
Solución.
∫
+∞
1
1
xp
dx = lím
c →+∞
∫
c
1
c
 c1−p
x1 −p
1 
1
dx
lím
=
lím
=
−

=
p
c
→
+∞
c
→+∞
1−p
x
1 − p 1 − p  p − 1
1
1
p ≠1
p >1
Si p = 1 se tiene que
∫
+∞
1
1
dx = lím
c →+∞
x
∫
c
1
c
1
dx = lím ln x = lím ln c = +∞
1
c
→+∞
c → +∞
x
Por lo tanto
∫
+∞
1
1
xp
dx
converge a
1
p −1
Si p > 1 .
Ejemplo 9. Estudie la convergencia de
∫
Solución.
Considere la integral
+∞
1
2 + ln(x)
x
dx .
CRITERIOS DE
CONVERGENCIA
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252) – TEMA 3
∫
+∞
1
x2 /3
1
dx
que diverge porque p < 1 . Se tiene
2 + ln(x)
f(x) =
x
>0
y
1
g(x) =
x
en 1, +∞ ) . De modo que
2 + ln(x)
x
1
x →+∞
x2 /3
>0
2 /3
= lím x1/6 (2 + ln(x)) = +∞ ,
lím
x → +∞
luego por la parte c del teorema 2 la integral
∫
+∞
2 + ln(x)
x
1
dx
diverge.
Ejemplo 10. Estudie la convergencia de
∫
+∞
1
x + x3
4
1
dx .
Solución.
Siendo
1
f(x) =
x +x
que son continuas y positivas en 1, +∞ ) se tiene
4
3
y g(x) =
1
x4 + x3
1
x → +∞
x4
lím
= 1.
Puesto que
∫
+∞
1
x4
1
dx
converge se tiene por la parte a del teorema 2
∫
converge.
+∞
1
x + x3
4
1
dx
1
x4
Integral Impropia
Pág.: 158 de 170
Prof.
José Luis Quintero
EJERCICIOS RESUELTOS
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252) – TEMA 3
Integral Impropia
Pág.: 159 de 170
Prof.
José Luis Quintero
3.5. EJERCICIOS RESUELTOS
1. Para un cierto valor real C, la integral dada por
+∞
∫
2
1 
 Cx
−
 2
 dx
 x + 1 2x + 1 
converge. Determine el valor de C y calcúlela.
Solución.
+∞
∫
2
a
∫
1 
 Cx
−
 2
 dx = alim
→+∞
 x + 1 2x + 1 
2
a
1 
1
 Cx
C

−
dx = lim  ln(x2 + 1) − ln(2x + 1) 
 2

a→ +∞  2
2
 x + 1 2x + 1 
2
 (x2 + 1)C
1
= lim .ln 
 2x + 1
a →+∞ 2

Para que converja c =
1
2
a
  (a2 + 1)C

1
 = . lim  ln 

 2 2 a→+∞   2a + 1

 5C
 − ln 

 5

 


. Asi se tiene que
  a2 + 1 
 5  1   1 
 5  1   1 
 1  1  5 
1
 = .  ln
 − ln 
. lim  ln 
− ln 
 = .  ln   − ln 


 .
  = ln 


 5  2   2 
 5  2
2 a→ +∞   2a + 1 
2
2
2
5















 

2. Determine k para que la integral
∫
1
xk ln(x)dx
0
sea convergente.
Solución.
∫
1
1
xk ln(x)dx =
xk +1
1
ln(x) −
k +1
k +1
0
0
u = ln(x) ⇒ du =
dx
x
∫
1
xk dx
0
, dv = x dx ⇒ v =
k
xk +1
k +1
 k +1
c
xk +1
lím
x ln(x)dx = lím  −
ln(c) −
(k + 1)2
c → 0+
c → 0+  k + 1
c

Si k + 1 > 0 ⇒ k > −1 :
∫
1
k
∫
1
 k +1
1
ck +1 
 = − lím  c
ln(c) +
−


(k + 1)2 (k + 1)2 
c → 0+ 
k + 1
c
1
xk ln(x)dx = −
0
1
(k + 1)2
.
Integral Impropia
Pág.: 160 de 170
EJERCICIOS RESUELTOS
U.C.V.
F.I.U.C.V.
Prof.
José Luis Quintero
CÁLCULO II (0252) – TEMA 3
3. Si f(t) es continua para t ≥ 0 , la transformada de Laplace es la función F definida por
∞
∫
F(s) =
f(t)e −st dt .
0
Halle la transformada de Laplace de las funciones:
a.
f(t) = tn. (n ∈ N)
Solución.
F(s) =
∫
∞
n − st
t e
dt = lím
c →+∞
0
=
∫
n
lím
s c →+∞
c
n − st
t e
0
∫
 −st n
e t
dt = lím  −
c →+∞ 
s

n(n − 1)
s2
0
n
+
s
∫
c
0

tn −1e−st dt 


c
tn −1e−st dt , s > 0 , n = 1, 2,...
0
 −st n −1
n
e t
= lím  −
s c →+∞ 
s

=
c
lím
c → +∞
∫
c
+
0
n −1
s
∫
c
0

tn − 2e −st dt  , s > 0 , n = 1,2,...


c
tn − 2e−st dt , s > 0 , n = 1, 2,...
0
⋮
=
n!
lím
sn c → +∞
∫
c
e−st dt =
0
n! 1
n!
. = n +1 , s > 0 , n = 1, 2,...
n s
s
s
n −1
(u = t ⇒ du = nt
n
dt , dv = e−st dt ⇒ v = − 1s e−st )
(u = tn −1 ⇒ du = (n − 1)tn − 2dt , dv = e−st dt ⇒ v = − 1s e−st )
b.
0 0 ≤ t < a
U(t − a) = 
. (función escalón unitario)
t≥a
1
Solución.
F(s) =
∫
∞
U(t − a)e
0
− st
dt =
∫
∞
e
− st
dt = lím
c →+∞
a
∫
c
e
−st
a
−cs
 e
= lím  −
c → +∞ 
s

e−st
dt = lím −
c → +∞
s
−
e
− as
− as
 e
=
s 
s
4. La definición por integral de la función gamma, viene dada por
Γ(x) =
Pruebe que:
a. La integral converge para x > 0 .
Solución.
∫
∞
t x −1e− t dt .
0
c
a
, s>0
EJERCICIOS RESUELTOS
U.C.V.
F.I.U.C.V.
∫
t
x −1 − t
e dt = lím
0
Prof.
José Luis Quintero
CÁLCULO II (0252) – TEMA 3
∞
c → +∞
∫
c
t
0
Integral Impropia
Pág.: 161 de 170
c
 x −1 c

t
e dt = lím  − t
t x − 2e− t dt 
+ (x − 1)
c →+∞ 

e 0
0


c
c
 x −1
 x −1 − t
t
t e
1
= lím  − t
+ (x − 1) 
+

c →+∞
 x −1
x −1
e 0
0


∫
x −1 − t
∫
c
0

t x −1e−t dt  

 
(u = tx −1 ⇒ du = (x − 1)t x −2 dt , dv = e−t dt ⇒ v = −e−t )
(u = e−t ⇒ du = −e− t dt , dv = t x − 2dt ⇒ v =
b.
t x −1
)
x −1
Γ(x + 1) = xΓ(x) .
Solución.
Γ(x + 1) =
c.
∫
∞
x −t
x −t
t e dt = t e
0
∞
0
+x
∫
∞
t x −1e− t dt = lím
c →+∞
0
cx
ec
+ xΓ(x) = xΓ(x) , x > 0
(u = t x ⇒ du = xt x −1dx , dv = e−t dt ⇒ v = −e− t )
Γ(n + 1) = n! .
Solución.
Γ(1) =
∫
∞
e− t dt = −e− t
0
∞
0
= 1.
Aplicando la propiedad anterior se tiene:
x = 1 ⇒ Γ(1 + 1) = 1.Γ(1) = 1.1 = 1 ⇒ Γ(2) = 1!
x = 2 ⇒ Γ(2 + 1) = 2.Γ(2) = 2.1 = 2 ⇒ Γ(3) = 2!
x = 3 ⇒ Γ(3 + 1) = 3.Γ(3) = 3.2 = 6 ⇒ Γ(4) = 3!
⋮
Γ(n + 1) = n!
5. Estudie la convergencia de
∫
+∞
1
x
1

1 + x  dx .


Solución.
Se hace uso del criterio de comparación por paso al límite parte a:
Considere las funciones
2
x
1
1


g(x) =  1 +  y f(x) =  1 + 
x
x


en el intervalo 1, +∞ ) donde ambas son continuas y positivas. De modo que
x
1

1 + x 
 = e =e
lím 
2
x →+∞
1
1

1
+


x

EJERCICIOS RESUELTOS
U.C.V.
F.I.U.C.V.
CÁLCULO II (0252) – TEMA 3
Por otro lado
∫
+∞
1
2
1

1 + x  dx


diverge, lo cual puede ser comprobado fácilmente, luego la integral
∫
+∞
1
x
1

1 + x  dx


diverge.
6. Utilice el teorema de comparación para determinar si la integral
∫
π /2
0
1
dx
x.sen(x)
es convergente o divergente.
Solución.
Si x ∈ 0, 2π  se tiene que sen(x) ≤ 1 , de modo que x.sen(x) ≤ x . Luego
(
1
1
≥
x.sen(x) x
Por otro lado
∫
π /2
0
1
dx = lím
x
c → 0+
∫
π /2
c
1
π /2
dx = lím ln(x) c = +∞
+
x
c→0
Por el teorema de comparación parte c la integral
∫
diverge.
π /2
0
1
dx
x.sen(x)
Integral Impropia
Pág.: 162 de 170
Prof.
José Luis Quintero
Integral Impropia
Pág.: 163 de 170
EJERCICIOS PROPUESTOS
U.C.V.
F.I.U.C.V.
Prof.
José Luis Quintero
CÁLCULO II (0252) – TEMA 3
3.6. EJERCICIOS PROPUESTOS
1. Verifique las siguientes afirmaciones:
1.1.
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
1
dx
x
0
1.3.
3
∞
0
1.11.
1.13.
1.15.
1.17.
1.19.
1.21.
1.23.
dx
1+ x
12
1.6.
=π
1.8.
dx
(diverge)
x ln(x)
arctg(x)
x +1
2
dx
x +1
3
0
∞
=
dx =
π2
8
2π
3 3
1
e sen(x)dx =
2
−x
0
∞
xe
− x2
1
4
x − 5x + 4
∞
xe
0
1
dx =
2e
x −2
2
2
dx
=1
x2
−2x
dx
dx (diverge)
1
dx =
4
x + 4x + 9
2
−∞
0
∞
∞
1
ctg(x)dx (diverge)
0
sen(x)dx (diverge)
0
π2
∞
1.4.
∞
∞
2
−∞
1.9.
(diverge)
dx
(diverge)
x
∞
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
dx
(diverge)
x
−1
(x − 1)2
1
1.7.
1.2.
dx
0
1.5.
=2
2
12
1.10.
dx
2
x(ln(x))
0
∞
1.12.
dx
=
1 1
+ ln(3)
3 4
(x − 1)
1
2
dx
(diverge)
x − 5x2
3
0
∞
dx
1.18.
x + 2x + 2
2
−∞
1
1.20.
dx
e − e− x
x
0
∞
1.22.
1
1
1.24.
0
1
ln(2)
(k > 0)
2
1.16.
=
1
k
∞
2
5
e−kx dx =
0
1.14.
π
=
=π
(diverge)
1 
 x
(x − 1)  2
− 2  dx (diverge)
x +1 x 
dx
1 − x2
=
π
2
Integral Impropia
Pág.: 164 de 170
EJERCICIOS PROPUESTOS
U.C.V.
F.I.U.C.V.
Prof.
José Luis Quintero
CÁLCULO II (0252) – TEMA 3
2. Encuentre a > 0 tal que
2
∫
a
dx
1+ x
2
0
=
∫
∞
a
dx
1 + x2
.
3. Determine todos los posibles valores de q para los cuales la integral
∫
1
xqdx
0
converge.
Rta. Converge a
1
si q > −1 .
q+1
4. Determine el valor de n para el cual la integral impropia
∫
∞
1
 nx2
1 
−
 3
 dx
 x + 1 3x + 1 
es convergente, y evalúe la integral para este valor de n.
Rta. n =
1
3
y la integral converge a
5. Determine si la integral
∫
2
0
dx
x −1
converge o diverge, en caso de ser convergente, calculela.
6. Halle a y b tal que
∫
+∞
1
 2x2 + bx + a

− 1  dx = 1 .


 x(2x + a)

1
ln( 31 )
3
− 13 ln(
32
4
).