Problema - 1.09-22

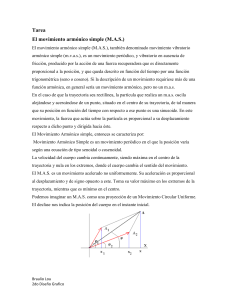
MECÁNICA
aletos
MOVIMIENTO VIBRATORIO ARMÓNICO
Física para Ciencias e Ingeniería
1
Contacto: [email protected]
Esta
que esfijas
igual
una constante
precedidauna
por distancia
un signo 2s,
negativo,
multiplicada
por el desplazaDosaceleración,
cargas positivas
de acarga
q1 están separadas
y una ytercera
carga positiva
móvil, de
miento,
es
del
tipo,
carga q y masa m, está situada a una distancia s de cada una de ellas.
que si la carga positiva móvil se desplaza[3]una distancia muy pequeña de su posición de equilia =-Demuéstrese
~2 x
brio, efectúa un movimiento vibratorio armónico de periodo:
T=r
ms 3
k q1 q
SOLUCIÓN:
La fuerza de repulsión entre las cargas q1 y q, separadas una distancia r, es:
F=k
q1 q
r2
[1]
Si la carga positiva q se desplaza una distancia x de la posición de equilibrio, queda sometida, por parte de las
cargas q1, a las fuerzas de repulsión:
q1 q
F1 = k
(s + x) 2
[2]
q1 q
F2 = k
(s - x) 2
La fuerza resultante, dirigida hacia la posición de equilibrio, es:
q1 q
q1 q
(s - x) 2 - (s + x) 2
1
1
k
=
k
q
q
=
k
q
q
=
&
#
1
1
(s + x) 2
(s - x) 2
(s + x) 2 (s - x) 2
(s + x) 2 (s - x) 2
(s 2 - 2sx + x 2) - (s 2 + 2sx + x 2)
- 4sx
- 4sx
= k q1 q
= k q1 q 2
= k q1 q 4
2
2 2
s
2
s2 x2 + x4
!(s + x) (s - x)$
!s - x $
F = F1 - F2 = k
[3]
Si la distancia x es muy pequeña, x4 y x2 son despreciables frente a s4, y por consiguiente, la fuerza [3] queda en
la forma:
- 4sx
4x
[4]
F = k q1 q
=- k q 1 q 3
s4
s
Aplicando la ecuación de la dinámica, y despejando la aceleración:
F = ma
4x
- k q 1 q 3 = ma
s
4 k q1 q
a =x
ms 3
[4]
Esta aceleración, que es igual a una constante precedida por un signo negativo, y multiplicada por el desplazamiento x, es del tipo,
a =- ~ 2 x
[5]
que es característica de todo movimiento vibratorio armónico.
[Véase la fórmula 9.10 del epígrafe 9.4 del Capítulo 1.09]
b) Igualando los segundos miembros de [4] y [5], y despejando la frecuencia angular:
~=2
k q1 q
ms 3
[6]
Por otra parte, la frecuencia angular ~ es:
~=
2r
T
b) Igualando los segundos miembros de [6] y [7], y despejando el periodo:
T=r
ms 3
k q1 q
[7]