to get the file
Anuncio

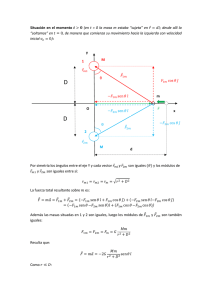
CAPITULO 4. ECUACIONES DIFERENCIALES DE PRIMER ORDEN 4.1. Introducción Se denomina ecuación diferencial ordinaria a toda ecuación en la que aparecen una o varias derivadas de una función. Cuando las derivada que aparecen en una ecuación diferencial son derivadas totales, la ecuación recibe el nombre de ecuación diferencial ordinaria, si en esta ecuación existen derivadas parciales, la ecuación se denomina ecuación diferencial parcial Se denomina orden de una ecuación diferencial a la derivada en la ecuación que lo tenga mayor Se llama grado de una ecuación diferencial a la potencia a que está elevada la derivada de mayor orden Una ecuación diferencial ordinaria de primer orden es una ecuación del tipo: F (x, y, y´)=0, por ejemplo y' k y x y y xy 0 4 orden 1 grado 1 orden 3 grado 1 Se entiende por solución de una ecuación diferencial una relación entre las variables dependiente e independiente en la que no aparece ninguna derivada y que, al sustituirse en la ecuación dada, la reduce a una identidad. La solución de una ecuación diferencial ordinaria de primer orden contiene una constante arbitraria se denomina solución general En los problemas de la física e ingeniería se requieren soluciones que satisfagan determinadas condiciones. De estas condiciones se obtiene la información con la cual es posible asignar valores a las constantes arbitrarias. Este tipo de solución, que satisface estas condiciones dadas, se denomina solución particular, y las condiciones que satisface se denominan condiciones iniciales. 1 2 Así: y x 2 C es la solución general de la ecuación diferencial: y´=x. Supongamos la condición inicial y(0) =1 , entonces C = 1 , por tanto la solución particular es : y = 1 2 x 1 2 Veamos cuatro tipos principales de ecuaciones diferenciales de primer orden y primer grado. Variables separadas, Homogéneas, Lineales, Exactas 1 4.2. Ecuaciones de variables separadas Las ecuaciones diferenciales de primer orden y primer grado contienen el término elevado a la primera potencia, luego se pueden expresar en la forma dy Fx, y dx En muchos casos F(x , y ) se puede expresar como : F ( x , y ) = f(x) .g(y) . Entonces se puede poner dy dx f x g y dy g y f x dx Integrando se obtiene dy gy fxdxC Ejercicios de aplicación 1. Integrar las siguientes ecuaciones de variables separadas cos 2 x dy dx cos 2 y 1 x dy 1 y dx 2 , 2 Para la primera dy cos 2 y dx cos 2 x tang y tang x C Para la segunda 1 y 1 x dy dx 2 2 Arco Tang y =Arco Tang x +C 4.3. Ecuaciones Homogéneas Definición 1 La función M(x ,y) se dice homogénea de grado n si la suma de las potencias de x e y en cada termino de M es n : Así : M(x, y) x 2 y 3xy 2 2 y 3 es homogénea de tercer grado. 2 Si una ecuación diferencial de primer orden se puede expresar en la forma dy dx Mx , y Nx ,y Siendo M y N funciones homogéneas del mismo grado, se dice que la ecuación es homogénea. Si en la ecuación diferencial anterior siendo M y N funciones homogéneas de grado n , es posible dividirlas entre y expresar el lado derecho como una función de una sola variable v , donde se ha realizado el cambio y = v x . Por tanto se tiene dy dx vx dv Mx, y f v dx Nx, y de donde se deduce 1 dx dv f v v x que es una ecuación diferencial de variables separadas Ejercicios de aplicación 2. Integrar la ecuación diferencial: x 2 y 2 dy xy dx Cambio: y = v x dy dx vx dv v dx 1 v 2 L x Deshaciendo el cambio: L 3. Integrar la ecuación diferencial: dx 1 1 3 dv x v v 1 2v 2 L v LC 2 y x y Ce C 2y 2 dy dx xx y 3x 2 y 2 2 3y 2 Ecuación diferencial homogénea 3 x2 2 y2 1 2 Cv 1 v dv v 3 v dx 1 3v v x dv x 2 3 dx 1 3 v x 2 v 2 v 1v2 2 Deshaciendo el cambio se obtiene: 2 2 x y2 x y2 C y x 4.4. Ecuaciones diferenciales lineales Una ecuación diferencial de primer orden del tipo: y pxy qx se dice lineal, ya que tanto y’ como y aparecen en forma lineal. Para resolverla multiplicamos la ecuación anterior por e ye px dx pxye px dx El primer miembro de esta ecuación es la derivada de ye qxe p x dx px dx px dx , luego se verifica p x dx d px dx ye qx e dx La solución general será: p x dx px dx dx C yx e q x e Ejercicios de aplicación 4. Integrar la ecuación diferencial: x y 2y e x 2 ex y y x x Solución general ye 2 2 x ex x dx e x dx e C 2 x x x 1 C 4.5. Ecuaciones diferenciales exactas Una ecuación diferencial de primer orden: P( x ,y ) d x + Q( x , y) dy = 0 , es una diferencial exacta si existe una función potencial U( x , y ) , tal que 4 d U = P d x + Q dy (1) Si esta función U(x, y) existe, entonces la ecuación se convierte en d U = 0, lo cual nos conduce a la solución U (x , y ) = C .Sabemos dU U U dx dy x y al comparar con la expresión ( 1), se tiene dU U U dx dy P dx Q dy x y de donde se obtiene U U P , Q x y si suponemos que se verifica 2U 2U y x x y se obtiene , finalmente : P Q y x que es la condición para que la expresión : P( x ,y ) d x + Q( x , y) d y sea diferencial exacta . Calculo de la función potencial: La condición vista anteriormente que es el teorema de Schwarz es una condición necesaria para la existencia de función potencial. Veamos ahora que cuando se cumple esta condición es posible obtener la función potencial. En efecto: de la relación U P Ux,y Pdx C x Siendo C una constante de integración que es una función de la variable y , ya que al integrar respecto a x la y desempeña el papel de una constante . Así pues se tiene U Pdx y 5 (2) El segundo miembro de la expresión (2) no depende de x, ya que su derivada respecto de x vale cero. Luego se obtiene Φ y y Q P dx Ψy Φy Ψy dy C 1 y De donde la función potencial buscada será Ux, y Px,y dx Ψy dy C 1 Ejercicios de aplicación 5. Integrar la ecuación diferencial: 1 4xy 2y dx 1 4xy 2x dy 0 2 2 Es una diferencial exacta .Por tanto vamos a calcular la función U (x, y) = C dU U U dx dy 1 4xy 2 y 2 dx (1 4 x y 2 x 2 ) dy x y U 1 4xy 2y 2 x U 2 1 4xy 2x y Ux, y 1 4xy 2y 2 dx x 2x 2 y 2y 2 x Φy U 1 4xy 2x 2 2x 2 4xy Φ y y Φy y C 1 y La solución de la ecuación diferencial es: x 2 2x 2 y 2y 2 x y C 1 C y2 x2 y2 x dy 0 Ly dx 2x 2 xy 6. Integrar la ecuación diferencial: P x2 y2 Q y x x2 y 6 Calculo de la función potencial 2 2 U x y x y xy U y2 Ly x 2x 2 y2 y2 U 2 L y dx L y Φy 2x 2x De donde se deduce dy U x2 y2 x 1 y Φ y y Φy x x Ly C y x y xy y y2 Solución general de la ecuación diferencial: L yx 1 C 2x 4.6. Ecuaciones que se pueden transformar en exactas mediante el uso de factores de integración Sea la ecuación diferencial P(x, y) d x + Q (x, y) d y = 0 (3) y supongamos que esta ecuación diferencial no es diferencial exacta . Se llama factor de integración a una función que designamos por ( x, y) esión P( x, y ) d x +Q ( x , y ) d y = 0 (4) Sea diferencial exacta. Obligando a que la expresión (4) sea diferencial exacta se tiene que verificar ρP ρ Q y x de donde se deduce ρPy ρ y P ρ Q x ρ x Q 7 (5) En la practica la integración de esta ecuación en derivadas parciales puede ser tan difícil como la ecuación original. Luego solo podremos encontrar factores de integración en algunos casos. Veamos algunos casos particulares de interés El factor integrante depende solo de x. En este caso y 0 en la ecuación anterior de donde se obtiene ρ x Py Q x Fx ρ Q Si el lado derecho de la ecuación es función de x, se obtiene una ecuación de variables separadas, por tanto se verifica ρ Ce F x dx El factor integrante depende solo de y. En este caso x 0 en la ecuación (5), de donde se obtiene ρ y ρ Q x Py P Fy El factor integrante depende de (x, y) . La ecuación diferencial tiene un factor integrante que depende de (x, y) , ρ f ux, y En este caso se pone ρ f ux, y f(u) siendo u = u (x , y ) , de donde se obtiene f(u ) P d x + f(u) Q d y =0 (6 ) Obligando a que la ecuación (6) sea diferencial exacta, se tiene fuu y P f uPy fuu x Q f uQ x de donde se obtiene Q x Py fu f u u y P u x Q Si tiene un factor integrante que depende de u, como el primer miembro depende de u, el segundo también con lo cual se verifica 8 Q x Py fu F(u) f u u y P u x Q Ejercicios de aplicación 7. Integrar la ecuación diferencial: y 6xy dx 3xy 6x dy 0 2 2 No es diferencial exacta. Calculo del factor integrante dμ dy 1 dμ 1 uy μ dy y μ y La ecuación diferencial exacta será u y 3 6x y 2 x u u du dx dy y 3 6xy 2 dx 3xy 2 6x 2 y dy u x y 3xy 2 6x 2 y y u y 3 dx 6xy 2 dx y 3 x 3x 2 y 2 Ψy De esta expresión se tiene u 3xy 2 6x 2 y 3xy 2 6x 2 y Ψ y y Ψy C1 y La integral general será: C 1 C y 3 x 3x 2 y 2 4.7. Ecuación diferencial de Bernouilli La ecuación diferencial de Bernouilli, es una ecuación del tipo y A(x)y B(x)y m 0 , Para resolverla dividimos por y m , con lo cual se tiene y 1 Ax m 1 Bx 0 m y y 9 R Realizamos el cambio u 1 y , a continuación derivamos respecto de x, con lo cual se tiene m 1 1 u Ax u Bx 0 m1 que es una ecuación diferencial lineal . Finalmente se deshace el cambio se obtiene la solución general de la ecuación primitiva Ejercicios de aplicación 8. Resolver la ecuación diferencial: xy y 2 dx dy 0 3 Esta ecuación diferencial se puede poner en la forma y 2x x0 y4 y3 Cambio 1 u , con lo cual se obtiene: y3 2 1 u C e 3x 2 Deshaciendo el cambio, se obtiene: 2 1 1 C e 3x 3 2 y 4.8. Ecuaciones de primer orden no lineales en y’ 4.8.1. Ecuación de Lagrange. Es una ecuación de la forma y x f y Φy Derivando respecto a x, y haciendo y’ = p, se verifica y f y xf y y dy dy dp dp Φ y y p f p x fp p Φ p p dx dx dx dx Pongamos ahora 10 p dp 1 1 dx dx x p dp De donde se obtiene p f p x fp p 1 1 Φ p p , xp xp que da lugar a la ecuación lineal x p, fp p p f p x Φ p p pf p de esta ecuación se obtiene una solución de la forma : x C p . La solución general de la ecuación diferencial en forma paramétrica será x ΨCp y ΨCpf p Φp Caso particular: Si : p - f(p) = 0 , siendo p0 una raíz de esta ecuación , estando (p0) definida , se puede comprobar que : y p 0 x Φp 0 satisface la ecuación diferencial .Si esta solución no se obtiene de la solución general para un valor particular de C , se dice entonces que es una solución singular . Ejercicios de aplicación 9. Resolver la ecuación diferencial: y 2 x e y y 0 Ecuación de Lagrange, para resolverla hacemos y´= p, a continuación derivamos respecto a x, por tanto se tiene y xp 2 e p p 2 p p 2 2xp dp dp dp 1 1 1 p2 ep 2pe p p 2 2xp p 2 e p 2p e p dx dx dx xp xp xp se obtiene la ecuación lineal 11 x p e p p 2 2x p1 1p Las ecuaciones paramétricas del haz integral son 1 x C e p p 2 p 1 2 p 1 2 y p Ce p p 2 p 1 2 p 1 4.9. Ecuación diferencial de Clayrunt Es un caso particular de la ecuación de Lagrange cuando f(y´) = y´ , se tiene: y x y' Φ(y) . Para resolverla aplicamos el método anterior 0 p x Φp pp p x Φp p p 0 y C La integral general es: y= C x+ (C) Por otra parte de x Φ p p 0 x Φ p p , en este segundo caso la solución es y p Φ p p Φp x Φ p p Estas ecuaciones son las ecuaciones paramétricas de una integral de la ecuación de Clayrunt . Si se puede eliminar el parámetro p , se obtiene una ecuación de la forma f ( x , y )= 0 Esta curva integral se lla ma solución singular de la ecuación de Clayrunt . La envolvente de la familia: y = C x +(C) , se obtiene eliminando C en el sistema y Cx ΦC 0 x ΦC y es la curva envolvente de la familia de rectas dadas por la integral general . Luego podemos decir que a toda ecuación de Clayrunt corresponde siempre una integral general y una integral singular , obteniéndose la primera al reemplazar la derivada de la función por una constante arbitraria y resultando la segunda de la eliminación de la constante entre dicha integral general y su derivada respecto a la constante , la integral general representa la tangente a una curva , la solución singular da la envolvente de aquellas rectas tangentes . 12 Ejercicios de aplicación 10. Integrar la ecuación diferencial: y xy y 2 1 La integral general se obtiene haciendo y ´= C, por tanto la integral general es y CxC 2 1 La integral singular se obtiene calculando la envolvente de la integral general y CxC 2 1 x2 y 1 4 0 x 2 C 4.10. Trayectorias ortogonales Sea el haz de curvas: F( x , y , c ) =0 , de ecuación diferencial : ( ) .Se llama trayectoria de un haz de curvas , a una curva que corta a todas las del haz bajo un mismo ángulo .Se trata de hallar las trayectorias de ángulo , ya que la tangente a la curva y la tangente a la trayectoria forman un ángulo Fig.1 Sea tg y tg los coeficientes angulares de la curva del haz y de la trayectoria asociada respectivamente, en el punto (x, y). Se tiene entonces y tgα tg β v 13 tgβ tg v 1 tgβ tg v Por tanto, si f(x, y, y´)=0 es la ecuación diferencial del haz dado, la de sus trayectorias isogonales de ángulo v, será f(x, y, Si se trata de trayectorias ortogonales v y y tgv )0 1 ytg v π π , es decir , αβ , la relación entre y´ e y 1 resulta ser : 2 2 1 y 1 Por tanto, la ecuación diferencial de las trayectorias ortogonales será: 1 f x,y, 0 y 4.11. Trayectorias ortogonales de ángulo en coordenadas polares Si la ecuación diferencial de la familia de curvas es f ρ ,θ,ρ 0 , la ecuación diferencial de la familia de curvas ortogonales vendrá dada por la ecuación ρ2 f ρ , θ, ρ 0 Ejercicios de aplicación 11. Hallar las trayectorias ortogonales del haz de curvas: y m =C x n ym C xn Ecuación diferencial del haz de curvas: my Dividiendo por x n 1 m 1 yx n y n nx n 1 0 e y m 1 , haciendo y 1 , e integrando se obtiene y n ydy m xdx n y 2 mx 2 C 1 Que son cónicas con ejes los de coordenadas n ydy m xdx n y 2 mx 2 C 1 14 12. Trayectorias ortogonales del haz de cardioides: =C (1+cos θ) ρ C 1cosθ Ecuación diferencial del haz de cardiodes: ρ1 cosθ ρsenθ 0 Ecuación diferencial del haz de trayectorias ortogonales ρ2 1 cosθ ρ senθ 0 ρ El haz de curvas será: ρ dρ 1 cosθ dθ ρ senθ C θ 2 cos 2 Ejercicios resueltos 1. Integrar la ecuación diferencial: 3y y ay x 1 2 3 Cambio: y3 = Y 3y 2 y Y Ya Yx 1 Yx e a dx a x a x x 1e adx C e ax e x 1 e C a2 a La solución general será y 3 Ce a x 2.Integrar la ecuación diferencial: y ax a 1 a2 2 y 1 , calculando la solución particular que pasa por el x punto P ( 1, -1) 15 yx e 2 x 2 1 1 dx dx 1e x C x 2 2 dxC x 2 C x x Solución particular: y = x -2 x2 3. Integrar la ecuación xy 2 y 3 dx 1 xy 2 dy 0 , calculando previamente un factor integrante dependiente de y Calculo del factor integrante ρ y 2 1 ρ 2 ρ y y 1 x dy 0 , de donde se obtiene 2 y La ecuación diferencial exacta será x y dx U x y x x2 U xy Φy U 1 2 x y y2 1 1 x xΦ y y Φy 2 y y x2 1 Integral general: x y C 2 y 4. Resolver la ecuación diferencial x y y dx x dy 0 , sabiendo que admite un factor integrante 2 2 3 que depende del producto (x. y) Sea: ρ=f (u), siendo u = x .y. Calculo del factor integrante 3x 2 x 2 2 y fu 2 2 3 2 3 f u x yxy x y xy u f u 1 1 2 2 2 u x y La nueva ecuación diferencial será 16 1 1 2 y x Integral general: x dx 2 dy 0 y 1 x C x y 5. Resolver la ecuación diferencial: y y 1 3 x 1 y 2 x1 2 Ecuación de Bernouilli y 1 1 3 x 1 0 2 y y(x 1 2 Cambio 1 u . La ecuación diferencial dada se transforma en la ecuación lineal y u u 1 3 x 1 x 1 2 Solución general de la ecuación lineal: u 1 x 14 Cx 1 6 Solución general de la ecuación diferencial: 1 x 1 Cx 1 y 6 4 7. Integrar la ecuación diferencial: y 2xy 2x y 3 3 Ecuación de Bernouilli y 2x 2 2x 3 3 y y Cambio u 1 . La ecuación dada se transforma en la ecuación lineal y2 u4xu 4x 3 Solución general de la ecuación lineal 17 2 1 u x 2 Ce 2 x 2 Solución general de la ecuación diferencial dada: 2 1 1 x 2 Ce 2 x 2 2 y 8. Integrar la ecuación diferencial: 2xyy 3x y 1 4 2 2xy dy 3x 4 y 2 1 dx 3x y 2 1 dx 2xydy 0 4 No es diferencial exacta. Calculo del factor integrante ρ x 2 y2 y 2 1 ρ 2 ρ 2 x y x x 1 y2 2y La ecuación exacta será: 3x 2 2 2 dx dy 0 x x x y2 1 x3 C Integral general: x x 9. Integrar la ecuación diferencial: xy x y x y 1 y 0 2 2 2 La ecuación diferencial adopta la forma: xy 2 dx x 2 1 y 1dy y 1 xdx dy 2 1 y2 x Integral general x2 1 1 L C y y 10. Integrar la ecuación diferencial: dy 1 y b 0 dx 2 a x y 18 La ecuación diferencial es: y 2 2ba x dx2 2 a xy dy 0 No es diferencial exacta .Busquemos un factor integrante dependiente de x ρ x 2 1 ρ ρ ax ax2 Ecuación diferencial exacta y2 2y 2b a x 2 a x dx a x dy 0 y2 2bLa x C Integral general: a x 11. Integrar la ecuación diferencial: x x 1y 2x y x 1 0 2 y Ecuación diferencial lineal: y e Integral general y 2 x 1 2 y 2 x 1 x x 1 2 dx x 1 x 1 x2dx1 e dx C 2 x x 1 1 x C x x 1 1 2 12. Integrar la ecuación diferencial x y 4y 2x 4 0 , determinando la solución particular que pasa 2 por el punto ( 1 , 1) 4 x Ecuación diferencial lineal: y y 2x 4 x 4 4 4 x dx x dx Integral general: y e C C x 4 x 2 1 2x e x Integral particular: y x 4 x 2 1 13. Integrar la ecuación diferencial: 3xy 2 dx 2x ydy 0 2 2 19 No es diferencial exacta .Busquemos un factor integrante que depende solo de x ρ x 1 ρ x ρ x La ecuación diferencial exacta será: 3x 2 y 2 2x dx2x 3 ydy 0 Integral general: x 3 y 2 x 2 C 14. Integrar la ecuación diferencial: x y 2 xy dy y dx 0 Hagamos el cambio: x= v y d x= v dy + y d v v y y 2 v y 2 dy yv dy y dv Simplificando se tiene dv 1v ye 2 1 v dy y e c1 Deshaciendo el cambio ye 15. Integrar la ecuación diferencial: y' 2 yx y C y x3 0 x Ecuación diferencial lineal ye dx x dx x 3 x e C C x4 y x 5 20 16. Integrar la ecuación diferencial: x y' y y L x 0 2 Ecuación diferencial de Bernouilli y' y y 2 Lx x y' Lx 1 2 yx x y Cambio: y' 1 u 2 u' y y Se llega a la ecuación diferencial lineal u' ux C x L x 1 y(x) Lx 1 u x x 1 Cx Lx 1 1 17. Integrar la ecuación diferencial: y' x y 2 0 Ecuación diferencial de variables separadas dy dy x y x dx dx y x2 y C 4 18. Integrar la ecuación diferencial: 2 y 2 x y'Log y' Ecuación diferencial de Lagrange: y’= p, se llega a la ecuación diferencial lineal x 'p 2 x 1 1 2 p p 21 C 1 x p 2 p y 2 C 2 Log p p 19. Integrar la ecuación diferencial: y x y' y'3 3 Ecuación diferencial de Clayrunt Solución general: y C x Integral singular: y 1 3 C 3 3 2 2 x 3 20. Integrar la ecuación diferencial: y x y'1 - log y' Solución general: y C x 1 log C Integral singular: y 2 log x 21. Integrar la ecuación diferencial: x y'y e y' Solución general: y C x e C Integral singular: y x log x x 22. Integrar la ecuación diferencial: (2 x-y2) d x+2 x y dy =0 mediante un factor integrante Busquemos un factor integrante que depende de x ρ'x 2 1 ρ 2 ρ x x 2 y2 La ecuación diferencial 2 x x 2y dx dy 0 es exacta x Integral general 22 y2 2Lx C x 23 24 25