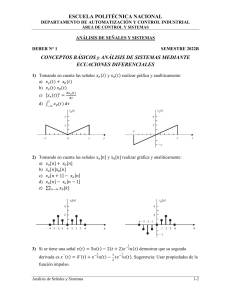
Isi1.pdf
Anuncio
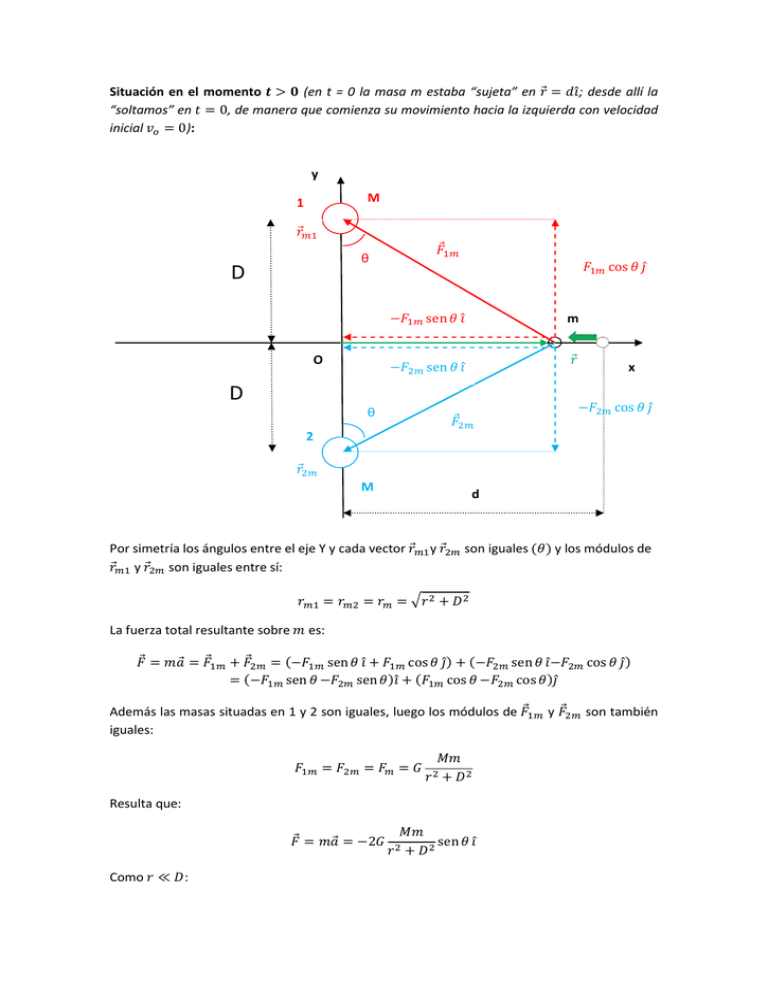
Situación en el momento (en t = 0 la masa m estaba “sujeta” en ; desde allí la “soltamos” en , de manera que comienza su movimiento hacia la izquierda con velocidad inicial ): y M 1 θ D m O x D θ 2 M Por simetría los ángulos entre el eje Y y cada vector y son iguales entre sí: La fuerza total resultante sobre d y son iguales es: Además las masas situadas en 1 y 2 son iguales, luego los módulos de iguales: Resulta que: Como : y los módulos de y son también y Por tanto podemos poner: Y Luego queda: Además: Por lo que: Llamando: Tenemos: Como (ya que el orden de magnitudes lo permite: por ejemplo, haciendo y , resulta que ), podemos considerar: Que es la ecuación diferencial, correspondiente a un m.a.s., que hay que resolver. De aquí: Las condiciones iniciales son: Luego: Y Eligiendo , queda: Luego el período es: La velocidad será: Y la aceleración: Excursión 1 - ¿Qué pasaría … …si utilizamos: Obtenemos: m Excursión 2 – Y ¿si no simplificamos? La ecuación diferencial que define el movimiento, sin despreciar ningún elemento, quedaría de esta manera: Mi amigo Wolfram dice que no sabe resolver esta ecuación diferencial, así que lo más sensato parece ser simplificar como hemos hecho arriba.