b f(b) a B f(a)A b - a f(a) A a

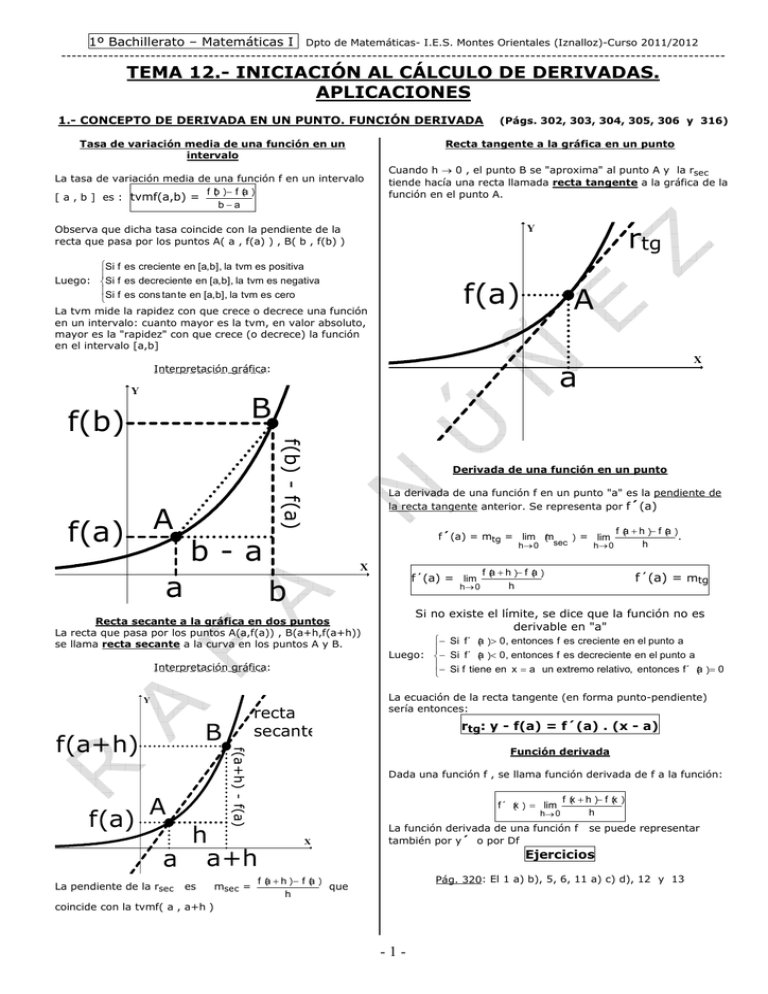
1º Bachillerato – Matemáticas I Dpto de Matemáticas- I.E.S. Montes Orientales (Iznalloz)-Curso 2011/2012
------------------------------------------------------------------------------------------------------------------------------
TEMA 12.- INICIACIÓN AL CÁLCULO DE DERIVADAS.
APLICACIONES
1.- CONCEPTO DE DERIVADA EN UN PUNTO. FUNCIÓN DERIVADA
(Págs. 302, 303, 304, 305, 306 y 316)
Recta tangente a la gráfica en un punto
Tasa de variación media de una función en un
intervalo
a
f a
b b
f
La tasa de variación media de una función f en un intervalo
()(
− )
[ a , b ] es : tvmf(a,b) =
−
Cuando h → 0 , el punto B se "aproxima" al punto A y la rsec
tiende hacía una recta llamada recta tangente a la gráfica de la
función en el punto A.
Y
Observa que dicha tasa coincide con la pendiente de la
recta que pasa por los puntos A( a , f(a) ) , B( b , f(b) )
a
v
i
t
a a
v
g
i
t
e
i
s n
o s
p e
s
m
e v
t
a
l
,
]
b
,
a
[
n
e
e
t
n
e
i
c
e
r
c
e
d
s
e
f
i
S
m
v
t
a
l
,
]
b
,
a
[
n
e
e
t
n
e
i
c
e
r
c
s
e
f
i
S
rtg
o
r
e
c
s
e
m
v
t
a
l
,
]
b
,
a
[
n
e
e
t
n
a
t
s
n
o
c
s
e
f
i
S


Luego: 


La tvm mide la rapidez con que crece o decrece una función
en un intervalo: cuanto mayor es la tvm, en valor absoluto,
mayor es la "rapidez" con que crece (o decrece) la función
en el intervalo [a,b]
f(a)
A
Interpretación gráfica:
Y
a
B
f(b)
f(b) - f(a)
Derivada de una función en un punto
La derivada de una función f en un punto "a" es la pendiente de
la recta tangente anterior. Se representa por f´(a)
a
f
hh
a
f
0
m
i
l
h
c
e
s
a
o
t
n
u
p
l
e
n
e
e
t
n
e
i
c
e
r
c
e
d
s
e
f
s
e
c
n
o
t
n
e
,
0
( ) =
rtg: y - f(a) = f´(a) . (x - a)
+) (
− )
→
La función derivada de una función f
también por y´ o por Df
X
x
f
(
hh
x
f
0
m
i
l
h
( ) =
se puede representar
Ejercicios
+) (
− )
Pág. 320: El 1 a) b), 5, 6, 11 a) c) d), 12 y 13
que
coincide con la tvmf( a , a+h )
-1-
0
a
´
f
s
e
c
n
o
t
n
e
,
o
v
i
t
a
l
e
r
o
m
e
r
t
x
e
n
u
a
=
x
´
f
(
msec =
( ) >
( ) <
a
f
es
−

Luego: −
−

Dada una función f , se llama función derivada de f a la función:
h h
La pendiente de la rsec
Si no existe el límite, se dice que la función no es
derivable en "a"
Función derivada
a
f
h
a a+h
f´(a) = mtg
→
a
o
t
n
u
p
l
e
n
e
e
t
n
e
i
c
e
r
c
s
e
f
s
e
c
n
o
t
n
e
,
0
A
+) (
− )
x
n
e
e
n
e
i
t
f
i
S
recta
secante
f(a+h) - f(a)
f(a+h)
.
La ecuación de la recta tangente (en forma punto-pendiente)
sería entonces:
Y
B
→
a
´
f
i
S
Interpretación gráfica:
+) (
− )
a
´
f
i
S
Recta secante a la gráfica en dos puntos
La recta que pasa por los puntos A(a,f(a)) , B(a+h,f(a+h))
se llama recta secante a la curva en los puntos A y B.
m
b
(
(
) =
a
f
f´(a) =
→
hh
a
X
a
f
0
m
i
l
h
b-a
(
0
f´(a) = mtg =
m
i
l
h
f(a) A
f(a)
X
1º Bachillerato – Matemáticas I Dpto de Matemáticas- I.E.S. Montes Orientales (Iznalloz)-Curso 2011/2012
-----------------------------------------------------------------------------------------------------------------------------2.- CÁLCULO DE DERIVADAS
(Págs. 307, 308, 309 y 316)
DERIVADAS FUNDAMENTALES
REGLAS DE DERIVACIÓN
y=x
y´ = 0
Ejemplo: y = 7 → y´ = 0
→ y´ = k x
, k∈R
Ejemplos:
1) y =x
7
→
y´= 7x
6
y´ = 1
Ejemplo:
5
3
2
5
3
2
4
y=x
2
= 5x + 3x - 2x
----------------------------------------------------------
2
→
y´ = 2x
(a.u)´ = a . u´ , donde a ∈ R
6
6
5
Ejemplo: (4x )´ = 4 .(x )´ = 4.(6x )= 24x
1
CASOS
1 2
x
→
−
y´ =
5
Como consecuencia:
(a u ± b v)´ = a . u´ ± b. v´, donde a , b ∈ R
Ejemplo:
2
x
2
x
→ y´ =
2
(3x + 5x - 4)´ = 3.(x )´+ 5. x´ - (4)´ = 6x+5 - 0
1
x
y=
5
3
x
3
5
3
−
=
−
2
1
23
53
−
=
−
−
y´=
23
→
=
x
23
x
x
2
x
23
−
3
y´=
−
23
1
3) y =
−
derivables. Se pueden usar las siguientes reglas:
(x + x - x )´ = (x )´ + (x )´ - (x )´ =
y=
--------------------------------------------
→
y=x
1 x
4 5
x
1 5
x
−
=
1
4
− −
y´= −
→
4
= −
x
4
x
−
=
5
y´= −
4
2) y =
1 4
x x
4
-------------------------------------------−
son
y
(u ± v)´ = u´± v´
Función potencia
k
k-1
PARTICULARES
y=c →
Entonces las funciones: u ± v , a.u , u.v
u v
Sean u y v dos funciones derivables.
Función constante
La derivada de la función constante vale 0
-----------------------------------------------------------
Función exponencial
x
→ y´ = a . ln(a)
x
x
→
y´ = 2 . ln(2)
2
= 2x ln x + x .
´
− ( )
2
x
(
=
1
x 2
x
.
e
x
=
x
.
x
e
x
.
´
x
−
=
)
1
.
e
CASO
v
 (
 =


x

Ejemplo: 


2
y´ =
´
v
u
→
−
=
e
y = ln(x)
´



v
´
u



´
( )
2
= 2x ln x + x
2
x
(x) → y´ =
x
x
.
e
2
y´ = e
x
y = log
2
1 n
l
.
x
Ejemplo:
→
x x
e
( )
a
x
uv
y = log (x) → y´ =
y=e
1 x
a
n
1 l
.
x
Función logarítmica
2
---------------------------------------------------------PARITUCL
AR
Ejemplo: y = 2
2
Ejemplo: (x .ln x)´ = (x )´.ln x + x .(ln x)´ =
1 x
y=a
x
CASO
PARITUCLAR
(u.v)´ = u´ . v + u . v´
−)
DERIVADA DE LA FUNCIÓN COMPUESTA (REGLA DE LA CADENA)
Sean u y f dos funciones. La derivada de la función compuesta f o u se obtiene usando:
=
1
x 2
x
−
1
x 2
2 x
−
2
2x =
1
. u´ =
u´ representa a u´(x) ]
2
y´ =
u
→
2
[ u(x) = x - 1 , u´(x) = 2x ] ; y =
y
1 2
x
[ donde u representa a u(x)
2
1
−
1
x
2
Ejemplo: y =
y´ = f´(u) . u´
u
→
y = f(u)
−
DERIVADA DE UNA FUNCIÓN ELEVADA A OTRA FUNCIÓN
Sea la función f(x) = u(x)
ln [ f(x) ] = ln [u(x)
v(x)
]
v(x)
. Para calcular su derivada, tomamos logaritmos en los dos miembros, después derivamos ambos
miembros y, por último, despejamos f´(x)
→ ln [ f(x) ] = v(x) . ln [u(x)] . Después se deriva en los dos miembros y se despeja f´(x)
Lo haremos en los ejercicios en clase.
Ejercicios
Polinómicas y constantes: Pág. 320: 15, 17, 21 y 34a)
Con radicales: Pág. 308: 2 y 4
Pág. 325: 3 a)
Producto de funciones: Pág. 308: 7, 8 y 9
Racionales: Pág. 308: 10 y 11
Pág. 320: 18
Cociente (no racionales): Pág. 308: 12
Regla de la cadena: Pág. 309: 14, 18 y 19
Pág. 321: 25 y 27 a)
Pág. 309: 16
Pág. 320: 20
Pág. 321: 22, 24, 26, 27 b), 28 a), 29, 32 a), 33, 34 b) y 35 b)
Pág. 323: 71 (salvo el e))
2
2x+5
Función elevada a otra función: Deriva las funciones: a) y = (3x - x + 1)
-2-
3x-1
b) y = x
1º Bachillerato – Matemáticas I Dpto de Matemáticas- I.E.S. Montes Orientales (Iznalloz)-Curso 2011/2012
-----------------------------------------------------------------------------------------------------------------------------3.- APLICACIONES DE LAS DERIVADAS (Págs. 310, 312, 313, 314, 315, 317, 318 y 319)
Observa su gráfica.
Calculo de la ecuación de la recta tangente a la
gráfica en un punto
Y
Dada una función f , la ecuación de la recta tangente a la
gráfica de f en el punto A ( a , f(a) ) vimos que era:
X
rtg: y - f(a) = f´(a) . (x - a)
Estudio de la curvatura y los puntos de inflexión de una
función
Estudiar la curvatura de una función es averiguar los intervalos
Si pasamos f(a) al segundo miembro
rtg: y = f(a)
+
f´(a) . (x - a)
Para poder calcular dicha ecuación es necesario que existan
tanto f(a) como f´(a).
Después sustituimos en la fórmula los valores:
" a " , " f(a) "
y
" f´(a) "
Estudio de la monotonía de una función
Estudiar la monotonía de una función consiste en averiguar
los intervalos donde es creciente, decreciente o constante
f´´(x) = [ f´(x) ]´
o
l
a
v
r
e
t
n
i
n
u
n
e
x
´
´
f
o
l
a
v
r
e
t
n
i
o
h
c
i
d
n
e
,
0
o
l
a
v
r
e
t
n
i
n
u
n
e
x
´
´
f
o
l
a
v
r
e
t
n
i
o
h
c
i
d
n
e
,
0
Usaremos que:
(




(




(

)
∪
e
d
a
m
r
o
f
)
∩
↔ ( ) <
) ↔( ) =
o
l
a
v
r
e
t
n
i
o
h
c
i
d
n
e
,
0
Para estudiar la monotonía de una función f tendremos que
estudiar el signo de la función derivada.
↔ ( ) >
x
´
´
f
a
x
e
v
n
o
c
i
n
,
a
v
a
c
n
ó
c
i
n
o
l
a
v
r
e
t
n
i
o
h
c
i
d
n
e
,
0
x
´
f
o
l
a
v
r
e
t
n
i
n
u
n
e
e
t
n
a
t
s
n
o
c
f
↔( ) =
Para estudiar la curvatura y los puntos de inflexión de una
función procederemos de igual forma que en el estudio de la
monotonía y extremos relativos pero usando, en vez de la
primera derivada, f´(x), la derivada segunda, f´´(x).
o
l
a
v
r
e
t
n
i
n
u
n
e
a
t
c
e
r
a
n
u
a
c
i
f
á
r
g
r
o
p
e
n
e
i
t
f
o
l
a
v
r
e
t
n
i
o
h
c
i
d
n
e
e
t
n
e
i
c
e
r
c
e
d
s
e
f
s
e
c
n
o
t
n
e
,
o
l
a
v
r
e
t
n
i
n
u
n
e
0
x
´
f
i
S
( ) <
Los puntos de inflexión son puntos donde la función es
continua y pasa de ser convexa a ser cóncava o al revés.
a
v
a
c
n
ó
c
f
( ) >
o
l
a
v
r
e
t
n
i
o
h
c
i
d
n
e
e
t
n
e
i
c
e
r
c
s
e
f
s
e
c
n
o
t
n
e
,
o
l
a
v
r
e
t
n
i
n
u
n
e
0
x
´
f
i
S








⋂).
e
d
a
m
r
o
f
a
x
e
v
n
o
c
f
Como la derivada representa la pendiente de la recta
tangente, podemos deducir que:
donde es convexa (forma de U) ó cóncava (forma de
Representación gráfica de funciones
Para ello, resolvemos la ecuación f´(x) = 0 . Sus
soluciones se suelen llamar puntos singulares
Para representar gráficamente una función es conveniente
analizar:
1) El dominio de definición
Después representamos sobre la recta real los puntos
singulares y los puntos de discontinuidad de f.
2) La continuidad y las asíntotas verticales (posición de la gráfica
respecto de las asíntotas)
3) Las asíntotas horizontales y oblicuas (posición de la gráfica
respecto de las asíntotas)
De esta forma se determinan los intervalos donde la
derivada es positiva, negativa o nula y por tanto los
intervalos donde es creciente, decreciente o constante.
4) La monotonía y los extremos relativos.
Estudio de los extremos relativos de una función
5) La curvatura y los puntos de inflexión
Los extremos relativos de una función son los máximos o
mínimos relativos.
Si además, calculamos los puntos de corte con los ejes de
coordenadas tendremos más elementos para su representación.
Recuerda que los extremos relativos son puntos donde la
función es continua y pasa de ser creciente a ser
decreciente o al revés.
Si detectamos que la función es simétrica respecto del eje Y
(esto ocurre cuando f(-x) = f(x) ) o simétrica respecto del origen
de coordenadas ( esto ocurre cuando f(-x) = - f(x) ) entonces
sólo es necesario estudiarla para x > 0 y luego, por simetría,
deducir la gráfica para x < 0.
Por tanto, al estudiar la monotonía se pueden deducir
cuáles son los extremos relativos.
Ejercicios
También se pueden determinar los extremos relativos
hallando las soluciones de la ecuación f´(x) = 0 y después
averiguando cuál de las soluciones corresponde a un
máximo, mínimo o ninguno de los dos.
Recta tangente: Pág. 321: 44, 45, 46 y 47
Pág. 323: 63, 64, 66, 67, 68 y 69
Monotonía y extremos: Pág. 322: 52, 53 y 54
Ojo que el que sea f´(a) = 0 no asegura que en x = a haya
un extremo relativo.
3
Por ejemplo, para la función f(x) = x
→
f´(x) = 3x
2
Representación gráfica:
2
f´(0) = 3.0 = 0 , pero en x = 0 no hay ningún extremo
Págs. 323 y 324: 72 a) e) g) h), 73, 74 y 75 a) c) f) h) i) j)
3
relativo: la función y = x es siempre creciente.
-3-