ALGEBRA LINEAL CON EL USO DE MATLAB AUTORES Omar Saldarriaga

ÁLGEBRA LINEAL
CON EL USO DE MATLAB
AUTORES
Omar Saldarriaga
Ph.D., State University of New York at Binghamton
Profesor Asociado
Instituto de Matemáticas
Universidad de Antioquia
Hernán Giraldo
Ph.D., Universidad de São Paulo
Profesor Asociado
Instituto de Matemáticas
Universidad de Antioquia
ii
c Copyright by Omar Saldarriaga, 2010.
All rights reserved.
Índice general
1. Álgebra de matrices
1.1. Sistemas de Ecuaciones Lineales
3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2. Operaciones con Matrices y Vectores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
1.3. Inversa de una Matriz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
1.4. Matrices Elementales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
1.5. Inversas Laterales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
2. Espacios Vectoriales
45
2.1. Definición y Ejemplos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
2.2. Subespacios
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
2.3. Independencia Lineal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
2.4. Conjuntos generadores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
2.5. Bases
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
2.6. Subespacio generado por un conjunto de vectores . . . . . . . . . . . . . . . . . . . . . . . . . . .
69
2.7. Subespacios fundamentales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
2.8. Subespacio generado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
2.9. El Teorema de la base incompleta en Rm
81
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3. Transformaciones Lineales
85
3.1. Definición y Ejemplos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85
3.2. Transformaciones Lineales Inyectivas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
3.3. Transformaciones Lineales Sobreyectivas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
3.4. Isomorfismos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
96
3.5. Espacios Vectoriales Arbitrarios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
3.5.1. Transformaciones lineales entre espacios vectoriales arbitrarios. . . . . . . . . . . . . . . . 103
3.6. Propiedades de los Espacios Vectoriales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
3.7. Suma Directa de Espacios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
iii
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
4. Ortogonalidad en Rn
1
119
4.1. Producto interno en Rn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
4.2. Proyección Ortogonal sobre un Vector . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
4.2.1. La matriz proyección. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
4.3. Proyección Ortogonal sobre un Subespacio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
4.4. Mı́nimos Cuadrados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
4.5. El Proceso Gramm-Schmidt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
4.6. La Factorización QR de una Matriz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 152
5. Determinantes
157
5.1. Definición y ejemplos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
5.2. Determinantes y operaciones elementales de fila . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164
5.3. Propiedades del determinante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172
5.4. Matriz Adjunta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
5.5. La Regla de Cramer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177
5.6. Interpretación Geométrica del Determinante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179
6. Valores y Vectores Propios
187
6.1. Polinomio Caracterı́stico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 187
6.2. Matrices Similares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 198
6.3. Cambio de Base . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
6.3.1. La matriz de una transformacion con respecto a dos bases . . . . . . . . . . . . . . . . . . 207
6.4. Diagonalización . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213
6.5. Matrices Simétricas y Diagonalización Ortogonal . . . . . . . . . . . . . . . . . . . . . . . . . . . 217
6.6. Formas Cuadráticas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219
6.7. Ejercicios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 222
7. Aplicaciones
7.1. Potencia de una matriz
225
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225
7.1.1. Relaciones de recurrencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 226
7.1.2. Cadenas de Markov . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 227
7.2. Exponencial de una matriz diagonalizable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228
7.2.1. Sistemas Lineales de Ecuaciones diferenciales . . . . . . . . . . . . . . . . . . . . . . . . . 229
2
Capı́tulo 1
Álgebra de matrices
En este capı́tulo veremos ... Las letras m,n, i, j y k denotarán números enteros positivos y denotaremos por
R el conjunto de los números reales ... mı́n{m, n} es el menor número entre m y n... el conjunto de matrices de
tamanõ m × n será denotado por Mmn (R) y por Mn (R) cuando m = n. El conjunto vacı́o ??
1.1.
Sistemas de Ecuaciones Lineales
Comenzamos esta sección ilustrando un ejemplo del tema central del capı́tulo, el cual es la solución de
sistemas de ecuaciones lineales, y usaremos este ejemplo para introducir el método de solución conocido como
reducción Gauss-Jordan en matrices.
Consideremos el siguiente sistema de dos ecuaciones en dos incógnitas:
x + 3y = 4
(1.1)
4x + 6y = 10
(1.2)
Existen varios métodos para resolver este sistema, por la similitud con el método que expondremos en esta
sección destacamos el de eliminación.
Este método usa dos operaciones básicas para llevar a la solución de un sistema lineal las cuales son:
1. Sumar un múltiplo de una ecuación a otra ecuación con el objetivo de eliminar una de las variables, por
ejemplo la operación
-4 Ecuación(1.1) + Ecuación(1.2)
elimina la variable x y produce la ecuación −6y = −6.
2. Multiplicar una ecuación por una constante no cero con el objetivo de simplicarla, por ejemplo si multiplicamos la nueva ecuación −6y = −6 por − 16 obtenemos y = 1.
3
4
3. Si multiplicamos esta última ecuación (y = 1) por -3 y se la sumamos a la Ecuación (1.1), obtenemos
x = 1. Finalmente la solución al sistema está dada por los valores: x = 1 y y = 1.
Los métodos que veremos en este libro son:
1. El método de reducción Gauss-Jordan, el cual veremos en esta sección.
2. El método de multiplicación por la matriz inversa, este método solo funciona en algunos casos, ver Teorema
1.12 en la Sección 1.3.
3. El método de multiplicación por la inversa a la izquierda de la matriz, este método solo funciona en algunos
casos, ver Sección 1.5
4. La regla de Cramer, ver Sección 5.5.
Retomando las soluciones para un sistema, vale la pena notar que si tenemos un sistema de dos ecuaciones
lineales en dos incógnitas, hay tres posibles respuestas y estas son:
1. El sistema tiene solucion única (como en el ejemplo ilustrado anteriormente).
2. El sistema no tiene solución (o solución vacı́a), caso en el cual, decimos que es inconsistente.
3. El sistema tiene infinitas soluciones, caso en el cual decimos que el sistema es redundante.
Cuando se tiene una ecuación lineal en dos variables, esta representa una lı́nea recta en el plano, las tres
posibles soluciones descritas corresponden a las diferentes posibilidades geométricas las cuales son: las rectas se
intersectan (solución única), las rectas son paralelas (solución vacı́a) o las rectas coinciden (infinitas soluciones).
Estas se ilustran en la Figura 1.1.
Cuando tratamos de resolver un sistema 3×3, de tres ecuaciones en tres incógnitas, también podemos obtener,
al igual que en el caso anterior (caso 2×2), tres posibles respuestas: solución única, solución vacı́a o infinitas
soluciones. En este caso, una ecuación en tres variables representa un plano en el espacio, las posibilidades
geométricas se muestran en las Figuras 1.1 y 1.1. Sin embargo, a diferencia del caso 2×2, la solución vacı́a no
se obtiene exclusivamente en el caso de que los planos sean paralelos como se observa en la Figura 1.1. También
se puede ver en la Figura 1.1 que hay diferentes casos que conducen a infinitas soluciones y no solo cuando los
planos coinciden.
Uno de los objetivos de la sección es mostrar que aún en dimensiones mayores se presentan exactamente las
mismas tres posibilidades. El caso general lo resolveremos usando matrices, asociaremos a cada sistema lineal
una de estas y aplicaremos operaciones elementales de fila para resolver el sistema. Las operaciones elementales
de fila sobre matrices son simplemente operaciones equivalentes a las mencionadas en el método de eliminación
al principio de la sección.
5
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Definición 1.1. Una matriz real es un arreglo rectangular de números reales en m filas y n columnas


a11 · · · a1n


.. 
 ..
..
;
 .
.
. 


am1 · · · amn
donde aij es un número real para i = 1, . . . , m y j = 1, . . . , n. A esta matriz se le llama una matriz de tamaño
m × n.
En esta sección se esta interesado en operaciondes de fila de una matriz, ası́ en esta sección se donotará la
i-ésima fila de una matriz A por Fi . Además, de ahora en adelante el conjunto de matrices de tamanõ m × n
será denotado por Mmn (R) y por Mn (R) cuando m = n.


1 −1
 es una matriz de tamaño 2×2. Esta matriz la definimos en MatLab
Ejemplo 1.1. (MatLab) A = 
2
0
de la siguiente forma:
>> A = [1, −1; 2, 0]
y MatLab guardarı́a la matriz como el arreglo rectangular
A=
1
−1
2
0
En general, para definir matrices en MatLab se escriben las entradas entre corchetes, escribiendo las entradas
de las filas separadas con coma y separando las filas con punto y coma.
A un sistema lineal de m ecuaciones con n incognitas,
a11 x1 + · · · + a1n xn = b1
..
.
am1 x1 + · · · + amn xn = bm ,
se le asocia la matriz de tamaño m × (n + 1)

a11

 ..
 .

amn
···
..
.
a1n
..
.
···
a1n

b1

.. 
. 

bm
llamada la matriz de coeficientes o matriz asociada. Cada fila de esta matriz tiene los coeficientes de cada
una de las ecuaciones incluyendo el término constante al final de la misma y cada columna está asociada a una
incognita excepto la última columna que contiene los términos independientes.

1
le corresponde la matriz de coeficientes 
Ejemplo 1.2. Al sistema lineal
4
4x + 5y = 6
x + 2y = 3
2
3
5 6

.
Las operaciones descritas al principio de la sección que se realizan sobre las ecuaciones de un sistema lineal en
el método de eliminacón se traducen en operaciones de fila sobre matrices, llamadas operaciones elementales de
fila, las cuales describimos a continuación.
6
Definición 1.2. Sea A una matriz de tamaño m × n, una operación elemental de fila sobre A es una de
las siguientes operaciones:
1. Multiplicar una fila por una constante no cero. Se usará la notación cFi → Fi para indicar que se multiplica
la fila i por la constante c.
2. Sumar un múltiplo de una fila a otra fila. Se usará la notación cFi + Fj → Fj para indicar que se le suma
c veces la fila i a la fila j.
En estos dos pasos, la fila que aparece después de la flecha es la fila que se debe modificar o simplemente,
a la que se le debe aplicar la operación.
3. Intercambiar dos filas. Se usará la notación Fi ↔ Fj para indicar que se debe intecambiar la fila i con la
fila j.
x + 3y = 4
Ejemplo 1.3. Al principio de la sección resolvimos el sistema de ecuaciones
aplicando las opera-
4x + 6y = 10
ciones
1. -4 Ecuación 1.1 más Ecuación 1.2, de la cual obtenemos la ecuación −6y = −6,
2. multiplicamos esta última ecuación por − 61 , obteniendo y = 1,
3. finalmente de, -3 ecuación (y = 1) más Ecuación 1.1, obtenemos x = 1.
Como en la matriz asociada a un sistema lineal las ecuaciones se representan en filas, estas operaciones se
traducen en operaciones de fila, de hecho, la primera operación se traduce en la operación de fila −4F1 + F2 , la
segunda en
−1
6 F2
y la tercera en −3F2 + F1 . Al aplicar estas operaciones obtenemos






1 3 4 −3F2 +F1 →F1 1 0
1
3
4
1 3 4







0 1
4 6 10 −4F1 +F2 →F2 0 −6 −6 −1 F2 →F2 0 1 1

6
1
1


De esta última matriz obtenemos las ecuaciones x = 1 y y = 1 las cuales nos dan la solución al sistema.
Este último ejemplo ilustra el método de solución de un sistema lineal con operaciones de fila sobre matrices, el
cual es el objetivo de la sección. Para ilustrar el caso general debemos mostrar como aplicar operaciones de fila
sobre una matriz de una manera eficiente que garantice una solución, una manera efectiva es llevar la matriz a
una “matriz en forma escalonada reducida”, la cual definimos a continuación.
Definición 1.3. Sea A una matriz de tamaño m × n, decimos que A está en forma escalonada reducida si
A satisface las siguientes condiciones:
1. Todas las filas nulas (filas donde todas las entradas, en esa fila, son ceros) están en la parte inferior de
la matriz.
2. La primera entrada no cero de una fila no nula es un uno. A esta entrada se le llama pivote.
3. Si dos filas consecutivas son no nulas, entonces el pivote de la fila de arriba está mas a la izquierda del
pivote de la fila de abajo.
7
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
4. Todas las entradas de una columna donde haya un pivote son cero, excepto la entrada donde está el pivote.
Ejemplo 1.4.

1


A = 0

0
Las siguientes matrices están


0 0
1 0




B = 0 1
1 0 ,


0 1
0 0

1 ∗


E = 0 0

0 0

∗


0 ,

0
en forma escalonada reducida:



∗
1 ∗ 0






C =  0 0 1 ,
∗ ,



0
0 0 0

0


F = 0

0
1 ∗



0 0

0 0
y


0 1


D = 0 0

0 0
0 0


G = 0 0

0 0

1


0 ,

0

0


1 ,

0
donde las entradas * representan un número real arbitrario. De hecho estas son todas las posibles formas escalonadas reducidas que se obtienen de matrices 3 × 3 no nulas.
Ejemplo 1.5. (MatLab) La forma escalonada reducida
de

−1
2


“rref ” como se muestra a continuación. Sea A =  0
3

2 −1
>> format rat, A = [−1, 2, 3, −1; 0, 3, −2, −1; 2, −1, −8, 1]; R
R=
1
0
0 − 13
3
1
− 32
una matriz
 se calcula en MatLab con el comando
3 −1


−2 −1,

−8
1
= rref (A)
1
3
− 31
0 0
0
0
El comando “format rat” se usa para que MatLab entregue la respuesta con números racionales en cada entrada
de la matriz.
El proceso de aplicar operaciones elementales de fila sobre una matriz hasta llevarla a su forma escalonada
reducida se le conoce como reducción Gauss-Jordan. Este proceso nos lleva también a determinar si el
sistema tiene solución y a encontrarla en el caso de que exista (ver Teorema 1.2). Primero debemos garantizar
que es posible llevar cualquier matriz a una matriz en forma escalonada reducida por medio de operaciones
elementales.
Teorema 1.1. Aplicando reducción Gauss-Jordan, toda matriz se puede llevar a una forma escalonada reducida.
Mas que dar una idea de la prueba, lo que presentamos a seguir, es una descripción de un algoritmo para
calcular la forma escalonada reducida de una matriz.
Bosquejo de la demostración. La demostración se hace por inducción sobre el número de columnas de A.
Si A tiene una columna y A = 0 entonces A ya está en forma escalonada reducida. Si A 6= 0 tomamos
ai1 la primera entrada no nula de A para algún i, entonces intercambiamos la primera fila con la i-ésima fila
8
obteniendo la matriz
ai1
0


 .. 
 . 
 0 .
 ai+1,1 
 . 
..
(1.3)
am1
Para reducir esta matriz, multiplicamos la primera fila por
1
ai1
obteniendo una matriz con un uno en la primera
posición y a continuación se usa esta entrada para anular el resto de las entradas como se muestra a continuación

ai1
0

 .. 
 . 
 0 
 ai+1,1 
 . 
..
1
ai1

1
0

 .. 
 . 
 0 
 ai+1,1 
 . 
..
F1 →F1
am1
1
0
−ai+1,1 F1 +Fi+1 →Fi+1
am1
..
.
−am1 F1 +Fm →Fm
 .. 
.
0
0
.
..
0
como esta última está en forma escalonada reducida obtenemos el resultado para matrices con una columna.
Ahora supongamos que el resultado es cierto para matrices con n − 1 columnas y sea A una matriz con n
columnas, usando la inducción obtenemos que podemos reducir las primeras n − 1 columnas hasta obtener una
matriz en la forma
1
... 0 ... 0
0 ... 1 ... 0
. . .. . . ..
.. ..
.
 ..
0

0
.
..
a1n
a2n
..
.




... 0 ... 1 akn  .
... 0 ... 0 ak+1,n 
. . .. . . .. .. 
.. .. .
0 ... 0 ... 0
amn
Si las entradas ak+1,n , . . . , amn son todas iguales a cero, entonces esta última matriz ya está en forma escalonada
reducida, en caso contrario, suponemos sin pérdida de generalidad que ak+1,n 6= 0, ya que si esta es cero haciendo
un intercambio de fila podemos llevar una entrada diferente de cero que este por debajo de ésta, como se hizo
en (1.3), después multiplicamos la fila k + 1 por
1
... 0 ... 0
0 ... 1 ... 0
.
 ..
0

0
.
..
. . .. . . ..
.. ..
a1n
a2n
..
.
obteniendo
1




... 0 ... 1 akn 
... 0 ... 0 ak+1,n 
. . .. . . .. .. 
.. .. .
0 ... 0 ... 0
1
ak+1,n
... 0 ... 0 a1n
0 ... 1 ... 0 a2n
1
ak+1,n
Fk+1 →Fk+1
. . . .
 . .. . ..
.
.
 0 ... 0 ...
 0 ... 0 ...
. . . .
.. . . .. . .

.. .. 

. . 
1 akn 
0 1 
.. .. 
. .
0 ... 0 ... 0 amn
amn
Finalmente, usando este 1, empleamos operaciones elementales para anular las demás entradas de esta columna
como se muestra a continuación
1
... 0 ... 0 a1n
0 ... 1 ... 0 a2n
. . . .
 . .. . ..
.
.
 0 ... 0 ...
 0 ... 0 ...
. . . .
.. . . .. . .
.. ..
. .
1 akn
0 1
.. ..
. .
0 ... 0 ... 0 amn
− a 1 Fk+1 +F1 →F1
1n







− a 1 Fk+1 +F2 →F2
2n
−a
..
.
− a 1 Fk+1 +Fk →Fk
kn
1
Fk+1 +Fk+2 →Fk+2
k+2n
..
.
1
Fk+1 +Fm →Fm
− amn
... 0 ... 0 0 
0 ... 1 ... 0 0
1
 ..
.
0
0
.
..
. . .. . . .. .. 
. . . . .
... 0 ... 1 0  ,
... 0 ... 0 1 

. . .. . . .. ..
.. ...
0 ... 0 ... 0 0
como esta última matriz está en forma escalonada reducida obtenemos por inducción que cualquier matriz se
puede reducir a una matriz en forma escalonada reducida.
9
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

1




Ejemplo 1.6. Calcular la forma escalonada de reducida de la matriz A = 2 2 1 4 .


3 3 2 6
Aunque sabemos que podemos usar MatLab para calcular esta reducción, es importante también entender

0
0 1
el algoritmo propuesto en el teorema anterior, el cual basicamente nos dice que la reducción la podemos hacer
columna por columna.
Como la primera columna no es nula pero su primera entrada es cero, entonces intercambiamos la fila
cuya primera entrada sea no nula, en este caso la segunda fila, como esto se debe hacer usando operaciones
elementales, entonces intercambiamos la

0


2

3
primera y la segunda fila


2 2
0 1 1
F ↔ F 
2
 1
0 0
2 1 4


3 3
3 2 6
Luego multiplicamos la primera fila por
este pivote para anular

2


0

3
1
2
1 4



1 1

2 6
para obtener el pivote en la primera columna y después usamos
las demás entradas de esta columna, como se muestra a




1
2 1 4 21 F1 → F1 1 1 12 2








0
 0 0 1 1
0 1 1




3 2 6
3 3 2 6 −3F1 + F3 → F3 0
continuación

1 21 2


0 1 1 .

0 12 0
El pivote en la segunda columna, si existiera, deberı́a estar en una fila debajo de la primera y como la segunda
y tercera entrada son ceros, entonces no hay pivote en esta columna, por tanto la tercera entrada en la segunda
fila es el siguiente pivote, usamos

1


0

0
esta entrada para anular las demás


1 12 2 − 21 F2 + F1 → F1 1 1




0 0
0 1 1


0 12 0 − 21 F2 + F3 → F3 0 0
entradas en la tercera columna, ası́

3
0
2

1
1 .

0 − 12
Finalmente, la cuarta entrada en la tercera fila debe ser el siguiente pivote, para convertirlo en un uno,
multiplicamos la tercera fila por -2 y después usamos el pivote para anular las demás entradas en la cuarta
columna, esto lo hacemos de la siguiente forma

1 1 0

3
2

1 1
0


+ F1 → F1 1



1  −F3 + F2 → F2 0


1
0
3
3
2  − 2 F3
1 0 0








(1.4)
0 0 1
0 0 1
1
0 1 0 .




0 0 0 − 12 −2F3 → F3 0 0 0
0 0 1


1 1 0 0




Por tanto la matriz 0 0 1 0 es la forma escalonada reducida de A.


0 0 0 1
El algoritmo anterior es el que se deduce del bosquejo de la demostración del teorema anterior, en donde
se calculan los pivotes columna por columna, otra forma de aplicar reducción Gauss-Jordan es calculando los
pivotes fila por fila en donde se debe aplicar la definición paso a paso.
10
Por ejemplo, si queremos calcular la forma escalonada reducida de la matriz A de esta forma, nótese que el
pivote en cada fila debe ser la primera entrada no nula de la fila, por tanto la tercera entrada de esta fila debe
ser el primer pivote, luego usamos esa entrada para anular las demás entradas en su respectiva columna como
se indica a continuación

0


0 0
1




4 −F1 + F2 → F2 2 2


6 −2F1 + F3 → F3 3 3
0 1


2

3
2 1
3 2
1 1



0 3 .

0 4
Con estos pasos estamos garantizando el cumplimiento de la condiciones 2. y 4. de la Definición 1.3.
El siguiente paso es encontrar el pivote en la segunda fila convertirlo en un uno y usarlo para anular las
restantes entradas en su respectiva columna. Para la segunda fila se tiene que el pivote corresponde a la primera
entrada en esta fila, para convertirlo en un 1 se multiplica la segunda fila por

0


2

3
0 1
2 0
3 0


1
0 0



1
3 2 F2 → F2 1 1


3 3
4

1
1
0
3
.
2
0
4
1
2

después se usa el pivote para anular las demás entradas en su columna, en este caso, la primera columna.

0 0 1


1 1 0

3 3 0
1



0


1

4 −3F2 + F3 → F3 0
3

2

0 1
1
1 0
3
.
2
− 21
0 0

Antes de continuar con el siguiente pivote notemos que los pivotes en esta última matriz no satisfacen la
condición 3. de la Definición 1.3, ya que el pivote de la segunda fila está a la derecha del primer pivote y no a
la izquierda, para organizarlos, intercambiamos las dos primeras filas:

0 0


1 1

0 0


1 F1 ↔ F2 1 1



3

0 0
0
2

1
0 0
0 −2
1

3
2
0

1 .

1
0 − 21
Finalmente observamos que la primera entrada no nula de la tercera fila es la última entrada en esta fila, para
convertirla en un uno y anular la otras entradas
de la última columna repetimos los pasos que hicimos en (1.4)

1 1 0 0




y obtenemos nuevamente que la matriz 0 0 1 0 es la forma escalonada reducida de A.


0 0 0 1

2 4


Ejemplo 1.7. Calcule la forma escalonada reducida de la matriz A = 2 4

1 2

−2


2 .

1
11
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Las operaciones para reducir esta matriz son las siguientes:


→ F1 1 2 −1








2 4
2 4
2  −2F1 + F2 → F2
2




1 2
1 −F1 + F3 → F3
1 2
1


1 2 0
F2 + F1 → F1




0 0 1 .


−2F1 + F3 → F3 0 0 0

2
4 −2

1
2 F1

1 2


0 0

0 0

−1


4

2
1
4 F2

1 2


→ F2  0 0

0 0

−1


1

2
Ahora que sabemos que toda matriz se puede llevar, por medio de operaciones elementales, a una matriz en
forma escalonada reducida, debemos también saber para que nos sirve este resultado en términos de soluciones
de sistemas de ecuaciones lineales. El siguiente teorema nos muestra la utilidad de poder reducir matrices a su
forma escalonada reducida ya que de esta última podemos determinar si un sistema tiene soluciones y en el caso
afirmativo también nos permite saber si la solución es única o existen infinitas.

a11 x1 + · · · + a1n xn = b1
a11

..
 .
Teorema 1.2. Considere el sistema de ecuaciones
, sea A =  ..
.


b1

.. 
. 

am1 x1 + · · · + amn xn = bm
am1 · · · amn bm
la matriz de coeficientes asociada al sistema y sea A′ la forma escalonada reducida de A. Tenemos los siguientes
···
..
.
a1n
..
.
casos:
1. Si A′ tiene pivote en todas las columnas excepto la última entonces el sistema tiene solución única.
2. Si A′ tiene pivote en la última columna entonces el sistema tiene solución vacı́a.
3. Si A′ no tiene pivote en la última columna y hay al menos otra columna sin pivote entonces el sistema
tiene infinitas soluciónes.

1 ··· 0

.
.

Demostración.
1. En este caso tenemos que A′ =  .. . . . ..

0 ··· 1
al final, las cuales omitimos al no aportar ninguna información

c1

.. 
y posiblemente algunas filas de ceros
.

cn
adicional.
De esta matriz se obtienen las ecuaciones x1 = c1 , . . . , xn = cn la cuales corresponden a la única solución
al sistema.
2. Como A′ tiene un pivote en la última columna y un pivote es la primera entrada no nula de una fila
h
i
entonces tenemos que la matriz A′ tiene una fila de la forma 0 · · · 0 1 y de esta fila se obtiene la
ecuación 0 = 1, lo cual implica que el sistema es inconsistente.
3. Supongamos sin pérdida de generalidad que las dos últimas columnas de A′ no tienen pivote y que las
12
demás si, entonces A′ tiene la forma

1

.
A′ =  ..

0
···
..
.
0
..
.
c1
..
.
···
1 cn−1
d1
..
.
dn−1





y posiblemente algunas filas cero de las cuales precindimos. Ası́ obtenemos las ecuaciones x1 + c1 xn =
d1 , . . . , xn−1 + cn−1 xn = dn−1 o equivalentemente
x 1 = d1 − c 1 x n ,
...,
xn−1 = dn−1 − cn−1 xn .
Las cuales corresponden a las soluciones del sistema y por cada valor asignado a la variable xn obtenemos
una solución, por tanto el sistema tiene infinitas soluciones.
Un razonamiento similar demuestra esta afirmación cuando la columna sin pivote está en una columna
diferente y también en el caso en donde hay varias columnas sin pivotes.
A las variables correspondientes a columnas sin pivote se les llamará variables libres y a las demás se les
llamará variables básicas o no libres. La siguiente obervación nos servirá más adelante.
Observación 1.1. Los recı́procos de las tres afirmaciones del teorema anterior también son ciertos, en la
Sección 1.4 veremos que las operaciones elementales de fila son reversibles lo cual permite aplicar operaciones
elementales de fila a A′ hasta recuperar la matriz A lo que nos lleva de las soluciones al sistema original.
Corolario 1.3. Un sistema lineal con más variables que ecuaciones (n > m) nunca tiene solución única.
Ejemplo 1.8. En este ejemplo se muestra las posibles soluciones para sistemas 2 × 2 según sus matricces
escalonadas reducidas.
x + 2y = 3
le corresponde la matriz de coeficientes
4x + 5y = 6




1 0 1
1 2 3
. Por el Teorema 1.2 el sistema tiene so y que la matriz escalonada reducida era 

0 1 1
4 5 6
lución única y esta dada por x = 1 y y = 1, la cual se muestra en la Figura 1.1.


1
1
4
4
x
+
y
=
1
3
3
2. Al sistema lineal 3
y su matriz escalonada
le corresponde la matriz de coeficientes  3
1
1
1
1
x
+
y
=
1
3 
3
3
3

1 3 0
. Por el Teorema 1.2 el sistema tiene solución vacı́a, lo cual se muestra en la Figura
reducida es 
0 0 1
1.1.


1 3 3
x + 3y = 3
 y su matriz escalonada
le corresponde la matriz de coeficientes 
3. Al sistema lineal
2 6 6
2x + 6y = 6
1. En el Ejemplo 1.3 se obtuvo que al sistema lineal
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

reducida es 
1
3 3
0
0 0
Figura 1.1.
13

. Por el Teorema 1.2 el sistema tiene infinitas soluciones, lo cual se muestra en la
Ejemplo 1.9. Determine si el sistema
de forma paramétrica.
x1 + x2 + x3 + x4 = 4
tiene soluciones y en el caso afirmativo escribalas
x3 − x4 = 3

Solución. La matriz de coeficientes es 
1 1
1
1
4
0 0
1 −1 3

 y su forma escalonada reducida está dada por A′ =

1
. Por el Teorema 1.2 el sistema tiene infinitas soluciones las cuales se pueden dar en forma

0 0 1 −1 3
paramétrica leyendo el sistema de ecuaciones de la matriz A′ , las cuales son x1 + x2 + 2x4 = 1 y x3 − x4 = 3,

1 1
0
2
y escribiendo las variables básicas en términos de las variables libres obtenemos
x1 = 1 − x2 − 2x4
x3 = 3
+ x4 .
De acuerdo a estas ecuaciones las variables x2 y x4 toman valores arbitrarios y por cada par de valores que se le
asignen a estas variables, se tiene una solución particular, si a estas variables les asignamos valores paramétricos
x2 = t y x4 = u obtenemos todas las soluciones paramétricas al sistema:
x1 = 1 − t − 2u
x2 = t
x3 = 3 + u
x4 = u.
Ejemplo 1.10. Considere el sistema

−1
2


 0
3

2 −1
3
−1

−x + 2y + 3z = −1
3y − 2z = −1 . La matriz asociada al sistema está dada por A =
2x − y − 8z = 1


−2 −1 cuya forma escalonada reducida R fué calculada en en el Ejemplo 1.5

−8
1


1
1 0 − 13
3
3



R = 0 1 − 32 − 31  .


0 0
0
0
De aquı́ tenemos que el sistema tiene infinitas soluciones las cuales estan dadas por
x=
1
3
+
13
3 z
y = − 31 + 23 z,
14
asignando el valor paramétrico z = t a la variable libre z, obtenemos las soluciones paramétricas al sistema:
x=
1
3
+
13
3 t
y = − 13 + 32 t
z=
t
−x + 2y + 3z = −1
Ejemplo 1.11. (MatLab) El sistema 2x − 4y − 6z = −1 tiene matriz asociada al sistema dada por
2x − y − 8z = 1

−1
2
3 −1




A =  2 −4 −6 −1 .


2 −1 −8
1
Usando MatLab para calcular la forma escalonada reducida de A,

(>>format rat, A = [−1, 2, 3, −1; 2, −4, −6, −1; 2, −1, −8, 1]; R = rref (A)), obtenemos la matriz


1 0 − 13
0
3




2
R =  0 1 − 3 0 .


0 0
0 1
Como esta última matriz tiene un pivote en la última columna, entonces por el Teorema 1.2 el sistema no tiene
solución.
Del Teorema 1.2 también se desprende el siguiente corolario, para el cual necesitamos la siguiente definición.
Definición 1.4. Un sistema lineal homogéneo es un sistema lineal de la forma
a11 x1 + · · · + a1n xn = 0
..
,
.
am1 x1 + · · · + amn xn = 0
es decir, un sistema donde todos los términos independientes son cero.
Corolario 1.4. Un sistema lineal homogéneo siempre tiene solución.
Terminamos la sección con la definición de rango de una matriz.
Definición 1.5. Sea A una matriz y A′ su forma escalonada reducida. Definimos el rango de A, denotado por
rango(A), como el número de pivotes de A′ .
Ejemplo 1.12. Para las matrices del Ejemplo 1.4 se tiene que
rango(A) = 3, rango(B) = rango(C) = rango(D) = 2 y
rango(E) = rango(F ) = rango(G) = 1.
15
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Problemas
1.1.1. Use el método Gauss-Jordan para resolver los siguientes sistemas.
a.
d.
x − 2y + 3z = 7
2x + y − z = 7
b.
2x + 4y − 4z = 6
2x − 5y + 4z = 6
2x − y − z = 7
−x + 16y − 14z = −3
x + 2y + 3z = 1
x + 2y + 3z + w = 7
4x + 5y + 6z = 2
e.
4x + 5y + 6z + 2w = 7
c.
x−y+z =4
2x + y + z = 3
x + 2y + 3z + 4w = 1
f.
7x + 8y + 9z + 4w = 7
7x + 8y + 9z = 4
x+y−z =7
x + 2y + 3z + 3w = 2
x + 2y + 2z + 2w = 3
x+ y+ z+ w =1
1.1.2. Encuentre las soluciones paramétricas al sistema y úselas para calcular dos soluciones particulares:
x − 2y + 3z + w = 3
y
=2
w=1
1.1.3. Demuestre que el sistema
2x − y + 3z = α
3x + y − 5z = β
es consistente si y sólo si λ = 2α − 3β.
−5x − 5y + 21z = λ
1.1.4. Para los sistemas cuyas matrices aumentadas están dadas en los numerales desde a. hasta c. determine
los valores α y β para los cuales el sistema tiene:
I. Ninguna solución.
II. Solución única.
III. Infinitas

1


a. 0

0
soluciones y en este caso dar dos soluciones particulares.



1 0
α
0
0
α
0







 b. 0 1
β
1
1
β
1



0 0 2α + β α + β − 1
0 α+β α−β−2
1.1.5. Muestre que el sistema
ax + by = 0
cx + dy = 0
c.

1 0


0 1

0 0
α
β
α−β
0





α−β−2
1
tiene solución si y sólo si ad − bc = 0.
1.1.6. Haga una lista de todas las matrices 3×4 que esten en forma escalonada reducida.
1.1.7. Demuestre el Corolario 1.3 y el Corolario 1.4.
1.1.8. Muestre que si el número de ecuaciones en un sistema lineal homogéneo es menor que el número de sus
incógnitas, entonces el sistema tiene una solución no trivial.
16
1.1.9. Muestre que efectuar operaciones elementales en un sistema de ecuaciones produce un sistema ecuaciones
equivalente. Dos sistemas de ecuaciones son equivalentes si tienen las mismas soluciones.
1.1.10. Usando el Problema 1.1.9, muestre que un sistema de ecuaciones es equivalente al sistema de ecuaciones
que se obtiene de la correspondiente matriz escalonada reducida.
1.1.11. Si A es una matriz de tamaño m × n, demuestre que el rango(A) ≤ mı́n{m, n}.
1.1.12. Demuestre que el sistema homogenéo
ax + by = 0
tiene infinitas soluciones si y sólo si ad − bc = 0
cx + dy = 0
1.2.
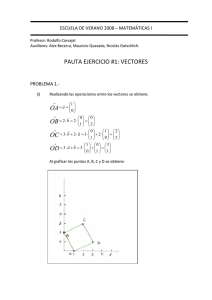
Operaciones con Matrices y Vectores
En esta sección se expondrán las operaciones básicas entre matrices y vectores y se mostrarán las propiedades
que estas operaciones satisfacen.
Definición 1.6. Definimos vector columna (fila) como una matriz con una sola columna (fila).
 
1
 
h
i
 
Ejemplo 1.13. v =  2  es un vector columna y w = 0 1 es un vector fila.
 
−1
Definición 1.7. (Operaciones con matrices y vectores)



a11 · · · a1n
b11



.. 
 .
 .
..
1. (Suma de matrices) Sean A =  ..
y B =  ..
.
. 



am1 · · · amn
bm1
definimos la matriz A + B como la matriz dada por:



A+B =

···
a11 + b11
..
.
···
..
.
a1n + b1n
..
.
am1 + bm1
···
amn + bmn
Similarmente, definimos la suma de los vectores x =

..
x
.
 1

xn

b1n

.. 
matrices del mismo tamaño,
. 

bmn
···
..
.



.




x 1 + y1
y1


 
..


.
y y =  ..  como el vector x + y = 
.
.


 
x n + yn
yn

" a1 #
..
Identificando vectores v =
con el vector en Rn iniciando en el origen y terminando en el punto
.
an
(a1 , . . . , an ), obtenemos que la suma de vectores se rige por la “Ley del paralolegramo”, ver
1.7. En la

 Figura
 
a
 1
a1


siguiente figura vemos la representación geométrica de los vectores v =   en R2 y w = a2  en R3 .


a2
a3
17
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO


a11 · · · a1n


.. 
 .
..
2. (Producto de una matriz por un escalar) Sea A =  ..
una matriz de tamaño m × n y α un
.
. 


am1 · · · amn
escalar (constante real arbitraria), definimos la matriz α · A como la matriz dada por

αa11

 ..
αA =  .

αam1
···
..
.
···

αa1n

.. 
.
. 

αamn

x1
 
 . 
Similarmente, definimos el producto de un vector x =  ..  por un escalar α ∈ R como el vector αx =
 
xn


αx1


 .. 
 . .


αxn

1
2



−2 −2






Ejemplo 1.14. (MatLab) Sean A = −1 −3 y B =  3



1
0
1
2A en MatLab como sigue



1 . Podemos calcular las matrices A + B y

1
>> A = [1, 2; −1, −3; 0, 1]; B = [−2, −2; 3, 1; 1, 1]; A + B, 2 ∗ A
Obteniedo las matrices:

−1


A+B = 2

1
0



−2

2

2
4





2 ∗ A = −2 −6 .


0
2
y
Notación 1. Denotaremos por Omn a la matriz de ceros de tamaño m × n, o simplemente por O si no hay
lugar a confusión y al vector cero lo denotaremos por θn o simplemente θ si no hay lugar a confusión.
Si A es una matriz, denotamos por Ai el vector fila formado por la i-ésima fila de A y por Ai el vector
columna formado por la i-ésima columna de A.
El siguiente teorema establece las propiedades que satisfacen estas operaciones en matrices y vectores.
Teorema 1.5. Sean A, B y C matrices de tamaños m × n, α y β escalares, entonces tenemos
1.
(A + B) + C = A + (B + C)
2.
A + Omn = Omn + A = A
3.
A + (−1A) = −1A + A = O
4.
A+B =B+A
5.
α(A + B) = αA + αB
6.
(α + β)A = αA + βA
7.
(αβ)A = α(βA)
8.
1A = A
18
De la Propiedad 3. de este teorema se observa que −1A es el inverso aditivo de A y este será denotado por
−A (el inverso aditivo de una matriz es único, ver Problema 1.2.4 ). En este sentido la diferencia de dos matrices
A y B, A − B, se define como: A + (−B).
El siguiente teorema establece las propiedades análogas que se cumplen para vectores.
Teorema 1.6. Sean x, y y z vectores con n componentes, α y β escalares, entonces tenemos
1.
(x + y) + z = x + (y + z)
2.
x + θn = θn + x = x
3.
x + (−1x) = −1x + x = θn
4.
x+y =y+x
5.
α(x + y) = αx + αy
6.
(α + β)x = αx + βx
7.
(αβ)x = α(βx)
8.
1x = x
A continuación se da la definición de producto interno de vectores y transpuesta de una matriz, lo cual
permitirá definir el producto de matrices.
 
 
x1
y1
 
 
 .. 
 .. 
Definición 1.8. Sean x =  .  y y =  .  vectores columna de n componentes, definimos el producto
 
 
xn
yn
interno o producto escalar de los vectores x y y, denotado por x · y, por la fórmula
x · y = x 1 y1 + · · · + x n yn =
n
X
x i yi .
i=1


a11 · · · a1n


.. 
 .
..
Definición 1.9. Sea A =  ..
 una matriz de tamaño m × n, definimos la matriz transpuesta
.
.


am1 · · · amn
de A, denotada por At , como la matriz cuyas columnas son las filas de A, esto es:

a11

.

At =  ..

a1n
···
..
.
···

am1

.. 
.
. 

amn
Si una matriz A satisface que At = A, decimos que A es simétrica.
Si una matriz A satisface que At = −A, decimos que A es antisimétrica.




2 1


2 3 −1

 entonces At = 
Ejemplo 1.15. Si A = 
 3 2 .


1 2
1
−1 1


2 −1
1




Si B = −1
2 −1 entonces B t = B y B es una matriz simétrica.


1 −1
2
19
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Ejemplo1.16. (MatLab)El comando en MatLab para calcular la transpuesta de una matriz es “transpose”.
32 −10
78




Sea A =  3
56 −89, ası́ para calcular su transpuesta se hace:


45
0
9
>> A = [32, −10, 78; 3, 56, −89; 45, 0, 9]; T = transpose(A)


32
3 45




Obteniedo la matriz T = At = −10
56 0 .


78 −89 9
Ahora pasemos a definir el producto de matrices.

a11 · · · a1n


.. 
 .
..
Definición 1.10. (Producto de matrices) Sea A =  ..
 una matriz de tamaño m × n y B =
.
.


am1 · · · amn


b11 · · · b1q


.. 
 ..
..
de tamaño n × q. Definimos el producto A · B, usualmente denotado por AB, como la matriz
 .
.
. 


bn1 · · · bnq


c11 · · · c1q


Pn
.. 
 .
..
de tamaño m × q dada por AB =  ..
 donde cij = k=1 aik bkj = ai1 b1j + ai2 b2j + · · · + ain bnj ,
.
.


cm1 · · · cmq
para i = 1, . . . , m y j = 1, . . . , q.

Notese que la ij-ésima entrada de la matriz AB es la suma de los productos de cada entrada en la fila i de A
por la respectiva entrada de la columna j de B, esto es:

a
 11
 .
 ..


 a
 i1
 .
 .
 .

am1
···
..
.
···
..
.
···

a1n

.. 
. 
  b11
 .
.
ain 

 .

.. 
.  bn1

amn
Este producto coincide con el producto escalar Ai
columna de B.
t
···
..
.
b1j
..
.
···
..
.
b1q
..
.
···
bnj
···
bnq



.

· Bj , donde Ai es la i-ésima fila de A y Bj es la j-ésima

Ejemplo 1.17. Calcular el producto AB donde A = 
1
−1
2
2
0


2

yB=
−2

−3
1

0


1 .

0
20
Solución. Vamos a calcular cada una de las entradas cij de la matriz AB:
     
2
1
2
h
it      
     
1 t
c11 = A · B1 = 1 −1 0 · −2 = −1 · −2 = 2 + 2 + 0 = 4,
     
1
0
1
     
0
1
0
h
it      
     
1 t
c12 = A · B2 = 1 −1 0 · 1 = −1 · 1 = 0 − 1 + 0 = −1,
     
0
0
0
     
2
2
2
h
it      
     
2 t
c21 = A · B1 = 2 2 −3 · −2 =  2  · −2 = 4 − 4 − 3 = −3,
     
1
−3
1
     
0
2
0
h
it      
     
2 t
c22 = A · B2 = 2 2 −3 · 1 =  2  · 1 = 0 + 2 + 0 = 2.
     
0
−3
0
De estos resultados tenemos

AB = 

Ejemplo 1.18. (MatLab) Sean A = 
1
2
podemos calcular el producto de matrices en
c11
c12
c21
c22


=
4
−1
−3
2

.

0


−1
0

 y B = 
−2 1 las matrices del ejemplo anterior,


2 −3
1 0
MatLab usando el comando “*”, como se muestra a continuación:


2
>> A = [1, −1, 0; 2, 2, −3]; B = [2, 0; −2, 1; 1, 0]; C = A ∗ B, D = B ∗ A
Obtienendo las matrices:


2

4 −1

 y D = 0
C=

−3
2
1
−2
0



−3 .

−1
0
4
El ejemplo anterior nos muestra que el producto de matrices no es en general conmutativo pero si satisface la
asociatividad.
Teorema 1.7. Sean A, B y C matrices de tamaños m × n, n × p y p × q, respectivamente. Entonces se tiene
que
A(BC) = (AB)C.
Demostración. Sean aij , bij y cij las entradas de las matrices A, B y C respectivamente, y sean dij y eij las
entradas de las matrices AB y BC respectivamente. Por definición del producto de matrices tenemos que
dij =
n
X
k=1
aik bkj
y
eij =
p
X
h=1
bih chj .
21
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Ahora, sean fij y gij las entradas de las matrices A(BC) y (AB)C respectivamente. Entonces
fij =
n
X
aik ekj =
k=1
gij =
p
X
h=1
n
X
aik
k=1
dih chj =
p
X
bkh chj =
h=1
p X
n
X
p
n X
X
aik bkh chj =
h=1 k=1
De las ecuaciones (1.5) y (1.6) tenemos que (AB)C = A(BC).
aik bkh chj
y
(1.5)
k=1 h=1
p
n X
X
aik bkh chj .
(1.6)
k=1 h=1
Una matriz con igual número de filas y columnas, es de decir de tamaño n × n, se llama matriz cuadrada.
El producto de matrices cuadradas satisface otras propiedades importantes, entre ellas la existencia de una
matriz neutra bajo
a la cual se le llama la matriz identidad y se denota por In . Esta matriz se

 el producto,
1 ··· 0


.
 .. . .
define por In =  .
. .. , es decir, la matriz identidad es la matriz cuyas entradas en la diagonal principal


0 ··· 1
son uno y ceros por fuera esta. Listamos a continuación más propiedades de las operaciones con matrices.
Teorema 1.8. Sean A y C matrices de tamaños m × n y n × q respectivamente, entonces se tiene lo siguiente:
1. Im A = A y AIn = A. En particular si A es una matriz cuadrada de tamaño n × n entonces AIn = In A = A.
2. Okm A = Okn y AOnk = Omk para cualquier k = 1, 2, 3, · · · . En particular si A es una matriz cuadrada de
tamaño n × n entonces AOnn = Onn A = Onn .
3. (A + B)C = AC + BC, donde B es una matriz de tamaño m × n.
4. A(B + C) = AB + AC, donde B es una matriz de tamaño n × q.
A continuación listamos tres propiedades, que aunque parecen no tener mucha importancia, serán muy útiles
en muchas demostraciones en el resto del libro.


A1


 . 
Lema 1.9. Sean A =  ..  una matriz de tamaño m × n donde A1 , . . . , Am son las filas de A, B =


Am
 
x1
 
h
i
 .. 
B1 · · · Bq de tamaño n × q donde B1 , . . . , Bq son las columnas de B y x =  .  un vector columna,
 
xq
entonces
1. Las columnas del producto AB son los vectores columna AB1 , . . . , ABq , es decir
h
i
AB = AB1 · · · ABq .


A1 B


 . 
2. Las filas del producto AB son los vectores fila A1 B, . . . , Am B, esto es, AB =  .. .


Am B
22
3. El producto Bx es el vector x1 B1 + · · · + xq Bq . Es decir, el vector Bx es una combinacion lineal de las
columnas de B con coeficientes tomados de x.
En el siguiente ejemplo se muestra como puede ser usado el lema anterior para realizar el producto de matrices.
 




2
 
1
0 3
1 −3

 y x = −3
, B = 
Ejemplo 1.19. Sean A = 
. El producto AB se puede ver de las
 
2 −1 1
4 −1
1
siguientes formas
h
i 
1 −3 B
i  y
AB =  h
4 −1 B
 
 
  
3
0
1
AB = A   A   A  
1
−1
2
 
 
 
  
−3
1
−3
1
= 1   + 2   0   − 1  
−1
4
−1
4


−5 3 0
.
=
2 1 11
 
 
−3
1
3   + 1  
−1
4
El producto Bx es una combinación de las columnas de B:
 
   
 
5
3
0
1
Bx = 2   − 3   + 1   =   .
8
1
−1
2
El producto de matrices sirve para establecer otra conexión entre matrices y sistemas de ecuaciones lineales. Sea
a11 x1 + · · · + a1n xn = b1
..
un sistema de ecuaciones lineales, entonces por definición del producto de matrices
.
am1 x1 + · · · + amn xn = bm


 
a11 · · · a1n
x1


 
.
 ..


..
..  , x =  ... 
tenemos que este sistema es equivalente a la ecuación matricial Ax = b donde A =  .

.


 
am1 · · · amn
xn
 
b1
 
 . 
y b =  ..  . En lo que sigue del libro usaremos la ecuación matricial Ax = b en lugar del sistema de ecuaciones.
 
bm
Terminamos la sección definiendo matrices triangulares y matriz diagonal, que aparecen muy a menudo en
varias partes del libro.

a11

 ..
Definición 1.11. Sea A =  .

an1
···
..
.
···

a1n

.. 
una matriz de tamaño n × n, decimos que
. 

ann
23
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
1. A es triangular superior si aij = 0 para i > j.
2. A es triangular inferior si aij = 0 para i < j.
3. A es diagonal si aij = 0 para i 6= j.



1 2 3
1 0






Ejemplo 1.20. Las matrices A = 0 3 1, B = 2 3



0 0 2
1 2
triangular superior, triangular inferior y diagonal.


0
1




0 y C = 0


2
0

0 0


3 0 son, respectivamente,

0 2
Problemas
 
 
−2
3
 
 
 
 
 
 
1.2.1. Ejecutar las operaciones indicadas con los vectores v = −1, w = 1 y z =  5 .
 
 
 
0
2
3

a.
A+B
b.
b.
3v
A−B
c.
− 3w

d. 3v + 2d − 3w.



−2 −2
1
2








1.2.2. Ejecutar las operaciones indicadas con las matrices A = −1 −3 y B =  3
1 .




1
1
0
1
a.
v+w
1
c.

− 3A
d.
− 3A + 2B.
1.2.3. Es muy posible que los estudiantes que esten tomando álgebra lineal por primera vez esten acostumbrados
a que al multiplicar dos cosas distintas de cero su resultado sea distinto de cero. En la multiplicación de matrices
esto puede no ocurrir. Al resolver este problema encontrarán ejemplos de esta situación y de otras situaciones
a las que posiblemente no esten acostumbrados.





1
3
3
0 1
, C = 
, B = 
Sean A = 
−1
52 52
0 0
los siguientes productos:




0
1 0
0
, E = 
, D = 
0
0 0
0
(a) AA, F F F y BC. ¿Puede concluir algo más general del producto BC?
(b) DD y EE.
1.2.4. Demuestre que el inverso aditivo de una matriz es único.
1.2.5. Sean A y B matrices de tamaños m × n. Muestre que
(a) (A + B)t = At + B t .
(b) (AB t )t = BAt .


0

0
yF =
0

1
0
1 0



0 1. Calcule

0 0
24
1.2.6. Sean A y B matrices de tamaños m × n y n × p, demuestre que (AB)t = B t At .
1.2.7. Demuestre los Teoremas 1.5, 1.6 y 1.8.
1.2.8. Una matriz cuadrada se llama una matriz de probabilidad si cada componente es no-negativa y la suma
de los elementos de cada fila es 1. Demuestre que si A y B son dos matrices de probabilidad tamaños m × n y
n × q, entonces AB es una matriz de probabilidad.
1.2.9. Si A y B son matrices simétricas demuestre lo siguiente
1. A + B es simétrica.
2. (AB)t = BA.
1.2.10. Si A es una matriz de tamaño m × n, demuestre que AAt y At A son matrices simétricas.
1.2.11. Sea A ∈ Mn (R), muestre que A+At es simétrica y A−At es antisimétrica y A = 21 (A+At )+ 21 (A−At ).
Es decir, toda matriz cuadrada se puede expresar como la suma de una matriz simétrica y una antisimétrica.
1.2.12. Sean A, B ∈ Mn (R), demuestre lo siguiente
1. Si A y B son triangulares superiores, entonces AB es triangular superior.
2. Si A y B son triangulares inferiores, entonces AB es triangular inferior.
3. Si A y B son matrices diagonales, entonces AB es diagonal.
4. En todos los anteriores casos, si las entradas en las diagonales principales de A y de B son, respectivamente, a11 , . . . , ann y b11 , . . . , ann , entonces las entradas en la diagonal principal de AB son a11 b11 , . . . , ann bnn .
" λ ··· 0 #
1
1.2.13. Sean A, B ∈ Mn (R) con B = .. . . . .. diagonal, demuestre lo siguiente:
.
.
0 ··· λn
1. Si las columnas de A son C1 , . . . , Cn entonces las columnas de AB son λ1 C1 , . . . , λn Cn . Es decir, si
A = [ C1 · · · Cn ] entonces AB = [ λ1 C1 · · · λn Cn ].
"F #
1
2. Si las filas de A son F1 , . . . , Fn entonces las columnas de BA son λ1 F1 , . . . , λn Fn . Es decir, si A = ..
.
Fn
"λ F #
1 1
..
.
entonces BA =
.
λn Fn
1.2.14. Si A ∈ Mmn (R), demuestre que rangoA = 1 si y sólo si existen vectores v ∈ Rm y w ∈ Rn tal que
A = vwt .
1.2.15. Sean v1 , v2 y v3 vectores en Rn y α un escalar. Demuestre lo siguiente:
v1 · θ = 0,
v1 · v2 = v2 · v1 ,
v1 · (v2 + v3 ) = v1 · v2 + v1 · v3 ,
(αv1 ) · v2 = v1 · (αv2 ) = α(v1 · v2 )
y
v1 · v2 ≥ 0.
1.2.16. Si A y B son matrices cuadradas que conmutan y son nilpotentes entonces A + B es nilpotente.
25
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
1.3.
Inversa de una Matriz
Las matrices invertibles juegan un papel fundamental en el álgebra lineal, en particular la posibibilidad de
tener la inversa de una matriz nos permitirá resolver algunos sistemas de ecuaciones lineales de manera muy
simple. Se comienza esta sección con la definición de este concepto.
Definición 1.12. Sea A una matriz cuadrada de tamaño n × n, decimos que A es invertible si existe una
matriz B de tamaño n × n tal que AB = BA = In .


2 1
 es invertible ya que el producto
Ejemplo 1.21. La matriz A = 
1 1

A

 
1 0
−1
 = I2 .
=
0 1
2

 
1
2 1
−1

=
−1
1 1
2
1
−1

Ejemplo 1.22. No toda matriz tiene inversa, por ejemplo, si la matriz A = 

entonces existirı́a una matriz B = 

tendrı́amos que 
a+b
c+d
0
0
invertible.

a
c
b
d

 = I2 = 

1 1
0 0

 tuviera una inversa,

 tal que AB = BA = I2 . Sin embargo AB = 
1 0
0 1
a+b
c+d
0
0


 y
, por tanto 0=1 lo cual es una contradicción y A no puede ser
En general si A es una matriz con una fila de ceros entonces A no es invertible. Esta afirmación se deja como
ejercicio, Problema 1.3.5.
Las matrices invertibles satisfacen las siguientes propiedades.
Lema 1.10. Sea A una matriz n × n una matriz invertible, entonces la inversa es única.
Demostración. Sean B y C matrices inversas de A, es decir
AB = BA = In
y
AC = CA = In .
Entonces utilizando una de las propiedades de la matriz identidad del Teorema 1.8 tenemos que:
B = BIn = B(AC) = (|{z}
BA )C = In C = C.
In
Notación 2. Como la inversa de una matriz invertible es única, entonces de ahora en adelante la denotaremos
por A−1 .
Teorema 1.11. Sean A y B matrices de tamaños n × n, entonces:
26
1. Si A y B son invertibles entonces AB es invertible y (AB)−1 = B −1 A−1 .
2. A es invertible si y sólo si At es invertible y en este caso se tiene que (At )
Demostración.
−1
t
= A−1 .
1. Utilizando la propiedad asociativa del producto de matrices (Teorema 1.7) se tiene que
−1 −1
−1
−1
(AB)(B −1 A−1 ) = A BB
| {z } A = AIA = AA = I
=I
y de igual forma (B −1 A−1 )(AB) = I, entonces la matriz B −1 A−1 es la inversa de AB. Como la inversa
es única tenemos que (AB)−1 = B −1 A−1 .
2. Supongamos que A es invertible, por el Problema 1.2.6 tenemos que At (A−1 )t = (A−1 A)t = I t = I y
además (A−1 )t At = (AA−1 )t = I t = I, entonces la matriz (A−1 )t es la invera de At , como la inversa es
única obtenemos que (At )−1 = (A−1 )t .
La demostración del recı́proco es análoga.

1 −1 3


1 −1 2









Ejemplo 1.23 (MatLab). Sean A = 1 −2 2 y B = 0
0 1, de acuerdo al teorema anterior hay




2
0 2
1 −2 2
dos maneras de calcular (AB)−1 , las cuales son multiplicar A y B y despues calcular su inversa, o calcular B −1
y A−1 y multiplicarlas. El comando para calcular la inversa de una matriz es “inv”, a continuación exhibimos
estos cálculos en MatLab.
>> format rat, A = [1, −1, 3; 1, −2,
= [1, −1, 
2; 0, 0, 1; 1, −2,2]; C = inv(A∗B), D = inv(B)∗inv(A)
 2; 2, 0, 2]; B 
−8
 3

Obteniendo las matrices C = − 34

1
3
7
3
2
3
− 23
7
6
−8
 3

5
 y D = − 34
6

1
6
1
3
7
3
2
3
− 23
7
6
5
,
6
las cuales son iguales.
1
6
El teorema también nos dice que hay dos maneras de calcular la inversa de At , una de forma directa y la
otra se obtiene al transponer A−1 .
>> format rat, A = [1, −1, 3; 1, −2, 2;
 2, 0, 2]; E = transpose(inv(A))


Obteniendo E = 

− 23
1
3
2
3

− 13  y si se calcula de la siguiente forma,

1
1
2
−
3
6
6
>> format rat, A = [1, −1, 3; 1, −2, 2; 2, 0, 2]; F = inv(transpose(A))
1
3
− 23
se obtiene lo mismo.
Si Ax = b es un sistema de ecuaciones con A invertible, entonces el sistema tiene solución única y esta es facı́l
de calcular como se muestra a continuación.
Teorema 1.12. Sea Ax = b un sistema de ecuaciones lineales de n ecuaciones con n incognitas. Si A es
invertible entonces el sistema tiene solución única y esta está dada por x = A−1 b.
27
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Demostración. Se deja como ejercicio.
x − y + 3z = 2
Ejemplo 1.24. (MatLab) Resuelva el sistema lineal x − 2y + 2z = 1.
2x
+ 2z = 0

 

2
3
 


 


Solución. El sistema es equivalente a la ecuación Ax = b con A = 1 −2 2 y b = 1 y de acuerdo al
 


0
2
0 2
teorema anterior la solución está dada por x = A−1 b la cual calculamos con MatLab
1 −1
>> A = [1, −1, 3; 1, −2, 2; 2, 0, 2]; b = [2; 1; 0]; x = inv(A) ∗ b
 
−1
 
 
Obteniendose el vector x =  0 . Entonces la solución al sistema está dada por x = −1, y = 0 y z = 1.
 
1
Problemas

1.3.1. Demuestre que una matriz A = 
a
b
c
d

 es su propia inversa si y sólo si A = ±I o a = −d y bc = 1 − a2 .
1.3.2. Encuentre cuatro matrices 2×2 que sean sus propias inversas.
1.3.3. Sea A una matriz m × n y sea B una matriz n × m con n < m, demuestre que AB no es invertible.
(Ayuda: Demuestre que existe x 6= 0 tal que ABx = 0.)
Sean A, B y C matrices de tamaño n × n.
1.3.4. Demuestre que si A = BC con A y B invertibles entonces C es invertible.
1.3.5. Demuestre que si una matriz A tiene una fila o una columna de ceros, entonces A no es invertible (Use
el Lema 1.9.)
1.3.6. Demuestre el Teorema 1.12.
1.3.7. Demuestre que A−1 es invertible y que (A−1 )−1 = A.
1.3.8. Si A es 4 × 3 y B es 3 × 4 muestre que AB 6= I. (Ayuda: Muestre que la ecuación Bx = 0 tiene una
solución no trivial.)
1.3.9. Generalizando el problema anterior, si A es m × n y B es n × m y m > n entonces AB 6= I.
28
1.4.
Matrices Elementales
En esta sección introduciremos las matrices elementales las cuales están asociadas a las operaciones elementales definidas en la Sección 1.
Definición 1.13. Sea E una matriz de tamaño n × n, decimos que E es una matriz elemental si E se obtiene
de la identidad al aplicar una operación elemental de fila.
Ejemplo 1.25. Las siguientes matrices son matrices elementales:





1
0
1 2 0
0 1 0










B = 0 1 0 y C = 0 −3
A = 1 0 0 ,





0
0
0 0 1
0 0 1

0


0 .

1
Cada una de estas matrices se obtiene al aplicar una operación sobre la matriz identidad, como se muestra a
conitunación:




0

0
1


0

0
y




0 1 0
0

F ↔ F 
2

 1
1 0 0 = A,
1 0



0 0 1
0 1



0
1 2 0
 2F + F → F 

1
1
 2

0 1 0 = B,
0



1
0 0 1
1 0
0
1
0
1 0


0 1

0 0


1
0




0
0
 −3F2 → F2 
0
1
0
0



−3 0 = C.

0 1
Notación 3. Como hay tres tipos diferentes de operaciones elementales, hay un número igual de tipos de
matrices elementales, entonces usaremos la siguiente notación.
Eij denotará la matriz elemental que se obtiene al intercambiar las filas i y j de la matriz identidad.
Eij (c) denotará la matriz que se obtiene al sumar c veces la fila i a la fila j de la matriz identidad.
Ei (c) la matriz que se obtiene al multiplicar por la constante c la fila i de la matriz identidad.
Ejemplo 1.26. En el ejemplo anterior tenemos que A = E12 , B = E21 (2) y C = E2 (−3).
La importancia de las matrices elementales reside en el hecho de que estas matrices reemplazan las operaciones elementales ya que aplicar una operación elemental a una matriz A es equivalente a multiplicar la matriz
elemental correspondiente a la operación por A. Esto lo expresamos en el siguiente teorema.
Teorema 1.13. Sea A una matriz de tamaño m × n y E una matriz elemental de tamaño m × m asociada a
una operación elemental de fila, el producto EA es la matriz que se obtiene al aplicar la operación elemental de
fila a la matriz A.
29
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
La demostración de este teorema se hace verificando que al aplicar una operación elemental se obtiene la
misma matriz que al multiplicar la matriz asociada a la operación elemental, se debe considerar un caso por cada
operación elemental. La verificación es sencilla y preferimos mostrar un ejemplo que compruebe la afirmación.

2 2


Ejemplo 1.27. Sea A = 0 1

4 5


1 1
2




la matriz 0 1 −1.


4 5
1
4



−1. Al aplicar la operación que multiplica la primera fila por

1

1
2
0
0
1
2
obtenemos




Nótese que la matriz elemental asociada a esta operación es la matriz E1 ( 12 ) =  0 1 0  y es fácil


0 0
1


1 1
2




verificar que E1 ( 12 )A = 0 1 −1.


4 5
1


2 2
4




Si en la matriz A sumamos -2 veces la fila 1 a la fila 3 obtenemos la matriz 0 1 −1.


0 1 −7


1 0 0




Nótese que la matriz elemental asociada a esta operación está dada por E13 (−2) =  0 1 0 y es fácil


−2 0 1


2 2
4




verificar que E13 (−2)A = 0 1 −1.


0 1 −7


2 2
4




Finalmente, si en la matriz A intercambiamos las filas 2 y 3 obtenemos la matriz 4 5
1 . La matriz


0 1 −1




2 2
4
1 0 0








elemental asociada a esta operación de fila es E23 = 0 0 1 y fácil ver que E23 A = 4 5
1 .




0 1 −1
0 1 0
Las operaciones elementales de fila son reversibles, es decir, al aplicar una operación elemental de fila, siempre
se puede aplicar otra operación elemental que deshaga la operación aplicada. Esto se muestra en el siguiente
ejemplo.
Ejemplo 1.28. Para ilustrar la reversibilidad de las operaciones elementales consideremos la matriz A =
30

3




 2 0 2, si intercambiamos las filas 1 y 2 de esta matriz y aplicaramos nuevamente la misma operación,


−3 1 0
obtenemos la matriz orginal como se muestra a continuación






0 1 3
2 0 2
0 1 3

F ↔ F 
F ↔ F 

2
2

 1
 1

 2 0 2
 0 1 3
 2 0 2 .






−3 1 0
−3 1 0
−3 1 0

0
1
En general, si se intercambian dos filas de una matriz, la operación se puede revertir al volver a intercambiarlas
una vez más. Esto a la vez nos dice que la matriz elemental Eij , asociada a esta operación de intercambio de
−1
= Eij .
dos filas, es invertible y es igual a su propia inversa, esto es Eij
Volviendo a la matriz A, si multiplicamos la fila 2 por
1
2
y después multiplicamos la misma fila por 2 obtenemos
la matriz original como se muestra a continuación



0 1
0 1 3





1
 2 0 2 2 F2 → F2  1 0



−3 1
−3 1 0



0 1 3
3






1 2F2 → F2  2 0 2 .



−3 1 0
0
En general, si se multiplica una fila de una matriz por una constante c 6= 0, la operación se puede revertir al
volver a multiplicar la misma fila de la nueva matriz por la constante
1
c.
Esto a la vez nos dice que la matriz
elemental Ei (c), asociada a esta operación de multiplicar la fila i por una constante c 6= 0, es invertible y su
inversa está dada por Ei (c)−1 = Ei 1c .
Una vez mas regresamos a la matriz A, si le sumaramos
1
2
la fila 2 a la fila 1 obtenemos la matriz original como se



1
0 1 3 2 F2 + F1 → F1
1 1






 2 0 2
 2 0



−3 1 0
−3 1
muestra a continuación


−1
4 − 2 F2 + F1 → F1
0




 2
2


0
−3
de la fila 2 a la fila 1 y después le sumaramos
−1
2
de

1 3


0 2 .

1 0
Comúnmente, si se le suma c veces la fila i de una matriz a la fila j, la operación se puede revertir al volver
a sumar −c veces la fila i a la fila j. Esto una vez mas nos dice que la matriz elemental Eij (c), asociada a
esta operación de sumar c veces la fila i a la fila j, también es invertible y su inversa está dada por Eij (c)−1 =
Eij (−c) .
De acuerdo a lo observado en el ejemplo anterior tenemos el siguiente resultado.
Teorema 1.14. Toda matriz elemental es invertible y las inversas estan dadas por
1
−1
.
= Eij ,
Eij (c)−1 = Eij (−c) y Ei (c)−1 = Ei
Eij
c
Al aplicar reducción Gauss-Jordan a una matriz, por cada operación elemental de fila, hay una matriz
elemental, la matriz que se obtiene al aplicar la operación de fila a la matriz identidad. Como toda matriz se
puede reducir a una forma escalonada reducida, entonces se tiene el siguiente teorema.
31
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Teorema 1.15. Toda matriz se puede expresar como el producto de un número finito de matrices elementales
por una matriz en forma escalonada reducida. Mas concretamente, si A es una matriz de tamaño m × n, existen
matrices elementales E1 , . . . , Ek todas de tamaño m × m y una matriz escalonada reducida A′ tal que
A = E1 · · · Ek A′ .
Demostración. El resultado se sigue de los Teoremas 1.1 y 1.13 teniendo en cuenta que a cada operación
elemental tiene asociada una matriz elemental.


1 1 0




Ejemplo 1.29. Expresar la matriz A = 1 1 2 como un producto de matrices elementales por una matriz


2 2 2
en forma escalonada reducida.
Solución. Necesitamos aplicar reducción Gauss-Jordan a la matriz A indicando las matrices elementales asociadas a

1


1

2
cada operación aplicada


1 0
1 1




1 2 −F1 +F2 →F2 0 0


2 2
2 2
| {z }
E12 (−1)


0
1




0
2


2 −2F1 +F3 →F3 0
{z
}
|
E13 (−2)
Por el Teorema 1.13 tenemos que E23 (−2)E2
tiene que
1
2


1 0
1




0 2 12 F2 →F2 0


0 2
0
| {z }
E2 ( 21 )
1 0


1 1 0







 0 0 1 .
0 1



0 2 −2F2 +F3 →F3 0 0 0
{z
}
|
E23 (−2)

1 1 0





E13 (−2)E12 (−1)A = A′ con A′ = 0 0 1. Entonces se


0 0 0
A = E12 (−1)−1 E13 (−2)−1 E2
−1
1
E23 (−2)−1 A′
2
= E12 (1)E13 (2)E2 (2)E23 (2)A′ .
Escribiendo las matrices de manera

1 0


A = 1 1

0 0
explicita tenemos:


0
1 0 0
1 0




0 0 1 0 0 2


1
2 0 1
0 0
A continuación verificamos el resultado con MatLab

0
1 0


0 0 1

1
0 2


0
1 1 0




0 0 0 1 .


1
0 0 0
>> E1=[1 0 0;1 1 0;0 0 1]; E2=[1 0 0;0 1 0;2 0 1]; E3=[1 0 0;0 2 0;0 0 1]; E4=[1 0 0;0 1 0;0 2 1]; A′ =[1 1
0;0 0 1;0 0 0]; A = E1 ∗ E2 ∗ 
E3 ∗ E4 ∗A′
1 1


Obteniendo la matriz A = 1 1

2 2
0


2 .

2
32
Ahora usaremos matrices elementales para dar un criterio de invertibilidad de una matriz. Primero debemos
observar lo siguiente.
Lema 1.16. Sea A una matriz de tamaño n × n en forma escalonada reducida, entonces A es invertible si y
sólo si A = I.
Demostración. “⇒”Supongamos que A es una matriz escalonada reducida invertible y razonemos por el
absurdo, supongamos que A 6= I, entonces A tiene al menos una columna sin pivote y al ser de tamaño n × n,
A debe tener al menos una fila de ceros, entonces por el Problema 1.3.5 A no puede ser invertible, lo cual es un
absurdo. Concluimos que A = I.
“⇐”Si A = I entonces A es claramente invertible.
De esto se desprende el siguiente resultado.
Teorema 1.17. Sea A una matriz de tamaño n × n, entonces A es invertible si y sólo si A se puede escribir
como un producto de matrices elementales.
Demostración. “⇒”Supongamos que A es invertible. Por el Teorema 1.15 sabemos que A = E1 · · · Ek A′
con E1 , . . . , Ek matrices elementales y A′ en forma escalonada reducida, como A es invertible y las matrices
elementales también son invertibles tenemos que A′ es invertible, entonces por el Lema 1.16 tenemos que A′ = I
y por tanto A = E1 · · · Ek es un producto de matrices elementales.
“⇐”Si A = E1 · · · Ek es un producto de matrices elementales, como las matrices elementales son invertibles
entonces A es el producto de matrices invertibles y por el Teorema 1.11 tenemos que A es invertible.


0
1
2




Ejemplo 1.30. Expresar la matriz A =  1
0
1  y su inversa como un producto de matrices elementales.


−1 −2 −2
Solución. Abajo se muestra la reducción Gauss-Jordan de esta matriz indicando la matriz elemental asociada
a cada operación aplicada de acuerdo a la Notación 3.

0


 1

−1
1
2


1

−1 −2
0

1


0

F2 +F3 →F3 0
| {z }
E23 (1)

F1 ↔F2
| {z }
0 1
E12



1 2

0 1

1


 0

−1
0
{z
E31 (−1)


1
}
1


0

0
0 0
1
0 0






1 2 −2F3 +F2 →F2 0


0 1
0
|
{z
}
E32 (−2)
De aquı́ tenemos que E32 (−2)E31 (−1)E23 (1)E13 (1)E12 A = I, por tanto
A−1 = E32 (−2)E31 (−1)E23 (1)E13 (1)E12
1


2

−1 −1
E13 (1)

1

0




0
2


−1 −2 F1 +F3 →F3 0
| {z }
1
−F3 +F1 →F1
|
1
y



1 0

0 1
33
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
−1
A = E12
E13 (1)−1 E23 (1)−1 E31 (−1)−1 E32 (−2)−1
= E12 E13 (−1)E23 (−1)E31 (1)E32 (2).
Las matrices elementales también nos ayudan a demostrar un algoritmo para calcular la inversa de una matriz,
el cual enunciamos a continuación.
Notación 4. Sea A y B matrices con el mismo número de filas, a la matriz obtenida de juntar ambas matrices
i
h
se llamará matriz aumentada y se denotará por A B .
Teorema 1.18. (Algoritmo para calcular la inversa de una matriz) Sea A una matriz invertible de tamaño n×n,
h
i
h
i
al aplicar reducción Gauss-Jordan a la matriz aunmentada A I obtenemos la matriz I A−1 . Más
i
h
aún, si B es una matriz de tamaño n × q, al aplicar reducción Gauss-Jordan a la matriz aumentada A B
h
i
obtenemos la matriz I A−1 B .
Demostración. Sean E1 , . . . , Ek las matrices elementales asociadas a las operaciones elementales necesarias
para reducir la matriz A a su forma escalonada reducida A′ . Como A es invertible entonces A′ = I y tenemos
h
i
que Ek · · · E1 A = I. Al aplicar las operaciones E1 , . . . , Ek a la matriz A | I obtenemos
E
E
E


k
2
1
 E k · · · E1 A | E k · · · E1  .
[E2 E1 A | E2 E1 ] → . . . −−→
[E1 A | E1 I = E1 ] −−→
[A | I] −−→
| {z }
(1.7)
=I
Como Ek · · · E1 A = I y como la inversa de una matriz cuadrada es única, entonces Ek · · · E1 = A−1 , ası́ la
h
i
última matriz en la Ecuación (1.7) es igual a I | A−1 .
El mismo análisis muestra la segunda parte.

0
1
2



1  calcular A−1 .

−2 −2


Ejemplo 1.31. (MatLab) Sea A =  1

−1
1
Solución. Usando MatLab para calcular la forma escalonada reducida de la matriz
>> AI = [0, 1, 2, 1, 0, 0; 1, 1, 1, 0, 1, 0; −1, −2, −2, 0,0,1]; rref (AI)
Obteniendo la matriz aumentada
−1
inversa A

0
2


= −1 −2

1
1
1
h
I
A



−2.

1

0
i
1 0


= 0 1

0 0
1


Ejemplo 1.32. (MatLab) Sean A =  1
1

−1 −2
2

0
0
0 −1
1
1

2
1
h
A I

i
obtenemos


−2 −2 , de lo cual se sigue que la matriz

1
1
1 2







1  y B = 2 3, calcular A−1 B.



0 1
−2
34
Solución. De acuerdo al teorema
anterior debemos encontrar la forma escalonada reducida de la matriz au
0
1
2 1 2

i 
h


mentada C = A B =  1
1
1 2 3 , la cual calculamos usando MatLab


−1 −2 −2 0 1
>> C = [0, 1, 2, 
1, 2; 1, 1, 1, 2, 3; −1, −2,
 −2, 0, 1]; rref (C)


1 0 0
4
7
4
7








y se obtiene 0 1 0 −5 −10 . De acuerdo al teorema anterior A−1 B = −5 −10.




0 0 1
3
6
3
6
Observación 1.2. Del Teorema 1.18 se sigue que al aplicar reducción Gauss-Jordan a una matriz invertible A
se obtiene I, si se aplican las mismas operaciones elementales que se aplicaron a A para reducirla a I entonces
se obtiene el producto de las correspondientes matrices elementales, producto que a su vez es igual a A−1 . Es
decir, si E1 , . . . , Ek son las matrices elementales asociadas a las operaciones elementales que se usaron para
reducir la matriz A, entonces al aplicar las mismas operaciones elementales y en el mismo orden sobre la matriz
I, el resultado final es A−1 .
Esto es cierto ya que aplicar una operación elemental a una matriz es equivalente a multiplicar por la matriz
elemental asociada a la operación a la izquierda, al comenzar con I obtenemos
E
E
E
k
2
1
· · · −−→
Ek · · · E1 = A−1 .
E1 I = E1 −−→
I −−→
Observación 1.3. Si en el Teorema 1.18 las columnas de la matriz B son los vectores B1 , . . . , Bq , entonces al
i h
i
h
aplicar reducción Gauss-Jordan a la matriz aumentada A B = A B1 · · · Bq obtenemos la matriz
h
i
A−1 B = A−1 B1 · · · A−1 Bq , obteniendo soluciones simultaneas a los sistemas Ax = B1 , . . . , Ax = Bq .
Ejemplo 1.33. Usar la observación anterior para resolver los sistemas
x2 + 2x3 = 2
x2 + 2x3 = 1
x1 + x2 + x3 = 2
−x1 − 2x2 − 2x3 = 0
y
x1 + x2 + x3 = 3
−x1 − 2x2 − 2x3 = 1.
Solución. Estos sistemas son equivalentes a las ecuaciones matriciales


 
 
0
1
2
1
2


 
 


 
 
′
Ax = b1 y Ax = b2 donde, A =  1
1
1  , b1 =  2  y b 1 =  3  .


 
 
−1 −2 −2
0
1
Estos se pueden resolver
simultaneamente calculando la forma escalonada
reducida de la

 matriz aumentada

4
7
1 0 0
0
1
2 1 2



i 
h




1
1 2 3  , la cual está dada por  0 1 0 −5 −10  (ver ejemplo anteA b 1 b2 =  1




3
6
−1 −2 −2 0 1
0 0 1
rior) y por tanto las respectivas soluciones a los sistemas están dadas por


 
7
4


 


 
y
x′ = −10 .
x = −5


 
6
3
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
35
Terminamos la sección con el siguiente teorema que será útil en el próximo capı́tulo, en este teorema se
explota el hecho de que las operaciones elementales son reversibles.
Teorema 1.19. Sea A una matriz de tamanõ m × n y A′ su forma escalonada reducida. Entonces Ax = 0 si
y sólo si A′ x = 0, es decir, x es una solución al sistema homogeneo Ax = 0 si y sólo si x es una solución al
sistema A′ x = 0.


a1n
a11 x1 + · · · + a1n xn = 0

.. 
..
, entonces el sistema es equivalente a
. 
.

· · · amn
am1 x1 + · · · + amn xn = 0,
h
i
el cual se puede resolver aplicando las operaciones elementales de fila a la matriz aumentada A 0 . Si aplicamos
h
i
operaciones hasta llegar a la forma escalonada reducida obtenemos la matriz A′ 0 , la cual nos da las soluciones
a11

 ..
Demostración. Si A =  .

am1
···
..
.
al sistema A′ x = 0. Ahora como las operaciones elementales son reversibles, comenzando con el sistema A′ x = 0,
podemos llegar al sistema Ax = 0. Por tanto Ax = 0 si y sólo si A′ x = 0.
Problemas
1.4.1. Determine si las siguientes

1


A = 1

4
matrices son invertibles y en caso afirmativo calcule su inversa.





2 0
4
2 0 4
1 1










2 2 , B = 0 2 2 y C = 0 2 −10 .





3 1
1
3 1 1
4 1
1.4.2. Escriba las siguientes matrices y sus

1


A = 1

4
1.4.3. Escribala
1


1
reducida. A = 

1

1
inversas como producto de matrices elementales.



2 0 4
1 1






y
B
=


0 2 2 .
2 2



3 1 1
4 1
matriz A como un producto de matrices elementales por una matriz en forma escalonada
1 1 1 1 1


1 1 1 1 2
.

1 1 1 2 3

1 1 2 3 4
1.4.4. si A y B tienen la misma forma escalonada reducida entonces existen matrices elementales E1 , . . . , Es
tal que A = E1 · · · Es B.
1.4.5. Sean A y B matrices de tamaños m × n y n × q respectivamente. Demuestre que rango(AB) ≤ rango(A)
(Ayuda: Use el Lema 1.9 y el Teorema 1.15)
36
1.5.
Inversas Laterales
En esta sección se definirá el concepto de inversa lateral, que generaliza el concepto de invertibilidad de
una matriz. Veremos que hay matrices que no son invertibles que tienen inversa a la izquierda o a la derecha y
mostraremos criterios claros que nos permitirán decidir cuando una matriz posee inversas laterales y algoritmos
para calcularlas. Terminaremos el capı́tulo con un teorema que reune todas las propiedades equivalentes a que
una matriz sea invertible.
Definición 1.14. Sea A una matriz de tamaño m × n.
1. Decimos que A tiene inversa a la izquierda si existe una matriz L de tamaño n × m tal que LA = In .
2. Decimos que A tiene inversa a la derecha si existe una matriz R de tamaño n × m tal que AR = Im .

1

yB=
0

0 1 1
0
es una inversa a la derecha de A y a la vez, A es

Ejemplo 1.34. Sean A = 
1
1 0

0



0, un fácil cálculo nos muestra que AB = I2 y por tanto B

1
una inversa a la izquierda de B. Nótese además que ni A ni
B son invertibles pues no son matrices cuadradas.
Tenemos el siguiente criterio para caracterizar las matrices que tienen inversa a la derecha. En lo que sigue,
para i = 1, . . . , n denotaremos por ei al vector columna en Rn cuya entrada es uno en la posición i y cero en
las demás entradas, es decir,
1
0
0
e1 =  ..  ,
.
0
0
0
1
0
e2 =  ..  ,
.
0
0
0
0
...
0
en =  ..  .
.
0
1
Teorema 1.20. Sea A una matriz de tamaño m × n, entonces las siguientes afirmaciones son equivalentes:
1. A tiene inversa a la derecha.
2. El sistema Ax = b tiene solución para cada b ∈ Rm .
3. rango(A) = m = número de filas de A.
4. La función TA : Rn −→ Rm definida por TA (x) = Ax es sobreyectiva.
Demostración. Vamos a demostrar que 1 ⇔ 2, 2 ⇔ 3 y 2 ⇔ 4.
h
i
“1 ⇒ 2”Si A tiene inversa a la derecha, existe R = R1 · · · Rm de tamaño n × m tal que AR = I. Sea
37
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
b = b1 e1 + · · · + bm em ∈ Rm entonces el vector c = b1 R1 + · · · + bm Rm es una solución al sistema Ax = b ya que
Ac = A(b1 R1 + · · · + bm Rm ) = b1 AR1 + · · · + bm ARm
 
b1
h
i 
 .. 
= AR1 · · · ARm  . 
 
bm
h
i
= A R1 · · · Rm b
{z
}
|
=R
= |{z}
AR b
=I
= b.
“2 ⇒ 1”Supongamos que la ecuación Ax = b tiene solución para cada b, entonces para cada i = 1, . . . , m, la
ecuación Ax = ei tiene solución. Sean r1 , . . . , rm las soluciones respectivas dichas ecuaciones. Es decir,
Ar1 = e1 , . . . , Arm = em .
h
Sea R = r1
···
i
rm , entonces se tiene que
h
AR = A r1
···
rm
i
Por tanto R es la inversa a la derecha de A.
"
Ar1
= |{z}
=e1
···
#
h
Arm =
e1
|{z}
=em
···
i
em = I m .
“2 ⇒ 3”Supongamos que Ax = b tiene solución para cada b y sabemos que rango(A) ≤ m = número de filas de
A. Si rango(A) < m, entonces las forma escalonada A′ de A tiene al menos una fila de ceros. Sean E1 , . . . , Ek
matrices elementales tal que A′ = E1 · · · Ek A y sea b = Ek−1 · · · E1−1 em entonces al aplicar reducción Gaussh
i
Jordan a la matriz A b usando las operaciones elementales de fila asociadas a las matrices E1 , . . . , Ek
#
"
i
h
E
·
·
·
E
b
E
·
·
·
E
A
1
k
1
k
obtenemos la matriz | {z } | {z } = A′ em . Como la última fila de A′ es de ceros, entonces
=A′
em
el sistema es inconsistente, es decir, para b = Ek−1 · · · E1−1 em , la ecuación Ax = b no tiene solución, lo que
contradice la hipótesis. Por tanto rango(A) = m.
“3 ⇒ 2”Si rango(A) = m = # de filas, entonces A′ tiene un pivote en cada fila, por tanto para todo b ∈ Rm
i
h
se tiene que la matriz A b no tiene pivote en la última columna y ası́ el sistema Ax = b siempre tiene al
menos una solución.
“2 ⇒ 4”Si la ecuación Ax = b tiene solución para todo b, entonces para todo b ∈ Rm , existe c ∈ Rn tal que
b = Ac = TA (c). Por tanto TA es sobre.
“4 ⇒ 2”Si TA es sobre, para todo b ∈ Rm , existe c ∈ Rn tal que b = TA (c) = Ac, es decir, x = c es una solución
al sistema Ax = b.
La parte 3. de este teorema nos dice que una matriz tiene inversa a la derecha si y sólo si su forma escalonada
reducida tiene un pivote en cada fila. El teorema también nos ofrece un método calcular la inversa a la derecha, el
38
cual está casi explı́cito en la demostración de 1 ⇒ 2, ya que en ese numeral se prueba que las columnas R1 , . . . , Rm
de la inversa a la derecha R son las respectivas soluciones a las ecuaciones Ax = e1 , Ax = e2 , . . . , Ax = en como
se ilustra en el siguiente ejemplo.
Procedimiento 1.1. Sea A una matriz de tamaño m × n y A′ la forma escalonada reducida de A, si A′ tiene
un pivote en cada fila entonces A tiene una inversa a la derecha, para calcularla hacemos lo siguiente:
1. Para i = 1, · · · , m, calculamos una solución ri al sistema Ax = ei , es decir, un vector ri tal que Ari = ei .
Sabemos que estos vectores existen por el Teorema 1.2.
h
2. Se hace R = r1
anterior.
···
i
rm la matriz cuyas columnas son los vectores r1 , · · · , rm calculados en el paso
De acuerdo al Teorema 1.20, la matriz R es una inversa a la derecha de A.


1 2 2
 tiene inversa a la derecha y en caso afirmativo
Ejemplo 1.35. Determine si la matriz A = 
−1 0 4
calcular una inversa a la derecha de A.


1
0
−4
 se tiene que rango(A) =
Solución. Como la forma escalonada de reducida de A es la matriz A′ = 
0 1
3
2 = número de filas, por tanto A tiene inversa a la derecha por el Teorema 1.20.
Para encontrar la inversa a la derecha de A debemos encontrar soluciones a las ecuaciones
 Ax = e1y Ax =
0
0
 
 
 1
1
e2 . Se puede verificar que soluciones particulares a estas ecuaciones están dadas por r1 =  2  y r2 = − 4  y
 
 
1
0
4
por tanto una inversa a la derecha de A está dada por


0
0

h
i 


R = r1 r2 =  12 − 14  .


1
0
4
El siguiente teorema carateriza las matrices con inversa a la izquierda, las propiedades son análogas a las del
teorema anterior para la inversa a derecha.
Teorema 1.21. Sea A una matriz de tamaño m × n, entonces las siguientes afirmaciones son equivalentes:
1. A tiene inversa a la izquierda.
2. El sistema Ax = b tiene a lo sumo una solución para cada b ∈ Rm .
3. La función TA : Rn −→ Rm definida por TA (x) = Ax es inyectiva.
4. El sistema Ax = θm tiene solución única.
5. rango(A) = n = número de columnas de A.
39
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Demostración. Para este teorema demostraremos las equivalencias en el orden 1 ⇒ 2, 2 ⇒ 3, 3 ⇒ 4, 4 ⇒ 5 y
5 ⇒ 1.
“1 ⇒ 2”Supongamos que A tiene inversa a la izquierda L , y sean v y w soluciones al sistema Ax = b. Entonces
b = |{z}
v = Iv = L |{z}
Av = L |{z}
LA w = Iw = w.
=Aw
=b
=I
Como v = w el sistema tiene a lo sumo una solución.
“2 ⇒ 3”Supongamos que Ax = b tiene a lo sumo una solución para todo b y que TA (v) = TA (w), entonces
Av = Aw. Sea b = Av, entonces la ecuación Ax = b tiene dos soluciones v y w, entonces v = w.
“3 ⇒ 4”Supongamos que TA es inyectiva. Entonces si v es tal que Av = θ se tiene que θ = Av = TA (v) y como
TA (θ) = Aθ = θ entonces TA (v) = TA (θ) y como TA es inyectiva, v = θ.
“4 ⇒ 5” Supongamos que el sistema Ax = θ tiene solución única, entonces por el Teorema 1.2 la forma
i h
i
h
escalonada reducida de la matriz A θ = A′ θ , donde A′ es la forma escalonada reducida de A tiene
un pivote en todas la columnas excepto la última, es decir, A′ tiene un pivote en cada columna y por tanto
rango(A) = n = número de columnas de A.
“5 ⇒ 1”Supongamos que rango(A) = n, entonces la forma escalonada A′ de A tiene un pivote en cada columna,
por tanto
··· 0 
0 1 ··· 0
1 0
 .. ..
. .
A′ = 
 00 00
. .
.. ..
. . .. 
. .
··· 1  .
··· 0 

. . ..
..
0 0 ··· 0
Sean E1 , . . . , Ek matrices elementales tal que A = E1 · · · Ek · A′ y sea
B = Ek−1 · · · E1−1 , entonces A′ = BA. Sean B 1 , . . . , B m
tenemos lo siguiente



B1A
B1




 . 
 . 
A′ = BA =  ..  A =  ..  .




BmA
Bm



B1


 . 
las filas de B, es decir B =  .. . Como A′ = BA


m
B


B1
 
 . 
Ahora tomemos C =  ..  la matriz formada con las primeras n filas de B, veamos
 
Bn
a la izquierda de A.



 
1 0 ···

B1A
B1



 
0 1 · · ·
 . 
 . 
CA =  ..  A =  ..  = primeras n filas de A′ = 
 .. .. . .


 
. .
.

n
n
B A
B
0 0 ···
que C es la matriz inversa
0



0

..  = I.
.

1
40
Este teorema también nos da una forma de determinar si una matriz tiene inversa a la izquierda (se calcula el
rango y la matriz tiene inversa a la izquierda si y sólo si el rango es igual al número de columnas). El teorema
también proveé un algorimo para calcular dicha matriz, el cual se describe a continuación.
Procedimiento 1.2. Sea A una matriz de tamaño m × n y sea A′ la forma escalonada de de A, si A′ tiene
un pivote en cada columna entonces A tiene una inversa a la izquierda. Si A tiene inversa a la izquierda esta
se puede calcular haciendo lo siguiente:
1. Se aplica reducción Gauss-Jordan a la matriz.
2. Se calcula el producto de las matrices elementales Ek · · · E1 asociadas a las operaciones elementales usadas
en el paso anterior. Este producto se puede calcular directamente aplicando sucesivamente las operaciones
elementales que se aplicaron en el paso anterior para reducir la matriz A comenzando con la matriz
identidad Im , con m = número de filas de A.
3. La matriz L formada por las primeras n filas de la matriz Ek · · · E1 es la inversa a la izquierda.
Ejemplo 1.36. (MatLab) Para cada una de las matrices abajo, determine si tienen inversa a la izquierda y
encuentrela en caso afirmativo.

Solución.
2


a. A = −4

−2
−1



2

1

b. B = 
1 −1
2 −1

0

1

1 −1


c. C = 0

2



1 .

1
1. Usando MatLab para calcular el rango de la matriz A obtenemos
>> A = [2, −1; −4, 2; −2, 1]; r = rank(A)
que r = 1, ası́ como rango(A) = 1 < número de columnas, entonces por el Teorema 1.21 la matriz no
tiene inversa a la izquierda.
2. La matriz B tiene 2 filas, de donde rango(B) ≤ 2 < 3 =número de columnas. Por tanto B no tiene
inversa a la izquierda.
3. El rango de esta matriz C es dos, entonces C tiene inversa a la izquierda. Para calcular una inversa a la
izquierda debemos aplicar el procedimiento descrito arriba,
1. Apliquemos reducción Gauss-Jordan a la matriz C



1 −1
1






0
0
1



2
1 −2F1 +F3 →F3 0
|
{z
}
E1





−1 F2 +F1 →F1 1 0
1 0










 0 1
 0 1 .
1





3
0 3 −3F2 +F3 →F3 0 0
|
| {z }
{z
}
E2
E3
41
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Donde E1 , E2 y E3 son las matrices elementales asociadas a cada una de las operaciones ejecutadas.
2. Aplicamos las operaciones efectuadas en la reducción a la matriz identidad 3 × 3. Esto es equivalente a
multiplicar las matrices elementales asociadas a las operaciones.





1 0 0 F2 +F1 →F1
1
1 0 0










 0 1 0
 0
0 1 0





−2
0 0 1 −2F1 +F3 →F3 −2 0 1
|
|
{z
}
E1
3. La matriz L = 
1 1
0 1
izquierda de C.
1
0
{z
E2 E1


1

0


0 = E3 E2 E1 .

1
1
1


 0
1

−3F2 +F3 →F3 −2 −3

0


0

1
}

0
, obtenida al suprimir la última fila a la matriz E3 E2 E1 , es una inversa a la
0
Hay otra forma de calcular la inversa a la izquierda de una matriz. Es fácil ver que si R es una inversa a la
derecha de At entonces L = Rt es una inversa a la izquierda de A. Esto se ilustra en el siguiente ejemplo.


1 −1




Ejemplo 1.37. (MatLab) Calcular una inversa a la izquierda de la matriz C = 0
1 .


2
1
Solución. Para calcular la inversa a la derecha de C t , necesitamos resolver las ecuaciones C t x = e1 y C t x = e2 .
Estas soluciones las calculamos con MatLab
>> C t =[1,0, 2; −1, 1,
 1]; e1 = [1; 0]; e2 = [0; 1]; r1 = A\e1, r2 = A\e2
1
−2
 3
3
 
 
r1 =  0  y r2 =  0  .
 
 
1
3
1
3

1
3

Entonces una inversa a la derecha de C t es la matriz R =  0


C es la matriz L = Rt = 
1
3
0
− 32
0

1
3
1
3
1
3
− 23



0 , por tanto una inversa a la izquierda de

1
3
.
De estos resultados obtenemos la siguiente caracterización para matrices invertibles.
Corolario 1.22. (Caracterización de una matriz invertible) Sea A una matriz cuadrada de tamaño n × n,
entonces las siguientes afirmaciones son equivalentes:
1. A es invertible.
2. A tiene inversa a la izquierda.
42
3. El sistema Ax = b tiene a lo sumo una solución para cada b ∈ Rn .
4. La función TA : Rn −→ Rn definida por TA (x) = Ax es inyectiva.
5. El sistema Ax = θn tiene solución única.
6. rango(A) = n = número de columnas de A = número de filas deA.
7. A tiene inversa a la derecha.
8. El sistema Ax = b tiene solución para cada b ∈ Rm .
9. La función TA : Rn −→ Rn definida por TA (x) = Ax es sobreyectiva.
10. La función TA : Rn −→ Rn definida por TA (x) = Ax es biyectiva.
11. At es invertible.
12. A es un producto de matrices elementales.
Demostración. Las condiciones 1. y 12. son equivalentes por el Teorema 1.17, las condiciones 1. y 11. son
equivalentes por el Teorema 1.11, las condiciones 2. a 6. son equivalentes por el Teorema 1.21 y las condiciones
6. a 10. son equivalentes por el Teorema 1.20. Es suficiente demostrar que 1 ⇔ 2.
“1⇒ 2”Si A es invertible, entonces A−1 A = I y por tanto A−1 es inversa a la izquierda de A.
“2⇒ 1”Si A tiene inversa a la izquierda, entonces existe B tal que BA = I y por el Teorema 1.21, rango(A) = n =
número de columnas. Como A es cuadrada entonces el número de filas es igual al número de columnas e igual
al rango(A), entonces por el Teorema 1.20, A tiene una inversa a la derecha C, de donde AC = I, entonces se
tiene que
B = BI = B(AC) = (BA)C = IC = C.
Entonces BA = AB = I y por tanto A es invertible y B = A−1 .
Problemas
1.5.1. Determine cual de las matrices tiene inversa a la izquierda o a la derecha y compute una para las que la
tengan:
a.

1

2
1 1
2 2

.
b.


2 −1
3
4

5
.
1
c.

1


4

2

2


8 .

4
d.

1


1

1

1


2 .

4
43
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

1.5.2. Encuentre soluciones a las ecuaciones Ax = e1 y Ax = e2 con A = 
una inversa a la derecha de la matriz A.

1
1 1
1
3 1
4
1 2

 y úselas para calcular





 1 1 2
.
1.5.3. Calcule una inversa a la izquierda de la matriz A = 


 1 2 3


1 2 4


1 1 1 1 1 1




1 1 1 1 1 2
 de dos formas: primero usando
1.5.4. Calcule una inversa a la derecha de la matriz B = 


1 1 1 1 2 3


1 1 1 2 3 4
el Procedimiento 1.1 y después usando el Procedimiento 1.2 para calcular una inversa a la izquierda de B t .
1.5.5. Demuestre que si una matriz A de tamaño m × n tiene inversa a la izquierda L e inversa a la derecha
R, entonces L = R y m = n.
1.5.6. Demuestre que L es una inversa a la izquierda de A si y sólo si Lt es in inversa a la derecha de At .
Concluya que si rango(A) = número de columnas de A, entonces rango(At ) = rango(A).
1.5.7. Si A es 4 × 3 y B es 3 × 4 muestre que AB no es invertibe. (Ayuda: Muestre que la ecuación Bx = 0
tiene una solución no trivial.)
1.5.8. Gerenalizando el problema anterior, si A es n × m y B es m × n con m < n muestre que AB no es
invertible.
1.5.9. Muestre que una matriz no cuadrada no puede tener inversa a la izquierda y a la derecha.
1.5.10. Muestre que una matriz no cuadrada no puede ser la inversa a la izquierda y a la derecha de otra
matriz.
1.5.11. Muestre que Ax = b tiene solución para todo b si y sólo si At y = 0 tiene solución única.
1.5.12. Muestre que las matrices inversas a izquierda o derecha de una matriz no cuadrada no son únicas, de
hecho, pueden existir infinitas.
El siguiente ejercicio tiene el propósito de mostrar que en la definición de matrices cuadradas invertibles es
suficiente exigir que existe B tal que AB = I.
1.5.13. Sea A ∈ Mn (R) una matriz y suponga que existe B tal que AB = I. Demuestre lo siguiente:
1. rangoA = n.
2. existe C tal que CA = I.
44
3. C = B
4. A es invertible.
Capı́tulo 2
Espacios Vectoriales
2.1.
Definición y Ejemplos
En el capı́tulo anterior se dieron ejemplos, sin mencionarlo, de espacios vectoriales. Más concretamente en los
Teorema 1.5 y 1.6 se mostró que el conjunto de matrices de tamaño m × n y el conjunto de vectores columna
Rn son espacios vectoriales. Solo nos falta enunciar la definición y ver que estos conjuntos la satisfacen. En
este capı́tulo solo trabajaremos sobre Rn y los teoremas serán acerca de este conjunto, en el Capı́tulo 3 se
demostrarán los teoremas generales.
Definición 2.1. Sea V un conjunto no vacio con dos operaciones + : V × V → V y · : R × V → V , decimos
que V es un espacio vectorial sobre R si para todo x, y y z ∈ V y para todo α y β ∈ R se cumple lo siguiente:
1. (x + y) + z = x + (y + z),
2. existe θ ∈ V tal que θ + x = x + θ = x, (A θ se le llama el neutro de V )
3. existe w tal que x + w = w + x = θ, (A w se le llama el inverso aditivo de x)
4. x + y = y + x,
5. α · (x + y) = α · x + α · y,
6. (α + β) · x = αx + β · x,
7. α · (β · x) = (αβ) · x,
8. 1 · x = x.
Ejemplo 2.1.
1. El conjunto de vectores en Rm es un espacio vectorial, por el Teorema 1.6.
2. El conjunto de matrices m × n es un espacio vectorial, esto por el Teorema 1.5. A este conjunto lo denotaremos por Mmn (R) cuando las entradas sean reales y por Mmn (C) cuando las entradas sean complejas.
En el caso en que m = n, usaremos la notación Mn (R) o Mn (C).
3. Sea Pn = {a0 + a1 t + · · · + an tn | a0 , . . . , an ∈ R} el conjunto de polinomios de grado a lo sumo n en la
indeterminada t, este conjunto es un espacio vectorial sobre R bajo las operaciones:
45
46
a0 + a1 t + · · · + an tn + b0 + b1 t + · · · + bn tn = (a0 + b0 ) + (a1 + b1 )t + · · · + (an + bn )tn y
α · (a0 + a1 t + · · · + an tn ) = α · a0 + α · a1 t + · · · + α · an tn .
Veamos que estas operaciones satisfacen todas las propiedades de la
definición de espacio vectorial.
Sean p1 = a0 + a1 t + · · · + an tn , p2 = b1 t + · · · + bn tn y p3 = c0 + c1 t + · · · + cn tn ∈ Pn , α, β ∈ R,
1.
(p1 + p2 ) + p3 =(a0 + a1 t + · · · + an tn + b0 + b1 t + · · · + bn tn )
+ c 0 + c 1 t + · · · + c n tn
=(a0 + b0 ) + (a1 + b1 )t + · · · + (an + bn )tn
+ c 0 + c 1 t + · · · + c n tn
(definición de suma en Pn )
=((a0 + b0 ) + c0 ) + ((a1 + b1 ) + c1 )t + . . .
· · · + ((an + bn ) + cn )tn
(definición de suma en Pn )
=(a0 + (b0 + c0 )) + (a1 + (b1 + c1 ))t + . . .
· · · + (an + (bn + cn ))tn
(asociatividad en R)
=a0 + a1 t + · · · + an tn + (b0 + c0 ) + (b1 + c1 )t + . . .
· · · + (bn + cn )tn
(definición de suma en Pn )
=a0 + a1 t + · · · + an tn
+ (b0 + b1 t + · · · + bn tn + c0 + c1 t + · · · + cn tn )
(definición de suma en Pn )
=p1 + (p2 + p3 )
2. Sea θ = 0 el polinomio constante = 0, entonces
p1 + θ = a 0 + a 1 t + · · · + a n t n + 0 = a 0 + a 1 t + · · · + a n t n = p1
3. Sea w = −a0 − a1 t + · · · − an tn entonces
w + p1 = −a0 − a1 t + · · · − an tn + a0 + a1 t + · · · + an tn +
= (−a0 + a0 ) + (−a1 + a1 )t + · · · + (−an + an )tn
= 0 = θ.
47
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
4.
p 1 + p 2 = a 0 + a 1 t + · · · + a n t n + b0 + b1 t + · · · + bn t n
= (a0 + b0 ) + (a1 + b1 )t + · · · + (an + bn )tn
(Definición de suma en Pn )
= (b0 + a0 ) + (b1 + a1 )t + · · · + (bn + an )tn
(Conmuatitividad en R)
= b0 + b1 t + · · · + bn t n + a 0 + a 1 t + · · · + a n t n
(Definición de suma en Pn )
= p2 + p1
5.
α · (p1 + p2 ) = α · (a0 + a1 t + · · · + an tn + b0 + b1 t + · · · + bn tn )
= α · ((a0 + b0 ) + (a1 + b1 )t + · · · + (an + bn )tn )
definición de suma en Pn
= α(a0 + b0 ) + α(a1 + b1 )t + · · · + α(an + bn )tn
definición de producto por escalar en Pn
= (αa0 + αb0 ) + (αa1 + αb1 )t + · · · + (αan + αbn )tn
distributividad en R
= αa0 + αa1 t + · · · + αan tn + αb0 + αb1 t + · · · + αbn tn
definición de suma en Pn
= α · (a0 + a1 t + · · · + an tn ) + α · (b0 + b1 t + · · · + bn tn )
definición de producto por escalar en Pn
= α · p1 + α · p2
48
6.
(α + β) · p1 = (α + β) · (a0 + a1 t + · · · + an tn )
= (α + β)a0 + (α + β)a1 t + · · · + (α + β)an tn
definición de producto por escalar en Pn
= (αa0 + βa0 ) + (αa1 + βa1 )t + · · · + (αan + βan )tn
ditributividad en R
= αa0 + αa1 t + · · · + αan tn + βa0 + βa1 t + · · · + βan tn
definición de suma en Pn
= α · (a0 + a1 t + · · · + an tn ) + β · (a0 + a1 t + · · · + an tn )
definición de producto por escalar en Pn
= α · p1 + β · p1
7.
(αβ) · p1 = (αβ) · (a0 + a1 t + · · · + an tn )
= (αβ)a0 + (αβ)a1 t + · · · + (αβ)an tn
definición de producto por escalar en Pn
= α(βa0 ) + α(βa1 )t + · · · + α(βan )tn
asociatividad en R
= α · (βa0 + βa1 t + · · · + βan tn )
definición de producto por escalar en Pn
= α · (β · (a0 + a1 t + · · · + an tn ))
definición de producto por escalar en Pn
= α · (β · p1 )
8.
1 · p1 = 1 · (a0 + a1 t + · · · + an tn ) = 1 · a0 + 1 · a1 t + · · · + 1 · an tn
= a 0 + a 1 t + · · · + a n tn
= p1 .
4. El conjunto de polinomios con entradas en R,
R[t] = {a0 + a1 t + · · · + an tn | a0 , . . . , an ∈ R, n ∈ N ∪ {0}} ,
es un espacio vectorial.
49
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
5. Si X es un conjunto, el conjunto de funciones de X en R,
F(X, R) = {f : X −→ R | f es una función },
es un espacio vectorial sobre R con las operaciones de suma y producto por escalar definidos por:
(f + g)(x) = f (x) + g(x)
y
(αf )(x) = αf (x).
Los detalles se dejan como ejeercicio al lector.
Los espacios vectoriales satisfacen las siguientes propiedades que se desprenden de la definición.
Teorema 2.1. Sea V un espacio vectorial, x ∈ V y α ∈ R entonces
1. El neutro es único, es decir, si θ y θ′ son neutros entonces θ = θ′ ,
2. el inverso aditivo de x es único, es decir, si w y w′ son inversos aditivos de x entonces w = w′ , (dada la
unicidad del inverso aditivo de x, este será denotado por −x)
3. α · θ = θ,
4. 0 · x = θ,
5. −1 · x = −x,
Demostración.
6. Si α · x = θ entonces α = 0 o x = θ.
1. θ = θ + θ′ = θ′ + θ = θ′ .
2. w = w + θ = w + (x + w′ ) = (w + x) + w′ = θ + w′ = w′ .
3. αθ + αθ = α(θ + θ) = αθ, sumando el inverso aditivo de αθ a ambos lados tenemos: αθ = θ.
4. 0x = (0 + 0)x = 0x + 0x, sumando el inverso aditivo de 0x a ambos lados tenemos que θ = 0x.
5. −1x + x = −1x + 1x = (−1 + 1)x = 0x = θ. como el inverso aditivo de x es único, tenemos que −1x = −x.
6. Supongamos que αx = θ y que α 6= 0. Si multiplicamos a ambos lados por
1
1
(αx) = θ
α
|α {z }
|{z}



=



⇒
1x = θ
|{z}
=x
=θ
1 

α
x
α
|{z}
⇒
1
tenemos que
α
x=θ
=1
Problemas
2.1.1. Demuestre que R+ = {x ∈ R | x > 0} es un espacio vectorial bajo las operaciones
x ⊕ y = xy
para todo x, y ∈ R+ y todo α ∈ R.
y
α • x = xα ,
50
2.1.2. Generalizando el problema anterior, demuestre que el conjunto
n
(R+ ) = {(x1 , . . . , xn ) | x1 , . . . , xn ∈ R+ } es un espacio vectorial bajo las operaciones
(x1 , . . . , xn ) ⊕ (y1 , . . . , yn ) = (x1 y1 , . . . , xn yn )
y
α
α • (x1 , . . . , xn ) = (xα
1 , . . . , xn ).
2.1.3. Determine cuales de los siguientes conjuntos son espacios vectoriales con las operaciones indicadas. Si
no lo son, enuncie las propiedades que no cumplen.
1. El conjunto de matrices simétricas, {A ∈ Mn (R) | At = A}, bajo la suma y el producto por escalar usual de
matrices. (La suma y producto usual de matrices se dieron en la Definición ??.)
2. El conjunto de matrices anti-simétricas, {A ∈ Mn (R) | At = −A}, bajo la suma y el producto por escalar
usual de matrices.

 

 x 3. El conjunto R+ × R =   x, y ∈ R, x > 0 bajo la suma y el producto por escalar usual de R2 . (La suma

 y
y producto usual de vectores en Rn se dieron en la Definición ??.)

 

 x 4. El conjunto (R \ R+ ) × (R \ R+ ) =   x, y ∈ R, x, y < 0 bajo la suma y el producto por escalar usual

 y
de R2 .
5. El conjunto
R+ × R+ ∪ R \ R+ × R \ R+ = (x, y) ∈ R2 | x, y ≥ 0
bajo la suma y producto por escalar usuales de R2 .
o
x, y ≤ 0







x


 



6. El conjunto  y  x, y ∈ R, x > 0 bajo la suma y el producto por escalar usual de R3 .








 x−y

7. El conjunto {a + at2 + · · · + at2n | a ∈ R} bajo las operaciones de suma y producto por escalar usual de
polinomios. (Ver Ejemplo 2.1 ı́tem 3.)

 a
8. El conjunto 
 a


1
 a ∈ R bajo las operaciones usuales para matrices.

a

9. El conjunto {a0 + a1 t + · · · + an tn | a0 = 1} bajo las operaciones de suma y producto por escalar usual de
polinomios.
2.1.4. Demuestre que R × R \ {0} es un espacio vectorial con las operaciones (a1 , a2 ) + (b1 , b2 ) = (a1 + b1 , a2 b2 )
y α(a, b) = (αa, bα ).
51
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO




 1 a  a ∈ R es un espacio vectorial bajo la suma definida por
2.1.5. Demuestre que el conjunto V = 

 0 1
A ⊕ B = AB donde AB denota el producto usual de matrices y el producto por escalar definido por

 

1 αa
1 a
.
=
α·
0 1
0 1
2.1.6. Demuestre que un plano que pasa por el origen,
S = (x, y, z) ∈ R3 | αx + βy + γz = 0,
α, β, γ ∈ R ,
es un espacio vectorial bajo la suma y producto por escalar usuales de R3 .
2.1.7. Generalizando el problema anterior, demuestre que un hiperplano que pasa por el origen,
S = {(x1 , . . . , xn ) ∈ Rn | α1 x1 + · · · + αn xn = 0,
α1 , . . . , αn ∈ R} ,
es un espacio vectorial bajo la suma y producto por escalar usuales de Rn .
2.1.8. Generalizando aún más el Problema 2.1.6, demuestre que el conjunto de soluciones a un sistema homogéneo,
S=





α11 x1 + · · · + α1n xn = 0
..
,
.
(x1 , . . . , xn ) ∈ Rn 



αn1 x1 + · · · + αnn xn = 0
αij ∈ R, para i, j = 1, . . . , n.
es un espacio vectorial bajo la suma y producto por escalar usuales de Rn .





,




Ayuda: Recuerde
al sistema
de ecuaciones son las soluciones a la ecuación matricial


 que las soluciones
x1
α11 · · · α1n
 


.


 ..
..
..  y x =  ... 
Ax = 0 con A =  .
.
.
 


xn
αn1 · · · αnn
2.1.9. Demuestre que los conjuntos dados en los numerales 4. y 5. del Ejemplo 2.1 son espacios vectoriales con
las operaciones indicadas.
2.1.10. Sea V un espacio vectorial y sean x, y ∈ V , para cada una de las siguientes ecuaciones, demuestre que
existe un único z ∈ V que la satisface
1.
2.2.
x + z = y.
2.
x − z = y.
3.
αz = x.
4.
x + αz = y.
Subespacios
En esta sección se dará un criterio para determinar si un subconjunto de un espacio vectorial es un subespacio
y como construir nuevos subespacios de otros.
52
Definición 2.2. Sea V un espacio vectorial y φ 6= W ⊆ V , decimos que W es un subespacio de V si W es
también un espacio vectorial bajo las mismas operaciones de suma y producto por escalar de V .
Ejemplo 2.2.
1. En el Ejemplo 2.1 vimos que Pn es un espacio vectorial para todo n, como Pn−1 ⊆ Pn y
ambos son espacios vectoriales, tenemos que Pn−1 es un subespacio de Pn .
2. También tenemos que Pn es un subespacio de R[t] para todo n, al ser un espacio vectorial y subconjunto
de R[t].
3. El conjunto de números reales R es un espacio vectorial, el conjunto de números complejos C también es
un espacio vectorial, como R ⊆ C tenemos que R es un subespacio de C.
En teorı́a para demostrar que un subconjunto no vacio de un espacio vectorial V es un subespacio es necesario
determinar si cumple las ocho condiciones de la definición, sin embargo, el siguiente teorema nos da un criterio
en el que solo es necesario mostrar que este es cerrado bajo la suma y el producto por escalar.
Teorema 2.2. Sea V un espacio vectorial y φ 6= W ⊆ V , entonces W es un subespacio de V si para todo
w, w′ ∈ W y para todo α ∈ R se satisface que
1.
w + w′ ∈ W,
2.
αw ∈ W.
Demostración. Debemos demostrar W cumple las ocho condiciones de espacio vectorial.
1. La asociatividad se cumple para todo v, v ′ y v ′′ ∈ V , entoncs en particular si estos están en W .
2. Como W 6= φ, existe w ∈ W , entonces por hipótesis tenemos que −w = (−1)w ∈ W , en consecuencia
0 = −w + w ∈ W .
3. Si w ∈ W entonces por la hipótesis 2. tenemos que −w = (−1)w ∈ W .
4-8. Estas propiedades se cumplen para todo w, w′ ∈ V , en particular si w, w′ ∈ W .
Por tanto W es un espacio vectorial y como W ⊆ V , tenemos que W es un subespacio de V .

 


x


1

  

 ..  Ejemplo 2.3. Sea H =  .  xn = 0 ⊆ Rm , demuestre que H es un subespacio de Rm .


 





 x
n
Solución. Primeronótese
 H 6= φ ya que θn ∈ H, veamos que H satisface las condiciones 1. y 2. del
  que
y1
x1
   
 ..   .. 
Teorema 2.2. Sean  .  ,  .  ∈ H y α ∈ R, entonces xn = 0 = yn por tanto
   
yn
xn
    
 

 
  

x1
y1
x 1 + y1
x 1 + y1
x1
x1
αx1
    
 

 
  

..
 ..   ..  
  .. 
 .. 
 ..   .. 
=
∈
H
y
α
=
α
=
 . + . =








 ∈ H.
.
    
  . 
 . 
.  . 
xn
yn
x n + yn
0
xn
0
0
53
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
El Teorema 2.2 no solo facilita la verificación de si un subconjunto es un subespacio, también facilita las
demostraciones de los siguientes teoremas.
Teorema 2.3. Sea V un espacio vectorial y sean W1 y W2 subespacios de V entonces W1 ∩ W2 es un subespacio
de V .
Demostración. Como W1 y W2 son subespacios, entonces 0 ∈ W1 y 0 ∈ W2 , se sigue que 0 ∈ W1 ∩ W2 y por
tanto W1 ∩ W2 6= φ. Ahora mostremos que el conjunto W1 ∩ W2 satisface las condiciones 1. y 2. del Teorema
2.2.
Sean w, w′ ∈ W1 ∩ W2 , entonces w, w′ ∈ W1 y w, w′ ∈ W2 , luego w + w′ ∈ W1 y w + w′ ∈ W2 , por tanto
w + w′ ∈ W1 ∩ W2 .
Sea α ∈ R, como W1 y W2 son subespacios tenemos que αw ∈ W1 y αw ∈ W2 , por tanto αw ∈ W1 ∩ W2 .
Concluimos que W1 ∩ W2 es un subespacio de V .
Teorema 2.4. Sea V un espacio vectorial y sean W1 y W2 subespacios de V y definamos
W1 + W2 = {w1 + w2 | w1 ∈ W1 y w2 ∈ W2 }
entonces W1 + W2 es un subespacio de V .
Demostración. Esta se deja como ejercicio.
Problemas

 a
2.2.1. Sea V = M2 (R), demuestre que H1 = 
 0
pacios de V y describa el conjunto H1 ∩ H2 .



 a

b  a, b, c ∈ R y H2 = 
 b

c



b  a, b ∈ R son subes

−a
2.2.2. Demuestre el Teorema 2.4
 



x


1


  
.


n
.
2.2.3. Demuestre que un hiperplano H de R , H =  .  α1 x1 + · · · + αn xn = 0, α1 , . . . , αn ∈ R es un


 




 x

n
subespacio de Rn .
2.2.4. Sea A una matriz m × n, demuestre que el conjunto H = {x ∈ Rn | Ax = 0} es un subespacio de Rn .
(Este ejercicio es una generalización del ejercicio anterior, nótese que en el ejercicio anterior la matriz A es la
matriz A = [α1
···
αn ]. )
2.2.5. La traza de una matriz A = (aij ) ∈ Mn (R) se define como tr(A) = a11 + · · · + ann . Demuestre que
el conjunto de matrices de traza cero es un subespacio de Mn (R), a este subespacio se le denota por sln (R) o
sl(n, R).
54
2.2.6. Sean A, B ∈ Mn (R) y α, β ∈ R, demuestre que
1. tr(αA + βB) = αtr(A) + βtr(B),
2. tr(AB) = tr(BA)
3. tr(At ) = tr(A).
2.2.7. De ejemplos de subconjuntos de R2 que cumplan lo siguiente:
1. que sea cerrado bajo el producto por escalar pero no que sea cerrado bajo la suma,
2. que sea cerrado bajo la suma pero que no sea cerrado bajo el producto por escalar.
2.2.8. Demuestre que el conjunto solución de el sistema homogéneo
a11 x1 + · · · + a1n xn = 0
..
.
am1 x1 + · · · + amn xn = 0
n
es un subespacio de R
.
 

x1
a11 · · · a1n
 


.. 
 . 
 .
..
la matriz del sistema, demuestre que x =  ..  es una solución al
Ayuda: Sea A =  ..
.
. 
 


xn
am1 · · · amn
sistema si y sólo si Ax = 0 y use el Ejercicio 2.2.4.
2.2.9.
1. Construya un contraejemplo que muestre que la unión de subespacios no es un
subespacio.
2. Sea V un espacio vectorial y W1 y W2 subespacios de V , demuestre que W1 ∪ W2 es un subespacio si y
sólo si W1 ⊆ W2 o W2 ⊆ W1 .
2.2.10. Sea V un espacio vectorial y sean W1 y W2 subespacios de V , demuestre que W1 + W2 es el subespacio
más pequeño que contiene a W1 y a W2 .
2.2.11. Demuestre que el conjunto de matrices simétricas,
Sn = {A ∈ Mn (R) | A es simétrica },
es un subespacio de Mn (R).
2.2.12. Demuestre que el conjunto de matrices antisimétricas,
An = {A ∈ Mn (R) | A es antisimétrica },
es un subespacio de Mn (R).
55
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
2.2.13. Una función se llama par si f (−x) = f (x), para todo x. Demuestre que el conjunto de funciones pares
es un subespacio vectorial de F(R, R).
Demuestre también que el subconjuto formado por las funciones impares, funciones tal que f (−x) = −f (x),
para todo x, también es un subespacio de F(R, R).
2.2.14. Sea F = F([0, 1], R), el conjunto de funciones del intervalo [0, 1] en R, demuestre que los siguientes
subconjuntos son subespacios de F:
1. el conjunto C([0, 1], R) de funciones continuas del intervalo [0, 1] en R,
Z 1
f (x)dx = 0 .
2. el conjunto f ∈ F 0
2.2.15. Sea V un espacio vectorial y sean H1 y H2 subespacios, demuestre que H1 ∩ H2 es el subespacio más
grande contenido en H1 y H2 .
2.2.16. Sea V = {f : R −→ R | f es una función } el espacio de funciones de R en R. Determine si los
siguientes conjuntos son subespacios de V .
1. H1 = f ∈ V lı́m− f (x) = +∞ .
x→0
2.
H2 =
f ∈V
lı́m f (x) = 0 .
x→−∞
2.2.17. Sean H, K y L subespacios de un espacio vectorial V . Haga lo siguiente
1. Muestre que (H ∩ K) + (H ∩ L) ⊆ H ∩ (K + L).
2. Exhiba un contraejemplo que muestre que la igualdad H ∩ (K + L) = (H ∩ K) + (H ∩ L) no es cierta.
3. Muestre que si K ⊆ H entonces H ∩ (K + L) = K + (H ∩ L).
4. Muestre que H + (K ∩ L) ⊆ (H + K) ∩ (H + L).
5. Exhiba un contraejemplo que muestre que la igualdad H + (K ∩ L) = (H + K) ∩ (H + L) no es cierta.
2.2.18. Si A ⊆ V es un subconjunto de un espacio vectorial V , definimos L(A) como el conjunto L(A)=intersección
de subespacios que contienen a A, muestre lo siguiente:
1. L({x}) = {ax : a ∈ R}
2. H es un subespacio de V si y sólo si L(W ) = W .
3. Si A ⊆ B entonces L(A) ⊆ L(B).
4. Si H1 y H2 son subespacios entonces L(H1 ∪ H2 ) = H1 + H2 .
5. L(A) es el subespacio más pequeño que contiene a A.
2.2.19. Muestre que {p ∈ R4 [t] |
R1
0
p(x)dx = 0} es un subespacio .
56
2.3.
Independencia Lineal
En esta sección se estudiará el concepto de independencia lineal el cual nos permitirá determinar cuando
un vector en un conjunto dado de vectores se puede expresar en términos de los demás. También se dará un
criterio que nos permitirá determinar computacionalmente cuando un conjunto de vectores en Rm es linealmente
independiente. Se usará muy a menudo la frase combinación lineal, la cual definimos a continuación.
Definición 2.3. Sea V un espacio vectorial y sean v1 , . . . , vk ∈ V , una combinación lineal de estos vectores es
una expresión de la forma
α1 v 1 + · · · + αk v k ,
donde α1 , . . . , αk son reales.
Definición 2.4. Sea V un espacio vectorial y sean v1 , . . . , vk ∈ V , decimos que el conjunto {v1 , . . . , vk } es
linealmente independiente si la única combinación lineal de los vectores v1 , . . . , vk que produce el vector nulo es
la trivial, es decir, si se tiene que α1 v1 + · · · + αk vk = 0 entonces α1 = α2 = · · · = αk = 0. En este caso también
diremos que los vectores v1 , . . . , vk son linealmente independientes o simplemente LI para simplificar.
Si el conjunto {v1 , . . . , vk } no es linealmente independiente, decimos que es linealmente dependiente o simplemente LD para simplificar.
Observación 2.1. De la definición anterior se deprende que si el conjunto {v1 , . . . , vk } es LD si existe una
combinación lineal de los vectores v1 , . . . , vk que se anula, es decir, {v1 , . . . , vk } es LD si y sólo si existen
constantes α1 , . . . , αk , no todas cero, talque
α1 v1 + · · · + αk vk = 0.
(2.1)
Lo que es equivalente a decir que alguno de los vi se puede escribir como una combinación lineal de los demas,
esto ya que al menos uno de los αi 6= 0, por tanto despejando por vi en (2.1) tenemos
vi =
−α1
αi−1
αi+1
αk
v1 − · · · −
vi−1 −
vi+1 − · · · −
vk .
αi
αi
αi
αi
Es decir, un conjunto es LD si y sólo si uno de los vectores es una combinación lineal de los demás.
 
 
 
0
0
1
Ejemplo 2.4. Los vectores v1 =   y v2 =   son LI ya que si suponemos que α1 v1 + α2 v2 =   tenemos
0
1
0
que
 
 

0
 = α1 v 1 + α2 v 2 =  
0
α2
α1
lo que implica que α1 = 
α2 = 0.  
2
1
Los vectores v1 =   y v2 =   son LD ya que v2 = 2v1 lo que es equivalente a escribir −2v1 + v2 = 0 y
2
1
por la definición se sigue que v1 y v2 son LD.
57
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
De la última observación obtenemos una interpretación geométrica que podemos usar para conjuntos pequeños
de vectores la cual exhibimos a continuación.
El conjunto de vectores {v, w} es LD si y sólo si w = αv, es decir, el conjunto {v, w} es LD si y sólo si w
es un múltiplo de v. La siguiente figura nos muestra las posibilidades y aunque se usa una gráfica en R2 , vale
la pena aclarar que la mismos casos se cumplen para un par de vectores en dimensiones mayores.
w
w
v
v
Vectores LD
Vectores LI
Un conjunto formado por tres vectores {v, w, z} es LD si y sólo si uno de ellos es combinación lineal de los
otros. Esta última propiedad nos lleva a dos casos:
Caso 1: Dos vectores, digamos w y z, son ambos múltiplos de v. En este caso los tres vectores están contenidos
en una lı́nea.
Caso 2: Un vector, digamos z, es combinación lineal de v y w, pero v no es múltiplo de w. En este caso
tenemos que z es de la forma z = αv + βw y como la suma de dos vectores se rige por la ley del paralelogramo,
esta última ecuación implica que z está contenido en el mismo plano que contiene a v y w.
Concluimos que tres vectores son LD si y sólo si estos están contenidos en una lı́nea o en un plano.
En consecuencia tenemos que tres o más vectores en R2 son necesariamente LD. La siguiente figura nos
muestra los posibles casos geométricos de tres vectores
z
v
z
w
b
z
b
w
b
v
Vectores LD
Vectores LD
Vectores LI
Del Teorema 2.5 se deduce facilmente que cuatro o más vectores en R3 son LD, por tanto, para exhibir
geométricamente cuatro vectores LI se necesitan al menos 4 dimensiones y por este motivo no podemos exhibir
más figuras en las que se consideren cuatro o más vectores LI.

 
 
 



−1 
2
1



 
 
 
 
 
 
Ejemplo 2.5. 1. El conjunto v1 = −1 , v2 = 3 , v3 = −9 es LD ya que v3 = 3v1 − 2v2 de donde

 
 
 





6 
0
2
3v1 − 2v2 − v3 = 0.
58
 
 
 

1 
0
1

 
 
 
 
 
 
2. El conjunto de vectores v1 = 1 , v2 = 1 , v3 = 0 es LI ya que si existieran constantes α1 , α2 , α3

 
 
 





1 
1
0
tal que α1 v1 + α2 v2 + α3 v3 = 0 entonces tendrı́amos que
 
 
 
 
1
0
1
0
 
 
 
 
 
 
 
 
0 = α1 v1 + α2 v2 + α3 v3 = α1 1 + α2 1 + α3 0
 
 
 
 
1
1
0
0
      

α
0
α
α + α3
 1    3  1

      

= α1  + α2  +  0  = α1 + α2 
      

0
α2
α3
α2 + α3





α1 + α3 = 0
De donde α1 + α2 = 0, el cual es equivalente a la ecuación matricial
α2 + α3 = 0

1 0


1 1

0 1

   
0
1
α
  1  
   
0 α2  = 0 .
   
0
1
α3
(2.2)

1




Al aplicar reducción Gauss-Jordan a la matriz 1 1 0 obtenemos la matriz identidad, luego la única solución


0 1 1
al sistema (2.2) es la trivial, α1 = 0, α2 = 0 y α3 = 0. Por tanto el conjunto {v1 , v2 , v3 } es LI.
1 0
En Rm es fácil establecer un criterio para determinar si un conjunto de vectores es LI o no. De la definición se
sigue que un conjunto de vectores {v1 , . . . , vk } ⊆ Rm es LD si existen constantes α1 , . . . , αk , no todas cero tal
que α1 v1 + · · · + αk vk = 0 pero esta ecuación la podemos escribir matricialmente de la siguiente forma
 
α1
i 
h
 .. 
0 = α1 v 1 + · · · + αk v k = v 1 · · · v k  .  .
 
αk
  
0
α1
h
i   
.
  .
De esto se sigue que los vectores son LD si la ecuación α1 v1 + · · · + αk vk = v1 · · · vk  ..  =  ..  tiene
   
0
αk
soluciones no triviales lo cual, por el Teorema 1.21, es equivalente a que el rango de A es igual al número de

sus columnas. Este criterio lo enunciamos a continuación en le siguiente teorema.
h
i
Teorema 2.5. Sea {v1 , . . . , vk } ⊆ Rm y sea A = v1 · · · vk la matriz cuyas columnas son los vectores
v1 , . . . , vk , entonces el conjunto {v1 , . . . , vk } es LI si y sólo si rangoA = k = # de columnas de A.
59
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Demostración. El conjunto {v1 , . . . , vk } es LI si y sólo si las únicas constantes α1 , . . . , αk tal que α1 v1 + · · · +
   
α1
0
h
i   
 ..   .. 
αk vk = 0 son α1 = · · · = αk = 0 si y sólo si la única solución al sistema v1 · · · vk  .  =  .  es el vector
{z
}   
|
=A
αk
0
   
0
α1
   
 ..   .. 
 .  =  .  y por el Teorema 1.21 esto es equivalente a que rangoA = k = # de columnas de A.
   
0
αk
En este capı́tulo nos concentraremos en estudiar criterios que aplican solo para vectores en Rm , pero estos
serán generalizados a espacios vectoriales arbitrarios de dimensión finita en la Capı́tulo 3 usando los teoremas
de isomorfismo.
Del teorema se deduce el siguiente procedimiento computacional para determinar si un conjunto de vectores
es LI y si no lo son, también nos permite encontrar la dependencia lineal entre los vectores, el procedimiento se
enuncia a continuación.
Procedimiento 2.1. (Procedimiento para determinar si un conjunto de vectores de Rm es linealmente independiente.) Sea {v1 , . . . , vk } un conjunto de vectores en Rm , para determinar si este conjunto es
LI hacemos lo siguiente:
h
1. Aplicamos reducción Gauss-Jordan a la matriz A = v1
···
i
vk .
2. Si la forma escalonada reducida A′ de A tiene un pivote en cada fila entonces los vectores son LI, si no
entonces los vectores son LD.

α1
 
 . 
3. Si los vectores son LD, entonces el sistema Ax = 0 o equivalentemente A′ x = 0 tiene solución. Si x =  .. 
 
αk
es una solución a este sistema, las constantes α1 , . . . , αk satisfacen

α1 v 1 + · · · + αk v k = 0
la cual nos da una dependencia lineal entre los vectores.
Ejemplo 2.6. Determine si el conjunto de vectores es LI, si no lo es, encontrar una dependencia lineal entre
ellos.

 
 
 
 



0 
−1
2
1


 
 
 

 
 
 
 
 
1. v1 = 1 , v2 =  1  , v3 =  1  , v4 = 1

 
 
 
 





1 
2
−1
0

 
 
 



1 
0
1


 
 

 
 
 
 
2. v1 = 1 , v2 = 1 , v3 = 0

 
 
 





1 
1
0
60
Solución. 1. Necesitamos
aplicar

1
2 −1
h
i 

v 1 v 2 v 3 v 4 = 1
1
1

0 −1
2
reducción
Gauss-Jordan a la matriz

0


1, cuya forma escalonada reducida está dada por

1


1 0
3
2




A′ = 0 1 −2 −1 .


0 0 0
0
Como rango(A) = 2 < # de columnas de A entonces los vectores son LD. Para encontrar una dependencia
lineal entre estos vectores resolvemos el sistema A′ x = 0, el cual nos da las ecuaciones x1 + 3x3 + 2x4 = 0 y
x2 − 2x3 − x4 = 0 o equivalentemente
x1 = −3x3 − 2x4
x2 = 2x3 + x4 ,
con x3 y x4 son variables libres, entonces si hacemos x3 = x4 = 1 obtenemos la solución particular x1 = −5,
x2 = 3 y x3 = x4 = 1, por tanto una dependencia lineal entre los vectores está dada por
−5v1 + 3v2 + v3 + v4 = 0.

1

h
i

2. En este caso necesitamos escalonar la matriz v1 v2 v3 = 1

0
es A′ = I y por tanto rango(A) = # de columnas de A y los vectores

1


1 0, cuya forma escalonada reducida

1 1
v1 , v2 y v3 son LI.
0
Ejemplo 2.7. Determine si el conjunto de vectores dado es linealmente independiente:
(
"1#
"1#
"1#
"1# )
2 1
1
1
1
1
1
1
1
1. v1 = 1 , v2 = 1 , v3 = 1 v4 = 2 ,
2. w1 = 11 , w2 = 11 , w3 = 12 , w4 = 23 , w5 = 34
1
1
1
2
2
3
3
4
Solución.
1. Al aplicar reducción a la matriz A = [v1 v2 v3 v4 ] obtenemos la matriz A′ =
rangoA = 4 y por tanto los vectores v1 , v2 , v3 y v4 son LI.
5
4
3
2
1
"1 0 0 0#
0
0
0
0
′
1
0
0
0
2. Al aplicar reducción a la matriz A = [w1 w2 w3 w4 w5 ] obtenemos la matriz A =
0
1
0
0
0
0
1
0
, lo que implica que
1 0 0 0 1
0 1 0 0 0
0 0 1 0 0
0 0 0 1 1
, se sigue que
rangoA = 4 < # de columnas de A y por tanto los vectores w1 , w2 , w3 , w4 y w5 son LD.
Para calcular una dependencia lineal entre estos vectores debemos obtener una solución a la ecuación
Ax = 0 o equivalentemente a la ecuación A′ x = 0. Usando la matriz en forma escalonada reducida se
obtiene que una solución x = (x1 , x2 , x3 , x4 , x5 ) a la ecuación Ax = 0 satisface las ecuaciones
x1 + x5 = 0
x2 = 0
x3 = 0
y
x4 + x5 = 0
con x5 libre. Asignando el valor x5 = 1 obtenemos que x1 = −1, x2 = 0 = x3 y x4 = −1, por tanto los
vectores w1 , w2 , w3 , w4 y w5 satisfacen la relación:
−w1 − w4 + w5 = 0.
61
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Terminamos la sección con un corolario que nos será útil mas adelante.
Corolario 2.6. Un conjunto de vectores linealmente independientes de Rm tiene a lo sumo m vectores.
h
i
Demostración. Sean v1 , . . . , vk ∈ Rm vectores linealmente independientes y sea A = v1 · · · vk , dado que
las columnas de A son vectores en Rm , tenemos que la matriz tiene tamaño m × k y es obvio que rango(A) ≤
mı́n{m, k} y por el Teorema 2.5 tenemos que rango(A) = k = # de columnas, por tanto se tiene que
k = rango(A) ≤ mı́n{m, k} ≤ m.
Problemas
2.3.1. Determine cuales de los siguientes conjuntos son LI, si no lo son, encuentre una dependencia lineal entre
los vectores:
    



1 
1


    
   
a. 2 , 1

   





1 
3
      



1 
1
1


      
     
b. 2 , 1 , −1

     





−3 
1
3
     



1 
1
1


     
     
c. 2 , 1 ,  1 

     




 3
−3 
1
2.3.2. Encuentre el valor de a para los que los vectores son LI
      



1 
1
2


      
     
2 , 2 , −1 .

     





a 
3
2
      




1 1  1 




    


2 1  1 






d.   ,   ,  


3 1 −3




     




 4
1 
1
2.3.3. Determine la relación entre α y β para que los vecores v1 = (1, 0, 0), v2 = (0, 1, 0) y v3 = (α, β, α + β)
sean LD y exhiba una dependencia lineal entre los vectores.
2.3.4. Encuentre vectores v1 , v2 y v3 de tal forma que v1 , v2 sean LI y v2 , v3 sean también LI pero que v1 , v2 , v3
sean LD.
2.3.5. Sea V un espacio vectorial y sean v, w ∈ V , demuestre que {v, w} es LD si y sólo si w = cv con c ∈ R,
es decir, si w es un múltiplo de v.
2.3.6. Sean v, w ∈ R3 con v 6= 0, demuestre que
1. si v, w son LD entonces {v, w} es una lı́nea que pasa por el origen,
2. si v, w son LI entonces {v, w} es un plano que pasa por el origen.
2.3.7. Sea V un espacio vectorial, sean v1 , v2 , v3 ∈ V y sean w1 = v1 − v2 , w2 = v2 − v3 y w3 = v3 . Demuestre
que {v1 , v2 , v3 } es LI si y sólo si {w1 , w2 , w3 } es LI.
62
2.3.8. Sea V un espacio vectorial, sean v1 , v2 , v3 ∈ V vectores LI, demuestre que los vectores v1 + v2 , v2 + v3 y
v3 + v1 son LI y los vectores v1 − v2 , v2 − v3 y v3 − v1 son LD.
2.3.9. Demuestre que si el conjunto {v1 , . . . , vn } es LI y k < n entonces el conjunto {v1 , . . . , vk } también es LI.
2.3.10. Demuestre que si el conjunto {v1 , . . . , vn } es LD y vn+1 es otro vector entonces el conjunto {v1 , . . . , vn , vn+1 }
también es LD.
2.3.11. Sean v, w ∈ R3 vectores LI, demuestre que gen{v} + gen{w} es el plano que contiene a los vectores v
y w.
2.3.12. Sean v, w ∈ R3 vectores LD, demuestre que gen{v} + gen{w} es la lı́nea que contiene al vector v.
2.3.13. Demuestre que los polinomios 1, t, t2 , . . . , tn son LI.
 
 
 

0
0 0
0 1
1 0
y
, 
, 
2.3.14. Demuestre que las matrices 
0
1 0
0 0
0 0

0
 son LI.
1
2.3.15. Demuestre que el conjunto {sen(x), sen(2x), cos(x), cos(2x)} es LI.
2.3.16. Muestre que el conjunto los subconjuntos de M2 (R) son LI.
1. {E11 , E22 , E12 + E21 }.
2. {E12 , E21 , E11 − E22 }.
En general denotamos por Eij a la matriz cuya ij-ésima entrada es 1 y ceros en las demás posiciones.
2.4.
Conjuntos generadores
El concepto más importante en álgebra lineal es el concepto de base para un espacio vectorial, el cual se define
a partir de la independencia lineal y de conjunto generador. El Corolario 2.6 mostró que un conjunto linealmente
independiente en Rm tiene a lo sumo m vectores y en esta sección veremos como un conjunto generador en Rm
tiene al menos m vectores, mostrando como los dos conceptos se balancean.
Definición 2.5. Sea V un espacio vectorial, decimos que los vectores v1 , v2 , . . . , vk generan a V , si para todo
v ∈ V existen escalares α1 , α2 , . . . , αk tal que
v = α1 v 1 + · · · + αk v k .
También diremos que V es generado por el conjunto de vectores {v1 , . . . , vk }, lo cual denotaremos por V =
gen{v1 , . . . , vk }. Al conjunto {v1 , . . . , vk } se le llama conjunto generador de V .
La definición misma nos permite dar una interpretación geométrica, para dimensiones 1, 2 y 3, de conjuntos
generadores. Veremos que en general el conjunto generado por unos vectores depende de si éstos son LI o LD
63
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Conjunto generado por un vector {v}: de la definición, el conjunto generado por un vector, es el conjunto
{αv | α ∈ R}, es decir, el conjunto de múltiplos escalares de v. Sabemos de las propiedades de producto de un
escalar por un vector, que este es el conjunto de múltiplos de v y por tanto si v 6= 0 éste coincide con la lı́nea
que contiene a v. Si v = 0 entonces gen{v} = {0} el subespacio trivial. De esto se sigue que un vector no nulo
en R genera a R, pero un vector no nulo en Rm , con m ≥ 2, no es suficiente para generar este espacio.
v
Lı́nea generada por v
Conjunto generado por dos vectores v1 y v2 no nulos. Distinguimos dos casos
Caso 1: los vectores v1 y v2 son LD, o equivalentemente, uno de los vectores es un múltiplo del otro, digamos
v2 = αv1 . En este caso el conjunto generado por estos vectores, que por definición es el conjunto {βv1 + λv2 |
β, λ ∈ R}, es en realidad una combinación lineal de v1 ya que dadas la relación entre v1 y v2 obtenemos que
una combinación lineal de estos es de la forma
βv1 + λ v2 = βv1 + λαv1 = (β + λα) v1
|{z}
αv1
y obtenemos que gen{v1 , v2 } = gen{v1 } es la lı́nea que contiene a v1 .
Caso 2: los vecores son LI, o equivalentemente, ningún vector es múltiplo del otro. En este caso tenemos que
el conjunto generado por los vectores v1 , v2 , el cual por definición es el conjunto {βv1 + λv2 | β, λ ∈ R} es, por
la ley del paralelogramo, el plano que contiene a los dos vectores. Se sigue de esto que R2 es generado por dos
vectores no colineales pero dos vectores no pueden generar Rm con m ≥ 3.
v1
v2
v1
b
b
v2
Dos vectores LD generan una lı́nea
Dos vectores LI generan un plano
Conjunto generado por tres vectores {v1 , v2 , v3 }. Distinguimos dos casos
Caso 1: los vectores son LD, es decir, un vector es combibación lineal de los demás, digamos v3 = α1 v1 +α2 v2 ,
en este caso el conjunto generado por los vectores v1 , v2 , v3 que consta de los vectores de la forma β1 v1 + β2 v2 +
β3 v3 es en realidad generado por los vectores v1 y v2 ya que
β1 v 1 + β2 v 2 + β3
v3
|{z}
α1 v1 +α2 v2
= β1 v1 + β2 v2 + β3 (α1 v1 + α2 v2 ) = (β1 + β3 α1 )v1 + (β2 + β3 α2 )v2 ∈ gen{v1 , v2 }
64
y por el caso anterior, sabemos que el generado por dos vectores es una lı́nea o un plano.
Caso 2: los vectores v1 , v2 , v3 son LI. En este caso los vectores generan un espacio 3-dimensional. De esto
se sigue que tres vectores LI en R3 generan el espacio 3-dimensional, pero tres vectores no son suficientes para
generar Rm con m ≥ 4.
v3
v1
v2
v3
v1
b
v3
v1
b
b
v2
Tres vectores LD generan
una lı́nea o un plano
v2
Tres vectores LI generan
un espacio 3-dimensional
La siguiente es una caracterización que sirve para determinar cuando un conjunto de vectores es un conjunto
generador de Rm .
h
Teorema 2.7. Sean v1 , v2 , . . . , vk vectores en Rm y sea A = v1
···
i
vk la matriz cuyas columnas son los
vectores v1 , v2 , . . . , vk . Entonces el conjunto {v1 , v2 , . . . , vk } es un conjunto generador si y sólo si rango(A) =
m = # de filas de A.
Demostración. Por definición el conjunto {v1 , v2 , . . . , vk } es un conjunto generador si y sólo si para todo
 
α1
h
i 
 .. 
m
b ∈ R , existen escalares α1 , . . . , αk tal que b = α1 v1 + · · · + αk vk = v1 · · · vk  .  = Ax donde
|
{z
} 
A
αk
 
α1
 
 .. 
x =  .  , si y sólo si la ecuación Ax = b tiene solución para todo b ∈ Rm y esto, por el Teorema 1.20, es
 
αk
equivalente a que rango(A) = m = # de filas de A.
De este teorema se desprende un procedimiento para determinar si un conjunto de vectores es un conjunto
generador de Rm , el cual describimos a continuación.
Procedimiento 2.2. (Procedimiento para determinar si un conjunto de vectores de Rm es un
conjunto generador) Sean v1 , v2 , . . . , vk vectores en Rm , entonces
h
1. Forme la matriz A = v1
···
i
vk .
2. Aplique reducción Gauss-Jordan a A para calcular la forma escalonada reducida A′ de A.
3. Si A′ tiene un pivote en cada fila, entonces los vectores v1 , v2 , . . . , vk generan a Rm , de otra forma no
generan.
65
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Ejemplo 2.8. Determine si el conjunto de vectores genera a R3 ,

 
 


 



−1 
0
−2
1



 
 


 
 
 


 
1. v1 = 2 , v2 =  −4  , v3 = 1 , v4 =  0 

 
 


 





−3 
1
−10
5

 
 
 



0 
−2
1


 
 
 

 
 
 
2. v1 = 2 , v2 = −4 , v3 = 1

 
 
 





1 
−9
5
Solución.
h
i
1. Siguiendo los pasos indicados en el procedimiento, primero formamos la matriz A = v1 v2 v3 v4 =


1 −2 0 −1




2 −4 1
0  . Ahora calculamos la matriz escalonada reducida de A, usando MatLab obtenemos


5 −10 1 −3
>> A = [1 − 2 0 − 1; 2 − 4 1 0; 5 − 10 1 − 3]; rref (A)
ans =


1 −2 0 −1




0
0 1
2


0
0 0
0
Como rango(A) = 2 < 3 = # de filas, entonces los vectores no

1 −2
h
i 

2. En este caso formamos la matriz A = v1 v2 v3 = 2 −4

5 −9
reducida de A, usando MatLab obtenemos
generan a R3 .

0


1 . Ahora calculamos la matriz escalonada

1
>> A = [1 − 2 0; 2 − 4 1; 5 − 10 1]; rref (A)
ans =


1 0 0




0 1 0


0 0 1
Como rango(A) = 3 = # de filas, entonces estos vectores generan a R3 , es decir, gen{v1 , v2 , v3 } = R3 .
Corolario 2.8. Sean v1 , v2 , . . . , vk vectores en Rm , si k < n entonces los vectores v1 , v2 , . . . , vk no generan a
Rm .
h
Demostración. Sea A = v1
···
i
vk , entonces rango(A) ≤ k < m = # de filas de A, entonces por el
Teorema 2.7, el conjunto no genera a Rm .
El siguiente corolario es la versión del Corolario 2.6 para conjuntos generadores.
Corolario 2.9. Un conjunto generador de Rm tiene al menos m vectores.
66
Teorema 2.10. Si los vectores v1 , . . . , vm ∈ Rm son linealmente independientes, entonces generan a Rm , es
decir, gen{v1 , . . . , vm } = Rm .
h
Demostración. Sea A = v1
···
i
vm , como los vectores v1 , . . . , vm son linealmente independientes entonces,
por el Teorema 2.5, se tiene que rango(A) = m = # de columnas, pero la matriz A es de tamaño m × m, por
tanto # de filas=# de columnas. Luego rango(A) = m = # de filas de A. Por tanto por el Teorema 2.7 los
vectores v1 , . . . , vm generan a Rm .
 
 
 
1
0
1
 
 
 
 
 
 
Ejemplo 2.9. En el Ejemplo 2.6 se encontró que los vectores v1 = 1 , v2 = 1 y v3 = 0 son linealmente
 
 
 
1
1
0
3
independientes, entonces por el teorema anterior se tiene que estos vectores generan R .
Problemas
2.4.1. Determine si el conjunto de vectores genera a R3 .
        
     







1 
3
−1
1
3
−1
1




        
     
       
     
b. 1 ,  1  , 1 , 2
a. 1 ,  1  , 1


       
     








 2

2 
2
2
2 
2
2
2.4.2. Determine si el conjunto de vectores genera a R4
        



 1  1 2 1





      


−1 1 2 0








a.   ,   ,   ,  
b.



3  1 2 1




       



 1
2
2
0 
       



 1  1 2  1 





      


−1 1 2  7 
 , , , 
       


 3  1 2 −5



       




 1
2
2
3 
2.4.3. Sea V un espacio vectorial, sean v1 , v2 , v3 ∈ V y sean w1 = v1 − v2 , w2 = v2 − v3 y w3 = v3 . Demuestre
que el conjunto {v1 , v2 , v3 } genera a V si y sólo si el conjunto {w1 , w2 , w3 } genera a V .
2.4.4. Sea V un espacio vectorial y sean v1 , . . . , vk ∈ V , el conjunto generado por los vectores v1 , . . . , vk se
define como
gen{v1 , . . . , vk } = {α1 v1 + · · · + αk vk | α1 , . . . , αk ∈ R }.
Demuestre que gen{v1 , . . . , vk } es un subespacio de V .
2.4.5. Sea V un espacio vectorial y sean v1 , . . . , vk , w1 , . . . , wl ∈ V , demuestre que
gen{v1 , . . . , vk } + gen{w1 , . . . , wl } = gen{v1 , . . . , vk , w1 , . . . , wl }.
2.4.6. Demuestre que los polinomios 1, t, t2 , . . . , tn generan a Pn .
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

2.4.7. Demuestre que las matrices 
1
0
 
 
0
0 1
0
, 
, 
1
0 0
0
67

 
0 0
0
 generan a M2 (R).
y
0 1
0
2.4.8. Demuestre que S2 (R) = gen{E11 , E22 , E12 + E21 } y A2 (R) = gen{E12 − E21 }.
2.4.9. sl2 (R) = gen{E12 , E21 , E11 − E22 }.
2.5.
Bases
Al unir los conceptos de independencia lineal y conjunto generador se consigue uno de los conceptos más
importantes del álgebra lineal: el concepto de base de un espacio vectorial el cual definimos a continuación.
Definición 2.6. Sea V un espacio vectorial y sean v1 , . . . , vn ∈ V , decimos que el conjunto {v1 , . . . , vn } es una
base para V si
1. los vectores v1 , . . . , vn son linealmente independientes,
2. los vectores {v1 , . . . , vn } generan a V .
De los Corolarios 2.6 y 2.9 de las secciones anteriores tenemos lo siguiente.
Teorema 2.11.
1. Toda base de Rm tiene exactamente m vectores.
2. Un conjunto de m vectores linealmente independientes de Rm es una base.
Demostración.
1. Se sigue de los corolarios 2.6 y 2.9.
2. Se sigue de el Teorema 2.10.
 
 
 
0
−2
1
 
 
 
 
 
 
Ejemplo 2.10. En el ejemplo anterior se comprobó que los vectores v1 = 2 , v2 = −4 y v3 = 1 son
 
 
 
1
−9
5
linealmente independientes, por tanto generan y forman una base para R3 .
El último teorema garantiza que todas las bases de Rm tienen m vectores, en general para todos los espacios
vectoriales con un número finito de generadores (también llamados finito dimensionales) se cumple que todas las
bases tienen exactamente el mismo número de elementos. Abajo en el Teorema 2.15 se demostrará este hecho
para subespacios de Rm , el caso general se demostrará en la Sección 3.4. Por ahora daremos un argumento
computacional que nos permitirá determinar si un conjunto de vectores es una base para Rm .
h
i
Teorema 2.12. Sean v1 , . . . , vm ∈ Rm y A = v1 · · · vm entonces el conjunto {v1 , . . . , vm } es una base
para Rm si y sólo si rango(A) = m.
La demostración de este teorema es una aplicación inmediata de los Teoremas ?? Tenemos además el siguiente corolario.
68
h
Corolario 2.13. an v1 , . . . , vm ∈ Rm y A = v1
Rm si y sólo si A es invertible.
···
i
vm entonces el conjunto {v1 , . . . , vm } es una base para
Demostración. La demostración se sigue del teorema anterior y el Corolario 1.22.
Nuevamente este teorema da un procedimiento para determinar si un conjunto de vectores es una base, el cual
consiste en formar una matriz con los vectores dados y determinar si el rango de esta matriz es el # de filas e
igual al # de columnas. Como lo mostramos en el siguiente ejemplo.
Ejemplo 2.11. Determine en cada caso si el conjunto de vectores dados forma una base para R3 .


 
 
 
 
 
 







1
−2
1
1
1
1 



 
 
 


 
 
 

 
 
 
 
 
 
1. v1 = −1 , v2 =  2  , v3 = 1
2. v1 = −1 , v2 = 2 , v3 = 1


 
 
 
 
 
 










3
−6
4 
3
3
4 
Solución.

1
−2
1





1. Al aplicar reducción Gauss-Jordan a la matriz A = −1
2 −1 formada por los vectores v1 , v2 y v3 ,


3 −6
3


1 −2 0




obtenemos la matriz 0
0 1. Esta matriz tiene rango 2 y por tanto los vectores v1 , v2 y v3 no forman


0
0 0
una base para R3 , ya que no son LI.


1 1 1




2. El aplicar reducción Gauss-Jordan a la matriz A = −1 2 1, formada por los vectores v1 , v2 y v3 ,


3 3 4


1 0 0




obtenemos la matriz 0 1 0 . Como esta matriz tiene rango 3, entonces los vectores v1 , v2 y v3 forman


0 0 1
una base para R3 , ya que son LI y tres vectores LI generan a R3 .
Problemas
2.5.1. Encuentre una base de R4 que contenga los vectores (1, 2, −2, 1) y (1, 0, −2, 2).
2.5.2. Calcule una base del subespacio {p ∈ R4 [t] |
R1
0
p(x)dx = 0} de R4 [t].
2.5.3. Muestre que el conjunto {E12 , E21 , E11 + E22 } es una base de S2 (R).
2.5.4. Muestre que el conjunto {E12 , E21 , E11 − E22 } es una base de sl2 (R).
69
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
2.5.5. Demuestre que {Eij + Eji | 1 ≤ i < j ≤ n} ∪ {Eii | 1 ≤ i ≤ n} es una base de Sn (R).
2.5.6. Demuestre que {Eij − Eji | 1 ≤ i < j ≤ n} es una base de An (R).
2.5.7. Demuestre que {Eij | 1 ≤ i ≤ n} ∪ {Ejj − Ej+1,j+1 | 1 ≤ j < n} es una base para sln (R).
2.5.8. Sea V un espacio vectorial y X ⊆ Y ⊆ V tal que X es LI y V = genY entonces existe una base Z tal
que X ⊆ Z ⊆ Y . En particular si Y es una base muestre que existe S ⊆ Y tal que XU S es una base de V .
2.6.
Subespacio generado por un conjunto de vectores
Cuando se tiene un conjunto de vectores en Rm , el conjunto de combinaciones lineales de estos es un
subespacio, el cual podrı́a ser todo Rm en el caso de que estos generen o un subespacio propio, si estos no generan
a Rm . Al conjunto de combinaciones lineales de un conjunto de vectores se le llama el conjunto generado por
los vectores y lo definimos a continuación.
Definición 2.7. Sea V un espacio vectorial y sean v1 , . . . , vk ∈ V , definimos el conjunto generado por estos
vectores, denotado por gen{v1 . . . , vk }, como el conjunto de combinaciones lineales de los vectores v1 , . . . , vk .
Esto es,
gen{v1 . . . , vk } = {α1 v1 + · · · + αk vk | α1 , . . . , αk ∈ R } .
Es fácil mostrar que el conjunto generado por los vectores v1 , . . . , vk ∈ V es un subespacio de V , ver Problema
2.4.4, por esta razón al conjunto gen{v1 . . . , vk } lo llamaremos el subespacio generado por los vectores v1 , . . . , vk .
A continuación demostramos que todo subespacio de Rm tiene una base finita y en consecuencia todo subes-
pacio H de Rm es el subespacio generado por un conjunto finito de vectores, es decir, existen vectores v1 ,
. . . , vk ∈ Rm tal que H = gen{v1 , . . . , vk }.
Teorema 2.14. Sea H 6= {0} un subespacio de Rm , entonces existen vectores v1 , . . . , vk ∈ Rm tal que
{v1 , . . . , vk } es una base de H.
Demostración. Sea 0 6= v ∈ H, si H = gen{v} terminamos, si no, existe v2 ∈ H \ gen{v}.
Si H = {v, v2 } terminamos la demostración, si no, tomamos v3 ∈ H \ gen{v, v2 }. Continuando de manera
inductiva obtenemos vectores v1 , . . . , vk tal que H = gen{v, v2 , . . . , vk }
Debemos demostrar que los vectores son linealmente independientes. Por inducción nótese que {v} es LI, ya
que si αv = 0, como v 6= 0 entonces tenemos que α = 0.
Ahora, supongamos que el conjunto {v, v2 , . . . , vk−1 } es LI y veamos que {v, v2 , . . . , vk−1 , vk } es LI. Para
esto supongamos que
αv + α2 v2 + · · · + αk vk = 0.
(2.3)
Veamos por el absurdo que αk = 0 ya que si αk 6= 0 tenemos que αk vk = −α1 v1 − · · · − αk−1 vk−1 y por
tanto
vk = −
α1
αk−1
v1 − · · · −
vk−1 ∈ gen{v1 , . . . , vk−1 }
α
α
70
lo que contradice la escogencia del vector vk .
Se sigue que αk = 0 y la Ecuación 2.3 se reduce a αv + α2 v2 + · · · + αk−1 vk−1 = 0 y como {v, v2 , . . . , vk−1 }
es LI tenemos que α2 = · · · = αk−1 = 0 y por tanto {v, v2 , . . . , vk−1 , vk } es LI.
El hecho de que los vectores v1 , . . . , vk son LI para todo k garantiza que el proceso termina en un número
finito de pasos, de hecho se pueden tomar a lo sumo m vectores de esta forma, esto es debido a que los vectores
v1 , . . . , vk ∈ Rm entonces el Corolario 2.6 garantiza que k ≤ m.
Concluimos que el conjunto {v, v2 , . . . , vk } es una base de H y k ≤ m.
La demostración de este teorema se puede adaptar para demostrar que todo subespacio de un espacio vectorial
con una base finita tiene una base finita. Existe también una demostración de que todo espacio vectorial tiene
una base usando el Axioma de elección.
De este teorema deducimos además que todo subespacio de Rm tiene una base con a lo sumo m vectores,
veamos que el número de vectores en una base es un invariante, al cual llamaremos la dimensión del subespacio.
Teorema 2.15. Sea V un subespacio de Rm y sean {v1 , . . . , vk } y {w1 , . . . , wl } bases para V , entonces k = l.
Es decir, todas las bases de V tienen exactamente el mismo número de vectores.
Demostración. Primero supongamos que l > k, como los vectores v1 , . . . , vk forman una base para V , entonces
por definición de base tenemos que V = gen{v1 , . . . , vk } y por tanto para i = 1, . . . , l existen constantes
α1i , . . . , αki tal que
h
wi = α1i v1 + · · · + αki vk = v1
Uniendo estas ecuaciones obtenemos:
h
w1
···
i h
wl = v 1
···

α11
i
 ..
vk  .

αk1
···
..
.
···
···

α1i
i 
 . 
vk  ..  .
 
αki


α1l
 h
.. 
= v1
. 

αkl
···
i
vk A,
(2.4)


α11 · · · α1l


.. 
 .
..
donde A =  ..
. Como l > k, entonces el sistema Ax = 0 tiene mas variables que ecuaciones y por
.
. 


αk1 · · · αkl
tanto este sistema tiene al menos una solución no trivial, es decir, exiten constantes no todas nulas β1 , . . . , βl
tal que

  
β1
0
   
 ..   .. 
A  .  = . .
   
βl
0
(2.5)
71
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO


β1
 
.
Luego, multiplicando la Ecuación (2.4) a la derecha por  .. , obtenemos
 
βl
h
w1

β1
i  h
.
wl  ..  = v1
 
βl

···
···
vk

β1
 
.
A  .. 
 
βl
| {z }

i
h
= v1
=0 por Ec. (2.5)
···
   
0
0
i   
 ..   .. 
vk  .  =  .  .
   
0
0
  
0
β1
h
i   
 ..   .. 
Es decir w1 · · · wl  .  =  . , este último sistema es equivalentemente, por el Lema 1.9, a la ecuación
   
0
βl
β1 w1 + · · · + βl wl = 0, y se sigue que los vectores w1 , . . . , wl son linealmente dependientes lo que contradice el

hecho de que forman una base para V , por tanto k ≤ l.
De igual forma se demuestra que l ≤ k y por tanto k = l.
Este lema motiva la siguiente definición.
Definición 2.8. Definimos la dimensión de un subespacio de H de Rm , la cual denotaremos por dim H, como
el número de elementos en una base de H.
Problemas
2.6.1. Sea V un espacio vectorial, sean v1 , v2 , v3 ∈ V y sean u1 = v1 − v2 , u2 = v2 − v3 y u3 = v3 . Demuestre
que el conjunto {v1 , v2 , v3 } genera a V si y sólo si el conjunto {u1 , u2 , u3 } genera a V .
2.6.2. Sean H y K subespacios de Rn con dim H = dim K y H ⊆ K. Demuestre que H = K.
2.6.3. Sean v1 , . . . , vk ∈ Rn y V = gen{v1 , . . . , vk } entonces dim H ≤ k.
2.7.
Subespacios fundamentales
Dada una matriz A se pueden definir cuatro subespacios determinados por esta, los cuales definimos a
continuación.
Definición 2.9. Sea A una matriz de tamaño m × n definimos los siguientes subespacios:
1. El espacion nulo de A, denotado N ul(A), se define como
N ul(A) = {x ∈ Rn | Ax = 0.}
72
2. El espacio columna, denotado Col(A), se define como
Col(A) = gen{c1 , . . . , cn },
donde c1 , . . . , cn son las columnas de A.
3. El espacio fila de A, denotado por F il(A), se define como
t
F il(A) = gen{f1t , . . . , fm
},
donde f1 , . . . , fm son las filas de A.
4. El espacio nulo a izquierda de A, denotado por N uliz(A), se define como
N uliz(A) = {x ∈ Rm | At x = 0.}
De acuerdo al Problema 2.4.4, el espacio columna, Col(A), y el espacio fila, F il(A), de una matriz A son
subespacios de Rm y Rn , respectivamente, y por el Problema 2.2.8 los conjuntos N ul(A) y N uliz(A) también
son subespacios de Rn y Rm , respectivamente.
El propósito ahora es dar un procedimiento que nos permita hallar una base para los subespacios fundamentales.
Calcular el espacio nulo de una matriz A es mas sencillo, ya que los vectores x en este espacio son solución a la
ecuación Ax = 0, o equivalentemente, la ecuación A′ x = 0 con A′ la esaclonada reducida de A. El procedimiento
para calcular una base para el espacio columna se sigue del siguiente teorema.
Teorema 2.16. Sea A una matriz de tamaño m × n y sea A′ la forma escalonada reducida de A. Entonces los
vectores para los cuales la columna de A′ tiene un pivote, forman una base para Col(A) y por tanto dim Col(A) =
rango(A). Además se tiene que dim N ul(A) = n − rango(A).
Demostración. Sea k = rango(A), sin pérdida de generalidad, supongamos que las primeras k columnas de
A′ tienen pivote, es decir
1
 ..
.
′
0
A =
0
.
..
··· 0 b1,k+1 ··· b1n
. . ..
..
..
.
··· 1 bk,k+1
··· 0
0
. . ..
..
0 ··· 0
..
.
0

.
. .. 

··· bkn 
··· 0 
. . .. 
. .
..
···
(2.6)
0
Sean c1 , . . . , cn las columnas de A, vamos a demostrar que los vectores c1 , . . . , ck forman una base para Col(A).
Primero nótese que los vectores c1 , . . . , ck son linealmente independientes ya que éstos forman las primeras
i
h
columnas de A y por tanto la forma escalonada reducida de la submatriz c1 · · · ck está dada por las
primeras k filas de A′ y de la Ecuación (2.6), se obtiene que ésta tiene un pivote en cada columna, luego por el
Teorema 2.5, los vectores c1 , . . . , ck son linealmente independientes.
Antes de demostrar que estos vectores generan el espacio columna, calculemos una base para el espacio nulo.
73
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO


x1
 
 . 
Para esto tomemos x =  .. , de la Ecuación (2.6) tenemos lo siguiente
 
xn

x1
 
 .. 
 .  ∈ N ul(A) si y sólo si Ax = 0 si y sólo si A′ x = 0 si y sólo si
 
xn

x1 +b1,k+1 xk+1 +···+b1n xn =0
..
.
xk +bk,k+1 xk+1 +···+bkn xn =0
x1 =−b1,k+1 xk+1 −···−b1n xn
..
.
xk =−bk,k+1 xk+1 −···−bkn xn
 −b

 x1   −b1,k+1 xk+1 −···−b1n xn 
 −b1n 
1,k+1
..
.
.
.

 . 
..
 .  
 .. 
. 


 xk  

−bk,k+1 xk+1 −···−bkn xn 
−bkn 
 −bk,k+1 
si y sólo si  xk+1  = 
 . (2.7)
xk+1
 = xk+1  1  + · · · + xn 
0 
 .  



 . 
.
.
..
..
..
..
si y sólo si
xn
xn
1
0
 −b
 −b


 −b1n 
 −b1n 
1,k+1
1,k+1






.
.
.
.
 . 


 .. 

 .. 

 . 
 .. 



−bkn  . Nótese además que los vectores  −bk,k+1  , . . . ,  −bkn 
−bk,k+1 
Entonces N ul(A) = gen 

 1 
 1 ,...,
0 

 0 



 . 
 . 


.
.


..
..
..
..


1
0
0
1
son claramente LI y por tanto forman una base para N ul(A). De esto se sigue que los vectores c1 , · · · , cn
satisfacen las ecuaciones

 −b
 
1,k+1
0
 ..  h
 
 . 
 .. 
−bk,k+1 
. = A 
 1  = c1
 
 . 
..
0
···
0
..
.
 
 −b1n 
0
.
 
 ..  h
 .. 
 −bkn 
 .  = A  0  = c1
 


..
0
.
1
 −b
1,k+1

. 
i
 .. 
−bk,k+1 

cn  1 
 . 
..
0
···
 −b1n 
.
i  .. 
 −bkn 
cn  0 


..
.
1
Por el Lema 1.9 tenemos que estas ecuaciones matriciales son equivalentes a las ecuaciones
−b1,k+1 c1 − · · · − bk,k+1 ck + ck+1 = 0
−b1n c1 − · · · − bkn ck + cn = 0
o equivalentemente
ck+1 = b1,k+1 c1 + · · · + bk,k+1 ck
o equivalentemente
cn = b1n c1 + · · · + bkn ck
..
.
Obtenemos que cada uno de los vectores ck+1 , . . . , cn es una combinación lineal de los vectores c1 , . . . , ck . Por
74
tanto si x ∈ Col(A), obtenemos que
x =α1 c1 + · · · + αk ck + αk+1 ck+1 + · · · + αn cn
=α1 c1 + · · · + αk ck + αk+1 (b1,k+1 c1 + · · · + bk,k+1 ck ) + · · · + αn (b1n c1 + · · · + bkn ck )
=(α1 + αk+1 b1,k+1 + · · · + αn b1n )c1 + · · · + (αk + αk+1 bk,k+1 + · · · + αn bkn )ck ∈ gen{c1 · · · , ck }
Concluimos que ColA = gen{c1 , . . . , ck }, entonces los vectores c1 , . . . , ck generan a Col(A) y como son linealmente independientes entonces forman una base para Col(A).
Finalmente, observese que dim Col(A) = k = rango(A) y por la Ecuación (2.7) tenemos que dim N ul(A) =
n − k = n − rango(A).
De este resultado se desprende el siguiente corolario el cual será clave para la demostración del Teorema
3.20, el cual es uno de los teoremas más importantes del álgebra lineal.
Corolario 2.17. Sea A una matriz de tamaño m × n, entonces
dim Col(A) + dim N ul(A) = n = # de columnas de A.

1
−1 0


Ejemplo 2.12. Calcule los cuatro subespacios fundamentales de la matriz A = 2 −2 1

3 −3 1
Calculando la forma escalonada reducida de A obtenemos






1 −1 0 1
1 −1 0 1
1 −1 0 1












0
2 −2 1 4 −2F1 +F2 →F2 0
0 1 2
0 1 2






0 0 0
3 −3 1 5 −2F1 +F3 →F3 0 0 1 2 −F2 +F3 →F3 0

1


4. Solución:

5
entonces por el teorema anterior la primera y tercera columna de A forman una base para el espacio columna
de A, es decir
    



0 
1


    
   
Col(A) = gen 2 , 1 .

   





1 
3
Ahora para el espacio nulo resolvemos el sistema Ax = 0 o equivalentemente A′ x = 0 y obtenemos lo siguiente
 
 
x
 1
   0
x   
x1 = x2 − x4
x1 − x2 + x4 = 0
′  2
A   =  0 ⇔
⇔
x3   
x3 + 2x4 = 0
x3 = −2x4
 
0
x4
 
 

  
−1
1
x2 − x4
x1
 
 

  
 
 

  
 1
1

x2   x2
 = x2   + x4   .
 
⇔
 
 

 =
−2
0
x3   −2x4 
 
 

  
1
0
x4
x4
75
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
    



−1 
1



   








1  1 




Por tanto N ul(A) = gen   ,   .



0 −2



   




 0
1 
Para calcular el espacio fila y el nulo


1
2
3




−1 −2 −3 F1 +F2 →F2




 0
1
1


1
4
5 −F1 +F4 →F4
a izquierda, calculamos la escalonada reducida de At





1 2 3 −2F2 +F1 →F1 1 0
1 2 3










0 1
 0 1 1
 0 0 0







 F2 ↔F3 

0 0
 0 0 0
 0 1 1





0 2 2 −2F2 +F4 →F4 0 0
0 2 2
1



1


0

0
    


 


  1   2 




x

  

 1
−1 −2


  
Se sigue que F il(A) = gen 
x2  satisface la ecuación At x = 0 si y
  ,   , además un vector x = 




 0   1 



   


x
3


 1
4 
solo si
 
  
  
0
 
x
−x
x1
−1

 1  3  
  


x
+
x
=
0
x
=
−x
0
1
3
1
3








⇔
⇔ x2  = −x3  = −1 .
⇔
At x2  = 




  



 0
x2 + x3 = 0
x2 = −x3
 
x3
x3
x3
1
0
  



−1 

  

 
Por tanto N uliz(A) = gen −1 .

 



 1 



El siguiente teorema nos permite calcular bases alternativas para el espacio columna y el espacio fila de una
matriz.
Teorema 2.18. Sea A una matriz, entonces tenemos que F ilA = F ilA′ donde A′ es la forma escalonada
reducida de A, además se tiene que dim F ilA = rango(A). Es decir, el espacio fila de una matriz coincide con
el espacio de su forma escalonada reducida.
Demostración. Sean f1 , . . . , fm las filas de A y sean f1′ , . . . , fk′ las filas no nulas de A′ , entonces k = rango(A).
Como A′ se obtiene de A aplicando operaciones elementales de fila, las cuales envuelven combinaciones lineales
de filas de A, entonces tenemos que fi′ ∈ gen{f1 , . . . , fm }, para i = 1, . . . , k. De esto se deduce que F ilA′ ⊆ F ilA.
Ahora, como las operaciones elementales son reversibles y podemos recuperar la matriz A de A′ por medio
de operaciones elementales, entonces tenemos que fi ∈ gen{f1′ , . . . , fk′ }, para i = 1, . . . , m. Deducimos que
F ilA ⊆ F ilA′ y por tanto F ilA′ = F ilA.
Es fácil ver que los vectores f1′ t , . . . , fk′ t son LI ya que la matriz A′ está en forma escalonada reducida y los
pivotes están en diferentes columnas, por tanto estos forman una base de A, concluimos que dim F ilA = k =
rango(A).
76
Corolario 2.19. Sea A una matriz de tamaño m × n, entonces rango(A) = rango(At ).
Demostración. De la definición de espacio fila y espacio columna tenemos que F il(A) = Col(At ) y por el
teorema anterior dim F il(A) = rango(A) y por el Teorema 2.16 tenemos que dim Col(At ) = rango(At ), por
tanto
rango(A) = dim F il(A) = dim Col(At ) = rango(At ).

1 −1
0 1



1 4 la matriz del Ejemplo 2.12. En ese ejemplo se calculó que las matrices

1 5




1 0 1


1 −1 0 1





0 1 1


t ′
t
′

 y como
escalonadas reducidas de A y A respectivamente son A = 0
0 1 2 y (A ) = 



 0 0 0


0
0 0 0
0 0 0

 
 



0 
1


 

 




Col(A) = F il(At ) = F il(At )′ se tiene que Col(A) = gen v1 = 0 , v2 = 1 . Se deja como ejercicio al

 
 





1 
1
lector verificar que v1 = c1 − 2c3 y v2 = c3 , donde c1 y c3 son la primera y tercera columna de la matriz A, lo


Ejemplo 2.13. Sea A = 2 −2

3 −3
que verifica que en realidad el espacio generado por v1 y 
v2 es igual
de A.

 espacio columna
 al



0 
1


 
 














0
−1
 , w2 =   . Se deja como ejercicio al
Además F il(A) = F il(A′ ), entonces F il(A) = gen w1 = 






1
 0




 
 





2 
1
lector verificar que w1 = f1 y w2 = −2f1 + f2 donde f1 y f2 son la primera y segunda fila de A. Lo que verifica
que el espacio generado por w1 y w2 es igual al espacio fila de A.
AGREGAR EJEMPLO MATLAB
Problemas
2.7.1. Encuentre los cuatro subespacios fundamentales de la matriz





1 2
1
1 −2
1 −2










a. A = −2
4  c. C = 5 6
4  b. B = −2 −2





9 10
1
9
2
1
2
3
7
11
Encuentre una base para el subespacio solución del sistema lineal
a.
2x1 − x2 + 3x3
=0
−4x1 + 2x2 − 6x3
=0
b.
2x1 − x2 + 3x3
=0
x1 + x2 − x3
=0
4



8

12
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
77
Ayuda: Escriba el sistema en la forma Ax = 0, por el Ejercicio 2.2.4 tenemos que x es solución al sistema si y
sólo si x ∈ N ul(A).
2.7.2. Sean A y B matrices tal que AB = 0, demuestre que Col(B) ⊆ N ul(A) y F il(B) ⊆ N uliz(A).
2.7.3. Determine las dimensiones de los cuatro subespacios fundamentales de una matriz que satisface:
a. A es 8 × 7 con rango 5.
b. A es 7 × 5 con rango 5.
2.7.4. Determine el tamaño de A para que dim N ulA = dim N ulizA + 1.
2.7.5. muestre que b ∈ ColA si y sólo si Ax = b tiene solución. (El espacio columna es el espacio solución a la
ecuación Ax = b).
2.7.6. Demuestre o de un contraejemplo de las siguientes afirmaciones
1. Si las columnas de A son LD también lo son las filas de A.
2. Si las columnas de A son LI también lo son las filas de A.
3. Si X es una base de Rn y W ⊆ Rn es un subespacio entonces un subconjunto de X es una base de W .
2.7.7. Si A = [I2 I2 ] determine ColA y N ulA.
2.7.8. Si A es 3×4 con N ulA = gen{(1, 1, −1, 0)} determine lo siguiente
1. rangoA,
2. la forma escalonada A′ de A,
3. F ilA

1 1
1 0





2.7.9. Si A′ = 0 0 0 1, cuales de los subespacios N ulA, N ulizA, ColA y F ilA se pueden determinar y


0 0 0 0
que se puede decir de los demas.
2.7.10. Determine el espacio columna en los siguientes casos
1. si A es 3 × 6 y Ax = b tiene solución para todo b,
2. si A es 4×4 y Ax = 0 tiene solución única,
3. A es 2 × 3 y A tiene una inversa a derecha.
2.7.11. Sea A una matriz 4 × 3, si N ulA = gen{(1, 1, −1), (1, 0, 0)} determine la forma escalonada reducida A′
de A y una base para F ilA.
2.7.12. Sea A ∈ Mn (R), Nk = N ul(Ak ) y Ck = Col(Ak ), demuestre que para todo k ≥ 1 se tiene que
78
1. Nk ⊆ Nk+1
2. Ck+1 ⊆ Ck
2.7.13. Si A ∈ Mmn (R) es una matriz, muestre que
Col(A) = {Ax | x ∈ Rn } = ({b | existe x tal que b = Ax})
Este ejercicio muestra que el espacio columna es el conjunto solución de la ecuación Ax = b.
2.7.14. Sea A ∈ Mmn (R) y B ∈ Mnq (R), muestre que lo siguiente
1. Col(AB) ⊆ Col(A) y deduzca que rango(AB) ≤ rango(A)
2. Si B tiene inversa a la derecha, en particular si B es invertible, entonces Col(AB) = Col(A). Concluya
que en este caso se tiene que rango(AB) = rango(B).
2.7.15. Sea A ∈ Mmn (R) y B ∈ Mnq (R), muestre que lo siguiente
1. rango(AB) ≤ rango(B). (Ayuda: Use el hecho que rango(At ) = rango(B t ).)
2. rango(AB) ≤ mı́n{rango(A), rango(B)}
3. Si B es invertible entonces rango(BA) = rango(A).
2.7.16. Sean A, B ∈ Mn (R) con B invertible, demuestre que rango(A) = rango(B −1 AB).
2.7.17. Si A es m × p y B es p × q con m < p < q y AB = 0, muestre que rangoA + rangoB ≤ m.
2.7.18. De un ejemplo de dos matrices A y B tal que Col(AB) 6= Col(A).
2.7.19. Si A es 8 × 10 con rango 6 determine las dimensiones de N ulA y N ulizA. Repetir si A es (m + 1) × m
con rango m − 1.
2.8.
Subespacio generado
En esta sección abordaremos dos preguntas acerca de un subespacio H generado por vectores v1 . . . , vn en
m
R , las primera de las cuales es:
1. Si los vectores v1 , . . . , vn no son linealmente independientes, como encontrar una base para H.
h
i
Si hacemos A = v1 · · · vn entonces Col(A) = gen{v1 , . . . , vn } = H y aplicando el Teorema 2.16 obtenemos
una base para Col(A) = H.
 


 
0
−2
1
 


 
 


 
Ejemplo 2.14. Calcular una base para H = gen{v1 , v2 , v3 } donde v1 = 2 , v2 =  −4  y v3 = 1 .
 


 
1
−10
5
79
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

1
−2 0


1




−5 1 obtenemos A′ = 0


0
−5 1


Solución. Aplicando reducción Gauss-Jordan a la matriz A = 2

5
Entonces los vectores v1 y v3 forman una base para H.
−2 0
0
0



1 .

0
La segunda pregunta es conocida como el Test de membresı́a y dice lo siguiente.
2. Si H es un subespacio de Rm con base {v1 , . . . , vk } y b es un vector en Rm , como determinar si b ∈ H.
h
Haciendo A = v1
i
tenemos que b ∈ H si y sólo si existen constantes α1 , . . . , αk tal que b =
 
 
α1
α1
 
h
i 
 .. 
 .. 
α1 v1 + · · · + αk vk = v1 · · · vk  .  = Ax con x =  . . En otras palabras, b ∈ H si y sólo si la ecuación
 
 
αk
αk
 
α1
 
 .. 
Ax = b tiene solución y si x =  .  es una solución a esta ecuación, entonces b = α1 v1 + · · · + αk vk .
 
αk

 
 
 




1
0
1


 
 

 
 
 
 
Ejemplo 2.15. Sea H = gen v1 = 2 , v2 = 1 y sea b = −2, determinar si b ∈ H, en caso afirmativo

 
 
 





1
1 
5
expresar a b como combinación lineal de v1 y v2 .


···
vk
1


Solución. Aplicando reducción Gauss-Jordan a la matriz 2

5

1 0


2 1

5 1
1



−2

1
−2F1 +F2 →F2
−5F1 +F3 →F3

1 0


0 1

0 1
1



−4

−4
0
1


1 −2 obtenemos

1
1

−F2 +F3 →F3
1 0


0 1

0 0
1



−4

0
se sigue que la ecuación Ax = b tiene solución α1 = 1 y α2 = −4, por tanto b = v1 − 4v2 .
En el siguiente ejemplo se muestra que algunas veces los subespacios de Rn aparecen como el espacio nulo de
una matriz.
Ejemplo 2.16. Calcular una base para cada uno de los siguientes subespacios.
 

 x 
1. H =   y = mx, m ∈ R
 y


 




x



   
2. H = y  x = at, y = bt y z = ct, a, b, c ∈ R .


 





 z
80

 




x



   
3. H = y  ax + by + cz = 0, a, b, c ∈ R, c 6= 0


 





 z
 





x


  
 
4. H = y  x + y + z = 0, 2x − y − z = 0 .


 




 z

 
 
 
   
 
1
x
1
x
x
x
1.   ∈ H si y sólo si y = mx si y sólo si   =   = x   si y sólo si   es un múltiplo de  .
1
y
m
mx
y
y
  
 1 
Por tanto H = gen   .
 1 
 
 
   
 
x
a
at
x
x
 
 
   
 
 
 
   
 
2. y  ∈ H si y sólo si x = at, y = bt y z = bt si y solo si y  =  bt  = t  b  si y sólo si y  es un múltiplo
 
 
   
 
z
c
ct
z
z
  
 



a

  a 


 
 
 
de  b . Por tanto H = gen  b  .

 
 




 c 
c
 
  
 

x
x
x
1
 
  
 

 
  
 

a
b
3. y  ∈ H si y sólo si ax + by + cz = 0 si y sólo si z = − c x − c y si y sólo si y  = 
 = x 0 +
y
 
  
 

z
− ac x − cb y
z
− ac
   

   
 
 



1
1
x
0
0 
0

   
    

 
 
   
   
 
 
y  1  si y sólo si y  es una combinación lineal de  0  y  1 . Por tanto H = gen  0  ,  1  .

   
   
 
 



b 
 −a

− ac
z
− cb
−
− cb
c
c
 
 
 
 x

x
 
 
0
1
1
1

 

4. y  ∈ H si y sólo si x + y + z = 0 y 2x − y − z = 0 si y solo si 
y  =   si y sólo si
 
0
2 −1 −1  
z
z
 


x
 
1
1
1
 
. Para calcular el espacio nulo de A aplicamos reducción Gauss-Jordan
y  ∈ N ul(A) con A = 
 
2 −1 −1
z


1
1
2 −1
1


−1
−2F1 +F2 →F2


1
1
0 −3
−F2 +F1 →F1


1


−3
1
0 0
0
1 1
−1
3 F2 →F2




1 1
0 1

1

1
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
81
   
 
0
x
x
   
 
   
 
Entonces y  ∈ N ul(A) si y sólo si x = 0 y y + z = 0 si y solo si x = 0 y y = −z si y sólo si y  = −z  =
   
 
z
z
z
  
 



0 
0


  
 
 
 
z −1. Por tanto H = gen −1 .

 
 




 1 
1
Terminamos el capı́tulo con con un teorema que será muy útil en el próximo capı́tulo.
Teorema 2.20. Sea A una matriz de tamaño m × n, entonces
1. N ul(A) = 0 si y sólo si rango(A) = n = # de columnas de A.
2. Col(A) = Rn si y sólo si rango(A) = m = # de filas de A.
Demostración.
1. N ul(A) = 0 si y sólo si la única solución a la ecuación Ax = 0 es x = 0 si y sólo si
rango(A) = n = # de columnas de A (Teorema 1.21.)
2. Col(A) = Rn si y sólo si b ∈ Col(A) para todo b ∈ Rn si y sólo si para todo b ∈ Rn , Ax = b si y sólo si la
ecuación Ax = b tiene solución para todo b ∈ Rn si y sólo si rango(A) = m = # de filas de A (Teorema
1.20.)
Problemas
2.8.1. Encuentre una base para cada uno de los siguientes subespacios:

 

 







 x x 




  
   
 
b. H = y  x = −t, y = 2t, z = −3t
a. H = y  3x − y = 0




 
 









 z

 z
2.9.
 





x
 









 y  


c. H =   x + y + z + w = 0



z 





 




 w

 



x


1


  
 ..  d. H =  .  a1 x1 + · · · + an xn = 0, an 6= 0


 




 x

n
El Teorema de la base incompleta en Rm
En el Corolario 2.6 se demostró que si v1 , . . . , vk son vectores linealmente independientes en Rm entonces
k ≤ m. El Teorema de la base incompleta dice que si k < m se pueden escoger vectores wk+1 , . . . , wm talque
v1 , . . . , vk , wk+1 , . . . , wm forman una base para Rm .
82
Teorema 2.21. (Teorema de la base incompleta) Sean v1 , . . . , vk vectores linealmente independientes en Rm .
Si k < m se pueden escoger vectores wk+1 , . . . , wm talque v1 , . . . , vk , wk+1 , . . . , wm forman una base para Rm .
h
i
Demostración. Sea A = v1 · · · vk la matriz cuyas columnas son los vectores v1 , . . . , vk , como estos son
linealmente independientes, entonces por el Teorema 2.5 tenemos que rango(A) = k y por tanto la forma
escalonada reducida A′ de A tiene un pivote en cada fila, luego A′ tiene la forma


1 ··· 0
.
.

. ..
. .. 
.


 h

i


0
·
·
·
1
 = e ··· e
A′ = 
1
k


0 · · · 0



. .
. . ... 
 ..


0
···
0
donde ei es el vector con un uno en la i-ésima componente y ceros en las demas componentes. Sean E1 , . . . , Es
matrices elementales talque
A′ = Es · · · E1 A
(2.8)
y sea B = E1−1 · · · Es−1 entonces tenemos lo siguiente
Afirmación 1. Las primeras k columnas de B son los vectores v1 , . . . , vk
Demostración de la afirmación: de la ecuación (2.8) se sigue que
h
A = E1−1 · · · Es−1 A′ = BA′ = B e1
|
{z
}
···
=B
i h
ek = Be1
···
Bek
i
como las columnas de A son los vectores v1 , · · · , vk entonces tenemos que Be1 = v1 , . . . , Bek = vk , luego
h
i
B = BI = B e1 · · · ek ek+1 · · · em
#
"
Be
·
·
·
Be
·
·
·
Be
Be
k+1
m
k
1
= |{z}
|{z}
vk
v1
h
= v1
···
vk
Bek+1
···
Bem
i
Afirmación 2. Las columnas de B son linealmente independientes.
Demostración de la afirmación: Como B es un producto de matrices invertibles, entonces B es invertible,
luego por el Corolario 1.22 tenemos que rango(A) = m entonces por el Teorema ?? los vectores son linealmente
independientes.
Ahora, como B tiene m columnas linealmente independientes, entonces estas forman una base para Rm , es
decir, los vectores v1 , . . . , vk , wk+1 , . . . , wm forman una base, donde wk+1 , . . . , wm son las últimas columnas de
B.
Este teorema exhibe un método computacional para completar una base, el cual escribimos a continuación:
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
83
Procedimiento 2.3. (Procedimiento para completar una base en Rm ) Sean v1 , . . . , vk vectores linealmente independientes en Rm con k < m, para calcular vectores wk+1 , . . . , wm talque los vectores v1 , . . . , vk , wk+1 , . . . , wm
forman una base, hacemos lo siguiente
h
1. Sea A = v1
i
vk la matriz formada con los vectores v1 , . . . , vk
···
2. Sea C el producto de las matrices elementales talque A = CA′ , esta matriz se calcula hallando la forma
h
i
h
i
escalonada reducida de la matriz A I ya que esta está dada por A′ C
3. Hacemos B = C −1
Si las columnas de B son linealmente independientes y por tanto forman una base para Rm y por el teorema
anterior, las primeras columnas de B son los vectores v1 , . . . , vk .
 
 
1
0
 
 
 
 
Ejemplo 2.17. (MatLab) Sean v1 = −1 y v2 = 1, calcular un vector v3 talque los vectores v1 , v2 , v3
 
 
2
1
3
forman una base para R .


0 1




Solución. Sea A = v1 v2 = −1 1, entonces hacemos lo siguiente


1 2
h
i
1. calculamos la forma escalonada reducida de la matriz A I usando MatLab
i
h
>> A = [01; −11; 12]; R=rref([A, eye(3)])
R=
1 0
0 −2/3
1/3
0 1
0
1/3
1/3
0 0 1 −1/3 −1/3
El producto de las matrices elementales es la matriz compuesta por las 3 últimas columnas de R, la cual
podemos definir usando MatLab como sigue
>> C = [R(:, 3), R(:, 4), R(:, 5)]
C=
0 −2/3
1/3
0
1/3
1/3
1 −1/3
−1/3
2. Ahora calculamos B = C −1 como sigue
B = inv(C)
B=
0
1
1
−1 1
0
1
2
0
84
Nótese que efectivamente
  las dos primeras columnas de esta matriz son los vectores v1 y v2 y por tanto los
1
 
 
vectores v1 , v2 y v3 = 0 forman una base para R3 .
 
0
Capı́tulo 3
Transformaciones Lineales
Carreta
3.1.
Definición y Ejemplos
En este capı́tulo se estudiarán funciones entre espacios vectoriales que preservan la estructura, estas funciones se llaman tranformaciones lineales, comenzamos con la definición.
Definición 3.1. Sean V y W espacios vectoriales y T : V −→ W una función, decimos que T es una transformación lineal si satisface:
1. T (v + v ′ ) = T (v) + T (v ′ ), para todo v, v ′ ∈ V .
2. T (αv) = αT (v), para todo v ∈ V y para todo α ∈ R.
Observación 3.1. Como consecuencia de la definición tenemos que si T : V −→ W es una transformación
lineal, v1 , . . . , vn ∈ V y α1 , . . . , αn ∈ R entonces
1. T (α1 v1 + α2 v2 ) = α1 T (v1 ) + α2 T (v2 ), y en general
2. T (α1 v1 + · · · + αn vn ) = α1 T (v1 ) + · · · + αn T (vn ).
Ejemplo 3.1.
1. Sean V y W espacios vectoriales sobre R. La función nula f : V W definida por f (v) = 0,
para todo v ∈ V y la función identidad Id : V −→ V definida por Id(v) = v son transformaciones lineales.
2. Si a ∈ R, entonces Ta : R → R dada por Ta (x) = ax para todo x ∈ R, es una transformación lineal. El
gráfico de Ta es una recta pasando por el origen (0, 0) ∈ R2 con pendiente a.
3. Sean a1 , · · · , an ∈ R. La función T : Rn → R definida por T (α1 , · · · , αn ) =
Pn
i=1
ai αi , es una transfor-
mación lineal tal que T (ei ) = ai , donde los ei denotan los elementos de la base canónica de Rn .
85
86
4. La función T : R2 −→ R definida por T (x, y) = x + y es una transformación lineal ya que
T ((x, y) + (x′ , y ′ )) = T (x + x′ , y + y ′ ) = x + x′ + y + y ′ = (x + y) + (x′ + y ′ ) = T (x, y) + T (x′ y ′ ) .
T (α(x, y)) = T (αx, αy) = αx + αy = α(x + y) = αT (x′ y ′ ) .
5. Si A es una matriz m × n, la función T : Rn −→ Rm definida por T (v) = Av es una transformación lineal
ya que satisface los axiomas 1 y 2 de la definición, más especı́ficamente tenemos que
T (v + w) = A(v + w) = Av + Aw = T (v) + T (w)
y
T (αv) = A(αv) = αAv = αT (v).
Destacamos las siguientes propiedades que cumple cualquier transformación lineal.
Teorema 3.1. Sean V y W espacios vectoriales y T : V −→ W una transformación lineal, entonces
1. T (0) = 0.
2. T (−v) = −T (v).
Demostración.
1. T (0) = T (0 + 0) = T (0) + T (0) por tanto T (0) = 0.
2. T (−v) = T ((−1)v) = −1T (v) = −T (v).
Por ahora nos concentraremos por ahora solo en transformaciones lineales de Rn en Rm , ya que éstas,
como se muestra en el siguiente teorema, son de la forma dada en el ı́tem 5 del Ejemplo 3.1, es decir, para
toda transformación lineal se puede encontrar una matriz A de tamaño m × n tal que T (x) = Ax. Pasamos a
enunciar el teorema.
Teorema 3.2. Sea T : Rn −→ Rm una transformación lineal, sea {e1 , . . . , en } la base estándar de Rn y
A = [T (e1 )
···
T (en )], la matriz cuyas columnas son los vectores T (e1 ), . . . , T (en ), entonces T (x) = Ax,
para todo x ∈ Rn . Más a’un, esta matriz es la única con la propiedad que T (x) = Ax.
 
α1
 
 .. 
Demostración. Sea x =  .  ∈ Rn , entonces x = α1 e1 + · · · + α1 en y tenemos lo siguiente
 
αn
T (x) = T (α1 e1 + · · · + α1 en ) = α1 T (e1 ) + · · · + α1 T (en )
 
α1
 
 .. 
= [T (e1 ) · · · T (en )]  .  = Ax.
{z
} 
|
=A
αn
87
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Ahora si B es una matriz tal que T (x) = Bx para todo x, entonces en particular los vectores de la base estándar
tenemos que
T (ei ) = Bei = i-ésima columna de B, para i = 1, . . . , n.
Pero T (ei ) es también la i-ésima columna de A, se sigue que B = A.
La matriz A en el teorema anterior depende de los vectores en la base estándar, la siguiente definición es
para hacer claridad respecto a esto.
Definición 3.2. Si T : Rn −→ Rm es una transformación lineal y E = {e1 , . . . , en } es la base estándar de
Rn , a la matriz A = [T (e1 )
A = E TE .
···
T (en )] se le llama la matriz de la transformación y será denotada por
 
x
Ejemplo 3.2. Calcular la matriz de la transformación T : R2 −→ R definida por T   = x + y.
y
Solución. De acuerdo al teorema anterior debemos calcular T (e1 ) y T (e2 ):
  
  
0
1
y
T (e2 ) = T   = 0 + 1 = 1.
T (e1 ) = T   = 1 + 0 = 1
1
0
Luego la matriz de la transformación es
E TE
= [1
1].
  


x
  
x
+
2y
  
.
Ejemplo 3.3. Calcular la matriz, E SE , de la transformación S : R3 −→ R2 definida por S y  = 
  
y − 3z
z
Solución. En este caso debemos calcular S(e1 ), S(e2 ) y S(e3 ).
  
 
  

  

1
0
  
 
  1 + 2 · 0 1
  0 + 2 · 1 2
S(e1 ) = S 0 =
, S(e2 ) = S 1 =
=
=
  
 
0
0−3·0
1
1−3·0
0
0
  
  

0
  
0
0
+
2
·
0
  
 =  .
y
S(e3 ) = S 0 = 
  
−3
0−3·1
1


1 2
0
.
Por tanto la matriz de la transformación es E SE = 
0 1 −3
En el siguiente teorema demostraremos que la composición de transformaciones lineales es una transforma-
ción lineal además veremos que la matriz de la transformación compuesta es el producto de las matrices de las
respectivas transformaciones.
Teorema 3.3. Sean V, W y Z espacios vectoriales y sean T : V −→ W y S : W −→ Z transformaciones
lineales, entonces S ◦ T es una transformación lineal. Más aún, si V = Rn , W = Rm y Z = Rq entonces la
matriz de la transformación S ◦ T está dada por
E SE ·E
TE , es decir,
E (S
◦ T ) E = E SE ·E T E .
88
Demostración. Primero demostremos que S ◦ T es una transformación lineal, sean v, v ′ ∈ V y α ∈ R,
S ◦ T (v + v ′ ) = S(T (v + v ′ )) = S(T (v) + T (v ′ )) = S(T (v)) + S(T (v ′ ))
= S ◦ T (v) + S ◦ T (v ′ )
y
S ◦ T (αv) = S(T (αv) = S(αT (v)) = αS(T (v)) = αS ◦ T (v)
Ahora demostremos la segunda parte, sean A =E TE y B =E SE , entonces T (v) = Av para todo v ∈ Rn y
S(w) = Bw para todo w ∈ Rm . Veamos que BA es la matriz de S ◦ T , es decir, S ◦ T (v) = BAv para todo
v ∈ Rn .
S ◦ T (v) = S(T (v)) = S(Av) = BAv.
De la propiedad de unicidad que satisface la matriz de S ◦ T concluimos que BA es la matriz de S ◦ T .
Ejemplo 3.4. Sean T y S las transformaciones lineales definidas en los Ejemplos 3.2 y 3.3 entonces la matriz
de la transformación T ◦ S,
E (T
◦ S)E , está dada por

i 1 2

E (T ◦ S)E =E TE ·E SE = 1 1
0 1
0

α1

   h
  
Por tanto T ◦ S α2  = 1 3
  
α3

α1

h
= 1 3
−3
h

i
−3 .
i 
 
−3 α2  = α1 + 3α2 − 3α3 .
 
α3
Ejemplo 3.5. (MatLab) Sean T : R3 −→ R4 y S : R4 −→ R3 las transformaciones lineales definidas por
T (x) = Ax y S(x) = Bx con
A=
3 2
1
1 1 1
2 0 −1
0 1 −2
yB=
Es fácil ver que si T (x) = Ax para todo x entonces A =
h
1 2 1 3
−1 2 1 0
2 0 −1 1
E TE
i
es la matriz de la transformación. Por tanto
obtenemos que las matrices de las compuestas T ◦ S y S ◦ T son las matrices AB y BA, respectivamente. Por
tanto T ◦ S(x) = ABx para todo x ∈ R4 y S ◦ T (y) = BAy para todo y ∈ R3 . Usando Matlab obtenemos que
3 10 4 10 h 7 7 −4 i
AB = 20 44 13 45 y BA = 1 0 0 .
4 5
−5 2 3 −2
1
Del Teorema 3.2 obtenemos que el conjunto de transformaciones lineales L(Rn , Rm ) de Rn en Rm está en
correspondencia uno a uno con el conjunto de matrices Mm,n (R)
L(Rn , Rm )
−→
Mm,n (R)
T
7→
A = E TE
T (x) = Ax
←
A
la correspondencia es tal que la composición de transformaciones se traduce en producto de matrices, también
veremos que la inversa de una transformación invertible se corresponde con la inversa de su matriz, la imagen
de la transformación con el espacio columna de la matriz y el kernel de la transformación (este se define en la
89
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
próxima sección) con el espacio nulo de la matriz. En general tendremos que la matriz de una transformación
se puede usar para conseguir información útil acerca de la transformación, por ejemplo, esta se puede usar para
determinar si una transformación lineal es inyectiva, si es sobre, si es biyectiva. Esto lo veremos en las secciones
3.2-3.4
Problemas
3.1.1. Determine si la función dada es una transformación lineal y en los casos afirmativos, calcule la matriz
de la transformación lineal correspondiente.

  
x
−
y
x
.
1. T : R2 −→ R2 definida por T   = 
x
y


 
x−y


x


2. T : R2 −→ R3 definida por T   = x + 1.


y
y2
 
x
  

 




x
−
y
y
  
.
3. T : R4 −→ R2 definida por T 
  =
 z 
zw
 
w

  
x−z
x

  

  
4. T : R3 −→ R3 definida por T y  = y − z .

  
x−z
z
 


x
 
x
−
z
 
.
5. T : R3 −→ R2 definida por T y  = 
 
y−z
z
6. T : Rn −→ Rn−1




x
 1  
  
definida por T · · · = 
  


xn
x1 − xn
x1 + x2 − xn
..
.




.



x1 + · · · + xn−1 − xn
 
 
  
 
  
2
1
 
 
−1
0
1
 
 
3.1.2. Sea T : R2 −→ R3 tal que T   = 2 y T   = 1. Calcule la matriz de T y T   .
 
 
1
1
0
2
2
3.1.3. Calcule la matriz de la transformación que rota el plano 90◦ y luego proyecta sobre el eje y.
3.1.4. Sea V = F([a, b], R el conjunto de las funciones continuas del intervalo [a,b] en R. Demuestre que la
Rb
función T : V → R definida por T (f ) = a f (x)dx es una transformación lineal.
90
3.1.5. Muestre que una función T : Rn → R es una transformación lineal si y solamente si existen a1 , · · · , an ∈
Pn
R tales que T (x1 , · · · , xn ) = i=1 ai xi .
3.1.6. Considere la función D : P3 −→ P2 definida por D(a + bt + ct2 + dt3 ) = b + 2ct + 3dt2 . Demuestre que
D es una transformación lineal.
En forma más general demuestre que la función D : Pn+1 −→ Pn definida por D(p(t)) = p′ (t) es una
transformación lineal.
3.1.7. Considere la función I : P2 −→ P3 definida por I(a + bt + ct2 ) = at + 21 bt2 + 13 ct3 . Demuestre que I es
una transformación lineal.
En forma más general demuestre que la función I : Pn −→ Pn+1 definida por D(p(t)) =
transformación lineal.
3.2.
Rt
0
p(x)dx es una
Transformaciones Lineales Inyectivas
En esta sección veremos que la inyectividad de una transformación lineal está ligada a con la nulidad de la
matriz de la transformación, y esto a su vez, depende de si kernel de la transformación es trivial. Comenzamos
con la definición de kernel de una transformación.
Definición 3.3. Sean V y W espacios vectoriales y sea T : V −→ W una transformación lineal, definimos el
núcleo o kernel de T como el conjunto
ker(T ) = {x ∈ V | T (x) = 0}.
Para transformaciones lineales de Rn en Rm , la matriz de la transformación se puede usar para calcular el
kernel. Este es el resultado del siguiente teorema.
Lema 3.4. Sea T : Rn −→ Rm una transformación lineal y sea A =
E TE
la matriz de la transformación,
entonces ker(T ) = N ul(A).
Demostración. x ∈ ker(T ) si y sólo si 0 = T (x) = Ax si y sólo si x ∈ N ul(A).
Concluimos que ker(T ) = N ul(A).
Ejemplo 3.6. Calculemos el kernel de la transformación
lineal S

 definida en el Ejemplo 3.3.
1 2
0
, necesitamos calcular N ul(A), para lo cual
Solución. La matriz de la transformación es A = 
0 1 −3
necesitamos la escalonada reducida de A:


1 2
0 1
0


−3
F1 − 2F2 → F1


1 0
0 1
6

.
−3
91
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
 
x
 
x = −6z
 
.
Luego tenemos que un vector v = y  ∈ N ul(A) = N ul(A′ ) si y sólo si se satisfacen las ecuaciones
 
y = 3z
z
 

  
 
−6
−6z
x
x
 

  
 
 

  
 
Entonces tenemos que v = y  ∈ N ul(A) si y sólo si y  =  3z  = z  3 .
 

  
 
1
z
z
z
  




−6


 
Por tanto tenemos que ker(T ) = N ul(A) = gen  3  .

 




 1 
El siguiente resultado muestra la relación entre la inyectividad de una transformación lineal y la trivialidad
del kernel.
Teorema 3.5. Sea T : V −→ W una transformación lineal, entonces T es inyectiva si y sólo si ker(T ) = {0}.
Demostración. “⇒”Supongamos que T es inyectiva, entonces si T (v) = T (w), tenemos que v = w.
Ahora, supongamos que v ∈ ker(T ), entonces T (v) = 0 = T (0), luego v = 0 y por tanto ker(T ) ⊆ {0}. La
otra inclusión se da ya que ker(T ) es un subespacio de V y por tanto 0 ∈ ker(T ). Concluimos que ker(T ) = {0}.
“⇐”Supongamos que ker(T ) = {0} y demostremos que si T (v) = T (w), entonces v = w, para todo v, w ∈ V .
Supongamos entonces que T (v) = T (w). Luego T (v − w) = T (v) + T (−w) = T (v) − T (w) = 0, se sigue que
v − w ∈ ker(T ) = {0} por tanto v − w = 0 o equivalentemente v = w. Concluimos que T es inyectiva.
En el caso particular de transformaciones lineales que van de Rn en Rm , el Teorema 3.5 y el Lema 3.4 nos
dan un algoritmo para calcular el kernel, este se hace evidente con el siguiente resultado.
Teorema 3.6. Sea T : Rn −→ Rm una transformación lineal y sea A =
E TE
la matriz de la transformación.
Entonces T es inyectiva si y sólo si rango(A) = n = número de columnas de A.
Demostración. T es inyectiva si y sólo si ker(T ) = {0} (Teorema 3.5) si y sólo si N ul(A) = {0} (Lema 3.4) si
y sólo si rango(A) = n (Teorema 2.16).
Este teorema nos da una manera de determinar si una transformación lineal es inyectiva y en caso negativo,
usamos el Lema 3.4 para calcularlo. A continuación damos los siguientes ejemplos.
  


x
  
x
+
2y




 es
Ejemplo 3.7. Determine si la transformación lineal T : R3 −→ R2 definida por T y  = 
  
y − 3z
z
inyectiva.


Solución. En el Ejemplo 3.6 vimos que la matriz de la transformación es A = 

escalonada reducida de A es A′ = 
de A, por tanto A no es inyectiva.
1 0
6
0 1 −3

1 2
0 1
0
 y la forma
−3
. De esto deducimos que rango(A) = 2 < número de columnas
92

1
−2
3
4





2
3 −4 5
 y sea T : R4 −→ R4 la transformación lineal definida

Ejemplo 3.8. (MatLab) Sea A = 

3
4
5 6


4
5
6 7
por T (v) = Av. Determine si T es inyectiva y calcular su kernel.
Solución. Como la matriz de la transformación es la única para la cual T (v) = Av, tenemos que A = E TE es
la matriz de la tranformación, para determinar si T es o no inyectiva, necesitamos calcular el rango de A, lo
cual calculamos como sigue en MatLab:
>> A = [1, −2, 3, 4; 2, 3, −4, 5; 3, 4, 5, 6; 4, 5, 6, 7]; rank(A)
y ası́ se obtiene que rango(A) = 4 = número de columnas de A y se sigue que T es inyectiva y ker(T ) = {0}.


−1 −2
1
1 1




 1
0
1 −3 1




Ejemplo 3.9. (MatLab) Sea A =  0
1 −1
1 1 y sea T : R5 −→ R5 definida por T (x) = Ax,




 0
1 −1
1 1


1
0
1 −3 1
determine si T es inyectiva y calcular ker(T ).
Solución. Primero calculamos el rango de A para determinar si la transformación es inyectiva,
>> A = [−1, −2, 1, 1, 1; 1, 0, 1, −3, 1; 0, 1, −1, 1, 1; 0, 1, −1, 1, 1; 1, 0, 1, −3, 1]; rank(A)
y obtenemos que rango(A) = 3 y por tanto T no inyectiva. Para calcular el kernel, computamos el subespacio
nulo de A.
>> null(A,′ r′ )
    



−1  3 





  








1
−1 

    

   
Obtenemos que ker(T ) = N ul(A) = gen  1  ,  0  .

   


   



 0   1 













 0
0 
Problemas
3.2.1. Calcular el kernel de las transformaciones lineales del Problema 3.1.1.
3.2.2. Determine cuatro transformaciones lineales de R3 en R3 cuyos núcleos tengan dimensiones 0, 1, 2 y 3
respectivamente.
3.2.3. Sea T : Rn −→ Rm una transformación lineal. Demuestre que si T es inyectiva entonces n ≤ m.
3.2.4. Sea T : Rn −→ Rm una transformación lineal y A = E TE la matriz de T . Demuestre que T es inyectiva
si y sólo si A tiene inversa a la izquierda.
3.2.5. Demuestre que si T : U −→ V y S : V −→ W son inyectivas entonces S ◦ T es inyectiva, es decir, la
composición de transformaciones inyectivas es inyectiva.
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
93
3.2.6. Sean A y B matrices de tamaños m × n y n × p, respectivamente. Demuestre que si A y B tienen ambas
inversa a la izquierda entonces AB tiene inversa a la izquierda. (Ayuda: Use los dos últimos problemas.)
3.2.7. Demuestre que si T : Rn −→ Rm es inyectiva entonces existe una transformación lineal S : Rm −→ Rn
tal que S ◦ T = id. (Ayuda: Use el Problema 3.2.4.)
3.3.
Transformaciones Lineales Sobreyectivas
Comenzamos recordando las definiciones de imagen de una función y de función sobreyectiva.
Definición 3.4. Sean V y W espacios vectoriales y T : V −→ W una transformación lineal,
1. Definimos la imagen de T , denotada por Im(T ), como el conjunto
Im(T ) = {T (v) | v ∈ V } = {w ∈ W | existe v ∈ V tal que w = T (v)}.
2. Decimos que T es sobreyectiva si Im(T ) = W .
Cuando la transformación está definida de Rn en Rm podemos calcular la imagen usando la matriz de la
transformación. Este hecho se demuestra en el siguiente teorema.
Teorema 3.7. Sean T : Rn −→ Rm una transformación lineal y A = E TE la matriz de T , entonces
Im(T ) = Col(A).
Demostración. Sean A1 , . . . , An las columnas de A entonces tenemos lo siguiente:
..
.
w ∈ Im(T ) si y sólo si existe v ∈ Rn tal que w = T (v) = Av si y sólo si existe v = (α1

α1
 
 . 
αn ) ∈ Rn tal que w = Av = [A1 , . . . , An ]  ..  = α1 A1 + · · · + αn An si y sólo si w ∈ gen{A1 , . . . , An } = Col(A).
 
αn
Por tanto Im(T ) = Col(A).


1
0




Ejemplo 3.10. Sea A = 1 −2 y T : R2 −→ R3 la transformación lineal definida por T (x) = Ax, calcular


3
0
la imagen de T .

Solución. De acuerdo al teorema anterior necesitamos calcular

 Col(A).
1 0




Si calculamos la forma escalonada de A obtenemos A′ = 0 1 y por tanto por el Teorema 2.16


0 0
    



0 
1


    
   
Im(T ) = Col(A) = gen 1 , −2 .

   




 3
0 
94
El teorema anterior nos muestra como la matriz de la transformación se puede usar para calcular la imagen de
una transformación, ésta también sirve para determinar si la transformación es sobreyectiva, esto lo mostramos
a continuación.
Teorema 3.8. Sea T : Rn −→ Rm una transformación lineal y A la matriz de T , entonces T es sobreyectiva si
y sólo si rango(A) = m = número de filas de A.
Demostración. T es sobre si y sólo si Rm = Im(T ) = Col(A) (Teorema 3.7) y Col(A) = Rm si y sólo si
rango(A) = m = número de filas de A (Teorema 2.16).
El Teorema 3.7 nos dice que encontrar la imagen de una transformación es equivalente a encontrar el
espacio columna de la matriz de la transformación y el teorema anterior reduce el problema de determinar si la
transformación es sobre a encontrar el rango de esta matriz. Esto lo ilustramos en los siguientes ejemplos.
Ejemplo 3.11. Determine si la transformación del ejemplo
 anterior
 es sobreyectiva.
1 0




Solución. La forma escalonada de la matriz de T es A′ = 0 1 y por tanto rango(A) = 2 < 3 = número de


0 0
filas de A, concluimos que T no es sobreyectiva.
Ejemplo 3.12. (MatLab) Sea T la transformación del Ejemplo 3.9, determine si T es sobre y calcular Im(T ).
Solución. En el Ejemplo 3.9 se obtuvo que el rango de la matriz A =E TE es 3 y por tanto T no es sobre.
Para calcular Im(T ) necesitamos calcular el espacio columna de A, el cual podemos calcular con la escalonada
reducida de A.
′
>> A = [−1, −2, 1, 1,1; 1, 0, 1, −3, 1; 0, 1, 
−1, 1, 1; 0, 1, −1, 1, 1; 1, 0,
1,

 (A)
 rref
 −3,1];A =

 −1

1 0
1 −3 0
1 
−2





     

      







0 1 −1






1 0
1
0
1

      











se obtiene que A′ 0 0
0
0 1 y por tanto Im(T ) =  0  ,  1  , 1 , es decir, ImT es gene


     

      





0 0

 0   1  1
0
0 0





     




 1
0 0
0
0 0
1 
0
rada por la primera, segunda y quinta columna de A.
Otra forma de calcular la imagen es usando el comando colspace(sym(A)), el cual produce una base de
Col(A) = Im(T ).
>> A = [−1, −2, 1, 1, 1; 1, 0, 1, −3, 1; 0, 1, −1, 1, 1;
0,1, 
−1,1,1; 1,
1, −3, 1]; colspace(sym(A))

 0,

 1


0
0


     



     











0
1
0


      
     
y de esta manera obtenemos que el conjunto 0 , 0 , 1 es una base para Im(T ).

     



     



0 0 1














 0
0 
1
Problemas
95
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
3.3.1. Sea T : R2 −→ R2 definida por T (x, y) = (y, 0), muestre que ker T = ImT .
3.3.2. Calcular la imagen de las transformaciones lineales del Problema 3.1.1.
3.3.3. Sean V y W los subespacios de R4 determinados por V = gen {(1, 0, 1, 1), (0, −1, −1, −1)} y W =
(x, y, z, t) ∈ R4 : x + y = 0 y t + z = 0 . Determine una transformación lineal T : R4 → R4 tal que ker(T ) =
V y Im(T ) = W .
3.3.4. Encuentre una transformación lineal T : R4 → R4 tal que: ker(T ) = gen {(1, 0, 1, 0), (−1, 0, 0, 1)} y
Im(T ) = {(1, −1, 0, 2), (0, 1, −1, 0)}.
3.3.5. Sea V un espacio vectorial y T : V → V una transformación lineal. Demuestre que las siguientes
condiciones son equivalentes:
1. ker(T ) ∩ Im(T ) = {0}.
2. Si (T ◦ T )(v) = 0 para v ∈ V , entonces T (v) = 0.
3.3.6. Sean A ∈ Mn (R) y T : Rn −→ Rn definida por T (v) = Av, sea T k = |T ◦ ·{z
· · ◦ T} y Ck = Col(Ak ),
k−veces
demuestre que para todo k ≥ 1 se tiene que
1. Ck = Col(Ak ).
2. T (Ck ) = Ck+1 , donde T (Ck ) = {T (v) | v ∈ Ck }.
3.3.7. Sean T : U −→ V y S : V −→ W transformaciones lineales sobreyectivas. Demuestre que S◦ es
sobreyectiva.
3.3.8. Sea T : Rn −→ Rm una transformación lineal y A = E TE la matriz de T . Demuestre que T es sobreyectiva
si y sólo si A tiene inversa a la derecha.
3.3.9. Demuestre que si T : Rn −→ Rm es sobreyectiva entonces existe una transformación lineal S : Rm −→ Rn
tal que T ◦ S = id y muestre que S es inyectiva.
3.3.10. Sean A y B matrices de tamaños m × n y n × p, respectivamente. Demuestre que si A y B tienen ambas
inversa a la derecha entonces AB tiene inversa a la derecha. (Ayuda: Use los dos últimos problemas.)
3.3.11. Demuestre que si T : Rn −→ Rm es sobreyectiva entonces n ≥ m.
3.3.12. Si T : V −→ V es una transformación lineal y H ⊆ V es un subespacio, decimos que H es T -invariante
si T (H) ⊆ H. Muestre que ImT y ker T son T -invariantes.
3.3.13. Si T : V −→ V es una transformación lineal y W ⊆ V es un subespacio T -invariante muestre que
T/W : W −→ W es una transformación lineal, donde T/W es la restricción de T a W .
96
3.3.14. Sea T : V −→ W una transformación lineal y H ⊆ W un subespacio. La imagen inversa de H se define
como el conjunto
T −1 (H) = {v ∈ V | T (v) ∈ H}.
Muestre que T −1 (H) es un subespacio.
3.3.15. Si T : V −→ W y S : W −→ Z son transformaciones lineales con S sobreyectiva entonces Im(T ) =
Im(T oS). (Ayuda:Use el Problema 2.7.14.)
3.3.16. Sean T, S : V −→ V transformaciones lineales, demuestre que Im(T + S) ⊆ ImT + ImS, donde
T +S : V −→ V es la transformación lineal definida por (T +S)(v) = T (v)+S(v), y concluya que rango(A+B) ≤
rangoA + rangoB.
3.4.
Isomorfismos
Las transformaciones lineales biyectivas (inyectivas y sobreyectivas) se llaman isomorfismos, la palabra isomorfismo significa igual forma, en este sentido se usa el término isomorfismo para las transformaciones que
preservan la estructura de espacio vectorial. En esta sección veremos como los isomorfismos preservan la estructura de los espacios vectoriales. Comenzamos con la definición de isomorfismo.
Definición 3.5. Sean V y W espacios vectoriales y T : V −→ W una transformación lineal, decimos que
T es un isomorfismo si es una función biyectiva. También diremos que V es isomorfo a W si existe un
isomorfismo entre ellos, lo cual denotaremos V ∼
= W.
Los Teoremas 3.6 y 3.8 implican lo siguiente.
Teorema 3.9. Sea T : Rn −→ Rm una transformación lineal y A =E TE la matriz de T , entonces T es un
isomorfismo si y sólo si rango(A) = m = n.
Corolario 3.10. Rn ∼
= Rm si y sólo si m = n.

Ejemplo 3.13. Sea T : R2 −→ R2 la tranformación lineal cuya matriz es A = 
un isomorfismo.
1
1

, determinar si T es
1 −1
Solución. La forma escalonada reducida de A es la matriz A′ = I, por tanto T es un isomorfismo.
Teorema 3.11. Sea T : Rn −→ Rn una transformación lineal y A = E TE la matriz de T , entonces su función
inversa T −1 es una transformación lineal y su matriz de transformación es A−1 .
Demostración. Primero veamos que T −1 es lineal. Sean y1 , y2 ∈ Rn , como T es sobre, existen x1 , x2 ∈ Rn tal
que y1 = T (x1 ) y y2 = T (x2 ), entonces
T −1 (y1 + y2 ) = T −1 (T (x1 ) + T (x2 )) = T −1 (T (x1 + x2 )) = x1 + x2
= T −1 (y1 ) + T −1 (y2 ).
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
97
Ahora, sea α ∈ R, entonces tenemos
T −1 (αy1 ) = T −1 (αT (x1 )) = T −1 (T (αx1 )) = αx1 = αT −1 (y1 ).
Por tanto T −1 es lineal. Ahora veamos que A−1 es la matriz de transformación de T . Nótese que si y ∈ Rn
entonces y = AA−1 y = T (A−1 y), aplicando T −1 a ambos lados obtenemos
T −1 (y) = A−1 y.
Conluimos que A−1 es la matriz de T −1 .
Observación 3.2. En general si T : V −→ W es un isomorfismo, entonces T −1 : W −→ V también es una
transformación lineal.
2
2
Ejemplo
3.14.
matriz es

 −→ R cuya
 En el ejemplo anterior vimos que la transformación lineal T : R

1/2
1/2
1
1
 . Es decir, la
 es invertible, entonces T −1 es un isomorfismo y su matriz es A−1 = 
A=
1/2 −1/2
1 −1
   

1
x
(x
+
y)
.
transformación está dada por T   =  2
1
y
2 (x − y)
Hasta ahora la mayorı́a de los teoremas que hemos visto en el capı́tulo y en el anterior aplican solamente al
espacio vectorial Rn y a transformaciones lineales de Rn en Rm . Vamos a usar la teorı́a de isomorfismos para
generalizar los teoremas vistos, comenzamos con un resultado que nos va a servir de puente para extender estos
teoremas.
Teorema 3.12. Sea V un espacio vectorial y X = {v1 , . . . , vn } una base para V , entonces V ∼
= Rn . Un
isomorfismo entre estos espacios está dado por la función T : V −→ Rn definida por T (α1 v1 + · · · + αn vn ) =
 
α1
 
 .. 
 .  , a esta función se le conoce como el isomorfismo canónico.
 
αn
Demostración. Veamos que T es un isomorfismo.
T es lineal: Sean v, w ∈ V y α ∈ R, como {v1 , . . . , vn } es una base para V , existen α1 , . . . , αn , β1 . . . , βn ∈ R tal
que v = α1 v1 + · · · + αn vn y w = β1 v1 + · · · + βn vn , luego
T (v + w) = T (α1 v1 + · · · + αn vn + β1 v1 + · · · + βn vn )
= T ((α1 + β1 )v1 + · · · + (αn + βn ))
    

β1
α1
α1 + β1
    

..
  ..   .. 

=
= . + . 
.
    

βn
αn
αn + βn
= T (α1 v1 + · · · + αn vn ) + T (β1 v1 + · · · + βn vn )
= T (v) + T (w).
98
T (αv) = T (α(α1 v1 + · · · + αn vn ))
= T (αα1 v1 + · · · + ααn vn )
 


α1
αα1
 


 .. 
 .. 
=  .  = α . 
 


αn
ααn
= αT (α1 v1 + · · · + αn vn )
= αT (v).
T es inyectiva: Para esto veamos que ker(T ) = {0}.

α1
 
 . 
“⊆”Sea v = α1 v1 + · · · + αn vn ∈ ker(T ), entonces 0 = T (v) =  .. . Entonces α1 = · · · = αn = 0 y por
 
αn
tanto v = 0.

La otra inclusión es inmediata ya que T (0) = 0 y por tanto 0 ∈ ker(T ).
 
α1
 
 .. 
T es sobreyectiva: Sea y =  .  ∈ Rn , y sea v = α1 v1 + · · · + αn vn ∈ V , entonces tenemos que
 
αn
 
α1
 
 .. 
T (v) = T (α1 v1 + · · · + αn vn ) =  .  = y.
 
αn
Por tanto T es sobreyectiva.
Concluimos que T es un isomorfismo.
Observación 3.3. Nótese que en el teorema anterior la transformación T depende de la base X, más aún, por
cada base de V tenemos un isomorfismo distinto. Debido a la dependencia de la base, en adelante denotaremos
a esta transformación por RX .
Ejemplo 3.15. El conjunto X = {1, t, t2 , t3 } es una base del espacio V = P3 , por tanto V es isomorfo a R4 y
el isomorfismo está dado por
 
a
 0
 
a1 

RX (a0 + a1 t + a2 t2 + a3 t3 ) = 
 .
a2 
 
a3
El número de vectores en una base es invariante, este hecho se demostró en el Capı́tulo 2 Teorema 2.15 pero
sólo en el caso de subespacios de Rn , a continuación lo demostramos para espacios vectoriales en general.
Teorema 3.13. Sea V un espacio vectorial y sean X = {v1 , . . . , vn } y Y = {w1 , . . . , wm } bases para V, entonces
m = n.
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
99
Demostración. Por el teorema anterior tenemos que V ∼
= Rm , luego Rn ∼
= Rm . Luego por el
= Rn y V ∼
Corolario 3.10 tenemos que m = n.
Esto nos permite definir la dimensión de espacios vectoriales, al tener que el número de vectores en una base
es invariante.
Definición 3.6. Sea V un espacio vectorial, definimos la dimensión de V, denotada por dim V , como el número
de vectores en una base de V. Es decir, si {v1 , . . . , vn } es una base para V entonces dim V = n.
1. Como el conjunto {1, t, . . . , tn } es una base para Pn , tenemos que dim Pn = n + 1.


 
 
 
 1 0
0 0 
0 0
0 1
 , por tanto dim M22 (R) = 4.
,
,
,
2. Una base para M22 (R) está dada por 
 0 0
0 1 
1 0
0 0
Ejemplo 3.16.
3. En general tenemos que dim Mmn (R) = mn. Una base para este espacio está dada por {eij | i =
1, . . . , n, j = 1, . . . , m}, donde eij es la matriz m × n con un 1 en la posición ij y cero en las demás
posiciones.
El siguiente teorema muestra como los isomorfismo conservan la estructura de los espacios vectoriales, en
otras palabras, el siguiente teorema justifica por que las transformaciones biyectivas son llamadas isomorfismos.
Teorema 3.14. Sean V y W espacios vectoriales, T : V −→ W un isomorfismo, {v1 , . . . , vn } ⊆ V y v ∈ V .
Entonces se tiene lo siguiente:
1. El conjunto {v1 , . . . , vn } es linealmente independiente si y sólo si el conjunto {T (v1 ), . . . , T (vn )} es linealmente independiente.
2. El conjunto {v1 , . . . , vn } genera a V si y sólo si el conjunto {T (v1 ), . . . , T (vn )} genera a W .
3. El conjunto {v1 , . . . , vn } es una base para V si y sólo si el conjunto {T (v1 ), . . . , T (vn )} es una base para
W.
4. dim V = dim W .
5. v ∈ gen{v1 , . . . , vn } si y sólo si T (v) ∈ gen{T (v1 ), . . . , T (vn )}.
Demostración.
1. “⇒”Supongamos que el conjunto {v1 , . . . , vn } es linealmente independiente y suponga-
mos que α1 T (v1 ) + · · · + αn T (vn ) = 0. Entonces 0 = T (0) = T (α1 v1 + · · · + αn vn ). Como T es inyectiva,
tenemos que α1 v1 + · · · + αn vn = 0. Ahora, como {v1 , . . . , vn } es linealmente independiente, tenemos que
α1 = · · · = αn = 0. De aquı́ concluimos que {T (v1 ), . . . , T (vn )} es linealmente independiente.
“⇐”Supongamos que {T (v1 ), . . . , T (vn )} es linealmente independiente y supongamos que α1 v1 + · · · +
αn vn = 0. Entonces tenemos que 0 = T (0) = T (α1 v1 + · · · + αn vn ) = α1 T (v1 ) + · · · + αn T (vn ). Como
{T (v1 ), . . . , T (vn )} es linealmente independiente tenemos que α1 = · · · = αn = 0. Por tanto {v1 , . . . , vn }
es linealmente independiente.
100
2. Como T es un isomorfismo, es en particular inyectivo y sobreyectivo, por tanto ker(T ) = {0} y W = Im(T ).
Entonces tenemos lo siguiente:
{T (v1 ), . . . , T (vn )} genera a W si y sólo si {T (v1 ), . . . , T (vn )} genera a Im(T ) si y sólo si para todo v ∈ V
existen constantes α1 , . . . , αn tal que T (v) = α1 T (v1 ) + · · · + αn T (vn ) si y sólo si para todo v ∈ V existen
constantes α1 , . . . , αn tal que T (v) = T (α1 v1 + · · · + αn vn ) si y sólo si para todo v ∈ V existen constantes
α1 , . . . , αn tal que 0 = T (α1 v1 + · · · + αn vn ) − T (v) = T (α1 v1 + · · · + αn vn − v) si y sólo si para todo
v ∈ V existen constantes α1 , . . . , αn tal que α1 v1 + · · · + αn vn − v ∈ ker(T ) = {0} si y sólo si para todo
v ∈ V existen constantes α1 , . . . , αn tal que α1 v1 + · · · + αn vn − v = 0 si y sólo si para todo v ∈ V existen
constantes α1 , . . . , αn tal que v = α1 v1 + · · · + αn vn si y sólo si {v1 , . . . , vn } genera a V .
3. Es inmediato de 1 y 2.
4. Es inmediato de 3
5. v ∈ gen{v1 , . . . , vn } si y sólo si existen constantes α1 , . . . , αn tal que v = α1 v1 + · · · + αn vn si y sólo si
existen constantes α1 , . . . , αn tal que T (v) = T (α1 v1 + · · · + αn vn ) = α1 T (v1 ) + · · · + αn T (vn ) si y sólo si
T (v) ∈ gen{T (v1 ), . . . , T (vn )}.
En la próxima sección explotaremos toda la potencia de los Teoremas 3.6 y 3.14, lo cual nos permitirá estudiar
independencia lineal, conjuntos generadores y bases en espacios vectoriales arbitrarios. También nos ayudará a
estudiar inyectividad, sobreyectividad y biyectividad de transformaciones lineales entre espacios vectoriales arbitrarios.
Problemas



 1 a 
 a ∈ R el espacio vectorial con suma definida por A ⊕ B = AB donde AB denota
3.4.1. Sea V = 
 0 1





1 αa
1 a
 . Demuestre que
 = 
el producto usual de matrices y el producto por escalar definido por α · 
0 1
0 1
V ∼
= R exhibiendo un isomorfismo entre estos espacios.
3.4.2. Muestre que las siguientes transformaciones lineales de R3 en R3 son invertibles y determine su transformación lineal inversa.
1. T (x, y, z) = (x − 3y − 2z, y − 4z, −z).
2. T (x, y, z) = (x, x − y, 2x + y − z).
3.4.3. Sea T : R2 → R2 dada por T (x1 , x2 ) = (x1 + x2 , x1 ) para todo (x1 , x2 ) ∈ R2 . Demuestre que T es un
isomorfismo y determine T −1 .
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
101
3.4.4. Sea V un espacio vectorial y S, T : V → V transformaciones lineales invertibles. Demuestre que S ◦ T
es invertible y (S ◦ T )−1 = T −1 ◦ S −1 .
3.4.5. Sean T : R3 → R2 y S : R2 → R3 transformaciones lineales. Demuestre que S ◦ T no es invertible.
De un ejemplo donde T ◦ S es invertible.
3.4.6. Sea A ∈ Mn (R) y T : Mn (R) −→ Mn (R) la función definida por T (X) = AX. Muestre que T es una
transformación lineal y muestre que T es invertible si y sólo si A es invertible.
3.4.7. Sea T : V −→ V un transformación lineal, Ck = Im(T k ) y Nk = ker(T k ), demuestre lo siguiente:
1. Ck+1 ⊆ Ck ,
2. T (Ck ) = Ck+1 . (Recuerde que para H ⊆ V se define T (H) como el conjunto T (H) = {T (h) | h ∈ H},)
3. Nk ⊆ Nk+1 ,
4. T (Nk ) ⊆ Nk ,
3.4.8. Si T : V −→ W y S : W −→ V son transformaciones lineales muestre que
1. Im(S ◦ T ) ⊆ Im(S),
2. Si T admite una inversa a la derecha entonces Im(S ◦ T ) = Im(S).
3.5.
Espacios Vectoriales Arbitrarios
En esta sección veremos como los Teoremas 3.6 y 3.14 nos permiten resolver las preguntas sobre independencia
lineal, conjuntos generadores y bases en espacios vectoriales arbitrarios con un procedimiento Gauss-Jordan.
Ejemplo 3.17. Considere los polinomios p1 = 1 − 2t2 , p2 = t + t2 − t3 y p3 = t + 3t2 en P3 . Determinar si los
polinomios son linealmente independientes.
 
a
 0
 
 a1 

Solución. Por el Teorema 3.6 la función T = RX : P3 −→ R4 determinada por T (a0 +a1 t+a2 t2 +a3 t3 ) = 
 
 a2 
 
a3
es un isomorfismo. Entonces por
3.14 tenemos
{p
1 , p2 , p3 } es linealmente indepen el Teorema
 
 que
 el conjunto
 



1
0
0 


 
 
 



 
 
 


 0
 1
1
 , T (p2 ) =   , T (p3 ) =   es linealmente independiente.
diente si y sólo si el conjunto T (p1 ) = 
 
 
 


−2
 1
3







 





0
−1
0 


1
0 0




 0
1 1

Sabemos por el Teorema 2.5 que este último conjunto es LI si la matriz [T (p1 ) T (p2 ) T (p3 )] = 


−2
1 3


0 −1 0
102
tiene rango igual al número de columnas. Aplicando

1 0


0 1
calonada reducida de esta matriz es la matriz 

0 0

0 0
tanto los polinomios {p1 , p2 , p3 } son LI.
el procedimiento
Gauss-Jordan obtenemos que la forma es
0


0
. Luego los vectores {T (p1 ), T (p2 ), T (p3 )} son LI y por

1

0







−5 1
0 3
0
1
−2
, determine
 y M4 = 
 , M3 = 
 , M2 = 
Ejemplo 3.18. (MatLab) Sean M1 = 
−5 3
1 0
1 −1
0
0
si las matrices son LI en M22 (R) y si no lo son encontrar una dependencia lineal entre ellos.

1
4
Solución. El procedimiento es análogo
  al ejemplo anterior. Por el Teorema 3.6 la función T : M22 (R) −→ R
a
 


 
b
a c
 =   es un isomorfismo. Entonces el conjunto {M1 , M2 , M3 , M4 } es linealdeterminada por T 
 
c
b d
 
d
mente
independiente
si
y
sólo
si
el
conjunto

 
 
 
 



1
0
0
−5 

 

 
 
 


 

 
 
 


 0
 1
1
−5
 , T (M2 ) =   , T (M3 ) =   , T (M4 ) =   es linealmente independiente. Al calcular
T (M1 ) = 
 
 
 
 


−2
 1
3
 1 









 





0
−1
0
3 


1 0 0 −5






0
1
0
−3
, por
la forma escalonada de la matriz A = [T (M1 ) T (M2 ) T (M3 ) T (M4 )] obtenemos A′ = 


0 0 1 −2


0 0 0
0
tanto los vectores no son LI y tenemos que T (M4 ) = −5T (M1 ) − 3T (M2 ) − 2T (M1 ), como T es un isomorfismo
tenemos que M4 = −5M1 − 3M2 − 2M3 , lo que nos da una dependencia lineal entre las matrices M1 , M2 , M3 y
M4 .
Ejemplo 3.19. Sean M1 , M2 , M3 y M4 las matrices
del
 ejemplo anterior, calcular una base y la dimensión de

1 1
 ∈ H.
H = gen{M1 , M2 , M3 , M4 } y determine si M = 
1 3
Solución. De acuerdo al ejemplo anterior sabemos que M1 , M2 y M3 son LI y que M4 es una combinación
lineal de estas, por tanto {M1 , M2 , M3 } es una base para H y dim(H) = 3.
Para determinar si M ∈ H, usamos el Teorema 3.14 el cual dice que M ∈ H si y sólo si T (M ) ∈ T (H) si y
sólo si existen constantes α1 , α2 , α3 tal que T (M ) = α1 T (M1 ) + α2 T (M2 ) + α3 T (M3 ) si y sólo si el conjunto
{T (M1 ), T (M2 ), T (M3 ), T (M )} es LD.
103
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Esto lo podemos saber calculando la forma escalonada reducida de la matriz

1
0 0


 0
1 1
A = [T (M1 ) T (M2 ) T (M3 ) T (M )] = 

−2
1 3

0 −1 0
1



1
.

1

3
Después de hacer los respectivos cálculos podemos notar que A′ = I y por tanto los vectores son LI. Concluimos
que T (M ) ∈
/ T (H), luego M ∈
/ H.
Problemas
3.5.1. Encuentre una base para {p ∈ R3 [x] | p(−1) = 0}.
3.5.1.
Transformaciones lineales entre espacios vectoriales arbitrarios.
En esta sección definiremos la matriz de una transformación con respecto a una base del dominio y otra del
codominio. Esto nos permitirá calcular el kernel y la imagen de una transformación lineal de manera computacional. La matriz de la transformación con respecto a dos bases dadas nos permitirá ver una transformación lineal
entre espacios arbitrarios como una transformación de Rn en Rm . En las siguientes observaciones introducimos
la matriz de una transformación con respecto a dos bases.
Observación 3.4. Sean V y W espacios vectoriales, sean X = {v1 , . . . , vn } y Y = {w1 , . . . , wm } bases de V
y W respectivamente y T : V → W una transformación lineal. Por el Teorema 3.12 tenemos los isomorfismos
canónicos RX : V −→ Rn y RY : W −→ Rm definidos por
RX (α1 v1 + · · · + αn vn ) = (α1 , . . . , αn )
y
RY (β1 w1 + · · · + βm vm ) = (β1 , . . . , βm ).
Por tanto tenemos el siguiente diagrama:
T
V
/W
RY
RX
Rn
S
/ Rm ,
−1
ası́ se obtiene una transformación lineal S : Rn −→ Rm , la cual está dada por S = RY ◦ T ◦ RX
.
Esta transformación tiene asociada una matriz
E SS
la cual nos permitirá calcular el kernel y la imagen de
T.
Teorema 3.15. Usando la notación de la Observación 3.4. Sean V y W espacios vectoriales, X = {v1 , . . . , vn }
una base para V , Y = {w1 , . . . , wm } una base para W y T : V −→ W una transformación lineal. Entonces
tenemos lo siguiente:
104
1. S es inyectiva si y sólo si T es inyectiva.
2. S es sobreyectiva si y sólo si T es sobreyectiva.
3. S es un isomorfismo si y sólo si T es un isomorfismo.
Demostración. Por la definición de S tenemos que T = RY−1 ◦S ◦RX , además como RX y RY son isomorfismos,
son en particular inyectivos y sobreyectivos.
1. “⇒”Si S es inyectiva entonces T = RY−1 ◦ S ◦ RX es una composición de transformaciones inyectivas y por tanto
es T inyectiva.
−1
“⇐”Si T es inyectiva entonces S = RY ◦ T ◦ RX
es una composición de transformaciones inyectivas y por tanto
S es inyectiva.
2. “⇒”Si S es sobreyetiva entonces T = RY−1 ◦ S ◦ RX es una composición de transformaciones sobreyectivas y por
tanto es T sobreyectiva.
−1
es una composición de transformaciones sobreyectivas y
“⇐”Si T es sobreyectiva entonces S = RY ◦ T ◦ RX
por tanto S es sobreyectiva.
3. Se sigue de 1. y 2.
Este teorema nos permite asociar a cualquier transformación lineal entre espacios vectoriales arbitrarios
una transformación lineal de Rn en Rm que respeta la inyectividad, la sobreyectividad y le biyectividad de la
transformación, de éste se deduce los siguientes resultados que nos dicen como determinar si la transformación
es inyectiva y/o sobreyectiva, también como calcular el kernel y la imagen.
Corolario 3.16. Usando la notación de la Observación 3.4. Sean V y W espacios vectoriales, X = {v1 , . . . , vn }
una base para V , Y = {w1 , . . . , wm } una base para W , T : V −→ W una transformación lineal, S = Rn −→ Rm
y A = E SE la matriz de la transformación S. Entonces
1. T es inyectiva si y sólo si rango(A) = número de columnas de A.
2. T es sobreyectiva si y sólo si rango(A) = número de filas de A.
3. T es un isomorfismo si y sólo si rango(A) = número de filas de A = número de columnas de A.
Demostración. Esto es una consecuencia inmediata del teorema anterior y los Teoremas 3.6, 3.8 y 3.9.
Corolario 3.17. Sean V y W espacios vectoriales, sea X = {v1 , . . . , vn } una base para V , Y = {w1 , . . . , wm }
una base para W , T : V −→ W una transformación lineal. RX : V −→ Rn y RY : W −→ Rm los isomorfismos
−1
canónicos de V y W , respectivamente, sea S = RY ◦ T ◦ RX
: Rn −→ Rm y sea A =
transformación S. Entonces tenemos lo siguiente:
−1
−1
1. ker(T ) = RX
(ker(S)) = RX
(N ul(A)).
E SE
la matriz de la
105
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
2. Im(T ) = RY−1 (Im(S)) = RY−1 (Col(A)).
Además se sigue que
−1
−1
{x1 , . . . , xr } es una base de N ul(A) si y sólo si {RX
(x1 ), . . . , RX
(xr )} es una base de ker(T ) y
{y1 , . . . , ys } es una base de Col(A) si y sólo si {RY−1 (y1 ), . . . , RY−1 (ys )} es una base de Im(T ).
Demostración.
1.
v ∈ ker(T ) si y sólo si
0 = T (v) = RY−1 ◦ S ◦ RX (v)
si y sólo si
RX (v) ∈ ker(S) = N ul(A)
si y sólo si
−1
v ∈ RX
(N ul(A)).
si y sólo si
S ◦ RX (v) = 0
2.
w ∈ Im(T ) si y sólo si existe v ∈ V tal que w = T (v) = RY−1 ◦ S ◦ RX (v)
si y sólo si existe v ∈ V tal que RY (w) = S(RX (v))
si y sólo si RY (w) ∈ Im(S) = Col(A)
si y sólo si w ∈ RY−1 (Col(A)).
A continuación daremos ejemplos de como usar estos corolarios para calcular la imagen y el kernel de
transformaciones lineales.
Ejemplo 3.20. Considere la transformación lineal derivación D : P3 −→ P2 definida en el Problema 3.1.6.
Determinar si es inyectiva y/o sobreyectiva, si es un isomorfismo, calcular el kernel y la imagen de D.
Solución. Los conjuntos X = {1, t, t2 , t3 } y Y = {1, t, t2 } son bases de P2 y P3 , respectivamente. Se tienen los
isomorfismos RX : P3 −→ R4 y RY : P2 −→ R3 definidos por RX (a0 + a1 t + a2 t2 + a3 t3 ) = (a0 , a1 , a2 , a3 ) y
RY (a0 + a1 t + a2 t2 ) = (a0 , a1 , a2 ) (Los isomorfismos canónicos de P3 y P2 , respectivamente).
−1
La transformación S = RY ◦ D ◦ RX
: R4 −→ R3 está dada por
−1
S(a, b, c, d) = RY ◦ D ◦ RX
(a, b, c, d) = RY ◦ D(a + bt + ct2 + dt3 ) = RY (b + 2ct + 3dt2 ) = (b, 2c, 3d)
La matriz de esta transformación es
A =E SE = [S(e1 )

S(e2 )
0 1
S(e3 )
0 0


0 1


S(e4 )] = 0 0

0 0
0 0



2 0

0 3




y su forma escalonada está dada por A′ = 0 0 1 0. Por tanto la transformación S es sobreyectiva pero no


0 0 0 1
inyectiva. Del Teorema 3.15 tenemos que D es sobreyectiva pero no inyectiva, por tanto no es un isomorfismo.
106
Ahora pasamos a calcular el kernel y la imagen. Como D es sobre entonces Im(D) = P2 . Para el kernel,
−1
usamos el Corolario 3.17, el cual nos dice que si calculamos una base de N ul(A) y aplicamos RX
obtenemos
una base de ker(D).
Nótese que
 
   
 
1
α1
α1
α1
 
   
 
 
   
 
0
α   0 
α2 
  ∈ N ul(A′ ) = N ul(A) si y sólo si α2 = α3 = α4 = 0 si y sólo si  2  =   = α1   .
 
   
 
0
α3   0 
α3 
 
   
 
0
0
α4
α4
  



1 

 








 0  
−1


(x1 ) = 1} una base para ker(D).
Se sigue que x1 =   es una base de N ul(A) = ker(S). Por tanto {RX

 0  





  


 0 
Es decir
ker(D) = gen{1} = { polinomios constantes }.
Ejemplo 3.21. Considere la transformación lineal integración I : P2 −→ P3 definida en el Problema 3.1.7.
Determinar si I es inyectiva y/o sobreyectiva, si es un isomorfismo, calcular el kernel y la imagen de I.
Solución. Nuevamente consideramos las bases del problema anterior Y = {1, t, t2 } y X = {1, t, t2 , t3 } y los
isomorfismos RX : P3 −→ R4 definido por RX (a0 + a1 t+ a2 t2 + a3 t3 ) = (a0 , a1 , a2 , a3 ) y RY : P2 −→ R3 definido
por RY (a0 + a1 t + a2 t2 ) = (a0 , a1 , a2 ).
En este caso la transformación S = RX ◦ I ◦ RY−1 : R3 −→ R4 está dada por
b 2 c 3
b c
−1
2
S(a, b, c) = RX ◦ I ◦ RY (a, b, c) = RX ◦ I(a + bt + ct ) = RX at + t + t = a, ,
2
3
2 3
La matriz de esta transformación es

0
0
0





1
0
0 


A =E SE = [S(e1 ) S(e2 ) S(e3 )] = 

0 1/2
0 


0
0
1/3


1 0 0






0
1
0
. Por tanto la transformación S es inyectiva pero
y su forma escalonada reducida está dada por A′ = 


0 0 1


0 0 0
no sobreyectiva, luego por el Teorema 3.15 tenemos que I es inyectiva pero no sobreyectiva, por tanto no es un
isomorfismo.
Ahora pasamos a calcular el kernel y la imagen. Como I es inyectiva entonces ker(I) = {0}. Para calcular
−1
la imagen, usamos el Corolario 3.17, el cual no dice que si calculamos una base de Col(A) y aplicamos RX
obtenemos una base de Im(I).
107
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
De la matriz A′ obtenemos que una base para Col(A) = Im(I) está dada por el conjunto
0
0 0 0
1
y1 = 0 , y2 = 1/2 , y3 = 00
,
0
1/3
0
−1
−1
−1
ya que A′ tiene pivotes en las tres columnas. Por tanto el conjunto {RX
(y1 ), RX
(y2 ), RX
(y3 )} = t, 12 t2 , 13 t3
es una base para Im(I). Es decir
1 2 1 3
Im(I) = gen t, t , t = gen{t, t2 , t3 }.
2 3


1 −1
 y sea T : M22 (R) −→ M22 (R) la función definida por T (A) = AM .
Ejemplo 3.22. Sea M = 
−1
1
Demuestre que T es una transformación lineal, determine si T es inyectiva y/o sobreyectiva, si es un isomorfismo
y calcular el kernel y la imagen de T .
Solución. Primero veamos que T es una transformación lineal. Sean A1 , A2 ∈ M22 (R) y α ∈ R,
T (A1 + A2 ) = (A1 + A2 )M = A1 M + A2 M = T (A1 ) + T (A2 )
y
T (αA1 ) = (αA1 )M = α(A1 M ) = αT (A1 ).
Fijemos la base
X=



E11





0
0 0
1 0
 , E12 = 
 , E21 = 
=
0
1 0
0 0

0 

2 


0
1
 , E22 = 
0
0
y consideremos el isomorfismo RX : M22 −→ R4 definido por


a c
 = RX (aE11 + bE21 + cE12 + dE22 ) = (a, b, c, d).
R X 
b d
−1
La transformación S = RX ◦ T ◦ RX
: R4 −→ R4 está dada por

−1
S (a, b, c, d) = RX ◦ T ◦ RX
(a, b, c, d) = RX ◦ T 

= R X 
La matriz de esta transformación es
a−c
−a + c
b−d
−b + d
a
c
b
d



  = R X 
a
c
b
d


 M
 = (a − c, b − d, −a + c, −b + d).

1
0
−1
0





 0
1
0 −1

A = E SE = [S(e1 ) S(e2 ) S(e3 ) S(e4 )] = 


−1
0
1
0


0 −1
0
1


1 0 −1
0






0
1
0
−1
. Luego S no es inyectiva ni sobreyectiva y
y su forma escalonada reducida es la matriz A′ = 


0 0
0
0


0 0
0
0
tampoco un isomorfismo.
108
′
 De lamatriz
 que una base para Col(A) está dada por las dos primeras columnas de A, es decir,
 A tenemos



0 
1


 
 










 1 
 0
 , m2 =   es una base para Col(A) = Im(S). Por tanto se tiene que una base para Im(T )
m1 = 
 
 

 0 
−1




 







−1 
0
está dada por


 

 1 −1
0
0
−1
−1
 .
,
{RX
(m1 ), RX
(m2 )} = 
 0
1 −1 
0
Ahora para calcular ker(T ) necesitamos una base para N ul(A). Para esto nótese que

α1

 
 
α2 
α = α3
  ∈ N ul(A) = N ul(A′ ) si y sólo si 1
 
α3 
α2 = α4
 
α4




 
 
1
0
   
 
 
   
 
 
α2  α4 
 0
1
  
 
 
si y sólo si 
  =   = α3   + α4   .
α3  α3 
 1
0
   
 
 
α4
α4
0
1
α1
α3
 
 

0 
1

 
 

 
 
 1 
 0




Se sigue que el conjunto x1 =   , x2 =   es una base para N ul(A) = ker(S). Por tanto el conjunto


 0 
 1




 
 





1 
0









 1
−1
−1
(x2 )} = 
(x1 ), RX
{RX
 0
es una base para ker(T ).
 
0
1
,
1
0

0 
 ,
1 

1
 y sea T : M22 (R) −→ M22 (R) la función definida por T (B) = M B. Demuestre
Ejemplo 3.23. Sea M = 
1 1
que T es una transformación lineal, determine si T es inyectiva y/o sobre, si es un isomorfismo y calcular el

2
kernel y la imagen de T .
Solución. Con un argumento similar al del ejemplo anterior se demuestra que T es una transformación lineal.
Para los demás cálculos fijemos la base de M22 (R)
X=



E11




0
0 0
1 0
 , E12 = 
 , E21 = 
=
0
1 0
0 0

y tomemos el isomorfismo RX : M22 −→ R4 definido por

R X 
a
c
b
d



0
1
 , E22 = 
0
0

0 

2 
 = RX (aE11 + bE21 + cE12 + dE22 ) = (a, b, c, d).
109
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
−1
En este caso la transformación S = RX ◦ T ◦ RX
: R4 −→ R4 está dada por


 
a
a c
−1
  = R X M 
S(a, b, c, d) = RX ◦ T ◦ RX (a, b, c, d) = RX ◦ T 
b
b d


2a + b 2c + d
 = (2a + b, a + b, 2c + d, c + d).
= RX 
a+b
c+d
c
d


La matriz de esta transformación es

A=
E SE
= [S(e1 )
S(e2 )

S(e3 )
1 0


0 1
y su forma escalonada reducida es la matriz A′ = 

0 0

0 0
sobreyectiva y por tanto es un isomorfismo.
2 1


1 1
S(e4 )] = 

0 0

0 0
0 0

0 0



0 0


2 1

1 1


0 0
 = I. De esto concluimos que S es inyectiva y

1 0

0 1
Como T es un isomorfismo tenemos que ker(T ) = {0} y Im(T ) = M22 (R).
Problemas
3.5.2. Calcule la matriz de la tranformación T : R3 [t] −→ R3 [t] definida por T (p) =
d
dt [(2
+ t)p].
3.5.3. Sean V un espacio vectorial de dimensión finita y T : V → V una transformación lineal. Suponga que
existe S : V → V tal que T ◦ S = IdV . Demuestre que T es invertible y S = T −1 . De un ejemplo que muestre
que lo anterior es falso cuando V no es de dimensión finita.
3.5.4. Sea T : U → V una transformación lineal inyectiva. Muestre que V tiene un subespacio isomorfo a U .
Sea T : V −→ V una transformación lineal y X una base de V , demuestre que T : V −→ V es invertible si y
sólo si la matriz
X TX
es invertible.
3.5.5. Sea V un espacio vectorial con dim V ≥ 3. Muestre que una función T : V → V es una transformación
lineal si y sólo la restricción de T a cada subespacio vectorial de V con dimensión 2 es una transformación
lineal.
3.5.6. Si T : V −→ W y S : W −→ Z son transformaciones lineales entonces Im(T ◦S) ⊆ Im(T ) y Im(T ◦S) ⊆
Im(S).
3.5.7. Si T, S : V −→ V son transformaciones lineales y T ◦ S es invertible entonces T y S son invertibles.
De un ejemplo en el que T : V −→ W y S : W −→ V con T ◦ S invertible pero ni T ni S son invertibles.
110
3.5.8. Sea T : Mn (R) −→ Mn (R) definida por T (A) = A − At . Demuestre que ker T = Sn(R) es el conjunto de
marices simétricas y la imagen Im(T ) = An (R) es el conjunto de matrices antisimétricas.
3.5.9. Si T : V −→ W y S : W −→ V son transformaciones lineales con dim V > dim W entonces S ◦ T no es
invertible.
3.6.
Propiedades de los Espacios Vectoriales
En esta sección estudiaremos resultados clásicos de espacios vectoriales, como el Teorema de la Base Incompleta y los teoremas de la dimensión, entre otros. Comenzamos con el siguiente resultado que garantiza que la
representación de un vector en términos de una base es única salvo el orden.
Teorema 3.18. Sea V un espacio vectorial, {v1 , . . . , vn } una base de V y v ∈ V , entonces existen constantes
únicas α1 , . . . , αn talque v = α1 v1 + · · · + αn vn .
Demostración. Supongamos que existen constantes α1 , . . . , αn talque v = α1 v1 + · · · + αn vn y supongamos
que existen otras constantes β1 , . . . , βn tal que v = β1 v1 + · · · + βn vn . Entonces restando estas dos ecuaciones
obtenemos:
0 = v − v = α1 v1 + · · · + αn vn − (β1 v1 + · · · + βn vn ) = (α1 − β1 )v1 + · · · + (α1 − βn )vn
luego, como los vectores v1 , . . . , vn son LI, entonces 0 = α1 −β1 = · · · = αn −βn , por tanto α1 = β1 , . . . , αn = βn
y las constantes son únicas.
Los siguientes resultados son generalizaciones de los Teoremas 2.11 ı́tem 2. y 2.16 que se enunciaron y se
demotraron en el Capı́tulo 2.
Teorema 3.19. Sea V un espacio vectorial y sea {v1 , . . . , vn } un conjunto linealmente independiente. Si
dim(V ) = n entonces {v1 , . . . , vn } es una base para V.
Demostración. Como dim(V ) = n entonces V tiene una base X con n elementos, aplicando el Teorema 3.12
existe un isomorfismo T = RX : V −→ Rn y por el Teorema 3.14 ı́tem 1 el conjunto {T (v1 ), . . . , T (vn )} es
linealmente independiente en Rn , luego por el Teorema 2.11 ı́tem 2, este conjunto forma una base para Rn .
Aplicando nuevamente el Teorema 3.14 ı́tem 1 tenemos que {v1 , . . . , vn } es una base de V .
Teorema 3.20. Sean V y W espacios vectoriales con dim(V ) = n y sea T : V −→ W una transformación
lineal. Entonces
dim(ker T ) + dim(ImT ) = n.
Demostración. Sea m = dim(W ), sean X y Y bases de V y W respectivamente, y sean RX : V −→ Rn y
−1
RY : W −→ Rm los isomorfismos canónicos de V y W , respectivamente. Definamos S = RY ◦ T ◦ RX
y sea
A = E SE la matriz de transformación de S, entonces por el Corolario 2.17 tenemos que
dim(N ulA) + dim(ColA) = n.
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
111
Ahora por el Corolario 3.17, se tiene que dim(ImT ) = dim(ImS) = dim(ColA) y dim(KerT ) = dim(KerS) =
dim(N ulA) entonces tenemos
dim(ImT ) + dim(KerT ) = dim(ImS) + dim(N ulS) = dim(ColA) + dim(N ulA) = n.
Ahora pasamos a demostrar el teorema de la base incompleta en su versión general, para facilitar su demostración veamos el siguiente lema.
Lema 3.21. Sea V un espacio vectorial, {v1 , . . . , vk } ⊆ V un conjunto de vectores linealmente independientes
y w ∈ V . Si w ∈
/ gen{v1 , . . . , vk } entonces el conjunto {v1 , . . . , vk , w} es linealmente independiente.
Demostración. Supongamos que w ∈
/ gen{v1 , . . . , vk }. Para demostrar que {v1 , . . . , vk , w} es linealmente
independiente, supongamos que
α1 v1 + · · · + αk vk + βw = 0
(3.1)
y veamos que las constantes son todas cero.
Primero nótese que β = 0, ya que si β 6= 0, entonces de la Ecuación 3.1 tenemos que w = − αβ1 v1 − · · · − αβk vk
y por tanto w ∈ gen{v1 , . . . , vk } lo que contradice la hipótesis, por tanto β = 0.
Entonces la Ecuación 3.1 se reduce a α1 v1 + · · · + αk vk = 0. Pero por hipótesis {v1 , . . . , vk } es un conjunto
LI, se sigue por tanto que 0 = α1 = · · · = αk .
De esto concluimos que {v1 , . . . , vk , w} es linealmente independiente.
Teorema 3.22. (Teorema de la Base Incompleta) Sean V un espacio vectorial con dim(V ) = n, {v1 , . . . , vk }
un conjunto de vectores linealmente independientes con k < n. Entonces existen vectores vk+1 , . . . , vn tal que
{v1 , . . . , vk , vk+1 , . . . , vn } es una base para V .
Demostración. Como {v1 , . . . , vk } es linealmente independiente, entonces dim gen{v1 , . . . , vk } = k y como
k < n entonces gen{v1 , . . . , vk } =
6 V , por tanto existe v ∈ V tal que v ∈
/ gen{v1 , . . . , vk }, entonces aplicando el
lema anterior tenemos que {v1 , . . . , vk , v} es LI.
Tomemos vk+1 = v y ası́ tenemos que {v1 , . . . , vk , vk+1 } es linealmente independiente. Si n = k + 1 entonces
V = gen{v1 , . . . , vk , vk+1 } y por tanto {v1 , . . . , vk , vk+1 } es una base de V . En el caso k + 1 < n tenemos que
gen{v1 , . . . , vk , vk+1 } 6= V y existe w ∈ V tal que w ∈
/ gen{v1 , . . . , vk , vk+1 }, entonces aplicando de nuevo el
lema anterior tenemos que {v1 , . . . , vk , vk+1 , w} es linealmente independiente.
Hacemos vk+2 = w y tenemos que {v1 , . . . , vk , vk+1 , vk+2 } es linealmente independiente.
Continuando de manera inductiva conseguimos vectores vk+1 , . . . , vn tal que {v1 , . . . , vk , vk+1 , . . . , vn } es
linealmente independiente, entonces como dim(V ) = n, por el Teorema 3.19 tenemos que
{v1 , . . . , vk , vk+1 , . . . , vn } es una base para V .
Teorema 3.23. Sea V un espacio vectorial y sean W1 y W2 subespacios de V . Entonces
dim(W1 + W2 ) = dim(W1 ) + dim(W2 ) − dim(W1 ∩ W2 ).
112
Demostración. Sea n = dim(V ), r = dim(W1 ), s = dim(W2 ) y t = dim(W1 ∩ W2 ). Sea {w1 , . . . , wt } una base
para W1 ∩W2 , por el Teorema de la Base Incompleta, existen vectores xt+1 , . . . , xr tal que {w1 , . . . , wt , xt+1 , . . . , xr }
es una base para W1 y existen vectores yt+1 , . . . , ys tal que {w1 , . . . , wt , yt+1 , . . . , ys } es una base para W2 .
Afirmación 1: El conjunto {w1 , . . . , wt , xt+1 , . . . , xr , yt+1 , . . . , ys } es linealmente independiente.
Para demostrar esta afirmación, supongamos que
α1 w1 + · · · + αt wt + βt+1 xt+1 + · · · + βr xr + λt+1 yt+1 + · · · + λs ys = 0.
(3.2)
Sea v = λt+1 yt+1 + · · · + λs ys ∈ W2 , entonces por la Ecuación 3.2 tenemos que
v = λt+1 yt+1 + · · · + λs ys = −α1 w1 − · · · − αt wt − βt+1 xt+1 − · · · + βr xr ∈ W1
por tanto v ∈ W1 ∩ W2 , entonces existen constantes σ1 , . . . , σt tal que v = σ1 w1 + · · · + σt wt . Se sigue que
0 = v − v = σ1 w1 + · · · + σt wt − λt+1 yt+1 − · · · − λs ys ,
pero como {w1 , . . . , wt , yt+1 , . . . , ys } es linealmente independiente, por ser base de W2 , entonces
0 = σ 1 = · · · = σ t = λ1 = · · · = λs .
Entonces la Ecuación 3.2 se reduce a α1 w1 + · · · + αt wt + βt+1 xt+1 + · · · + βr xr = 0, pero el conjunto
{w1 , . . . , wt , xt+1 , . . . , xr } es linealmente independiente, por ser base de W1 , entonces
0 = α 1 = · · · = αt = β1 = · · · = βs .
Concluimos que {w1 , . . . , wt , xt+1 , . . . , xr , yt+1 , . . . , ys } es linealmente independiente, lo que demuestra la Afirmación 1.
Afirmación 2: El conjunto {w1 , . . . , wt , xt+1 , . . . , xr , yt+1 , . . . , ys } genera a W1 + W2 .
Tomemos w ∈ W1 + W2 , entonces existen x ∈ W1 y y ∈ W2 tal que w = x + y.
Como {w1 , . . . , wt , xt+1 , . . . , xr } es una base para W1 , existen constantes α1 , . . . , αr tal que
x = α1 w1 + · · · + αt wt + αt+1 xt+1 + · · · + αr xr .
(3.3)
Similarmente existen constantes β1 , . . . , βs tal que
y = β1 w1 + · · · + βt wt + βt+1 yt+1 + · · · + βs ys .
De las Ecuaciones 3.3 y 3.4 tenemos que
w =x + y
=α1 w1 + · · · + αt wt + αt+1 xt+1 + · · · + αr xr
+ β1 w1 + · · · + βt wt + βt+1 yt+1 + · · · + βs ys
=(α1 + β1 )w1 + · · · + (αt + βt )wt + αt+1 xt+1 + · · · + αr xr + βt+1 yt+1 + · · · + βs ys .
(3.4)
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
113
Lo que demuestra la Afirmación 2.
De las Afirmaciones 1. y 2. tenemos que el conjunto {w1 , . . . , wt , xt+1 , . . . , xr , yt+1 , . . . , ys } es una base para
W1 + W2 . Por tanto
dim(W1 + W2 ) = t + r − t + s − t = r + s − t = dim(W1 ) + dim(W2 ) − dim(W1 ∩ W2 ).
Problemas
3.6.1. Sea V un espacio vectorial de dimensión n.
1. Si n es impar, demuestre que no existe ninguna transformación lineal T : V −→ V tal que ker(T ) = Im(T ).
2. Exhiba un contraejemplo a la afirmación anterior si n es par.
3.6.2. Muestre que si T : V → W es una transformación lineal inyectiva, entonces dim V ≤ dim W .
3.6.3. Considere una transformación lineal T : V −→ W , donde V y W son espacios vectoriales de dimensión
finita tales que dim W < dim V .
1. Demuestre que existe un elemento no nulo v ∈ V talque T (v) = 0.
2. Si X es una base arbitraria de V , ¿existe un vector v ∈ X tal que T (v) = 0? Demuestre o de un contra ejemplo.
3.6.4. Sea T : V −→ V una transformación lineal demuestre que las siguientes afirmaciones son equivalentes
1. T es invertible
2. T es inyectiva
3. T es sobreyectiva
3.6.5. El problema anterior no es cierto en dimensión infinta, muestre que la transformación lineal T : R[t] −→
Rt
R[t] definida por T (p) = 0 p(x)dx es inyectiva pero no sobre y la transformación T : R[t] −→ R[t] definida por
T (p) = p′ es sobre pero no inyectiva.
Los dos siguientes problemas bosquejan otra forma de demostrar el Teorema 3.20
3.6.6. Sean V y W espacios vectoriales, T : V −→ W una transformación lineal y {v1 , . . . , vt } una base de ker T .
Si vt+1 , . . . , vn son vectores tal que {v1 , . . . , vt , vt+1 , . . . , vn } es una base de V entonces {T (vt+1 ), . . . , T (vn )} es
una base de Im(T ).
3.6.7. Sean V y W espacios vectoriales, T : V −→ W una transformación lineal y {w1 , . . . , wt } una base de
Im(T ) y sean v1 , . . . , vt vectores tal que wi = T (vi ), para i = 1, . . . , t. Demuestre lo siguiente
1. El conjunto {v1 , . . . , vt } es linealmente independiente.
114
2. Si vt+1 , . . . , vn son vectores tal que {v1 , . . . , vt , vt+1 , . . . , vn } es una base de V entonces {vt+1 , . . . , vn } es una
base de ker(T ).
3.6.8. Muestre que la función
tr :
Mn (R)
−→
R
es una TL sobreyectiva con ker tr = sln (R) = {A ∈
A
7→ tr(A)
Mn (R) | trA = 0}. Use esto y el Teorema de la Dimensión para transformaciones lineales para determinar
dim sln (R).
3.7.
Suma Directa de Espacios
Terminamos el capı́tulo con la definición de suma directa y las propiedades más relevantes.
Definición 3.7. (Suma Directa) Sean V un espacio vectorial y W1 y W2 subespacios de V , decimos que V
es la suma directa de W1 y W2 , lo cual denotamos por V = W1 ⊕ W2 , si V = W1 + W2 y W1 ∩ W2 = {0}.
Los siguientes resultados exhiben condiciones suficientes y necesarias para que un espacio sea suma directa
de dos subespacios.
Teorema 3.24. Sean V un espacio vectorial y W1 y W2 subespacios de V . Entonces V = W1 ⊕ W2 si y sólo si
V = W1 + W2 y dim W1 + dim W2 = dim V .
Demostración. “⇒”Si V = W1 ⊕ W2 entonces por definición tenemos que V = W1 + W2 y por el Teorema de
la dimensión (Teorema ??) tenemos que
dim V = dim W1 + dim W2 − dim(W1 ∩ W2 ) = dim W1 + dim W2 .
|
{z
}
=0
“⇐”Si V = W1 + W2 y dim W1 + dim W2 = dim V por el Teorema de la dimensión tenemos que
dim V = dim W1 + dim W2 − dim(W1 ∩ W2 ),
se sigue que dim(W1 ∩ W2 ) = 0 y por tanto V = W1 ⊕ W2 .
Teorema 3.25. Sean V un espacio vectorial, W1 y W2 subespacios de V y X y Y bases para W1 y W2 ,
respectivamente. Entonces V = W1 ⊕ W2 si y sólo si X ∪ Y es una base para V .
Demostración. “⇒”Supongamos que V = W1 ⊕ W2 y sean X = {v1 , . . . , vr } y Y = {w1 , . . . , ws } bases de W1
y W2 . Veamos que {v1 , . . . , vr , w1 , . . . , ws } es LI.
Supongamos que
α1 v 1 + · · · + αr v r + β1 w1 + · · · + βs ws = 0
(3.5)
y definamos x = α1 v1 + · · · + αr vr entonces x ∈ W1 y de (3.5) se sigue que x = α1 v1 + · · · + αr vr = −(β1 w1 +
· · · + βs ws ) y por tanto x ∈ W2 . Se sigue que x ∈ W1 ∩ W2 pero por hipótesis W1 ∩ W2 = {0}, luego x = 0 y
como x = α1 v1 + · · · + αr vr y {v1 , . . . , vr } es LI por ser base para W1 tenemos que α1 = · · · = αr = 0. Además
como −(β1 w1 + · · · + βs ws ) = x = 0 y {w1 , . . . , ws } es LI entonces 0 = β1 = · · · = βs .
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
115
Concluimos que X ∪ Y = {v1 , . . . , vr , w1 , . . . , ws } es LI. Ahora, por el teorema anterior dim V = dim W1 +
dim W2 = r + s entonces X ∪ Y es un conjunto LI con r + s = dim V elementos y por tanto es una base de V .
“⇐”Supongamos que X ∪ Y = {v1 , . . . , vr , w1 , . . . , ws } es una base para V .
Afirmación 1. V = W1 + W2
Demostración. Sea v ∈ V , como {v1 , . . . , vr , w1 , . . . , ws } es una base para V , existen constantes α1 , . . . , αr , β1 , . . . , βs
tal que
v = α1 v1 + · · · + αr vr + β1 w1 + · · · + βs ws ∈ W1 + W2 .
{z
} |
|
{z
}
∈W1
∈W2
La otra inclusión es clara ya que como W1 y W2 son subespacios entonces W1 + W2 es un subespacio, en
particular es un subconjunto. Esto demuestra la afirmación.
Afirmación 2. W1 ∩ W2 = {0}.
Demostración. Sea v ∈ W1 ∩ W2 , entonces v ∈ W1 y v ∈ W2 . Como {v1 , . . . , vr } es una base de W1 , existen
constantes α1 , . . . , αr tal que
v = α1 v 1 + · · · + αr v r .
(3.6)
Un argumento similar garantiza la existencia de constantes β1 , . . . , βs tal que
v = β1 v 1 + · · · + βr v r .
(3.7)
De las ecuaciones 3.6 y 3.7 tenemos que
0 = v − v = α 1 v 1 + · · · + αr v r − β1 w1 + · · · + βs ws .
Ahora, como {v1 , . . . , vr , w1 , . . . , ws } es linealmente independiente, por ser base para V , tenemos que 0 = α1 =
· · · = αr = β1 = · · · = βs . Por tanto v = α1 v1 + · · · + αr vr = 0 y W1 ∩ W2 ⊆ {0}. La otra inclusión es trivial ya
que 0 ∈ W1 + W2 luego {0} ⊆ W1 ∩ W2 . Lo que prueba la afirmación.
De las afirmaciones 1. y 2. tenemos que V = W1 ⊕ W2 .
Terminamos la sección con una última caracterización de la suma directa de espacios vectoriales.
Teorema 3.26. Sea V un espacio vectorial, sean W1 y W2 subespacios de V . Entonces V = W1 ⊕ W2 si y sólo
si para todo v ∈ V existen vectores únicos w1 ∈ W1 y w2 ∈ W2 tal que v = w1 + w2 .
Demostración. “⇒”: Supongamos que V = W1 ⊕ W2 , entonces por definición tenemos que V = W1 + W2 ,
por tanto para v ∈ V existen w1 ∈ W1 y w2 ∈ W2 tal que v = w1 + w2 .
Ahora veamos que estos vectores son únicos: supongamos que v = w1 +w2 y que v = w1′ +w2′ con w1 , w1′ ∈ W1
y w2 , w2′ ∈ W2 . Entonces tenemos que
0 = v − v = (w1 − w1′ ) + (w2 − w2′ )
se sigue que w1 − w1′ = w2′ − w2 ∈ W2 , pero como w1 , w1′ ∈ W1 tenemos que w1 − w1′ ∈ W1 y por tanto
w1 − w1′ ∈ W1 ∩ W2 = {0}, obtenemos que w1 − w1′ = 0 o equivalentemente w1 = w1′ . Similarmente se demuestra
que w2 = w2′ .
116
“⇐”: Supongamos que para todo v ∈ V existen vectores únicos w1 ∈ W1 y w2 ∈ W2 tal que v = w1 + w2 .
Se sigue que V = W1 + W2 , ahora veamos que W1 ∩ W2 = {0}.
Sea x ∈ W1 ∩ W2 , entonces x = 0 + x ∈ W1 + W2 y x = x + 0 ∈ W1 + W2 , como la expresión es única se
sigue que x = 0.
Problemas
3.7.1. Demuestre que si T : V −→ V es una transformación lineal tal que T ◦ T = T entonces V = Im(T ) ⊕
ker(T ).
3.7.2. Exhiba un ejemplo de una transformación lineal T : V −→ V tal que ker(T ) ∩ Im(T ) 6= {0}.
3.7.3. Sean W1 y W2 subespacios de un espacio vectorial V , demuestre que V = W1 ⊕ W2 si y sólo si dim W1 +
dim W2 = dim V y W1 ∩ W2 = {0}.
3.7.4. Demuestre que R2 = gen{(1, 0)} ⊕ gen{(1, 1)}.
3.7.5. Demuestre que el espacio de matrices n × n es la suma directa del subespacio de matrices simétricas y el
subespacio de matrices antisimétricas, es decir, Mn (R) ∼
= Sn (R) ⊕ An (R). (Ayuda: Use el Ejercicio 1.2.11).
3.7.6. Sean V = F(R, R) el conjunto de las funciones f de R en R, W1 = {f ∈ V : f (x) = f (−x), ∀x ∈ R} y
W2 = {f ∈ V : f (−x) = −f (x), ∀x ∈ R}. Demuestre que W1 y W2 son subespacios de V y que V = W1 ⊕ W2 .
3.7.7. Muestre que todo espacio vectorial finitamente generado es una suma directa de subespacios vectoriales
de dimensión 1.
3.7.8. Demuestre que si W es un subespacio de un espacio vectorial V entonces existe un subespacio Z de V
tal que V = W ⊕ Z
3.7.9. Demuestre que si V = W1 ⊕ · · · ⊕ Wn , entonces
1. dim V =
Pn
i=1
dim Wi .
2. Si v ∈ V entonces v se escribe de manera única como v = w1 + · · · + wn , con wi ∈ Wi para i = 1, . . . , n.
3.7.10. Sean H1 y H2 subespacios de un espacio vectorial V , si dim H1 = dim H2 = dim V − 1 entonces
dim(H1 ∩ H2 ) = dim V − 2. Deduzca que dos planos en R3 siempre siempre tienen una intersección no trivial.
3.7.11. Sean H y K subespacios de un espacio vectorial V , si dim H = dim V −1 y KH entonces dim(H ∩K) =
dim K − 1.
3.7.12. Si A, B ⊆ V son subconjuntos de un espacio vectorial V y A ∩ B = Φ muestre que L(AU B) =
L(A) ⊕ L(B), donde L(A) = intersección de los subespacios que contienen a A.
3.7.13. Sean V = W1 ⊕ · · · ⊕ Wt y Bi ⊂ Wi , para i = 1, . . . , t. Considere B = B1 ∪ · · · ∪ Bt .
117
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
1. Muestre que si Bi es LI para i = 1, . . . , t, entonces B es LI.
2. Muestre que si Bi es una base para Wi para i = 1, . . . , t, entonces B es una base de V .
3.7.14. Si W1 = {A ∈ Mn (R) | aij = 0 para i ≥ j} es el conjunto de matrices estrictamente triangulares
superiores y y W2 = {A ∈ Mn (R) | aij = 0 para i < j} es el conjunto de matrices triangulares inferiores
entonces Mn (R) = W1 ⊕ W2 .
3.7.15. Si V y W son subespacios de Rn con dim V >
n
2
y dim W >
n
2
entonces V ∩ W 6= Φ.
3.7.16. Sea T : V −→ W una transformación lineal, si V = H1 ⊕ H2 y T (H1 ) ∩ T (H2 ) = {0} entonces
T (V ) = T (H1 ) ⊕ T (H2 ).
3.7.17. Si T : V −→ W es un isomorfismo y V = H1 ⊕ H2 entonces W = T (H1 ) ⊕ T (H2 ).
3.7.18. Sea T : V −→ V una TL, demuestre que existe k > 0 tal que V = Im(T k ) ⊕ Ker(T k ).
3.7.19. Si T : V −→ W un isomorfismo y V = H1 ⊕ H2 entonces W = T (H1 ) ⊕ T (H2 ).
118
Capı́tulo 4
Ortogonalidad en Rn
En este capı́tulo se define el producto interno usual en espacios vectoriales sobre R y se muestra como se
define, a través de este producto, la norma de un vector y el ángulo entre vectores en Rn . Esto a la vez nos
permitirá hablar de ortogonalidad y proyección ortogonal de un vector sobre un subespacio. Se dará también
el método de los mı́nimos cuadrados, el cual es una aplicación de proyección ortogonal. Al final se define el
concepto de base ortogonal, la importancia de estas bases y el proceso de Gramm-Schmidt, el cual es un método
para calcular este tipo de bases. Se termina el capı́tulo con la llamada descomposición QR de una matriz, la
cual se obtiene a partir del proceso Gramm-Schmidt.
4.1.
Producto interno en Rn
Comenzamos el capı́tulo con la definición de producto interno o producto escalar de vectores en Rn .
 
 
α1
β1
 
 
 . 
 . 
Definición 4.1. Sean v =  ..  y w =  ..  vectores en Rn , definimos el producto escalar de v y w,
 
 
αn
βn
denotado por v · w, por la fórmula
v · w = α1 β1 + · · · + αn βn =
n
X
αi βi .
i=1
 
 
1
−1
 
 
 
 
Ejemplo 4.1. Sean v = 2 y w = −1, entonces v · w = 1 · (−1) + 2 · (−1) + 3 · 2 = −1 − 2 + 6 = 3.
 
 
2
3
 
 
−1
1
 
 
 
 
Ejemplo 4.2. (MatLab) Sean v = 1 y w = −1. El producto escalar v · w se calcula en MatLab como se
 
 
0
1
muestra a continuación
119
120
>> v = [1; 1; 1]; w = [−1; −1; 0]; v ′ ∗ w
y se tiene que v · w = −2.
Observación 4.1. (Propiedades del producto escalar) Sean v, w, z ∈ Rn
1. (v + w) · z = v · z + w · z
2. v · (w + z) = v · w + v · z
3. (αv) · w = v · (αw) = αv · w
4. v · v ≥ 0 y v · v = 0 si y solo si v = 0.
5. v · w = w · v.
El producto por escalar induce una geometrı́a en Rn , ya que a partir de este, podemos definir la longitud (o
norma) de un vector y la distancia entre vectores.


α1
 
 . 
Definición 4.2. (Norma de un vector) Sea v =  ..  un vector en Rn , definimos la norma de x, denotada
 
αn
por ||v||, por la fórmula
q
√
||v|| = v · v = α12 + · · · + αn2 .

−1
 
 
Ejemplo 4.3. De acuerdo a esta fórmula, la norma del vector v = −1 está dada por
 
2

||v|| =
p
(−1)2 + (−1)2 + 22 =
√
6.
Definición 4.3. (Distancia entre vectores) Sean v y w vectores en Rn , la distancia entre v y w está dada
por la fórmula ||w − v||.
 
 
1
−1
 
 
 
 
Ejemplo 4.4. Sean v = 2 y w = −1, entonces la distancia entre v y w está dada por
 
 
3
2
||w − v|| =
p
(−1 − 1)2 + (−1 − 2)2 + (2 − 3)2 =
√
14.
Observación 4.2. Si v y w son vectores en Rn , entonces se cumple que
v · w = ||v|| ||w||cosθ,
donde θ es el ángulo formado por v y w.
(4.1)
121
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
v−w
v
θ
w
b
O
La Ecuación (4.1) se obtiene de la siguiente forma: aplicando la ley de cosenos (en el plano generado por
los vectores v y w ) obtenemos
||v − w||2 = ||v||2 + ||w||2 − 2||v||||w|| cos θ,
(4.2)
pero, por la definición de norma y las propiedades del producto escalar tenemos
||v − w||2 = (v − w) · (v − w) = v · v − v · w − w · v + w · w = ||v||2 − 2v · w + ||w||2 .
(4.3)
Por tanto de las Ecuaciones (4.2) y (4.3) se tiene que
v · w = ||v|| ||w||cosθ.
Definición 4.4. (Vectores ortogonales) Sean v, w ∈ Rn .
1. Decimos que v y w son ortogonales si v · w = 0.
2. Usando la Ecuación (4.1) definimos el ángulo entre v y w, esto es,
v·w
−1
El ángulo entre v y w = cos
.
(4.4)
||v|| ||w||
 
 
1
1
 
 
 
 
Ejemplo 4.5. Sean v = −1 y w = 1, encuentre el ángulo que forman v y w y determinar si son
 
 
1
2
ortogonales.
Solución. El producto escalar v · w = 1 − 1 + 2 = 2, entonces los vectores no son ortogonales. El ángulo θ
formado por v y w está dado por la Ecuación (4.4), ası́:
√ !
v·w
2
2
−1
−1
−1
√ √
θ = cos
= cos
= cos
.
||v||||w||
3
6 3
 
 
1
1
 
 
 
 
 0
 0

 
Ejemplo 4.6. Calcular el ángulo formado por los vectores v = 
  y w =  .
 1
 0
 
 
0
1
√
√
Solución Nótese que v · w = 1 + 0 + 0 + 0 = 1, ||v|| = 2 y ||w|| = 2. Entonces de acuerdo a la Ecuación
(4.4) tenemos que
el ángulo entre v y w = cos−1
v·w
||v|| ||w||
= cos−1
1
√ √
2 2
= cos−1
1
= 60◦ .
2
122
Definición 4.5. (Espacios ortogonales) Sean V y W subespacios de Rn , decimos que V y W son ortogonales
si v · w = 0 para todo v ∈ V y w ∈ W .
    
  






1
−1 
0 



   
 






 
  






−1 1
−1
 ,   y W =   subespacios de R4 , entonces V y W son
Ejemplo 4.7. Sean V = gen 
   



−2 1

 0 






















 0
 1 

1 
 
  

1
0
a
 
  

 
  

−1
1  −a + b 
 + b  = 
 y todo elemento
ortogonales ya que todo elemento en v ∈ V tiene la forma v = a 
 
  

−2
1 −2a + b
 
  

0
1
b
   
−1
−c
   
   
−1 −c
  
w ∈ W tiene la forma w = c 
  =  , donde a, b y c son números reales, por tanto
 0   0
   
1
c
v · w = −ac + (−a + b)(−c) + (−2a + b)0 + bc = −ac + ac − bc + bc = 0.
Los subespacios ortogonales satisfacen lo siguiente.
Lema 4.1. Sean V y W subespacios ortogonales de Rn , entonces
1. V ∩ W = {0},
2. Si {v1 , . . . , vr } y {w1 , . . . , ws } son bases para V y W , respectivamente, entonces el conjunto
{v1 , . . . , vr , w1 , . . . , ws }
es linealmente independiente.
Demostración. 1. Sea v ∈ V ∩ W , entonces como V y W son ortogonales se tiene que v · v = 0 y por las
propiedades del producto interno se tiene que v = 0.
2. Supongamos que α1 v1 + · · · + αr vr + β1 w1 + · · · + βs ws = 0, entonces
α1 v1 + · · · + αr vr = −β1 w1 − · · · −s ws ∈ V ∩ W.
Por la parte 1. tenemos que α1 v1 + · · · + αr vr = 0 y por tanto α1 = · · · = αr = 0, de esto se sigue que
−β1 w1 − · · · − βs ws = 0 y como {w1 , . . . , ws } es una base entonces β1 = · · · = βr = 0.
El caso que estudiaremos a fondo en este capı́tulo es cuando los dos subespacios ortogonales son complementarios, esto lo definimos a continuación.
Definición 4.6. (Complemento ortogonal) Sea V un subespacio de Rn , definimos el complemento ortogonal de V, al cual denotaremos por V ⊥ , como el conjunto
V ⊥ = {w ∈ Rn | v · w = 0, para todo v ∈ V }.
123
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
El siguiente teorema nos da un algoritmo para calcular la base para el complemento ortogonal de un subespacio
V de Rn .
Teorema 4.2. Sea A una matriz de tamaño m × n, entonces tenemos que:
1. F il(A)⊥ = N ul(A),
2. Col(A)⊥ = N uliz(A).
Demostración. Sean F1 , . . . , Fm las filas y C1 , . . . , Cn las columnas de A.
1. Para la demostración de este ı́tem usamos el Lema 1.9.
“⊆”Sea x ∈ F il(A)⊥ , entonces v · x = 0 para todo v ∈ F il(A), en particular, 0 = Fit · x = Fi x, para i = 1, . . . , m.
De donde
es decir x ∈ N ul(A).



  
F1
F1 x
0
 

  
 .. 
 ..   .. 
Ax =  .  x =  .  =  .  ,
 

  
Fm
Fm x
0

F1 x


 . 
“⊇”Sea x ∈ N ul(A), entonces 0 = Ax =  .. , por tanto para i = 1, . . . , m tenemos que 0 = Fi x = Fit · x.


Fm x
Ahora si v ∈ F il(A), entonces v = a1 F1 + · · · + am Fm y por tanto v · x = a1 F1 · x + · · · + am Fm · x = 0 y por
| {z }
| {z }

tanto x ∈ F il(A)⊥ .
=0
=0
2. Como Col(A) = F il(At ) por el ı́tem 1. se sigue que Col(A)⊥ = F il(At )⊥ = N ul(At ) = N uliz(A).
A continuación describimos el procedimiento para calcular el complemento ortogonal, el cual se deduce del
teorema anterior.
Procedimiento 4.1. (Cálculo del complemento ortogonal). Sea {v1 , . . . , vk } una base para V , para cal-
cular una base para V ⊥ hacemos lo siguiente:
 
vt
 1
.
1. Definimos la matriz A =  ..  y de esta forma V = F il(A).
 
vkt
2. Sea W = N ul(A) entonces W = V ⊥ , esto por el Teorema 4.2, ya que V ⊥ = F il(A)⊥ = N ul(A) = W .
    



  1  0 




  








0
0
,  .
Ejemplo 4.8. Calcular V ⊥ si V = gen 







0  1 



   




 1
1 
124
 
 
0
1
 
 

 
 
 
0
0
1 0
v1t
 

 =
Solución. Sea v1 = 
  y v2 =  , debemos calcular N ul(A) donde A =
1
0
0 0
v2t
 
 
1
1
está en forma escalonada reducida entonces tenemos que
 
x
 1
 
x2 
x = −x4
  ∈ N ul(A) si y solo si 1
 
x3 
x3 = −x4
 
x4
 
 

  
−1
0
−x4
x1
 
 

  
 
 

  
 0
1
x2   x2 
 = x2   + x4   .
 
si y solo si 
 
 

 =
−1
0
x3  −x4 
 
 

  
1
0
x4
x4
0 1
1 1

, como A
   



−1 
0


   








1  0 
 ,   es una base para V ⊥ .
Por el procedimiento indicado arriba y el Teorema 2.16 se concluye que 
   

0 −1




   




 0
1 
Ejemplo 4.9. (MatLab)
Calcular
el complemento ortogonal V ⊥ del subespacio V de R5 generado por los



2
1
 
 
 
 
−1
3
 
 
 
 
vectores v1 =  1  y v2 = 2.
 
 
 
 
 0
2
 
 
1
1
 
v1t
Solución. Sea A =  , necesitamos calcular N ul(A), lo cual hacemos en MatLab como sigue
v2t
>> format rat, A = [2, −1, 1,
0,1; 1, 3,2, 2,

 
 1]; null(A)




−4/7
−2/7
−5/7



 
 














−3/7 −4/7 −1/7




 
 


 
 

⊥
Se obtiene que V = gen  1  ,  0  ,  0  .

 
 





 
 









0 
1
0
















1
0
0
Terminamos le sección con el siguiente resultado que explica porque a V ⊥ se le llama el complemento orto-
gonal de V .
Corolario 4.3. Sea V ⊆ Rn un subespacio entonces Rn = V ⊕ V ⊥ .
125
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
 
vt
 1
.
Demostración. Sea {v1 , . . . , vk } una base de V , definiendo A =  .. , por el procedimiento anterior tenemos
 
vkt
que V = F il(A) y V ⊥ = N ul(A) y por tanto
dim V + dim V ⊥ = dim F il(A) + dim N ul(A) = dim Col(A) + dim N ul(A) = n = dim Rn .
Nótese además que V y V ⊥ son, por definición, conjuntos ortogonales y por tanto V ∩ V ⊥ = {0} (Lema 4.1),
se sigue del Problema 3.7.3 que Rn = V ⊕ V ⊥ .
Problemas
4.1.1. Sean v = (2, 3, −5) y w = (3, 0, 4) determine lo siguiente:
a. ||v||
b. ||w||
c. v · w
d. el ángulo formado por v y w
e. la distancia entre v y w
4.1.2. Determine si el par de vectores dados es ortogonal, si no lo es, determine el ángulo formado por ellos.
a. v = (2, −3) y w = (3, 2)
b. v = (1, 4, −7) y yw(2, 3, 2)
c. v = (1, 1, 1) y w = (1, 1, −1).
4.1.3. Encuentre la relación entre α y β para que los vectores v = (1, 1, 2, α) y w = (−β, 2, 3, 4) sean ortogonales.
4.1.4. Calcule una base para V ⊥ en cada uno de los siguientes casos:
1.
V = gen{(1, 3, 1), (1, 1, 2)}
2.
V = gen{(2, 1, 1, 0)}
3.
V = gen{(1, 0, 0, 0, 1), (1, 2, 3, 4, 5)}
4.1.5. Calcule una base para V ⊥ si V = {(x, y, z, t) | x + 2y + 3z + 4t = 0}.


1 1 1 0
.
4.1.6. Calcule una base para V = F ilA donde A = 
0 1 1 1
4.1.7. Sean v, w, z ∈ Rn , si se sabe que v · w = 3, v · v = 4, v · z = −1, w · w = 1 y w · z = 2, determine lo
siguiente:
1. una combinación lineal de los vectores w y z que sea ortogonal a v,
2. la distancia entre los vectores v y w.
3. Explique porqué el ángulo formado por v y z es obtuso.
4. v · (−w)
5. v · (w + z)
6. (v − 2w) · (w − 3z)
7. el ángulo formado por v y w
4.1.8. Determine todos los vectores v ∈ Rn tal que ||v|| = α con α un real positivo.
4.1.9. Demuestre las propiedades de producto escalar enunciadas en la Observación 4.1
126
4.1.10. Determine el ángulo que forma el vector v = (1, 1, 1, 1) con cada uno de los vectores de la base estándar
de R4 .
4.1.11. Sea A ∈ Mn (R) una matriz siméstrica, demuestre que N ulA es el complemento ortogonal de ColA.
4.1.12. Demuestre que si V = {(x1 , . . . , xn ) | α1 x1 + · · · + αn xn = 0} entonces se tiene que
V ⊥ = gen{(α1 , . . . , αn )}.
4.1.13. Sean v, w ∈ Rn , demuestre que v + w y v − w son ortogonales si y sólo si ||v|| = ||w||.
Deduzca que un paralelogramo es un rombo si y sólo si sus diagonales son perpendiculares.
4.1.14. Sea A ∈ Mn (R), demuestre que Rm = F ilA ⊕ N ulA, deduzca que si V ⊆ Rn es un subespacio entonces
Rm = V ⊕ V ⊥ .
4.1.15. Sea A ∈ Mn (R) una matriz, demuestre que v ∈ N ulA ∩ F ilA si y sólo si v = 0.
4.1.16. Encuentre una matriz A tal que el vector v = (1, 2, 2) pertenezca a
1. al espacio fila y el espacio columna de A,
2. al espacio nulo y el espacio columna de A.
4.1.17. Sean V, W ⊆ Rn subespacios, demuestre
1. Si V ⊆ W entonces W ⊥ ⊆ V ⊥ ,
2. (V ⊥ )⊥ = V ,
3. (V + W )⊥ = V ⊥ ∩ W ⊥ ,
4. (V ∩ W )⊥ = V ⊥ + W ⊥ .
4.1.18. Encuentre contraejemplos que muestren que las siguientes afirmaciones son falsas
1. Si V y W son subespacios ortogonales de Rn entonces V ⊥ y W ⊥ son subespacios ortogonales.
2. Si V y W son subespacios ortogonales y W y Z son subespacios ortogonales entonces V y Z son subespacios
ortogonales.
3.
4.1.19. Calcule una base de V si se sabe que {(1, 2, −1, 0), (0, 2, 1, 3)} es una base de V ⊥
4.1.20. Demuestre que para todo v, w ∈ Rn se tiene que |v · w| ≤ ||v||||w||. (Esta desigualdad se conoce como la
desigualdad de Cauchy-Schwartz.)
4.1.21. Demuestre que lo siguiente
1. v · w = 0 para todo w ∈ Rn si y sólo si v = 0.
127
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
2. v = w si y sólo si v · z = w · z para todo z ∈ Rn .
4.1.22. Demuestre que para todo v, w ∈ Rn se cumple lo siguiente
1. v · w = 14 (||v + w||2 − ||v − w||2 ),
2. v · w = 12 (||v + w||2 − ||v||2 − ||w||2 ),
3. ||v + w||2 + ||v − w||2 = 2||v||2 + 2||w||2 . (Esta igualdad es conocida como la Ley del paralelogramo.)
4.1.23. Un vector u ∈ Rn se llama si ||u|| = 1. Demuestre que si w ∈ Rn el vector u =
1
||w|| w
es unitario.
Muestre además que si u y w son vectores LD con u unitario (esto es equivalente a decir que u y w están
en la lı́nea ) entonces w = ±||w||u. (El caso positivo se da cuando los vectores tienen la misma dirección).
4.2.
Proyección Ortogonal sobre un Vector
En esta sección se muestra como calcular la proyección ortogonal de un vector sobre otro, la fórmula que
se obtiene se verifica fácilmente. Usaremos la fórmula obtenida para generalizarla obteniendo la fórmula de la
proyección de un vector en un subespacio.
Definición 4.7. Sean v y w vectores en Rn , la perpendicular desde el extremo del vector v a la lı́nea que
contiene a w determina un punto sobre esta lı́nea, el vector que va desde el origen hasta este punto es llamado
la proyección ortogonal de v sobre w, denotado por proyw v.
v
θ
v
w
v
b
O
w
θ
b
O
θ
p = proyw v
b
w
p = proyw v
p = proyw v
O
Nótese que el vector proyw v es el múltiplo de w más cercano a v.
La siguiente proposición proporciona una fórmula para calcular la proyección ortogonal de un vector sobre
otro.
Proposición 4.4. Sean v y w vectores en Rn , la proyección ortogonal del vector v sobre el vector w está dada
por
proyw v =
v·w
w.
w·w
Demostración. Sea p = proyw v, θ el ángulo formado entre v y w y u un vector unitario en la dirección de w
128
b
B
v
w
θ
b
1
||w|| w
P
p = proyw v
u
O
Se sigue que p = ||p||u y u =
b
(Problema 4.1.23 ) y por tanto
p=
||p||
w.
||w||
(4.5)
Como el triángulo ∆OBP en la figura anterior es un triángulo rectángulo, tenemos que cos θ =
de la Observación 4.2 se sigue que
v·w
||w||
||p||
||v|| .
Además,
= ||v|| cos θ. Por tanto
||p|| =
v·w
.
||w||
(4.6)
De las Ecuaciones (4.5) y (4.6) se sigue que
p=
v·w
v·w
w=
w.
2
||w||
w·w
Ejemplo 4.10. Sean v = (1, 0, 1, −1) y w = (2, 2, 1, 0), se sigue que v · w = 3 y w · w = 9. Por tanto
proyw v = 39 w = 13 w = (2/3, 2/3, 2/3, 0).
4.2.1.
La matriz proyección.
La última fórmula se puede expresar matricialmente de la siguiente forma:
Nótese que wwt es una matriz y a la matriz
P =
1
wwt
wt w
wt v
1
v·w
w = t w = t wwt v.
w·w
ww
ww
(4.7)
se le llama la matriz de la proyección sobre w y tiene la propiedad que para todo v ∈ Rn , P v = proyw v.
 
 
1
1
 
 
 
 
Ejemplo 4.11. Sean v = 1 y w = 0, calcular la matriz que proyecta sobre w y usarla para calcular
 
 
2
1
proyw v.


1 0 2




Solución. Nótese que w w = w · w = 5 y ww = 0 0 0


2 0 4
matriz

1 0
1

P = 0 0
5
2 0
t
t
por tanto la matriz de la proyección sobre w es la

2


0 .

4
129
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Ahora, proyw v = P v =
1
5

1 0


0 0

2 0
 
1
2
 
 
0 1 =
 
1
4
"7#
Ejemplo 4.12. (MatLab)Sean a =
proyw v del vector v sobre w.
7
7
7
7
 
3
 
1  
0 .
5 
 
6
" −2 #
yb=
−1
1
0
1
, calcule la matriz que proyecta sobre w y la proyección
Solución. La matriz de que proyecta sobre w está dada por P =
1
wwt . Esto lo podemos calcular con MatLab
wt w
como sigue
>> format rat, w = [−2; −1; 1; 0; 1]; P = inv(w′ ∗ w) ∗ (w ∗ w′ )
ası́ la matriz de la proyección está dada por

P =

4/7 2/7 −2/7 0 −2/7
2/7 1/7 −1/7 0 −1/7
−2/7 −1/7 1/7 0 1/7 
0
0
0 0 0
−2/7 −1/7 1/7 0 1/7
Para calcular la proyección del vector v sobre w, proyw v, seguimos los comandos en MatLab
>> v = [7; 7; 7; 7; 7]; P ∗ v
Se obtiene que proyw v = −w.
La matriz de la proyección satisface las siguientes condiciones.
Teorema 4.5. Sea w ∈ Rn y P =
1
wwt la matriz proyección, entonces para todo v ∈ Rn tenemos lo
wt w
siguiente
1. P v = proyw v ∈ gen{b},
2. v − P v ⊥ w,
3. P P v = P v, en general P 2 = P ,
4. si v ∈ gen{w} entonces P v = v,
5. v ⊥ w si y solo si P v = 0.
Demostración. Se deja como ejercicio.
Problemas
4.2.1. Sean v = (2, 3, −5) y w = (3, 0, 4) calcule lo siguiente:
a. proyw v
b. proyw v
c. la matriz de la proyección sobre w y
d. la matriz de la proyección sobre v
4.2.2. Repita el problema anterior si v = (0, 1, 2, 3, 2, 1, 0) y w = (−3, −2, −1, 0, 1, 2, 3). (Use Matlab).
4.2.3. Determine el múltiplo del vector v = (2, 2, 1) más cercano al vector w = (1, 1, 1).
130
4.2.4. Si v y w son vectores en Rn tal que v · w = 4, w · w = 2 y v · v = 1, determine los vectores proyw v y
proyv w en términos de w y v respectivamente.
4.2.5. Encuentre la matriz de la proyección sobre la lı́nea x + y = 0 en R2 .
4.2.6. Demuestre el Teorema 4.5.
4.2.7. Sea v = (1, 2, 2, 3), si sabe que la proyección proyw v de v sobre un vetor w está dada por proyw v =
(2, 2, 2, 2) y ||w|| = 2, determine el vector w.
4.2.8. Demuestre que la proyección proyw v es independiente del vector escogido en gen{w}. Es decir,
proyαw v = proyw v,
para todo α ∈ R.
4.2.9. Demuestre que si Pv es la matriz que proyecta sobre un vector v ∈ Rn entonces rangoPv = 1. (Este es
un caso particular del Problema 1.2.14).
4.3.
Proyección Ortogonal sobre un Subespacio
El principal objetivo de la sección es extender el concepto de proyección sobre un vector, al de proyección
sobre un subespacio (ver figura abajo) y construir una matriz P que al multiplicarla por un vector x, el resultado
P x es el vector proyección. De hecho, esta matriz será obtenida generalizando la matriz dada por la Ecuación
(4.7) y la definiremos como sigue.
h
Sea {v1 , . . . , vk } una base para un subespacio H de Rn y sea A = v1
matriz
···
i
vk , vamos a demostrar que la
P = A(At A)−1 At
(4.8)
satisface las condiciones de la matriz proyección enunciadas en el Teorema 4.5.
v
H
p = proyH v
b
O
Proyección de v sobre H
Nótese que la Fórmula (4.7) la podemos escribir en la forma:
P =
1
vv t = v(v t v)−1 v t ,
vt v
131
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
de esta manera se ve que en realidad que (4.8) es simplemente una generalización de (4.7).
Ahora vamos a demostrar que la matriz definida en (4.8) determina la proyección sobre el subespacio H.
Para esto necesitaremos los siguientes lemas preliminares.
Lema 4.6. Sea A una matriz, entonces N ul(A) = N ul(At A).
Demostración. “⊆ ” Sea x ∈ N ul(A), entonces Ax = 0 y por tanto At Ax = At 0 = 0. Concluimos que
x ∈ N ul(At A).
“⊇ ” Sea x ∈ N ul(At A), entonces At Ax = 0, y multiplicando a la izquierda por xt tenemos que xt At Ax =
xt 0 = 0, por tanto
0 = xt 0 = xt At Ax = (Ax)t Ax = Ax · Ax = ||Ax||2 ,
de donde ||Ax|| = 0, pero por las propiedades del producto escalar, esto implica que Ax = 0 y por tanto
x ∈ N ul(A).
h
Lema 4.7. Sea A = v1
···
dientes entonces
i
vk una matriz donde {v1 , . . . , vk } son las columnas y son linealmente indepen-
1. At A es invertible.
2. La matriz (At A)−1 At es una inversa a la izquierda de A.
Demostración. 1. Como las columnas de A son linealmente independientes entonces
rango(A) = k, ası́ por el Teorema 2.16 se tiene que N ul(A) = {0}, entonces por el lema anterior N ul(At A) =
N ul(A) = {0} de donde rango(At A) = número de columnas de (At A), pero (At A) es una matriz cuadrada,
entonces
rango(At A) = número de columnas de (At A) = número de filas de (At A),
y por el Corolario 1.22, At A es invertible.
2. Como (At A)−1 At A = I entonces (At A)−1 At es una inversa a la izquierda de A.


1 0




Ejemplo 4.13. Calcular una inversa a la izquierda de la matriz A = 1 1.


1 2
Solución. Observe que los vectores columna de la matriz A son linealmente independientes. Comencemos calculando At A y su inversa.

At A = 
1 1
0 1

 1
1 

1
2 
1


0

3

1 = 

3
2



3
5
−3
1
 y por tanto (At A)−1 = 
.
6
5
−3
3
Por el Lema 4.7 resta calcular (At A)−1 At , esto es,


1
5
−3
1

L = (At A)−1 At = 
6 −3
0
3


5
1
= 
6 −3
1 2
1 1

2 −1
.
0
3
132
El lector puede verificar fácilmente que LA = I.
Ejemplo 4.14. (MatLab) Usar MatLab para calcular la inversa a la izquierda de la matriz A =
"1
2 1 2
1 −1 2 1
1 3 2 2
1 2 2 1
1 1 3 2
#
.
Solución. Usamos MatLab para calcular la inversa a la izquierda con la fórmula dada en el Teorema 4.7, como
sigue
>> format rat; A = [1, 2, 1, 2; 1, −1, 2, 1; 1, 3, 2, 2; 1, 2, 2, 1; 1, 1, 3, 2]; L = inv(A′ ∗ A) ∗ A′
la inversa a la izquierda de A está dada por
" 2/3
L=
1
−1/3
1
−1/12 −1/4
1/6
1/4
−13/24 −1/8 1/12 1/8
11/24 −1/8 1/12 −7/8
−4/3
−1/12
11/24
11/24
#
.
El siguiente resultado es el caso dual del lema anterior, más especı́ficamente, el caso en que las filas de la
matriz son LI.
Corolario 4.8. Sea A una matriz cuyas filas son linealmente independientes, entonces se tiene que
1. AAt es invertible,
2. La matriz At (AAt )−1 es una inversa a la derecha de A.
Demostración. Como las filas de A son linealmentes entonces las columnas de At son linealmente independientes, usando el Lema 4.7 tenemos que (At )t At = AAt es invertible y por tanto (AAt )−1 existe y además
como AAt (AAt )−1 = I, es decir, la matriz At (AAt )−1 es una inversa a la derecha de A.


1 1 1
, calcular una inversa a la derecha de A.
Ejemplo 4.15. Sea A = 
0 1 1
Solución: Es fácil ver que las filas de A son linealmente independientes. Primero calculamos AAt y su inversa


 1 0







1
1
1
3
2
2
−2
1


 de donde (AAt )−1 = 
.
AAt = 
 1 1 = 
2 −2


0 1 1
2 2
3
1 1
Ahora calculamos la inversa a la derecha At (AAt )−1



1 0

1
2


R = At (AAt )−1 = 1 1 

 2 −2
1 1
Nuevamente se deja al lector verificar que AR = I.



2 −2


−2

= 1
0
1 .
2

3
0
1
Ahora usamos los resultados obtenidos en esta sección para construir la matriz proyección de un vector sobre
un subespacio dado.
h
Teorema 4.9. Sean H un subespacio de Rn , {h1 , . . . , hk } una base para H y A = h1
P = A(At A)−1 At entonces para todo v ∈ Rn se tiene lo siguiente
···
i
hk . Si definimos
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
133
1. P v ∈ H,
2. v − P v ∈ H ⊥ ,
3. P 2 = P ,
4. v ∈ H si y sólo si P v = v,
5. v ∈ H ⊥ si y sólo si P v = 0.
Demostración. Primero observese que H = Col(A) y que si x ∈ Rk , entonces Ax ∈ Col(A) = H, esto ya que
 
x1
 
 .. 
si x =  .  entonces
 
xk
 
x1
h
i 
 .. 
(4.9)
Ax = h1 · · · hk  .  = x1 h1 + · · · + xk hk ∈ Col(A) = H.
 
xk
Más aún, si h ∈ H, entonces h = x1 h1 + · · · + xk hk y por la Ecuación (4.9) h = Ax.
1. P v = A (At A)−1 At v = Av ′ ∈ Col(A) = H.
|
{z
}
v′
2. Debemos demostrar que si h ∈ H entonces h · (v − P v) = 0.
Sea h ∈ H, entonces existe x tal que h = Ax y por tanto
h · (v − P v) = Ax · (v − P v) = Ax · v − Ax · P v
= (Ax)t v − (Ax)t P v
= xt At v − xt At P v
= xt At v − xt At A(At A)−1 At v
|
{z
}
I
t
t
t
t
= x A v − x A v = 0.
3. P 2 = P P = A (At A)−1 At A(At A)−1 At = A(At A)−1 At = P .
{z
}
|
I
4. Sea v ∈ H, entonces existe x tal que v = Ax y por tanto
P v = P Ax = A (At A)−1 At A x = Ax = v.
|
{z
}
I
Para la otra implicación si v = P v, por el numeral 1. tenemos P v ∈ H, por tanto v = P v ∈ H.
5. ”⇒”Supongamos que v ∈ H ⊥ , entonces v · h = 0, para todo h ∈ H, en particular v · hi = 0 para i = 1, . . . , k.
Entonces tenemos que



 
  
ht1
ht1 v
h1 · v
0
 

 
  
 .. 
 ..   ..   .. 
t
A v =  .  v =  .  =  .  = . ,
 

 
  
htk
htk v
hk · v
0
134
y por tanto
P v = A(At A)−1 |{z}
At v = A(At A)−1 0 = 0.
=0
t
”⇐”Supongamos que P v = 0, entonces A(A A)
−1
t
A v = 0, multiplicando esta ecuación a ambos lados por At
obtenemos
At 0 = At A(At A)−1 Av = IAt v = At v.
|{z}
|
{z
}
=0


=I
ht
 1
.
Como At =  ..  tenemos que 0 = hti v = hi · v, para i = 1, . . . , k. Por tanto v ∈ H ⊥ .
 
htk
Estas propiedades demuestran que P v satisface las condiciones del vector proyección de v sobre H.
h
Definición 4.8. Sean H un subespacio de Rn , {v1 , . . . , vk } una base para H, A = v1
Definimos la proyección de v sobre H, denotada por proyH v, como el vector:
···
proyH v = P v,
donde P es la matriz P = A(At A)−1 At .
    
 



1
0 
1

 
    

 
   
Ejemplo 4.16. Sean v = 1 y H = gen 1 , 1 , calcular el vector proyH v.

 
   




 0
3
1 


1 0




Solución. Sea A = 1 1, entonces proyH v = A(At A)−1 At v.


0 1

At A = 
1
0




 1 0


2
1
1 0 
2
1

 de donde (At A)−1 = 

 1 1 = 
3 −1

1 2
1 1 
0 1

Finalmente tenemos
1


A(At A)−1 = 1

0


0
1
  2
1
 3 −1
1



2 −1


−1

= 1
 1
1 .
3


2
−1
2

−1 
 1
1


proyH v = A(At A)−1 At b =  1
1 
3
 0
−1
2

2

−1
,
2
 
   
 1
0
0
 1   
1 0 





 1 = 6 = 2
,
1 1   3   
3
2
6
i
vk y v ∈ Rn .
135
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
 
0
 
 
entonces proyH v = 2 .
 
2
Ejemplo 4.17.
matriz que
sobre el subespacio
H de R6 generado por los


 2proyecta
la1 

 2Calcular
 1 (MatLab)
11
1
vectores v1 =  11 , v2 = 
1
0
−1
3 ,
1
1
1
2
1
3
0
2
1
v3 =  21  y v4 =  21 . Si b = 11e1 = 
0
0
0
0
0
 calcular proyH b.
Solución. La matriz de la proyección está dada por P = A(At A)−1 At , usamos el siguiente comando en MatLab
>> A = [1, 2, 1, 2; 1, −1, 2, 1; 1, 3, 2, 2; 1, 1, 1, 1; 1, 1, 3, 2; 0, 1, 0, 1]; P = A ∗ inv(A′ ∗ A) ∗ A′
obtenemos que la matriz de la proyección está dada por
P = proyH


=


7/11 1/11 1/11 3/11 −1/11 4/11
1/11 8/11 −3/11 2/11 3/11 −1/11
1/11 −3/11 8/11 2/11 3/11 −1/11 

3/11 2/11 2/11 6/11 −2/11 −3/11 
−1/11 3/11 3/11 −2/11 8/11 1/11
4/11 −1/11 −1/11 −3/11 1/11 7/11
 7 1 1 3
8 −3 2
1  11 −3
8 2
=
3 2 2 6
11 −1 3 3 −2
−1 4 
3 −1
3 −1 
−2 −3 .
8 1
4 −1 −1 −3 1 7
La proyección del vector b sobre H está dado por proyH b = P b, ası́ que en MatLab hacemos lo siguiente
>> b = [11; 0; 0; 0; 0; 0]; P ∗ b 
y obtenemos que proyH b = 

7
1
1
3 .
−1
4
Terminamos la sección con la siguiente observación.
Observación 4.3. Por el Corolario 4.3, si H es un subespacio de Rn entonces Rn = H ⊕ H ⊥ . Por tanto todo
vector v ∈ R se puede descomponer como una suma de un vector en H y un vector en H ⊥ . Esto se logra de la
siguiente forma.
Sea v ∈ Rn y P la matriz que proyecta sobre H, entonces por el Teorema 4.9 se tiene que P v ∈ H y v−P v ∈ H ⊥ .
Por tanto
v = |{z}
Pv +v − Pv
| {z }
∈H
∈H ⊥
es la descomposición de un vector como suma de un vector en H y un vector perpendicular a H. Nótese que,
por el Teorema 3.26, esta descomposición es única .

Ejemplo 4.18. En el ejemplo anterior, H = gen{v1 , v2 , v3 , v4 } ⊆ R6 y x = 11e1 , como proyH x = 
entonces podemos descomponer a x como la suma de vectores

x = proyH x + (x − proyH x) = 
| {z } |
{z
}
∈H
∈H ⊥
Problemas

7
1
1
3
−1
4

+
4
−1
−1 
−3 .
1
−4

7
1
1
3 ,
−1
4
136

1


4.3.1. Sea A =  1

−2
b sobre H.
 
1
 

 

−1, b = 0 y H = ColA. Calcule la matriz que proyecta sobre H y la proyección de
 

1
4
1

4.3.2. Sea V = gen{(1, 2, 0, 0), (1, 0, 1, 0)}, calcule la matriz que proyecta sobre V y el vector en V más cercano
al vector v = (2, 1, 0, −1).
4.3.3. Sea V = gen{(1, 1, 0, 1), (0, 0, 1, 0)}, calcule la matriz que proyecta sobre V ⊥ y la proyección del vector
v = (2, 1, 0, −1) sobre V ⊥ .
"1 1 1 1#
4.3.4. Sean A =
1
1
1
0
1
2
0
1
1
3
0
1
2
4
0
0
yB=
1 1 1 1 1
1 1 0 2 1
1 1 0 3 2
1 1 0 4 3
. Use MatLab para calcular lo siguiente
1. una inversa a la izquierda de la matriz A,
2. una inversa a la derecha de la matriz B,
3. las matrices que proyectan sobre ColA y ColB,
4. la proyección del vector v = (1, 2, 3, 2, 1) sobre ColA,
5. la proyección del vector w = (1, 2, 2, 1) sobre ColB.

0


4.3.5. Sea A una matriz 4×3, se sabe que At A =  1

−1
1 −1



0 , determine N ulA y F ilA.

0
0
0
4.3.6. Sea W ⊆ Rn un subespacio y sean P1 , P2 las matrices que proyectan sobre W y sobre W ⊥ , respectivamente. Demuestre que P1 + P2 = I y que P1 P2 = 0.
4.3.7. Si P = P t P muestre que P es una matriz proyección, es decir, P 2 = P .
4.3.8. Sea H ⊆ Rn y P la matriz que proyecta sobre H, demuestre lo siguiente
1. ColP = H y rangoP = dim H.
2. N ulP = H ⊥ . (Recuerde que P es simétrica.)
Use lo anterior para calcular bases para H y H ⊥ si P =
1
3

2
1


 1 2

−1 1

−1


1 .

2
4.3.9. Sea H ⊆ Rn un subespacio y sea P la matriz que proyecta sobre H, demuestre que
H = {v ∈ Rn | P v = v}.
En general, muestre que si P ∈ Rn es una matriz proyección, es decir, P 2 = P entonces ColP = {v ∈ Rn |
P v = v}.
137
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
4.3.10. Sea H un subespacio vectorial de Rn y P es la matriz que proyecta sobre H. Viendo a P como aplicación
lineal
P :
Rn
−→
Rn
, demuestre que P/H = IdH donde P/H : H −→ H es la restricción de P a H.
v
7→ P v
Demuestre también que P/H ⊥ ≡ 0.
4.3.11. Sea H ⊆ Rn un subespacio y w ∈ Rn , definimos el conjunto w + H como
w + H = {w + h | h ∈ H}.
Sean v ∈ Rn y w ∈ H, demuestre que proyH v = w si y sólo si v ∈ w + H ⊥ .
4.4.
Mı́nimos Cuadrados
El método de los mı́nimos cuadrados consiste en encontrar una solución “óptima” a un sistema que no tiene
solución. La idea es la siguiente.
Dado un sistema de ecuaciones Ax = b, sabemos que el sistema tiene solución si y solo si b ∈ Col(A), esto
ya que
h
b = Ax = C1
···


x1
i 
 . 
Cn  ..  = x1 C1 + · · · + xn Cn ∈ gen{C1 , . . . , Cn } = Col(A),
 
xn
donde C1 , . . . , Cn son las columnas de A.
De esto se deduce que si el sistema Ax = b es inconsistente, entonces b ∈
/ Col(A) y el vector más cercano a
b que pertence a Col(A) es el vector proyCol(A) b = A(At A)−1 At b. Como el sistema Ax = b es inconsistente, lo
reemplazamos por el sistema consistente Ax̂ = proyCol(A) b = A(At A)−1 At b. Este último sistema tiene solución
dada por x̂ = (At A)−1 At b. A esta solución la llamamos la solución de los mı́nimos cuadrados.
Definición 4.9. Sea A una matriz cuyas columnas son linealmente independientes y b ∈ Rn , si el sistema
Ax = b es inconsistente entonces la solución de los mı́nimos cuadrados al sistema está dada por
−1 t
A b.
x̂ = At A
Esta solución al sistema Ax = b “es la mejor” en el sentido que éste se reemplaza por el sistema Ax = b̄ donde
b̄ = proyColA b es el vector más cercano a b para el cual el sistema Ax = b̄ si tiene solución.
 


1
2 1
 


 


Ejemplo 4.19. Considere el sistema Ax = b donde A = −1 1 y b = 2. Se verifica fácilmente que el
 


0
1 1
sistema es inconsistente (usar el Teorema 1.2). Como las columnas de A son LI, se puede usar el método de
los mı́nimos cuadrados para calcular la “mejor solución”. Esta está dada por x̂ = (At A)
a continuación.
−1
At b, y la calculamos
138

At A = 
da por
2
1





2 1

6 2
−1 1 


 de donde (At A)−1 =
 −1 1 = 

2 3
1 1 
1 1


−1 t
1  3 −2 2
x̂ = At A
Ab=
14 −2
1
6
1
14


3
−2

−2
 entonces la mejor solución está da6
 
 1
 

−1 1 
−6
1


 .
2 =
1 1   14 18
0
Otra aplicación de los mı́nimos cuadrados es la de ajustar datos encontrados en observaciones, que se esperan
se ajusten a una linea pero sin embargo los puntos obtenidos experimentalmente no son colineales. Supongamos
que los valores observados son (x1 , y1 ), (x2 , y2 ), . . . , (xn , yn ) y supongamos que los datos deben satisfacer la
ecuación y = mx + b, esto es,
y1 = mx1 + b
y2 = mx2 + b
..
.
yn = mxn + b

 
x1 1  
y1

  
..  m
.  .
, como los puntos (x1 , y1 ), . . . , (xn , yn )
Esto lo podemos escribir matricialmente en la forma  ..  =  ..

.
 b
  
xn 1
yn
no todos satisfacen la ecuación y = mx + b, el sistema es inconsistente. Usando la solución de los mı́nimos cua
drados obtenemos que la mejor solución al sistema esta dado por

x1

 ..
donde A =  .

xn

 
y1
1

 
.. 
 .. 
y y =  . .
.

 
1
yn
−1 t
x̂ = At A
A y,
Ejemplo 4.20. Supongamos que los valores observados son (−2, 0), (1, 0) y (2, 3), es fácil ver que estos valores
no pertecen son colineales. Los valores m y b de la linea y = mx 
+ b que mejor
  se ajusta a los datos están dados
 
−2 1
0


 
m




−1
en el vector x̂ =   donde x̂ = (At A) At y con A =  1 1 y y = 0.




b
2 1
3






 −2 1



9
1
3
−1
−2
1
2


, entonces se tiene que (At A)−1 = 1 
, y por
  1 1 = 
Nótese que At A = 
26

1 3
−1
9
1 1 1 
2 1
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
tanto
x̂ = (At A)−1 At y =
De aquı́ tenemos que m =
y=
15
26 x
+
15
26
y b=


1  3 −1 −2
26 −1
1
9
21
26
139
 
 0
   

15
1 2 
15
1


  =  26  .
 0 =
21
1 1   26 21
26
3
y por tanto la ecuación de la linea que mejor se ajusta a los datos es
21
26 .
Los mı́nimos cuadrados también se pueden usar para calcular ecuaciones polinómicas de cualquier grado (en
general cualquier función) que mejor se ajusten a ciertos datos, generalizando el ejemplo anterior que se hizo
para lineas. Esto lo ilustramos a contiuación.
Ejemplo 4.21. (MatLab) Un experimeto arrojó los puntos (−1, 2), (1, 0), (3, 1) y (2, −1), si se espera que
estos puntos estén sobre una parábola y = ax2 + bx + c, calcule la ecuación de la parábola que mejor se ajuste
a los datos.
Solución. Como se espera que los puntos satisfagan la ecuación y = ax2 + bx + c, evaluando esta en los puntos
obtenemos
2=a−b+c
0=a+b+c
1 = 9a + 3b + c
−1 = 4a + 2b + c


 
1 −1 1  
2

 a
 

   
1
1 1    0 
  b  =  , el cual es inconsistente (ver Teorema
Estas ecuaciones son equivalentes al sistema 


 
9
3 1    1 

 c
 
4
2 1
−1
1.2), por tanto, usando MatLab para calcular la solución de losmı́nimos cuadrados

 para
 obtener los coeficientes
1 −1 1
2


 


 
1
 0
1 1
 y v =  , obtenemos
a, b y c, los cuales estan dados por x̂ = (At A)−1 At v con A = 


 
9
 1
3 1


 
4
2 1
−1
′
′
>> A = [1,−1, 1; 1, 1, 1; 9,
 3, 1; 4, 2, 1]; v = [2; 0; 1; −1]; x̂ = inv(A ∗ A) ∗ A ∗ v
21/44




ası́ x̂ =  −283/220  . De este resultado obtenemos que la ecuación que mejor se ajusta a los datos es


7/22
y=
7
21 2 283
x −
x+
44
220
22
⇔
220y = 105x2 − 283x + 70.
El siguiente ejemplo muestra como este método se puede usar en problemas del dı́a a dı́a.
140
Ejemplo 4.22. La demanda d de un artı́culo en venta depende del precio p del mismo. En un concesionario
de motocicletas se observo lo siguiente:
Si el precio por unidad es $3 millones se venden 5 motos en un dı́a. Si el precio se incrementa a $3.5 millones
se venden 4 motos en dı́a y cuando el precio se incrementa a $4 millones, se venden solo 2 motos en el dı́a.
Asumiendo que la relación entre precio y demanda es lineal, d = pm + b, determine la ecuación que mejor
se ajusta a estos datos. Determine cuantas motos se venderı́an en un dı́a si se fija el precio en $2.7 millones.
Solución. De acuerdo a los datos tenemos el sistema
5 = 3m + b
4 = 3,5m + b
2 = 4m + b
donde el precio está dado en millones.
 

 
5
1
 


m
 




y v = 4. Se verifica
Escrito matricialmente tenemos la ecuación Ax = v con A = 3,5 1, x =
 


b
2
4 1
que el sistema es inconsitente. La solución de los mı́nimos cuadrados está dada por


−3
.
x̂ = (At A)−1 At v = 
14,16

3
Se sigue que la ecuación que mejor se ajusta a los datos es d = −3p + 14,16.
Si se fija el precio en $2.7 millones, se obtiene una demanda diaria d = −3 ∗ 2,7 + 14,16 = 6,06, es decir, se
espera vender unas 6 motos por ese precio.
La interpretación de la pendiente es el crecimiento de la demanda por cada incremento de un millón en el
precio (ya que d′ (p) = m esta es la razón de cambio de la demanda con relación al precio). En este caso, como
m = −3, quiere decir que por cada incremento de un millón en el precio, la demanda disminuye en 3.
El siguiente ejemplo muestra que, incluso en algunos casos, se puede hasta encontrar curvas no polinómicas
que se ajusten a un sistema de datos.
Ejemplo 4.23. Encuentre la curva exponencial y = aecx que mejor se ajuste a los puntos (1, 1), (2, 8) y (3, 8).
Solución. La curva la podemos “linearizar” aplicando logaritmo a ambos lados
ln y = ln(becx ) = ln b + cx |{z}
ln e = ln b + cx.
=1
Por tanto reemplazando los datos en esta ecuación obtenemos el sistema
 

1
0
0 = ln 1 = ln b + c
 

 

ln 8 = ln b + 2c equivalente al sistema ln 8 = 1
 

1
ln 8
ln 8 = ln b + 3c

1  
 ln b

2   .
 c
3
141
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Este sistema
de
los mı́nimos cuadrados está dada por x̂ = (At A)−1 At v donde
 

 es inconsistente yla solución


 
0
0
1 1
 




4/3
1/3
−2/3
ln
b
 




, por tanto
A = 1 2, x̂ =   y v = ln 8 = ln 2 3. Nótese que (At A)−1 At = 
 




−1/2
0
1/2
c
3
ln 8
1 3

x̂ = ln 2 
4/3
−1/2
1/3
0
 
 

 0

 

−
ln
2
−1
−2/3 
ln(1/2)

=

.
=
3 = ln 2 
3 ln 2


3/2
1/2
1,04
2
3
Se sigue que ln b = ln(1/2), lo que implica que b = 1/2, y c ≈ 1,04. Concluimos que la ecuación de la “mejor”
curva está dada por
y=
1 1,04x
e
.
2
Problemas
Ejemplo 4.24. Use mı́nimos cuadrados para calcular la “mejor” solución al sistema
 


1
1 0
 


3x = 10
 


b. Ax = v si A = 0 1 y v = 1 .
a.
 


4x = 5
0
1 1
4.4.1. Determine la ecuación que mejor se ajusta a los puntos (1, 1), (2, 4), (3, 8) y (4, 8) si la relación es
1. lineal (y = mx + b),
2. cuadrática (y = ax2 + bx + c),
3. exponencial (y = aebx ).
4.4.2. Si en el Ejemplo 4.22 se sabe además que por el precio de $4.5 millones no se logró ninguna venta,
determine
1. la ecuación lineal d = mp + b que mejor se ajusta a los datos.
2. la ecuación cuadrática d = ap2 + bp + c que mejor se ajusta a los datos y en este caso determine la máxima
demanda posible.
4.4.3. En una plaza de mercado se ha observado que la demanda de naranja se comporta de acuerdo a la
siguiente tabla
precio
500
1000
1500
2000
3000
demanda
600
450
400
300
100
donde el precio está dado en pesos y la demanda en toneladas. Use MatLab para determinar la ecuación que
mejor se ajusta a los datos si la relación entre las variables es
142
1. lineal ( d = mp + b).
2. Cuadrática (d = ap2 + bp + c).
3. Cúbica (d = ap3 + bp2 + cp + d).
4. Exponencial (d = aebp ).
4.4.4. La población P de un pequeño poblado se está reduciendo de forma exponencial P = aebt , la tabla de
población es como sigue:
año
2004
2009
2011
2014
habitantes
5mil
4.5mil
4mil
3.8mil
Usar mı́nimos cuadrados para responder lo siguiente:
1. Una ecuación que modele la cantidad de habitantes con respecto al tiempo.
2. La cantidad de habitantes en el año 2020.
3. El año en el cual se espera que la población se reducirı́a a 2500 habitantes.
4.5.
El Proceso Gramm-Schmidt
El objetivo de esta sección es introducir los conceptos de base ortogonal y base ortonormal y mostrar que
es posible construir, a partir de cualquier base para un subespacio de Rn , una base ortonormal para éste. Este
proceso es conocido como el proceso Gramm-Schmidt. Tambiénn veremos las ventajas que se obtienen de tener
una base ortogonal u ortonormal, las cuales permite calcular proyecciones de manera sencilla. Comenzamos con
las definiciones de conjunto ortogonal, conjunto ortonormal, base ortogonal y base ortonormal.
Definición 4.10. Sean v1 , . . . , vk vectores en Rn ,
1. decimos que {v1 , . . . , vk } es un conjunto ortogonal si los vectores v1 , . . . , vk son ortogonales entre sı́, es decir,
si vi · vj = 0 para 1 ≤ i 6= j ≤ k,
2. decimos que {v1 , . . . , vk } es una conjunto ortonormal, si es un conjunto ortogonal y ||vi || = 1 para i =
1, . . . , k,
3. si {v1 , . . . , vk } es una base de Rn y si es un conjunto ortogonal (ortonormal), decimos que {v1 , . . . , vk } es una
base ortogonal (ortonormal) de Rn .
 
 
0
1
 
 
 
 
 
 
Ejemplo 4.25. El conjunto {v1 , v2 , v3 } donde v1 = −1 , v2 = 1 y v3 = 0 es un conjunto ortogonal de
 
 
 
1
0
0
 
 
 
0
1
1
 
 
 






R3 y los vectores w1 = √12 −1 , w2 = √12 1 y w3 = 0 forman una conjunto ortonormal de R3 .
 
 
 
1
0
0

1

143
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Observación 4.4. Si {v1 , . . . , vk } es un conjunto ortogonal, a partir de éste podemos formar un conjunto
ortonormal. Basta con definir wi =
1
||vi || vi ,
para i = 1, . . . , k, de lo cual se sigue que el conjunto {w1 , . . . , wk }
es un conjunto ortonormal. Al vector wi se le llama la normaliazción del vector vi , esto hace referencia al
hecho que wi es un vector normal o unitario (de norma 1) en la misma lı́nea que contiene a vi y con la misma
dirección.
Esto ya que para i 6= j se tiene que wi · wj =
Además wi · wi =
1
||vi || vi
· ||v1j || vj =
1
||vi ||2
1
||vi || vi
· ||v1j || vj =
vi · vi = 1.
| {z }
1
||vi || ||vj ||
vi · vj .
| {z }
=0
=||vi ||2
De hecho, el conjunto ortonormal {w1 , w2 , w3 } del ejemplo anterior se construyó a partir del conjunto ortogonal {v1 , v2 , v3 } normalizando cada uno de estos vectores.
En realidad se puede verificar que los conjuntos {v1 , v2 , v3 } y w1 , w2 , w3 } son bases para R3 . Esto no es
casualidad, en general se demuestra que un conjunto orrtogonal es LI.
Lema 4.10. Sea {v1 , . . . , vk } ⊆ Rn un conjunto ortogonal con vi 6= 0 i = 1, . . . , k. Entonces el conjunto
{v1 , . . . , vk } es LI.
Demostración. Supongamos que el conjunto {v1 , . . . , vk } es ortogonal y supongamos que
α1 v1 + · · · + αk vk = 0.
(4.10)
Multiplicando a ambos lados de la Ecuación (4.10) por vi tenemos:
0 = vi · 0 = vi · (α1 v1 + · · · + αk vk )
= α1 v i · v 1 + · · · + αi v i · v i + · · · + αk v i · v k = αi v i · v i
| {z }
| {z }
| {z }
=0
6=0
=0
Se sigue que αi vi · vi 6= 0 y como vi · vi 6= 0 se debe dar que αi = 0 y esto para i = 1, . . . , n. Por tanto los
vectores v1 , . . . , vk son LI.
De este lema se sigue que si {v1 , . . . , vk } es un conjunto ortogonal (ortonormal), éste forma una base del
espacio H = gen{v1 , . . . , vk }.
A continuación definimos la noción de matriz ortogonal, este será útil en lo que sigue de la sección.
h
i
Definición 4.11. Decimos que una matriz A = v1 · · · vk es una matriz ortogonal, si vi · vj = δij para
i, j ∈ {1, . . . , ≤ k. Es decir, las columnas de A forman un conjunto ortonormal.


√1
√1
0
2
 2

 −1

√1
Ejemplo 4.26. La matriz A =  √
 es una matriz ortogonal ya que el conjunto de columnas de esta
0
2
 2

0
0 1
      

√1
√1


0 

  2   2   

 −1   1   
matriz,  √  ,  √  , 0 , es un conjunto ortonormal, lo cual se demostró en el Ejemplo4.25.

 2   2   





1 
0
0
144
La propiedad más importante de las matrices ortogonales es la siguiente.
Lema 4.11. (Propiedad de las matrices ortogonales) Sea A ∈ Mmn (R), entonces A es una matriz orto-
gonal si y sólo si At A = I.
Por tanto si A es una matriz cuadrada entonces A es invertible y A−1 = At . Si A no es cuadrada entonces At
es una inversa a la izquierdaA.
h
Demostración. Si A = v1
···
i
vk es una matriz ortogonal, entonces
 
vt
 1 h
.
At A =  ..  v1
 
vkt
···
vk

i


 t
 v2 v1
=
 ..
 .

vkt v1
v1 · v1 v1 · v2 · · ·
| {z } | {z }
 =1
=0

 v2 · v1 v2 · v2 · · ·
| {z } | {z }

=  =0
=1
 .
..
..
 ..
.
.


v · v v · v · · ·
| k{z }1 | k{z }2
=0
v1t v1
=0
v1t v2
v2t v2
..
.
···
···
..
.
v1t vk


v2t vk 

.. 
. 

vkt vk
vkt v2 · · ·

v1 · vk
| {z } 
=0 
 1 0 · · ·

v2 · vk 
0 1 ···
| {z }
 

=
=0 
. . ..

.. 
 .. ..
.


. 

0 0 ···
vk · vk 
| {z }
=1

(4.11)

0


0

..  = I.
.

1
Si At A = I se sigue de la Ecuación 4.11 que las columnas de A forman un conjunto ortonormal y por
definición A es ortogonal.
Si A es una matriz cuadrada, por el Corolario 1.22, A es invertible y A−1 = At . La otra afirmación es
inmediata.
Ejemplo 4.27.
1. Este teorema nos permitecalcular la inversa
de una matriz ortonormal de manera fácil, por el

1
1
√
√
0
2

 2

 −1
√1
Ejemplo 4.26 tenemos que la matriz A =  √
0 es una matriz ortogonal, por tanto
2

 2
0
0 1
A−1 = At =

√1
 2
 1
√
 2
0
−1
√
2
√1
2
0

0


0 .

1
2. El teorema también se puede usar para calcular
a la izquierda de matrices ortonormales cuando no

 la inversa
√1
 2
 −1
son cuadradas. Por ejemplo la matriz B =  √
 2
0


−1
√1
√
0
2
.
izquierda de B es B t =  2
1
1
√
√
0
2
2
√1
2

√1 
2
0
es una matriz ortonormal, por tanto una inversa a la
145
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Las bases ortogonales (ortonormales) tiene ventajas importantes, estas se reflejan cuando se quiere calcular
la proyección de un vector sobre un subespacio. El siguiente teorema provee una fórmula para determinar la
proyección sin usar la matriz de la proyección. La fórmula se obtiene a partir de una base ortogonal u ortonormal.
Teorema 4.12. Sea {v1 . . . , vk } una base ortonormal para un subespacio vectorial H de Rn y sea b ∈ Rn ,
entonces
proyH b = (v1 · b)v1 + · · · + (vk · b)vk .
Si la base {v1 . . . , vk } es ortogonal entonces proyH b =
h
Demostración. Sea A = v1
···
v1 ·b
v1 ·v1 v1
+ ··· +
vk ·b
vk ·vk vk .
i
vk , entonces proyH b = A(At A)−1 At b. Como A es una matriz ortogonal
por el Teorema 4.11 se tiene que At A = I, por tanto
h
proyH b = A (At A)−1 At b = AAt b = v1
| {z }
···
=I
h
= v1
···
 
vt
i  1
.
vk  ..  b
 
vkt

v1t b
i 
 . 
t
t
vk  ..  = (v1 b)v1 + · · · + (vk b)vk
 
vkt b

= (v1 · b)v1 + · · · + (vk · b)vk .
Si la base {v1 , · · · , vk } es ortogonal, entonces por la Observación 4.4, tenemos que el conjunto {w1 , . . . , wk }
es una base ortonormal de H donde wi =
(wi · b)wi = ||v1i || vi · b ||v1i || vi = ||vvii·b||2 vi =
1
||vi || vi , con i = 1, . . . , k.
vi ·b
vi ·vi vi , por tanto
proyH b = (w1 · b)w1 + · · · + (wk · b)wk =
Entonces para i = 1, . . . , k tenemos que
vk · b
v1 · b
v1 + · · · +
vk .
v1 · v1
vk · vk

 
 
 



1
1
−1 

 
 

 

 
 
 
Ejemplo 4.28. Sea b = 1 y H = gen v1 = 1 , v2  1  . Es fácil ver que {v1 , v2 } es una base ortogonal

 
 
 





3
0
2 
de H, entonces por el teorema anterior tenemos que
 
0
 
v2 · b
2
6
v1 · b
 
v1 +
v 2 = v 1 + v 2 = v 1 + v 2 =  2 .
proyH b =
v1 · v1
v2 · v2
2
6
 
2
De hecho el este subespacio es el mismo del Ejemplo 4.16 y obtenemos, como debe ser, la misma respuesta.
Simplemente en este caso tenemos una base ortogonal de H, lo cual nos permite usar el teorema anterior sin
tener que calcular la matriz de la proyección y la cantidad de cálculos se reduce.
146
 
0
 
 
Para ver que los subespacios de este ejemplo y el ejemplo en mención coinciden, nótese que si w = 1
 
1
entonces

 
  
1/2
−1/2
0

 
  
v1 · w
v2 · w
1
3

 
  
proyH w =
v1 +
v2 = v1 + v2 = v1 + v2 = 1/2 +  1/2  = 1 = w.
v1 · v1
v2 · v2
2
6

 
  
0
1
1
Se tiene que w = proyH w y por tanto w ∈ H. Es decir, tanto {v1 , v2 } como {v1 , w} son bases de H.
El siguiente corolario también muestra la importancia de tener una base ortonormal, porque provee una
fórmula para escribir un vector en un subespacio como combinación lineal de una base ortonormal sin tener que
hacer reducción Gauss-Jordan.
Corolario 4.13. Sea H ⊆ Rn un subespacio con base ortonormal {v1 . . . , vk }. Entonces para todo b ∈ H se
tiene que
b = (b · v1 )v1 + · · · + (b · vk )vk .
Más aún, si {v1 . . . , vk } una base ortogonal de H, entonces b =
b·v1
v1 ·v1 v1
+ ··· +
b·vk
vk ·vk vk .
Demostración. Si b ∈ H por el Teorema 4.9 tenemos que proyH b = b, por tanto el resultado se sigue aplicando
el teorema anterior.


 
 
1
0
 
 
 
 
 
 
Ejemplo 4.29. De acuerdo al Ejemplo 4.25 Los vectores v1 = −1 , v2 = 1 y v3 = 0 forman una base
 
 
 
0
0
1
 
1
 
 
3
ortogonal para R . Usando el teorema anterior podemos escribir el vector b = 1 de la siguiente forma:
 
1
b=
1
b · v2
b · v3
0
2
1
b · v1
v1 +
v2 +
v3 = v1 + v2 + v3 = v2 + v3 .
v1 · v1
v2 · v2
v3 · v3
2
2
1
 
 
 
0
 
 
 
 
 
 
Ejemplo 4.30. De acuerdo al Ejemplo 4.25 Los vectores w1 =  √
−1  , w2 =  √
1  y w3 = 0 forman una
 2
 
 2
1
0
0
 
1
 
 
3
base ortonormal para R . Usando el teorema anterior podemos escribir el vector b = 1 de la siguiente forma:
 
1
1
√
2
1
√
2
√
2
b = (b · w1 )w1 + (b · w2 )w2 + (b · w3 )w3 = 0w1 + √ w2 + w3 = 2w2 + w3 .
2
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
147




 
 
 
 
Ejemplo 4.31. El conjunto v1 =  √1  , v2 =  √1  es una base ortonormal para el plano xy (o z = 0)

 2 
 2






0
0
 
1
 
 
entonces usando el teorema anterior para calcular proyH b con H = plano xy y b = 2 obtenemos:
 
1






1
√
2


−1
√
2
 
1
 
3
1
 
proyH b = (b · v1 )v1 + (b · v2 )v2 = √ v1 + √ v2 = 2 .
 
2
2
0
El Teorema 4.12 y el Corolario 4.13 muestran la importancia de tener una base ortogonal u ortonormal
para un subespacio, sin embargo hasta ahora no sabemos como se puede calcular tal base. El siguiente teorema
muestra como, a partir de una base arbitraria de un subespacio de Rn , podemos construir una base ortogonal.
Teorema 4.14. (El proceso Gramm-Schmidt) Sea H ⊆ Rn un subespacio y sea {v1 , . . . , vk } una base de
H si hacemos
w1 = v 1 ,
W1 = gen{w1 }
w2 = v2 − proyW1 v2
W2 = gen{w1 , w2 }
w3 = v3 − proyW2 v3
..
.
W3 = gen{w1 , w2 , w3 }
..
.
wk−1 = vk−1 − proyWk−2 vk−1
Wn−1 = gen{w1 , . . . , wn−1 }
wk = vn − proyWk−1 vk
Entonces {w1 , . . . , wk } es una base ortogonal de H.
Más aún, si hacemos qi =
1
||wi || wi
para i = 1, . . . , n, entonces {q1 , . . . , qn } es una base ortonormal de H.
Demostración. Por definición de proyección ortogonal tenemos que wi = vi − proyWi−1 vi es ortogonal al
subespacio Wi−1 para i = 1, . . . , k y por tanto wi ortogonal a cada uno de los vectores w1 , . . . , wi−1 . Se sigue
que los vectores w1 , . . . , wk son ortogonales entre sı́, es decir, el conjunto {w1 , . . . , wk } es un conjunto ortogonal.
En consecuencia, por el Lema 4.10, el conjunto {w1 , . . . , wi } es una base ortogonal de Wi , , para i = 1, . . . , k−1, y
{w1 , . . . , wk } es una base ortogonal del subespacio que ellos generan, gen{w1 , . . . , wk }. Solo nos resta demostrar
que H = gen{w1 , . . . , wk }.
Como el conjunto {w1 , . . . , wk } es base de gen{w1 , . . . , wk }, se sigue que dim H = k = dim gen{w1 , . . . , wk }.
Por tanto es suficiente demostrar que w1 , . . . , wk ∈ H, ya que de esta forma se sigue que gen{w1 , . . . , wk } ⊆ H
y por tener dimesiones iguales se concluye que los subespacios son iguales (Problema ???).
Primero nótese que w1 = v1 ∈ H.
También tenemos que w2 = v2 − proyw1 v2 = v2 −
v2 ·w1
w1 ·w1 w1
∈ H.
148
Continuando por inducción supongamos que w1 , . . . , wi−1 ∈ H. Como el conjunto {w1 , . . . , wi−1 } es una base
ortogonal de Wi−1 , entonces por el Teorema 4.12 tenemos que
proyWi−1 vi =
vi · wi−1
v i · w1
w1 − · · · −
wi−1
w1 · w1
wi−1 · wi−1
(4.12)
por tanto
wi = vi − proyWi−1 vi = vi −
v i · w1
vi · wi−1
w1 − · · · −
wi−1 ∈ H.
w1 · w1
wi−1 · wi−1
Concluimos que w1 , . . . , wk ∈ H y por tanto el conjunto {w1 , . . . , wk } es una base ortogonal para H.
De la Observación 4.4 se sigue que el conjunto {q1 , . . . , qk } es una base ortonormal.
Observación 4.5. Si {v1 , . . . , vk } es una base para un subespacio H de Rn , entonces por la Ecuación (4.12),
los vectores w1 , . . . , wk de la base ortogonal del proceso Gramm-Schmidt están dados por
w1 = v 1 ,
v2 ·w1
w1 ·w1 w1
v2 ·w1
w1 ·w1 w1
w2 = v 2 −
w3 = v 3 −
..
.
wk−1 = vk−1 −
wk = v k −
Ejemplo 4.32. Sean v1 =
1
1
0
0
, v2 =
1
1
0
v2 ·w2
w2 ·w2 w2
vk−1 ·w1
w1 ·w1 w1
vk ·w1
w1 ·w1 w1
0
−
y v3 =
− ··· −
− ··· −
1
0
0
1
(4.13)
vk−1 ·wk−1
wk−1 ·wk−1 wk−1
vk ·wk
wk ·wk wk
y H = gen{v1 , v2 , v3 }. Calcule lo siguiente
1. una base ortonormal {q1 , q2 , q3 } para H.
1
2. Escriba el vector v = 31 en términos de la base ortonormal.
−1
3. Calcule la proyección del vector z =
1
1
1
1
sobre H.
Solución.
1. Usaremos las ecuaciones dadas en (4.13) para calcular los vectores w1 , w2 y w3 y después los normalizamos.
#
"
En primer lugar se tiene que w1 = v1 , el vector w2 está dado por w2 = v2 −
finalmente w3 = v3 −
w1 ·v3
w1 ·w1 w1
−
w2 ·v3
w2 ·w2 w2
= v3 − 21 w1 −
(−1/2)
3/2 w2
w1 ·v2
w1 ·w1 w1
= v3 − 21 w1 + 13 w2 =
= v2 − 21 v1 =
" 1/3 #
−1/3
1/3
1
−1/2
1/2
1
0
y
.
Se verifica fácilmente que los vectores w1 , w2 y w3 son ortogonales. Para la base ortonormal, con el fin de agilizar
cálculos, se puede trabajar con múltiplos de los vectores
que no hayan denominadores.
1 , w2 y w3 de tal
forma
−1 w
1
−1
1
y u3 = 3w3 =
Para este efecto tomamamos u1 = w1 , u2 = 2w2 =
1 .
2
Finalmente se tiene que los vectores
1
1 1
q1 =
u1 = √ 10 ,
||u1 ||
2 0
forman una base ortonormal para H.
3
0
q2 =
1
1
u2 = √
||u2 ||
6
−1 1
2
0
y
q3 =
1
1
u3 = √
||u2 ||
12
1
−1
1
3
149
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
2. Por el Corolario 4.13 tenemos que
4
4
4
v = (q1 · v)q1 + (q2 · v)q2 + (q3 · v)q3 = √ q1 + √ q2 − √ q3 .
2
6
12
La última igualdad se obtiene racionalizando el denominador.
En términos de la base ortogormal
v=
u1 · v
u2 · v
u3 · v
2
1
u1 +
u2 +
u3 = 2u1 + u2 − u3 .
u1 · u1
u2 · u2
u3 · u3
3
3
3. Por el Teorema 4.12 tenemos que
√
√
√
6
12
2
4
2
q2 +
q3 .
proyH z = (q1 · z)q1 + (q2 · z)q2 + (q3 · z)q3 = √ q1 + √ q2 + √ q3 = 2q1 +
3
3
2
6
12
La última igualdad se obtiene racionalizando el denominador.
En términos de la base ortogormal
v=
u1 · v
u2 · v
u3 · v
1
1
u1 +
u2 +
u3 = u1 + u2 + u3 .
u1 · u1
u2 · u2
u3 · u3
3
3
Finalizamos la sección mostrando la idea geométrica detras del proceso de Gramm-Schmidt.
En la siguiente figura se muestran los vectores w1 y w2 (en rojo) obtenidos al aplicar Gram-Schmidt a un
par de vectores v1 y v2 . En ésta se ve que los vectores w1 y w2 son ortogonales y pertencen al mismo plano que
v1 y v2 .
w2 = v2 − proyv1 v2
v2
b
proyv1 v2
O
v 1 = w1
En la siguiente figura se muestra el caso en dimensión 3. Si se tienen vectores LI v1 , v2 y v3 y ya se han
determinado los vectores ortogonales w1 y w2 , en la figura se muestra como se obtiene el vector w3 , ortogonal
al plano W2 = gen{w1 , w2 }. Obteniendo ası́, los vectores w1 , w2 y w3 (en rojo), los cuales forman una base
ortogonal.
v3
w3 = v3 − proyW2 v3
w2
proyW2 v3
v2
b
O
v1 = w1
W2
150
Problemas
4.5.1. Verifique que las matrices son ortogonales y que su correspondiente transpuesta es una inversa a la
izquierda

1/2
A =  1/2
1/2
1/2
√ 
−1/ 6
√
−1/ 6 
√
2/ 6
0
 √
√
√ 
1/ 3 1/ 6
1/ 2
 √
√
√ 


B = 1/ 3 1/ 6 −1/ 2 .
 √

√
0
1/ 3 −2/ 6
4.5.2. Sean w1 = (1, 1, 2), w2 = (2, 0, −1) y w3 = (1, −5, 2), H = gen{w1 , w2 } y v = (1, 1, 1), haga lo siguiente
1. verifique que X = {w1 , w2 , w3 } es una bas ortogonal,
2. escriba el vector v en términos de la base X,
3. calcule la proyección, proyH v, del vector v sobre H,
4. calcule el vector u y proyH u si se sabe que u · w1 = 5, u · w2 = 3 y u · w3 = −1,
5. calcule el vector z ∈ H tal que z · w1 = 3, z · w2 = 5,
6. muestre que H ⊥ = gen{w3 }.
4.5.3. Sea {w1 , . . . , wn } una base ortogonal de Rn y H = gen{w1 , . . . , wk }, muestre que H ⊥ = gen{wk+1 , . . . , wn }.
Demuestre también que si v = α1 w1 + · · · + αn wn entonces proyH v = α1 w1 + · · · + αk wk .
4.5.4. Aplique el procedo de Gramm-Scdmidt para calcular una base ortonormal del subespacio generado por los
vectores v1 , v2 y v3 si
 
 
 
 
 
 
0
1
1
1
0
0
 
 
 
 
 
 
 
 
 
 
 
 
a. v1 = 1 , v2 = 1 , v3 = 1 . b. v1 = 1 , v2 = 0 , v3 = 1 .
 
 
 
 
 
 
1
1
0
1
1
0
 
 
 
1
0
0
 
 
 
 
 
 
−1
 1
 0

 
 
c. v1 = 
  , v2 =   , v3 =   .
 0
−1
 1
 
 
 
0
0
−1
4.5.5. Calcule una base ortogonal y una base ortonormal para cada uno de los espacios en los problemas 4.3.1,
4.3.2, 4.3.3 y 4.3.4. En cada caso calcule la proyección del vector indicado en cada problema sobre el respectivo
subespacio en términos de la base ortogonal y en términos de la base ortonormal.
4.5.6. Encuentre los valores de α y β tal al aplicar el proceso de Gramm-Schmidt a los vectores v1 , v2 y v3 se
obtengan los vectores w1 , w2 y w3 , donde
 
 
 
β
1
1
 
 
 
 
 
 
v3 =  1  ,
v2 =  1  ,
v1 = 1 ,
 
 
 
0
α
0
 
1
 
 
w1 = 1 ,
 
0
 
0
 
 
w2 =  0
 
1
y

−1
 
 
w3 =  1  .
 
0

151
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
4.5.7. Determine los vectores v1 , v2 y v3 tal que al aplicar el proceso Gramm-Schmidt se obtienen los vectores
w1 = (1, 1, 1, 1), w2 = (1, 1, −1, −1) y w3 = (1, −1, 1, −1) si se sabe además que v2 · w1 = −2, v3 · w1 = 8 y
v3 · w2 = 2.
4.5.8. Determine todos los posibles vectores v1 y v2 talque al aplicar el proceso Gramm-Schmidt y normalizar
el resultado sean los vectores q1 = (1/2, 1/2, 1/2, 1/2) y q2 = (1/2, 1/2, −1/2, −1/2).
4.5.9. Determine las columnas faltantes de tal forma que cada una de las siguientes matrices sean ortogonales.




1/2
1/2
√




1/2
1/ 6
√
√






1/ 3
1/ 6
1/2
1/2
√








1/2
1/
6
√
√






b.
B
=
q
c.
C
=
a. A =  1/ 3
q
q
q
q
q


1/ 6 3
1/2 −1/2 3 4 5 
3
4 
√





 1/2 −2/ 6

√
√




 1/2 −1/2

1/ 3 −2/ 6


1/2
0
0
0
Ayuda: En cada caso los vectores qi , i = 3, 4, 5, pertenecen al complemento ortogonal del espacio generado por
las dos primeras columnas de la matriz.
4.5.10. Sea A = [v1 · · · vn ] ∈ Mn (R), donde v1 , . . . , vn son las columnas de A, y sea B =
t
Demuestre que si {v1 , . . . , vn } es un conjunto ortogonal entoncesB es la inversa
 de A.
1
1
1




Use lo anterior para determinar la inversa de la matriz A = 1
1 −1 .


1 −2
0
h
1
v1 ·v1 v1
···
1
vn ·vn vn
4.5.11. Si A es de tamño m × n con columnas ortonormales, demuestre que P = AAt es una matriz proyección,
es decir, P 2 = P .
4.5.12. Sea u ∈ Rn un vector unitario y v ∈ Rn arbitrario. Demuestre lo siguiente:
1. la matriz Q = I − ut u es una matriz simétrica ortogonal.
2. Si U = gen{u} demuestre que Qv es la proyección de v sobre U ⊥ .
3. Calcule Q si u = (1/2, 1/2, 1/2, 1/2) y la proyección de v = (1, 2, 3, 4) sobre U y U ⊥ .
4.5.13. Una isometrı́a de Rn es un isomorfismo T : Rn −→ Rn tal que T (v)·T (w) = v ·w, para todo v, w ∈ Rn .
Muestre que T es una isometrı́a si y sólo si la matriz
E TE
de T es una matriz ortogonal.
4.5.14. Sea T : Rn −→ Rn una isometrı́a, demuestre lo siguiente:
1. ||T (v)|| = ||v||, para todo v ∈ R, es decir, T preserva longitudes.
2. T preserva ángulos, es decir, ∡(v, w) = ∡(T (v), T (w)), para todo v, w ∈ R.
3. La inversa de una isometrı́a es una isometrı́a y la composición de isometrı́as es una isometrı́a.
4. T envı́a bases ortonormales en bases ortonormales, es decir, {v1 , . . . , vn } es una base ortonormal de Rn si y
sólo si {T (v1 ), . . . , T (vn )} es una base ortonormal de Rn .
i
.
152
4.5.15. Sean A, B ∈ Mn (R) matrices ortogonales, muestre que AB y A−1 son ortogonales. (Esto muestra que
el conjunto de matrices ortogonales es un subgrupo del grupo de matrices invertibles, éste subgrupo es conocido
como el grupo ortogonal, denotado
por On (R).)

 




  cos θ
 cos θ −senθ sin θ  0 ≤ θ ≤ 2π .
 0 ≤ θ ≤ 2π ∪ 
Demuestre que O2 (R) = 

  sin θ − cos θ  sin θ
cos θ
Estas dos componentes de On (R) consisten de rotaciones en dirección antihoraria del plano y rotaciones en
dirección de las manecillas del reloj del plano. El grupo On (R) también se puede ver como el conjunto formado
por composiciones de rotaciones antihorarias y reflecciones con respecto a una lı́nea por el origen. Los geometras
se refieren a este grupo como el grupo de movimientos rı́gidos del plano que preservan el origen.
4.5.16. Sean P y Q de tamaños m × n y n × q matrices ortogonales, muestre que P Q es ortogonal.
Si m < n, es P t ortogonal?
4.6.
La Factorización QR de una Matriz
h
Teorema 4.15. Sea A = v1
···
i
vk una matriz cuyas columnas son LI, entonces exite una matriz ortogonal
Q y una matriz triangular superior R tal que A = QR.
Demostración. Sean H = gen{v1 , · · · , vk } y q1 , . . . , qk los vectores obtenidos al aplicar el proceso GrammSchmidt, es decir, los vectores obtenidos al normalizar los vectores en la Observación 4.5, los cuales forman una
base ortonormal para H. Por el Teorema 4.13 tenemos que
vi = (q1 · vi )q1 + · · · + (qk · vi )qk .
(4.14)
Recordemos que en la demostración del Teorema 4.14 vimos que gen{v1 , . . . , vi−1 } = gen{w1 , . . . , wi−1 } =
gen{q1 , . . . , qi−1 }, para i = 2, . . . , k, y como qi es ortogonal a gen{q1 , . . . , qi−1 }, por ser ortonormal a q1 , . . . , qi−1
entonces qi · v1 = 0, . . . , qi · vi−1 = 0. Como esto es para todo i = 1, . . . , k obtenemos que qi · vj = 0 para i > j.
Reemplazando esto en la Ecuación (4.14) obtenemos
vi = (q1 · vi )q1 + · · · + (qi · vi )qi ,
para i = 1, . . . , k, por tanto tenemos la ecuaciones:
v1
= (q1 · v1 )q1
v2
= (q1 · v2 )q1 + (q2 · v2 )q2
..
.
vk−1 = (q1 · vk−1 )q1 + · · · + (qk−1 · vk−1 )qk−1
vk
= (q1 · vk )q1 + · · · + (qk · vk )qk .
La cual podemos escribir matricialmente de la siguiente forma
153
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

h
v1
···
i h
v k = q1

h
Si hacemos Q = q1
···




i

qk y R = 




···



i

qk 




q1 · v 1
q1 · v 2
q1 · v 3
···
0
q2 · v 2
q2 · v 3
···
0
..
.
0
..
.
q3 · v 3
..
.
···
..
.
0
0
0
···
q1 · v 1
q1 · v 2
q1 · v 3
···
0
q2 · v 2
q2 · v 3
···
0
..
.
0
..
.
q3 · v 3
..
.
···
..
.
0
0
0
···
q1 · v k

q1 · v k



q2 · v k 


q3 · v k 

.. 
. 

qk · v k


q2 · v k 


q3 · vk  obtenemos A = QR.

.. 
. 

qk · v k
De este Teorema se desprende el siguiente procedimiento para calcular la factorización QR de una matriz.
h
Procedimiento 4.2. (Procedimiento para calcular las matrices Q y R) Sea A = v1
···
i
vk una
matriz cuyas columnas v1 , . . . , vk son linealmente independientes. Calculamos su factorización QR con los siguientes pasos:
1. Aplicamos el proceso Gramm-Schmidt y la Observación 4.5 a los vectores v1 , . . . , vk para obtener los vectores
ortogonales w1 , . . . , wk .
h
2. Se normalizan los vectores w1 , . . . , wk para obtener vectores ortonormales q1 , . . . , qk y hacemos Q = q1
3. Para 1 ≤ i ≤ j ≤ k calculamos los productos qi · vj y hacemos






R=




q1 · v 1
q1 · v 2
q1 · v 3
···
0
q2 · v 2
q2 · v 3
···
0
..
.
q2 · v 2
..
.
q3 · v 3
..
.
···
..
.
0
0
0
···
q1 · v k



q2 · v k 


q2 · v k  .

.. 
. 

qk · v k
4. De acuerdo al Teorema 4.15 tenemos que A = QR.


1 0 1




 1 1 0
, calcular las matrices Q y R tal que A = QR.
Ejemplo 4.33. Sea A = 


 0 1 0


0 0 1
 
 
 
1
0
1
 
 
 
 
 
 
1
1
0

 
 
Solución. Sean v1 = 
 , v2 =   y v3 =  , usando el Procedimiento 4.2 obtenemos lo siguiente.
0
1
0
 
 
 
0
0
1
···
i
qk .
154

1
√
2


− √16

 

 
 √1
 √1 
6


2
1. En el Ejemplo 4.32 usamos el proceso Gramm-Schdmit y obtuvimos q1 =  , q2 = 

 √2
0
 6
 
0
0


1
√
 2

 √1
2
por tanto Q = 

0

0
− √16
1
√
6
2
√
6
0
√1
12


√1
12







− √1 

 y q3 =  12 ,



 √1 

 12 

√3
12


.



− √112 
√1
12
√3
12
2. Para 1 ≤ i ≤ j ≤ 3 calculamos los productos qi · vj ,
q1 · v 1 =
√2
2
q1 · v 2 =
q2 · v 2 =



Por tanto R = 

2
√
2
1
√
2
1
√
2
0
3
√
6
−1
√
6
0
0
√4
12
√1
2
√3
6
√1
2
−1
q2 · v 3 = √
6
q3 · v3 = √412 .
q1 · v 3 =



.


1
√
2


 √1
2
3. De esta manera obtenemos que A = 

0

0
− √16
1
√
6
2
√
6
0


 √2
 2
− √112  
 0


√1
12 
√1
12
1
√
2
1
√
2
3
√
6
−1
√
6
0
√4
12
0
√1
12



.

Usamos MatLab para corroborar que A = QR:
>> Q = [1/sqrt(2), −1/sqrt(6), sqrt(3)/6; 1/sqrt(2), 1/sqrt(6), −sqrt(3)/6; 0, 2/sqrt(6), sqrt(3)/6; 0, 0, sqrt(3)/2],
R = [2/sqrt(2), 1/sqrt(2), 1/sqrt(2); 0, 3/sqrt(6), −1/sqrt(6); 00, 2/sqrt(3)], Q ∗ R
Lo que nos confirma que efectivamente A = QR.
En la Sección 5.6 del próximo capı́tulo veremos una interpretación geométrica de esta descomposición.
Problemas
4.6.1. Calcule la descomposición QR de las matrices

0 0


A = 1 1

0 1

1


1 ,

1

1 1


B = 1 0

0 1

0


1 ,

1

1 0






 1 1

C=


 2 1


0 2
y
1


−1
D=

 0

0
0
0



0
.

−1
1

0 −1
1
155
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
 √
√ 
√
1/ 3 −1/ 6
 √
3
√ 


4.6.2. Determine la matriz A si Q = 1/ 3 −1/ 6 y R = 
 √
0
√ 
1/ 3
2/ 6
√ 
4/ 3
√ .
2/ 6
4.6.3. Determine la factorización QR de una matriz A = [v1 v2 v3 ] si sabe que al aplicar el proceso GrammSchmidt a los vectores v1 , v2 y v3 se obtienen los vectores w1 = (1, 1, 1, 1), w2 = (1, 1, −1, −1) y w3 =
(1, −1, 1, −1) y se sabe además que v2 · w1 = −2, v3 · w1 = 8 y v3 · w2 = 2.


1/2
1/2




1/2
1/2 
. Determine también las posibles R. (Este
4.6.4. Determine todas las matrices A tal que Q = 


1/2 −1/2


1/2 −1/2
problema está relacionado con el Problema 4.5.8)
156
Capı́tulo 5
Determinantes
La noción de determinante es muy importante en matemáticas, a partir de este se puede definir volumen
de n-pı́pedos, los cual exhibimos en la última sección de este capı́tulo. En textos de álgebra multilineal se demuestra que el determinante, visto como función de (Rn )n en Rn , es la única n-forma n-lineal alternada tal
que det(e1 , . . . , en ) = 1, lo que permite usarla como forma volumen bien definida en Rn . En este capı́tulo, al
no usar las herramientas del álgebra multilineal, usamos los cofactores para definir el determinante. A partir de
esta definición y usando matrices elementales demostramos las propiedades de linealidad del determinante en
cada fila y cada columna, al igual que su propiedad de alternabilidad. En la Sección 5.3 demostramos la regla
del producto y el determinante de la matriz inversa. Después se introduce la matriz adjunta y una fórmula para
la inversa de una matriz a partir de ésta. También se demuestra la regla de Cramer y terminamos el capı́tulo
dando la interpretación geométrica del determinante usándolo para calcular volúmenes.
5.1.
Definición y ejemplos
En esta sección introducimos la definición de determinante y las propiedades básicas.
Definición 5.1. Sea A una matriz de tamaño m × n, para cada par (i, j) con 1 ≤ i ≤ m y 1 ≤ j ≤ n, definimos
el ij-ésimo menor de A, al cual denotaremos por Aij , como la matriz obtenida de A al eliminar su i-ésima
fila y su j-ésima columna.

1
1


Ejemplo 5.1. Sea A = 1 −1

0
2

1 1
menor es la matriz A12 = 
0 3
0 2



1 1

1 0 el 24-ésimo menor de A es la matriz A24 = 

0 2
3 0

0
.
0
157

0
 y el 12-ésimo
3
158


a11 · · · a1n


.. 
 .
..
Definición 5.2. (Determinante) Sea A =  ..
una matriz de tamaño n × n. Definimos el
.
. 


an1 · · · ann
determinante de A, el cual denotaremos por det(A), recursivamente como sigue:
Si n = 2 entonces det(A) = a11 a22 − a12 a21 .
Para n ≥ 3,
det(A) =
n
X
(−1)1+i a1i det (A1i )
i=1
= a11 det (A11 ) − a12 det (A12 ) + · · · + (−1)1+n a1n det (A1n ) .

2 −1


Ejemplo 5.2. Sea A = 0

1
1
1

0


0 de acuerdo a esta definición el determinante de A está dado por:

1
det(A) =
3
X
(−1)1+i a1i det (A1i )
i=1
= a11 det (A11 ) − a12 det (A12 ) + a13 det (A13 )






0 1
0 0
1 0

 + 0 det 
 − (−1) det 
= 2 det 
1 1
1 1
1 1
= 2(1 · 1 − 0 · 1) + (0 · 1 − 0 · 1) + 0(0 · 1 − 1 · 1)
=2
Definición 5.3. Sea A una matriz n × n, para cada par (i, j) con 1 ≤ i ≤ m y 1 ≤ j ≤ n, el ij-ésimo cofactor
de A, denotado por Cij , se define como
Cij = (−1)i+j det Aij ,
donde Aij es el ij-ésimo menor de A.
Observación 5.1. Con esta definición podemos reescribir la fórmula de del determinante como sigue:
det(A) =
n
X
i=1
A esta fórmula se le conoce como

−1 1


Ejemplo 5.3. Sea A =  0 1

−1 2
Solución: C11
a1i C1i = a11 C11 + a12 C12 · · · + a1n C1n .
la expansión por cofactores de A a lo largo de la primera fila.

0


1, calcular C11 , C12 y C13 y calcular el determinante de A.

1


1
1
 = 1 · 1 − 1 · 2 = −1,
= (−1)1+1 det A11 = (−1)2 det 
2 1
159
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

C12 = (−1)1+2 det A12 = (−1)3 det 

0
−1 1
C13 = (−1)1+3 det A13 = (−1)4 det 
det(A) = a11 C11 + a12 C12 + a13 C13
1
0
1

 = −1 (0 · 1 − 1 · (−1)) = −1,

 = 0 · 2 − 1 · (−1) = 1 y ası́
−1 2
= −1 · (−1) + 1 · (−1) + 0 · 1 = 0.
De la definición se desprenden los siguientes resultados.


a11
0 ···
0




0 
 a21 a22 · · ·


Lema 5.1. Sea A =  .
..
..  una matriz triangular inferior, entonces
..
 ..
.
.
. 


an1 an2 · · · ann
det(A) = a11 a22 · · · ann .
Es decir, el determinante de una matriz triangular inferior es el producto de las entradas en la diagonal. En
particular, el determinante de una matriz diagonal es el producto de las entradas en la diagonal.
Demostración. Por inducción sobre n.
Si n = 2 tenemos que det(A) = a11 a22 − 0a21 = a11 a22 .
Supongamos que el determinante de toda matriz triangular inferior de tamaño (n − 1) × (n − 1) es el producto
de las entradas en la diagonal. Usando la Observación 5.1 tenemos que
det(A) = a11 C11 + a12 C12 + · · · + a1n C1n = a11 C11 .
|{z}
|{z}
(5.1)
=0
=0
Pero por hipótesis de inducción tenemos que
C11

a22

 .
= (−1)1+1 det(A11 ) = 1 · det  ..

an2
···
..
.
0
..
.
···
ann



 = a22 · · · ann

(5.2)
De las ecuaciones (5.1) y (5.2) tenemos que
det(A) = a11 a22 · · · ann .
Corolario 5.2. Sea I = In la matriz identidad de tamaño n × n, entonces det(I) = 1.
En la Observación 5.1 se dijo que el determinante se obtiene por expansión por coeficientes a lo largo de la
primera fila. Esto porque en la fórmula se usan los coeficientes en esa fila. El siguiente teorema muestra que
para calcular el determinante de una matriz podemos usar coeficientes en cualquier fila o cualquier columna con
sus correspondientes menores.
160

a11

 ..
Teorema 5.3. Sea A =  .

an1
por cofactores en cualquier fila

a1n

.. 
entonces el determinante de A se puede calcular usando la expansión
. 

· · · ann
o cualquier columna, es decir, para 1 ≤ i, j ≤ n tenemos que:
···
..
.
det(A) = ai1 Ci1 + ai2 Ci2 + · · · + ain Cin =
{z
}
|
Expansión por cofactores en la fila i
n
X
aik Cik
o
(5.3)
k=1
n
X
det(A) = a1j C1j + a2j C2j + · · · + anj Cnj =
ahj Chj .
|
{z
}
h=1
(5.4)
Expansión por cofactores en la columna j
Demostración. Primero demostraremos la Fórmula (5.3) por inducción sobre n.
Para n = 2 tenemos que:
Expansión por cofactores en la segunda fila = −a21 a12 + a22 a11 = det(A).
Ahora supongamos que el teorema se cumple para cualquier matriz de tamaño (n − 1) × (n − 1) y mostremos
que det(A) = Expansión por cofactores en la fila i.
Por definición tenemos que
det(A) =
n
X
(−1)1+j a1j det(A1j ).
(5.5)
j=1
Ahora, como la matriz A1j es de tamaño (n − 1) × (n − 1), entonces por la hipótesis de inducción tenemos que
su determinante se puede calcular por expansión por cofactores en la fila i, por tanto
det(A1j ) = (−1)i+1 ai1 det((A1j )i1 ) + · · · + (−1)i+n ain det((A1j )in )
=
n
X
(5.6)
(−1)i+k aik det((A1j )ik ).
k=1
De las Ecuaciones (5.5) y (5.6) tenemos que
det(A) =
n
X
(−1)1+j a1j
j=1
=
n
n X
X
n
X
(−1)i+k aik det((A1j )ik )
k=1
(−1)1+j+i+k a1j aik det((A1j )ik ).
(5.7)
j=1 k=1
Se demostrará que la expansión por cofactores en la fila i coincide con esta fórmula.
Nótese que como Cik = (−1)i+k det(Aik ), entonces tenemos que:
Expansión por cofactores en la fila i =
n
X
k=1
aik Cik =
n
X
(−1)i+k aik det(Aik ).
(5.8)
k=1
Ahora, por definición de determinante tenemos que
det(Aik ) =
n
X
j=1
(−1)1+j a1j det((Aik )1j ).
(5.9)
161
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
De las Ecuaciones (5.8) y (5.9) tenemos
Expansión por cofactores en la fila i =
=
n
X
(−1)i+k aik
k=1
n X
n
X
n
X
(−1)1+j a1j det((Aik )1j )
j=1
(−1)i+k+1+j aik a1j det((Aik )1j ).
(5.10)
k=1 j=1
Finalmente nótese que (A1j )ik = (Aik )1j ya que ambas se obtienen al eliminar las filas 1 e i y las columnas j y
k de A. Entonces las Ecuaciones (5.7) y (5.10) son iguales, por tanto
det(A) = Expansión por cofactores en la fila i.
Similarmente se demuestra que el determinante se puede calcular por expansión en cualquier columna.


−1 0 −1




Ejemplo 5.4. Calcular el determinante de A =  2 0
1  usando expansión por cofactores en la tercera


0 1
0
fila y segunda columna.
Solución: Usando expansión por cofactores en la tercera fila tenemos:
det(A) = (−1)3+1 a31 det(A31 ) + (−1)3+2 a32 det(A32 ) + (−1)3+3 a33 det(A33 )






−1 0
−1 −1
0 −1

 + 0 det 
 − 1 det 
= 0 det 
2 0
2
1
0
1
= −1(−1 + 2) = −1.
Ahora, usando expansión por cofactores en la segunda columna tenemos:
det(A) = (−1)1+2 a12 det(A12 ) + (−1)2+2 a22 det(A22 ) + (−1)3+2 a32 det(A32 )






−1 −1
−1 −1
2 1

 − 1 det 
 + 0 det 
= −0 det 
2
1
0
0
0 0
= −1(−1 + 2) = −1.
A continuación presentamos dos propiedades importantes del determinante cuyas demostraciones son inmediatas del teorema anterior.
Corolario 5.4. Sea A una matriz de tamaño n × n, si A tiene una fila o una columna de ceros, entonces
det(A) = 0.
Demostración. Supongamos que la i-ésima fila de A es nula, esto es, para 1 ≤ j ≤ n se tiene que aij = 0,
entonces:
det(A) = Expansión por cofactores en la fila i =
n
X
j=1
aij Cij = 0.
|{z}
=0
En el caso en que haya una columna de ceros se hace una demostración similar usando expansión por la columna
de ceros.
162
Corolario 5.5. Sea A una matriz de tamaño n × n entonces det(At ) = det(A).
Demostración. Sea B = At , entonces bij = aji y Bij = Atij = Aji , donde Aij y Bij son los ij-ésimos menores
de A y de B respectivamente, entonces:
det(At ) = det(B) = Expansión por cofactores en la columna 1 =
n
X
bk1 (−1)k+1 det(Bk1 )
k=1
=
n
X
a1k (−1)k+1 det(A1k ) = det(A).
k=1




Corolario 5.6. Sea A = 



a11
a12
···
0
..
.
a22
..
.
···
..
.
0
0
···
a1n



a21 

..  una matriz triangular superior, entonces
. 

a11
det(A) = a11 a22 · · · ann .
Demostración. Se sigue del Lema 5.1 y del Corolario 5.5.
Terminamos la sección con la siguiente propiedad del determinante que será útil en el Capı́tulo 6.

Teorema 5.7. Sea A ∈ Mn (F) una matriz tal que A = 
B
C
0
D

 con B ∈ Mp (F) y D ∈ Mn−p (F) entonces
det A = det B det D.
Demostración. Por inducción sobre p.



a11 a12 · · · a1n


a22



 0 a22 · · · a2n 
..


Si p = 1, tenemos que A = 
.
..
..  entonces B = a11 , D = 
 ..
..

 .
.
.
. 


an2
0 an2 · · · ann
a11 . Aplicando cofactores a A a lo largo de la primera columna obtenemos que
···
..
.
···

a2n

.. 
= A11 y det B =
. 

ann
det A = a11 C11 + a21 C21 + · · · + an1 Cn1 = a11 det A11 = det B det D.
|{z}
|{z}
|{z}
=0
=0
=D
Supongamos ahora que el resultado es cierto para submatrices de tamaño (p − 1) × (p − 1) y que B =


a11 · · · a1p


.. 
 ..
..
. Aplicando nuevamente cofactores en la primera columna de A obtenemos que
 .
.
. 


ap1 · · · app
163
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
det A = a11 C11 + · · · + ap1 Cp1 + ap+1,1 Cp+1,1 + · · · + an1 Cn1 = a11 det A11 + · · · + (−1)p+1 ap1 det Ap1
|{z}
| {z }
=0
=0

a22

 ..
 .
= a11 det 

ap2


···
..
.
a2p
..
.
···
app
0
a22

 .
= a11 det  ..
|{z}

inducción
ap2
|
···
..
.
···
{z
B11


a12
..
.
···
..
.




C1 

 + · · · + (−1)1+p ap1 det 


ap−1,2 · · ·



0
D


a2p
a12


.. 
 .
det D + · · · + (−1)1+p ap1 det  ..
. 


app
ap−1,2
}
|

a1p
..
.
ap−1,p
···
..
.
a1p
..
.
···
{z
ap−1,p


 det D

}
=Bp1
= (a11 det B11 + · · · + (−1)p+1 ap1 det Bp1 ) det D
|
{z
}


Cp 




D

fórmula por cofactores para det B
= det B det D
Problemas
5.1.1. Calcule el determinante de las siguientes matrices




−1 1 0 2
−1
1 2 0








 3 2 0 1
 0 −1 0 0




B=
A=


 4 3 0 2
 1
2 1 0




5 3 0 1
3 −1 1 1
5.1.2.

−1
3


 1 −1
C=

 0
0

0
0
2 1



0 2


1 2

1 1

y

1 2


D = 0 2

3 2

1


2

1

a b 0 ··· 0 0
b a b ··· 0 0
 0 b a ··· 0 0 
5.1.3. Si Tn = det(An ) donde An es de la matriz tridiagonal: An = 
 ... ... ... . . . ...
entonces Tn = aTn−1 −
.. 
.
0 0 0 ··· a b
0 0 0 ··· b a
2
b Tn−2
Si a = 2 y b = −1 demuestre que Tn = n + 1. En general demuestre que si a = 2b entonces Tn = (n + 1)bn
Si a = 1 y b = 1 muestre que Tn = Tn−1 − Tn−2 . Muestre que Tn+6 = Tn para todo entero positivo n.
Determine T900 .

a b
−b
a
0 −b

5.1.4. Si Sn = det(An ) donde An es la matriz tridiagonal An = 
 ...
b2 Sn−2
0
0
..
.
0
0
0 ···
b ···
a ···
.. . .
. .

0 0
0 0
0 0
..
.
entonces Sn = aSn−1 +
.. 
.
0 ···
a b
0 ··· −b a
164
Si a = 1 y b = 1 demuestre que {Sn } es la sucesión de Fibonacci.


B C
, det A = −6 y det B = −3, determine det D.
5.1.5. Si A = 
0 D

5.1.6. Si A = 
B
0
C
D

 ∈ Mn (F) con B ∈ Mp (F) y D ∈ Mn−p (F) entonces det A = det B det D.
5.1.7. Sean A, B ∈ Mn (R) matrices triangulares superiores, demuestre que det(AB) = det A det B.
Muestre que esto también se cumple si A y B son ambas triangulares inferiores o ambas diagonales. (Ayuda:
Use el Problema 1.2.12.)
5.1.8. Sea A, B y C ∈ Mn (R), con A triangular superior, B diagonal y C triangular inferior, demuestre lo
siguiente:
b. det(BC) = det B det C .
a. det(AB) = det A det B
5.1.9. Demuestre
 la fórmula del determinante de matrices 2 × 2 y 3 × 3.

a b
, muestre que det(A) = ad − bc.
Si A = 
c d


a11 a12 a13




Si A = a21 a22 a23 , muestre que


a31 a32 a33
det(A) = a11 a22 a33 + a21 a32 a13 + a31 a12 a23 − a31 a22 a13 − a11 a32 a23 − a21 a12 a23 .
5.2.
Determinantes y operaciones elementales de fila
En esta sección mostraremos que si E es una matriz elmental y A es una matriz arbitraria, ambas de tamaño
n × n, entonces det(EA) = det E det A. Esto lo haremos considerando tres casos, uno por cada tipo de matriz
elemental. Este resultado será útil para demostrar que el determinante del producto de matrices es el producto
de los determinantes, resultado que veremos en la próxima sección.


a11 · · · a1n
 .
.. 
..
 .

.
 .
. 




Teorema 5.8. Sea A =  ai1 · · · ain  y B =


 .
.. 
..
 ..
.
. 


an1 · · · ann
multiplicar una fila i por una constante c, entonces

a11
 .
 .
 .


c · ai1

 .
 ..

an1
···
..
.
···
..
.
···
det(B) = c · det(A).

a1n
.. 

. 


c · ain  la matriz que se obtiene de A al

.. 
. 

ann
165
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Demostración. Primero nótese que para k = 1, . . . , n se tiene que Bik = Aik , ya que al eliminar la fila i de B
se obtiene la misma matriz que al eliminar la fila i de A. Por tanto,
det(B) = Expansión por cofactores en la fila i de B =
n
X
bik (−1)i+k det( Bik )
|{z}
|{z}
k=1 =c·a
=
n
X
k=1
=c·
c · aik (−1)i+k det(Aik )
n
X
k=1
=Aik
ik
aik (−1)i+k det(Aik ) = c · det(A).
Ejemplo 5.5. El teorema anterior nos dice que si todas las entradas de una fila son múltiplos de un real c,
entonces éste se puede factorizar de la fila como se muestra a continuación





1
1
2
−2
1 2 −2










det 4 2 −6 = det 2 · 2 2 · 1 2 · (−3) = 2 det 2





0
0
3
2
0 3
2
Del resultado anterior se deduce lo siguiente.
2 −2



1 −3 .

3
2
Corolario 5.9. Sea A una matriz n × n y sea E la matriz elemental que se obtiene de In al multiplicar una
fila por una constante c 6= 0 entonces det(E) = c y det(EA) = det(E) det(A).
Demostración. Por el Lema 5.1 tenemos que det In = 1 y por el teorema anterior se sigue det E = c det In = c.
Ahora, la matriz EA se obtiene de A al multiplicar la fila i por c, Teorema 1.13, se sigue por el teorema
anterior que
det(EA) = c det A = det E det A.
Ahora pasamos a mostrar el efecto que tiene un intercambio



a11 · · · a1n
a


 11
 ..


.
.
.
..
.. 
 .
 ..






 ai1 · · · ain 
 aj1



 .

 .
.
.


.
.
.
.
Teorema 5.10. Sea A =  .
.
.  y sea B = 
 .



a

a
 j1 · · · ajn 
 i1



.. 
 ..
 ..
..
 .
 .
.
. 



an1 · · · ann
an1
intercambiar las filas i y j de A, entonces
de filas en el determinante de una matriz.

· · · a1n

.. 
..
.
. 


· · · ajn 

.. 
..
.
. 
 la matriz que se obtiene de A al

· · · ain 


.. 
..
.
. 

· · · ann
det(B) = − det(A).
166
Demostración. Primero supongamos que las filas intercambiadas son consecutivas, es decir,

a11
 .
 .
 .


 ai1
A=

a(i+1)1

 .
 ..

an1
···
..
.
···
···
..
.
···


a1n
a11
 .
.. 

 .
 .
. 




a
ain 
 y B =  (i+1)1


 ai1
a(i+1)n 


 .
.. 

 ..
. 

ann
an1
···
..
.
···
···
..
.
···

a1n
.. 

. 


a(i+1)n 
.

ain 

.. 
. 

ann
Ahora, nótese que b(i+1)k = aik y B(i+1)k = Aik ya que la matriz que se obtiene al eliminar la fila i + 1 de B
coincide con la matriz que se obtiene al eliminar la fila i de A. Por tanto si usamos expansión por cofactores en
la fila i + 1 de B obtenemos:
det(B) =
=
n
X
aik (−1)i+1+k det(Aik )
b(i+1)k (−1)i+1+k det(B(i+1)k ) =
{z
}
{z
}
|
|
k=1
k=1
n
X
n
X
k=1
aik
Aik
aik (−1)(−1)i+k det(Aik ) = −
n
X
k=1
aik (−1)i+k det(Aik ) = − det(A).
En el caso general, para intercambiar las filas i y j de A se necesitan j − i cambios consecutivos de la fila i para
llevarla a la fila j y j − i − 1 cambios consecutivos de la fila j para llevarla a la fila i, por tanto
det(B) = (−1)j−i (−1)j−i−1 det(A) = (−1)2j (−1)−2i (−1)−1 det(A) = − det(A).
| {z } | {z } | {z }
=1
=1
=−1
De este resultado deducimos los siguiente.
Corolario 5.11. Sea A una matriz n × n y sea E la matriz elemental que se obtiene de In al intercambiar las
filas i y j entonces det(E) = −1 y det(EA) = det(E) det(A).
Demostración. Si E se obtiene al intercambiar las filas i y j de In , entonces por el teorema anterior tenemos
que det E = − det In = −1.
Por el Teorema 1.13 tenemos que EA es la matriz obtenida de A al intercambiar sus filas i y j, se sigue del
teorema anterior
det EA = − det A = det E det A.
Ahora demostramos un par de lemas necesarios para pasar al tercer tipo de matrices elementales.
Lema 5.12. Si A es una matriz n × n con dos filas iguales, entonces det(A) = 0.
167
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Demostración. Supongamos que las filas i y j de A son iguales y sea B la matriz que se obtiene de A al
intercambiar las filas i y j, entonces B = A. Ahora, por el Teorema 5.10 tenemos que det(B) = − det(A), por
tanto det(A) = − det(A), o equivalentemente, 2 det(A) = 0, concluimos que
det(A) = 0.
Lema 5.13. Sean A, B y C matrices cuyas filas son iguales excepto la fila i y


a11 · · · a1n
 .
.. 
..

 .
.
 .
. 




C es la suma de las filas i de A y B, es decir, A =  ai1 · · · ain , B =


 .
.. 
..

 ..
.
.


an1 · · · ann


a11
···
a1n


..
..
..


.


.
.




ai1 + bi1 · · · ain + bin , entonces det(C) = det(A) + det(B).




..
..
..


.
.
.


an1
···
ann
talque

a11
 .
 .
 .


 bi1

 .
 ..

an1
la i−ésima fila de

· · · a1n
.. 
..

.
. 


· · · bin  y C =

.. 
..
.
. 

· · · ann
Demostración. Primero nótese que para j = 1, . . . , n se tiene que Cij = Aij = Bij , ya que al eliminar la fila i
de A se obtiene la misma matriz que al eliminar la fila i de B y la misma matriz al eliminar la fila i de C, por
tanto al usar expansión por cofactores en la fila i de C obtenemos
det(C) =
n
X
k=1 a
=
n
X
k=1
cik (−1)i+k Cik =
|{z}
ik +bik
aik (−1)i+k Cik +
|{z}
Aik
= det(A) + det(B).
n
X
(aik + bik )(−1)i+k Cik =
k=1
k=1
n
X
k=1
n
X
bik (−1)i+k Cik =
|{z}
Bik
n
X
aik (−1)i+k Cik + bik (−1)i+k Cik
aik (−1)i+k Aik +
n
X
bik (−1)i+k Bik
k=1
k=1
Este lema se puede usar para reducir ciertos cálculos de determinantes como se muestra en el siguiente
ejemplo.

0




Ejemplo 5.6. Calcular el determinante de la matriz A = −1 1 2.


2 2 2
Solución. Escribimos las entradas de la segunda fila como una suma de dos números








3 2 0
3 2 0
3
2
0
3 2 0
















det(A) = det −1 1 2 = det 0 − 1 0 + 1 2 + 0 = det 0 0 2 + det −1 1 0 .








2 2 2
2 2 2
2
2
2
2 2 2

3
2
168
De esta forma obtenemos dos matrices ambas con una fila o una columna con 2 ceros, cuyos determinantes
calculamos usando expansión

3 2


det(A) = det 0 0

2 2
por dicha fila o


3
0




2 + det −1


2
2
columna y obtenemos:




2 0

3
3 2

2+3
 + (−1)3+3 2 det 
1 0 = (−1) 2 det 

−1
2 2
2 2

2

1
= −2(6 − 4) + 2(3 − (−2)) = −4 + 10 = 14.
Finalmente a pasamos a mostrar que al sumar un múltiplo de una fila a otra fila



a11
a11 · · · a1n





 ..
..
.
.
..
.. 

 .
.







 ai1 · · · ain 
ai1





 .
..
.
..
..  y sea B = 
.
Teorema 5.14. Considere la matriz A = 
.
.


 .



a + ca

a
 j1
 j1 · · · ajn 
i1



..
.. 

 ..
..

 .
.
.
. 



an1
an1 · · · ann
que se obtiene de A al sumar c veces la fila i a la fila j de A, entonces
el determinante se preserva.

···
a1n


..
..

.
.



···
ain


.
..
 la matriz
.
.
.


· · · ajn + cain 


..

..

.
.

···
ann
det(B) = det(A).
Demostración. Por el lema anterior tenemos que



a
a11
···
a1n

 11




.
.
..
..
..

 ..

.
.







 ai1

ai1
···
ain




 .

..
..
..

 ..
=
det
det(B) = det 
.
.
.







a
a + ca
· · · ajn + cain 
 j1
 j1
i1



..
..

 ..

..

 .

.
.
.



an1
an1
···
ann
|

a
···
 11
 ..
..
 .
.


 ai1 · · ·

 .
..
.
= det(A) + c · det 
.
 .

a
 i1 · · ·

 ..
..
 .
.

an1 · · ·
|
{z

a1n

.. 
. 


ain 

.. 
. 
 = det(A).

ain 


.. 
. 

ann
}
=0 (Lemma 5.12)
···
..
.
···
..
.
···
..
.
···
{z
A


a1n
a

 11
 ..
.. 
 .
. 





 ai1
ain 


 .
.. 
 ..
+
det
. 




ca
ajn 
 i1


.. 
 ..

 .
.


ann
an1
}
···
..
.
···
..
.
···
..
.
···

a1n

.. 
. 


ain 

.. 
. 


cain 


.. 
. 

ann
169
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Obtenemos el siguiente resultado.
Corolario 5.15. Sea A una matriz n × n y sea E la matriz elemental que se obtiene de In al sumar c veces la
fila i a la fila j de I entonces det(E) = 1 y det(EA) = det(E) det(A).
Demostración. Como E se obtiene de sumar un múltiplo de una fila a otra fila, tenemos por el teorema
anterior que det E = det In = 1.
Ahora, la matriz EA se obtiene de A al multiplicar la fila i por c, Teorema 1.13, se sigue por el teorema
anterior que
det(EA) = det A = det E det A.
Resumimos los resultados de la sección en el siguiente corolario.
Corolario 5.16. Sea A una matriz n × n y E una matriz elemental, entonces
det(EA) = det(E) det(A)
y
det(E) 6= 0.
Mas aún, si E1 · · · , Ek son matrices elementales, entonces
det(E1 · · · Ek A) = det(E1 ) · · · det(Ek ) det(A).
Demostración. El resultado se sigue por inducción y los corolarios 5.9, 5.11 y 5.15.
Los resultados de esta sección nos permiten usar operaciones elementales para calcular el determinante de
una matriz. La regla es simple: si intercambiamos dos filas, por el Teorema 5.10, el determinante de la nueva
matriz es menos el determinante de la anterior. Si sumamos un múltiplo de una fila a otra fila, por el Teorema
5.14, el determinante no cambia. En teorı́a estas dos operaciones son suficientes para el calculo del determinante
usando operaciones elementales, sin embargo el Teorema 5.8 nos permite factorizar una constante c en una fila
tal como se mostró en el Ejemplo 5.5. Para una mejor ilusatración presentamos los siguientes ejemplos.


0 3 1




Ejemplo 5.7. Usar operaciones elementales de fila para calcular el determinante de la matriz A = 0 2 3.


2 2 1
Solución. Para la reducción lo primero que se harı́a es intercambiar las filas 1 y 3, entonces por el Teorema
5.10 tenemos que

2 2 1





det A = − det 0 2 3 .


0 3 1
Lo siguiente para convertir la matriz en una matriz triangular superior debemos convertir el 3 en la posición 2, 3
de la matriz en un 0. Para esto podemos sumar −3/2 de la fila 2 a la fila 3. El Teorema 5.14 nos dice que esta
170

2
2 1


2 2
 

 

operación no cambia el determinante, por tanto el determinante de las matrices 0 2 3 y 0 2
 

0 0
0 3 1
(obtenida de la anterior al aplicar la operación de fila − 32 F2 + F3 → F3 ) son iguales. Por tanto




2 2
1
2 2 1








det A = − det 0 2 3 = − det 0 2
3  = −2 · 2 · (−7/2) = 14,




0 0 −7/2
0 3 1
1



3 

−7/2
este último resultado se obtiene del hecho que la matriz a la derecha es triangular superior y por tanto su
determinante es el producto de las entradas en la diagonal. Concluimos que det A = 14.


0 1
2




Ejemplo 5.8. En este ejemplo calculamos el determinante de la matriz A = 2 2 −2 de manera rápida,


3 3
2
solo se indica la operación que se hace, el teorema que se usa y el consecuente resultado.






2 2 −2
0 1
2
2 2 −2












=
− det 0 1
det A = det 2 2 −2 F1 ↔F2 |{z}
=
− det 0 1
2  − 32 F1 +F3 ↔F3 |{z}
2  = −10






Tma 5.10
Tma 5.14
3 3
2
3 3
2
0 0
5
También se pudo haber usado el Teorema 5.8 en el segundo paso como se indica a continuación, sin embargo
como se mencionó antes, es suficiente con los Teoremas 5.10 y 5.14 en todos los casos.






1 1 −1
2 2 −2
0 1
2












=
−2
det
=
− det 0 1
det A = det 2 2 −2 F1 ↔F2 |{z}


0 1
2
2


 |{z}



Tma 5.8
Tma 5.10
3 3
2
3 3
2
3 3
2


1 1 −1




−2
det
=

 = −2 · 1 · 1 · 5 = −10
0
1
2
|{z}


Tma 5.14
0 0
5
−3F1 +F3 ↔F3
Problemas
5.2.1. Use operaciones elementales de fila para calcular el determinante de las siguientes matrices







1 2 −1 3
0 2 −1



0 2 −1
1 2 3







2 2 −2 4
1 1 −1




 y D=
C=
B = 1 3 −2 ,
A =  4 5 4 ,







3 2 −1 0
2 1 −3



3 4 −3
3 2 1
2 3 −1 2
1 1 −1

4


1


1

2
5.2.2. Sea A una matriz de tamaño 3×3 invertible, si las operaciones elementales que se aplicaron a A para
llevarla a su forma escalonada reducida son 2F1 + F3 → F3 , 2F2 → F2 , F2 ↔ F3 y −F3 + F1 → F1 , calcule lo
siguiente
171
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
1. det A, usando las propiedades vistas en esta sección
2. la matriz A y caclule el determinante por cofactores.
3. La inversa de A y verifique que det A =
1
det A .
5.2.3. Si E ∈ Mn (R) es una matriz elemental, muestre que det E = det1 E .
 


F1
F1 + F3
 


 


5.2.4. Si A = F2  es una matriz con F1 , F2 y F3 las filas de A y det A = 3. Calcule det F1 + F2 .
 


F3
F2 + F3
5.2.5. Sea A una matriz n × n y c ∈ R. Muestre que det(cA) = cn det(A).
5.2.6. Si A es una matriz 3×3 con det A = −3 determine det( 12 A) y det(−A).
5.2.7. Si A es una matriz 4×4 y se sabe que det(2A) = 4, determine det(A) y det(−A).
5.2.8. En este problema se propone demostrar que las propiedades del determinante con respecto a operaciones
de fila también se cumplen en operaciones columna.
Sean v1 , . . . , vn , w ∈ Rn y sea A = [ v1 · · · vn ] la matriz cuyas columnas son los vectores v1 , . . . , vn y λ ∈ R.
Demuestre lo siguiente:
1. det[ v1 · · · λvi · · · vn ] = λ det A.
2. si i < j entonces det[ v1 · · · vj · · · vi · · · vn ] = − det A.
3. det[ v1 · · · vi · · · vi · · · vn ] = 0.
4. det[ v1 · · · vi + w · · · vn ] = det[ v1 · · · vi · · · vn ] + det[ v1 · · · w · · · vn ].
5. si i 6= j entonces det[ v1 · · · vi · · · vj λvi · · · vn ] = det A.
6. det[ λv1 · · · λvn ] = λn det A.
(Ayuda: Use el hecho que det A = det At .)
5.2.9. Sean A, B ∈ Mn (R) con B diagonal, demuestre que det(AB) = det A det B.
Muestre también que det(BA) = det B det A. (Ayuda: Use el Problema 1.2.13).
5.2.10. Si B es antisimétrica con n impar entonces det B = 0.


1+a
b
c




5.2.11. Muestre que det  a
1+b
c  = 1 + a + b + c.


a
b
1+c

1
c1
5.2.12. Sea A =  ..
.
n−1
Vandermonde.
c1
1
c2
···
···
1
cn
···
cn−1
n
.. . .
.
.
n−1
c2

.. . Demuestre que det A =
.
Y
i<j
(ci − cj ). A la matriz A se le llama matriz de
172
5.3.
Propiedades del determinante
En esta sección se demuestran dos propiedades importantes del determinante. La primera es que el producto
de los determinantes de éstas y la segunda dice que el determinante de la inversa una matriz es el inverso
multiplicativo del determinante de ésta. Tambiés se establece otra caracterización de matrices invertibles en
adición a las establecidas en el el Corolario 1.22.
Teorema 5.17. Sean A y B matrices n × n, entonces det(AB) = det A det B.
Demostración. Caso 1. Si A es invertible, entonces por el Teorema 1.17 A = E1 · · · Ek con E1 , . . . , Ek matrices
elementales. Entonces del Corolario 5.16 se tiene
det(AB) = det(E1 · · · Ek B) = det E1 · · · det Ek det(B)
{z
}
|
det(E1 ···Ek )
= det(E1 · · · Ek ) det B = det A det B.
| {z }
A
Caso 2. Si A no es invertible, entonces por el Teorema 1.15 A = E1 · · · Ek · A′ donde E1 , . . . , Ek son matrices
elementales y A′ es una matriz en forma escalonada reducida. Como A no es invertible, entonces rango(A) =
rango(A′ ) < n y como es una matriz cuadrada se debe dar que A′ tiene al menos una fila de ceros y por tanto
A′ B tiene una fila de ceros. Se sigue que det(A′ B) = 0 = det A′ y usando el Corolario 5.16 tenemos
det(AB) = det(E1 · · · Ek A′ B) = det E1 · · · det Ek det(A′ B) = 0,
| {z }
=0
y por otro lado tenemos que
′
det A det B = det(E1 · · · Ek A′ ) det B = det E1 · · · det Ek |det
{zA} det(B) = 0.
|
{z
}
=0
=det E1 ··· det Ek det A′
De las dos últimas ecuaciones tenemos que det(AB) = det(A) det(B).
En ambos casos obtenemos la fórmula deseada.
De los resultados obtenidos para matrices elementales obtenemos la siguiente caracterización de matriz invertible.
Teorema 5.18. Sea A una matriz n × n, entonces A es invertible si y sólo si det A 6= 0.
Demostración. “⇒” Supongamos que A es invertible, entonces A = E1 · · · Ek con E1 , . . . , Ek son matrices
elementales, entonces por el Corolario 5.16 tenemos que det E1 6= 0, , . . . , det Ek 6= 0. Usando de nuevo el
Corolario 5.16 tenemos que
det A = det(E1 · · · Ek ) = det E1 · · · det Ek 6= 0.
| {z } | {z }
6=0
6=0
“⇐” Supongamos que det A 6= 0 y supongamos por el absurdo que A no es invertible, entonces A = E1 · · · Ek ·A′
donde E1 , . . . , Ek son matrices elementales y A′ es una matriz en forma escalonada reducida. Como A no es
173
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
invertible, entonces rango(A) = rango(A′ ) < n y como es una matriz cuadrada se debe dar que A′ tiene al
menos una fila de ceros y por tanto det(A′ ) = 0, luego
′
det(A) = det(E1 · · · Ek A′ ) = det(E1 ) · · · det Ek |det
{zA} = 0,
{z
}
|
=0
det E1 ··· det Ek det A′
pero esto contradice la hipótesis. Por tanto A es invertible.
Terminamos la sección con el siguiente resultado que se sigue de lo anterior.
Corolario 5.19. Si A es una matriz invertible de tamaño n × n entonces det(A−1 ) =
1
.
det A
Demostración. Por el teorema anterior det A · det(A−1 ) = det(A · A−1 ) = det(I) = 1. Se sigue que
det(A−1 ) =
1
.
det A
Problemas

2 3


5.3.1. Sea A = 2 2

5 2

2


3, calcule det A, A−1 y verifique que det A−1 =

1
1
det A .
5.3.2. Sean A y B matrices cuadradas tal que det A = −1 y det AB = 2. Determine det B, det(B −1 ),
det (AB)−1 , det(A3 ) y det(AAt ).
5.3.3. Una matriz A ∈ Mn (R) se llama nilpotente si Ak = 0 para algún k ∈ Z≥0 . Muestre que si A es nilpotente
entonces det A = 0.
5.3.4. Demuestre que si B es una matriz ortogonal entonces det B = ±1.
5.3.5. Demuestre que si P es una matriz proyección, es decir P 2 = P , entonces det P = 0 o det P = 1.
5.3.6. Demuestre que si P es una matriz proyección entonces P = I si y sólo si det P = 1. (Ayuda: Use el
Problema 4.3.9 .)
5.3.7. Sean A, B ∈ Mn (R), demuestre que det(AB) = det(BA). Si A es invertible muestre que det(ABA−1 ) =
det B.
5.3.8. Demuestre que si A, B ∈ Mn (R) con n impar y AB = −BA entonces det A = 0 o det B = 0.
174
5.4.
Matriz Adjunta
En esta sección se define la matriz adjunta de una matriz A cuadrada. La principal motivación para definir
esta matriz es que la podemos usar para deducir una fórmula de la inversa de la inversa de A cuando A es
invertible. Si A no es invertible mostraremos que el producto de A por su adjunta es la matriz nula.
Definición 5.4. Sea A una matriz de tamaño n×n, definimos la matriz adjunta de A como la matriz definida
por

C11


 C21
Adj(A) = 
 ..
 .

Cn1
C12
···
C22
..
.
···
..
.
Cn2
···
donde Cij = (−1)i+j det(Aij ) es el ij-ésimo


1 2 3




Ejemplo 5.9. Sea A = 1 4 7, calcule


1 6 0
Solución. Los cofactores de A son

4
C11 = (−1)1+1 det 
6

1
C13 = (−1)1+3 det 
1

1
C22 = (−1)2+2 det 
1

2
C31 = (−1)3+1 det 
4
C1n
t

C11




C2n 
 C12
 =
.. 
 ..
 .
. 


Cnn
C1n
C21
···
C22
..
.
···
..
.
C2n
···
Cn1



Cn2 

..  ,
. 

Cnn
cofactor de A.
la matriz adjunta de A.
7
0
4
6
3
0
3
7

 = −42

=2

 = −3

=2

C12 = (−1)1+2 det 
1

2
C21 = (−1)2+1 det 
6

1
C23 = (−1)2+3 det 
1

1
C32 = (−1)3+2 det 
1

C33 = (−1)3+3 det 
Se sigue que la matriz adjunta está dada por:

C
C21
 11

adj(A) = C12 C22

C13 C23
C31
1

1 2
1 4



7
=7
0

3
 = 18
0

2
 = −4
6

3
 = −4
7
 = 2.
−42
 
 
C32  =  7
 
2
C33
18
−3
−4
2



−4 .

2
El siguiente lema es crucial para mostrar la fórmula de la inversa de una matriz invertible en términos de
la adjunta de A.
175
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO


a11 · · · a1n


.. 
 .
..
Lema 5.20. Sea A =  ..
entonces ai1 Cj1 + · · · + ain Cjn = 0 si 1 ≤ i 6= j ≤ n, donde Cik es el
.
. 


an1 · · · ann
ik-ésimo cofactor de A. Es decir, la expansión por cofactores en la fila j con coeficientes en otra fila i (i 6= j)
se anula.
Demostración.
Sea B una

 matriz con las mismas filas de A excepto la fila j en donde se repite la fila i, es
a
· · · a1n
 11

 ..
.. 
..
 .
.
. 




 ai1 · · · ain 


 .
.. 
.

.
.
decir B =  .
.
. 
. Nótese que para k = 1, . . . , n se tiene que Ajk = Bjk ya que al eliminar la j-ésima


a

 i1 · · · ain 


.. 
 ..
..
 .
.
. 


an1 · · · ann
fila de A se obtiene la misma matriz que al eliminar la j-ésima fila de B. Además el determinante de B es cero
por tener dos filas iguales. Entonces tenemos que
0 = det(B) = Expansión en cofactores de la fila j de B
=
=
n
X
aik (−1)j+k det(Ajk )
bjk (−1)j+k det(Bjk ) =
{z
}
|
|{z}
|{z}
k=1
k=1
n
X
n
X
k=1
aik
Cjk
Ajk
aik Cjk = ai1 Cj1 + · · · + ain Cjn .
A continuación se deduce una fórmula para la inversa de una matriz invertible usando la adj(A).
Teorema 5.21. Sea A una matriz de tamaño n × n, entonces
A · adj(A) = det(A) · I.
De esto se sigue que
1
adj(A),
det(A)
2. si A no es invertible entonces A · adj(A) = 0.



C11
a11 · · · a1n



.


 ..
..
..  y adj(A) =  ...
Demostración. Sea A =  .
.



C1n
an1 · · · ann
de A. Entonces llamando dij a la ij-ésima entrada de la matriz


0
dij = ai1 Cj1 + · · · + ain Cjn =

det(A)
1. si A es invertible entonces A−1 =

Cn1

.. 
, donde Cij es el ij-ésimo cofactor
. 

· · · Cnn
A · adj(A), tenemos que
···
..
.
si i 6= j (Lema 5.20),
si i = j (Teorema 5.3.)
176
Por tanto

d11
 |{z}
=det(A)


 d21
 |{z}

A · adj(A) =  =0
 .
 .
 .


dn1
 |{z}
d12
|{z}
···
=0
d22
|{z}
···
..
.
..
dn2
|{z}
···
=det(A)
=0
=0
.

d1n
|{z}  

=0 
 det(A)
d2n 

|{z} 
 0

=0  = 
 ..
.. 
  .
.  

0

dnn 
|{z}
0
···
0
det(A)
..
.
···
..
.
0
..
.
0
···
det(A)




 = det(A) · I.



(5.11)
=det(A)
Ahora, si A es invertible se tiene que det(A) 6= 0 y de la Ecuación (5.11) se sigue que A ·
1
adj(A) = I.
det(A)
Por tanto
A−1 =
1
adj(A).
det(A)
En el caso en que A no es invertible, tenemos que det(A) = 0 y la Ecuación (5.11) se convierte en A · adj(A) =
0.

1
2 3





Ejemplo 5.10. Sea A = 1 4 7 calcule el determinante de A y la inversa de A.


1 6 0
Solución. Por el ejemplo anterior sabemos que la matriz adjunta de A está dada por:

 

−42
18
2
C11 C21 C31

 


 

adj(A) = C12 C22 C32  =  7
−3 −4 .

 

2
−4
2
C13 C23 C33
El determinante de A lo calculamos por expansión por cofactores en la tercera fila, usando los cofactores C31 ,
C32 y C33 que se calcularon en el ejemplo anterior, tenemos que
det(A) = a31 C31 + a32 C32 + a33 C33 = 1 · 2 + 6 · (−4) + 0 · 2 = −22
Luego, la inversa de A está dada por
A−1 =

−42
1
−1 

adj(A) =
 7
det(A)
22 
2
18
−3
−4
2



−4 .

2
Problemas
5.4.1. Calcule la adjunta de las siguientes matrices

1


A = 4

3
2 3



5 4 ,

2 1

0


B = 1

3

2 −1


3 −2 ,

4 −3

1


2
C=

3

2
2 −1
2 −2
2 −1
3 −1

3


4


0

2

y
0


1
D=

2

1
2 −1
1 −1
1 −3
1 −1

4


1


1

2
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
177
Use los cálculos para determinar la inversa de las que son invertibles.
5.4.2. Sea A ∈ Mn (R) una matriz invertible y B = Adj(A),
1. demuestre que B −1 =
1
det A A,
2. demuestre que det B = (det A)n−1 ,
3. Si n = 4 y det B = 8 calcule det A.

2


4. Determine las posibles A tal que adj(A) = 2

3
3 2



2 3.

2 1
5. Demuestre que si n es impar entonces det(adj(A)) es positivo.
5.4.3. Sea A ∈ Mn (R) una matriz invertible. Demuestre que la matriz adj(A) es invertible y que adj(A)−1 =
adj(A−1 ).
5.4.4. Sea A ∈ Mn (R) una matriz no invertible y no nula, demuestre que adj(A) no es invertible y por tanto
det(adj(A)) = 0.

a11

 ..
5.4.5. Sea A =  .

an1
tomados de la columna

a1n

.. 
, demuestre que la expansión por cofactores en la columna j con coeficientes
. 

· · · ann
i, i 6= j, se anula. Es decir a1i C1j + · · · + ani Cnj = 0.
···
..
.
Use esto para demostrar que adj(A)A = det(A)I.
5.4.6. Si A es simétrica invertible entonces A−1 es simétrica. (Ayuda: Muestre que Aij = Atji .)
5.4.7. Sea A ∈ Mn (R), demuestre que Col(A) ⊆ N ul(adj(A)) y Col(adj(A)) ⊆ N ul(A).
Deduzca que rango(A) + rango(adj(A)) ≤ n.
5.4.8. A ∈ Mn (R) con rango(A) = n − 1, muestre que rango(adj(A)) = 1.
5.5.
La Regla de Cramer
En esta sección corta se presenta el resultado conocido como la regla de Cramer. Este método da una fórmula
para calcular la solución a un sistema con solución única, cuando la solución no es única no se puede aplicar
este método. El método es además computacionalmente ineficiente, lo que lo hace poco útil. Tal vez el método
pueda servir en el caso en que no se necesite el valor de todas la incognitas en un sistema, como es el caso en
el Problema 5.5.2. La sección puede ser obviada y la hacemos solo por mostrar la demostración del método para
los lectores que les resulte interesante.
178
Teorema 5.22. (Regla de Cramer) Sea Ax = b un sistema de ecuaciones con A una matriz n × n invertible.
Sea A = [ C1 · · · Cn ] con C1 , . . . , Cn las columnas de A y para i = 1, . . . , n definimos Ai como la matriz que
se obtiene al reemplazar la i-ésima columna de A por el vector b. Es decir,
A1 = [ b C2 · · · Cn ],
A2 = [ C1 b · · · Cn ],
...,
An = [ C1 C2 · · · b ].
Entonces la solución única al sistema está dada por
det(A1 )
,
det(A)
det(A2 )
det(An )
, . . . , xn =
.
det(A)
det(A)
 
x1
 
 .. 
Demostración. El sistema tiene solución única única x =  . , esto lo garantiza el Teorema 1.12 porque A
 
xn
es invertible. Entonces
 
x1
h
i 
 .. 
b = Ax = C1 · · · Cn  .  = x1 C1 + · · · + xn Cn .
 
xn
x1 =
x2 =
Ahora, para 1 ≤ i ≤ n fijo, por las propiedades del determinante enunciadas en el Problema 5.2.8 se tiene que:
h
det(Ai ) = det C1
h
= det C1
h
= det C1
···
b
···
Cn
i
i
x 1 C1 + · · · + x n Cn · · · Cn
i
h
· · · x1 C1 · · · Cn + · · · + det C1 · · · xi Ci · · ·
h
i
+ · · · · · · + det C1 · · · xn Cn · · · Cn
h
i
h
=x1 det C1 · · · C1 · · · Cn + · · · + xi det C1 · · · Ci · · ·
|
{z
}
{z
|
···
=A
=0 (por columna repetida)
h
+ · · · · · · + xn det C1
|
···
Cn
{z
···
Cn
=0 (por columna repetida)
=xi det(A).
Al despejar xi de esta ecuación obtenemos xi =
i
Cn
i
Cn
i
}
}
det(Ai )
.
det(A)
3x + 2y − z = 0
Ejemplo 5.11. Resolver el sistema −x
x
+ 3z = 0 usando la regla de Cramer.
+ z=1

3


Solución. Primero escribimos el sistema en la forma Ax = b con A = −1

1
necesitamos los determinantes de las matrices de A1 , A2 , A3 y A.
 
0
 

 

3  y b = 0 . Después
 

1
1
2 −1
0
0

179
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

0 2
3
0


det(A1 ) = det 0 0

1 0



det(A2 ) = det −1 0

1 1

3


det(A3 ) = det −1

1




−1

2
−1

=6
3  = 1 det 

0
3
1



−1

3 −1

 = −8
3  = −1 det 

−1
3
1
2 0



−1

0 0 = −2 det 

1
0 1

0
=2
1



3 2 −1


−1 3


=8
det(A) = det −1 0
3  = −2 det 


1 1
1 0
1
Por tanto, por la Regrla de Cramer, la solución al sistema está dada por
x=
6
3
det(A1 )
= =
det(A)
8
4
y=
det(A2 )
−8
det(A3 )
2
1
=
= −1 y z =
= = .
det(A)
8
det(A)
8
4
Problemas
5.5.1. Use el método de Cramer

2 1


a. A = 1 2

0 1
para calcular la solución al sistema Ax = b si


 

1 2 0
1
0


 



 

b. A = 0 1 1
1 y b = 2


 

1 0 1
3
2
5.5.2. Determine el valor de y en la solución al sistema
5.6.



x + y + z + 2t = 0






x +
z+t=1
y
 
1
 
 
b = 2
 
1
.



y+z+t=0





x + y + z + t = 0
Interpretación Geométrica del Determinante
En esta sección le daremos una interpretación geométrica al determinante. Veremos como usarlo para calcular
volúmenes de paralelepı́pedos en cualquier dimensión. También mostraremos como el proceso de Gramm-Schmidt
puede ser útil para el mismo objetivo. Comenzamos con la siguiente definición.
180
Definición 5.5. Si se tienen dos vectores v1 , v2 ∈ R2 , se define el paralelogramo determinado por v1 y v2 ,
como el paralelogramo con vértices en los extremos de los vectores v1 , v2 y v1 + v2 y en el origen.
Similarmente, se define el paralelepı́pedo determinado por los vectores v1 , v2 , v3 ∈ R3 como el paralelepı́pedo con vértices en los extremos de los vectores v1 , v2 , v3 , v1 + v2 , v1 + v3 , v2 + v3 , v1 + v2 + v3 y en el
origen.
v2 + v3
v1 + v2
v2
v3
b
Paralelogramo determinado
por v1 y v2
v1 + v3
v2
v1
O
v1 + v2 + v3
O
b
v1 + v2
v1
Paralelepı́pedo determinado por v1 , v2 y v3
En general el n-pı́pedo determinado por n vectores en Rn es el n-pı́pedo con vértices en los extremos de
los 2n vectores vi1 + · · · + vik con k entre 1 y n y el origen. Es decir, los vértices del paralelepı́pedo n-dimensional
son el origen y los extremos de todos los vectores que se son sumas de k de los vectores originales, con k variando
de 1 a n.
El siguiente resultado es el más importante de la sección. En éste se establece la relación entre el volumen
del n-pı́pedo determinado por n vectores en Rn y el determinante de la matriz que estos forman. De esta forma,
el teorema provee una interpretación geométrica del determinante.
Teorema 5.23. Sean v1 , . . . , vn ∈ Rn n vectores linealmente independientes y sea A = [ v1 . . . vn ] la matriz
cuyas columnas son los vectores v1 , . . . , vn . Entonces para n ≥ 3 tenemos que
| det A| = volumen del paralelepı́pedo n − dimensional determinado por los vectores v1 , . . . , vn .
Las barras denotan el valor absoluto de det A.
En el caso n = 2 se tiene que | det A| = área del paralelogramo determinado por v1 y v2 .
La demostración se hará al final de la sección.
 
 
2
1
Ejemplo 5.12. Sean v1 =   y v2 =  . Por el teorema anterior tenemos que el área A del paralelogramo
−2
2
determinado por v1 y v2 está dada por


h
i 1
2 = | − 2 − 4| = | − 6| = 6.


A = det v1 v2 = det
2 −2
Más especificamente el paralegramo tiene un área de 6 unidades cuadradas.
 
 
 
0
2
0
 
 
 
 
 
 
Ejemplo 5.13. Sean v1 = 2, v2 = 1 y v3 = 2, calcular el volumen del paralelepı́pedo determinado por
 
 
 
3
0
2
estos vectores.
181
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Solución. Sea V el volumen de este paralelepı́pedo,

0 2

h
i

V = | det v1 v2 v3 | = 2 1

3 0
En este caso el resultado es 4 unidades cúbicas.
de acuerdo al Teorema 5.23 tenemos que


0 
 2
2
 
= | − 2(4 − 6)| = 4.

=
−2

2
 3 2 2 En general, si tenemos k vectores v1 , . . . , vk linealmente independientes en Rn , el paralelepı́pedo determinado
por estos vectores, es un paralelepı́pedo k dimensional en Rn . El siguiente resultado nos da una fórmula para
calcular el volumen de este paralelepı́pedo.
Teorema 5.24. Sean v1 , . . . , vk vectores linealmente independientes en Rn y sea A = [ v1 · · · vk ] la matriz formada por estos vectores. El volumen V del paralelepı́pedo k dimensional determinado por los vectores v1 , . . . , vk
está dado por
V = ||w1 || · · · ||wk || = (q1 · v1 ) · · · (qk · vk ),
donde w1 , . . . , wk son los vectores ortogonales que se obtienen al aplicar el proceso Gramm-Schmidt a los vectores
v1 , . . . , vk y q1 , . . . , qk son los correspondientes vectores ortonormales obtenidos de normalizar los wi′ s.
Demostración. Procedemos de manera inductiva. Si k = 2 tenemos que w1 = v1 y w2 es perpendicular a v1
y, de acuerdo al proceso Gramm-Schmidt, w2 = v2 − proyv1 v2 es perpendicular a v1 . Más aún, como proyv1 v2
es el múltiplo de v1 más cercano a v2 tenemos que w2 es la altura del paraleogramo formado por v1 y v2 :
w2
v2
||w2 ||
v1 = w1
Se sigue que el área del paralelogramo determinado por v1 y v2 = |{z}
base × altura
| {z } = ||w1 || ||w2 ||.
=||w1 ||
=||w2 ||
Si k = 3, tenemos que w3 = v3 − proygen{v1 ,v2 } v3 es perpendicular al plano generado por v1 y v2 y además
la magnitud de este vector es la altura del paralelepı́pedo formado por v1 , v2 y v3 . Esto ya que el vector
proygen{v1 ,v2 } v3 es el vector en el subespacio gen{v1 , v2 } más cercano a v3 . Nótese además que la base de este
paralelepı́pedo es el paralelogramo formado por los vectores v1 y v2 y por el caso anterior tenemos que el área
de la base es ||w1 || ||w2 ||.
w3
v3
||w3 ||
v2
O
b
v1
182
Entonces tenemos que el volumen V de este paralelepı́pedo determinado por v1 , v2 y v3 está dado por
V = |área de{zla base} × |altura
{z } = ||w1 || ||w2 || ||w3 ||.
=||w1 || ||w2 ||
=||w3 ||
En el caso general se observa que wk es la altura del paralelepı́pedo (k − 1)-dimensional determinado por los
vectores v1 , . . . , vk−1 , con volumen ||w1 || · · · ||wk−1 || y por tanto el volumen V del paralelepı́pedo formado por
los k vectores está dado por
V = área de la base × altura = ||w1 || · · · ||wk−1 || ||wk ||.
Para terminar la demostración veamos que para cada i = 1, . . . k se tiene que ||wk || = qi · vi . Para esto es
suficiente notar que el ángulo θ formado por wi y vi es el mismo ángulo entre qi y vi . Esto ya que qi ||w1i || wi es
múltiplo de wi .
wi
vi
θ
qi
b
O
El triángulo en esta figura es un triángulo rectángulo, entonces se tiene además que cosθ =
adyacente
hipotenusa
=
||wi ||
||vi || .
Por tanto
||wi ||
= ||wi ||.
qi · vi = ||qi || ||vi ||cosθ = ||vi ||cosθ = ||vi ||
|{z}
||vi ||
=1
Concluimos que el volumen V del paralelepı́pedo formado por los vectores v1 , . . . , vk está dado por
V = ||w1 || · · · ||wk || = (q1 · v1 ) · · · (qk · vk ).
Observación 5.2. Si v1 , . . . , vk son vectores linealmente independientes en Rn , A = [ v1 · · · vk ] y A = QR
es la descomposición QR de la matriz entonces el volumen V del paralelepı́pedo determinado por los vectores
v1 , . . . , vk está dado V = | det R|.

q1 · v 1

 ..
Esto se sigue del hecho que R =  .

0
···
..
.
···

q1 · v k

.. 
.
. 

qk · v k
Ejemplo 5.14. Determine el volumen V del paralelepı́pedo en R4 determinado por los vectores v1 = (1, 1, 0, 0)
v2 = (0, 1, 1, 0) y v3 = (1, 0, 0, 1).
Solución. En el Ejemplo 4.33 calculamos que los vectores q1 , q2 y q3 están dados por




 
1
 √2 
 
 √1 
2
q1 = 
 ,
0
 
0
√1
1
√
− 6 


 √1 
6 

q2 = 

 √2 
 6 
0
y
 12 


− √1 
12 

q3 = 

 √1 
 12 
√3
12
183
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Se calculo además que q1 · v1 =
√2 ,
2
q2 · v 2 =
√3
6
√4 .
12
y q3 · v 3 =
Por tanto el volumen V está dado por
2 3 4
V = (q1 · v1 )(q2 · v2 )(q3 · v3 ) = √ √ √ = 2.
2 6 12
Es decir, paralelepı́pedo tiene un volumen de dos unidades cúbicas.
 
 
1
−2
 
 
 
 
Ejemplo 5.15. Sean v1 =  3  y v2 = 4 vectores en R3 , determine el área del paralelogramo en R3
 
 
4
3
determinado por estos vectores.
Solución. Necesitamos calcular los vectores ortonormales q1 y q2 que se obtienen al aplicar el proceso GrammSchmidt a los vectores v1 y v2 .
   
 
3
−2
1
   
 
  22    
v2 ·v1
Primero hacemos w1 = v1 y w2 = v2 − proyv2 v1 = v2 − v1 ·v1 v1 = 4 − 22  3  = 1 .
   
 
1
3
4
 
 
−2
3
 
 




Normalizando los vectores w1 y w2 obtenemos q1 = √122  3  y q2 = √111 1 .
 
 
3
1
Tenemos que el área A del paralelogramo es
√
1
1
A = (q1 · v1 )(q2 · v2 ) = √ 22 √ 10 = 10 2 ≈ 14,1.
22
11
Observación 5.3. La Proposición 5.24 también se puede usar para calcular áreas de triángulos en Rn como
se describe a continuación. Si A, B y C tres puntos no colineales en Rn , definimos v1 como el vector cuyas
coordenadas son las entradas del punto A − C y v2 el vector el vector cuyas coordenadas son las entradas del
a1 − c 1


 .. 
punto B − C. Es decir, si A = (a1 , . . . , an ), B = (b1 , . . . , bn ) y C = (c1 , . . . , cn ) entonces v1 =  .  y


an − c n


b1 − c 1


 . 
v2 =  .. . Para el área del triángulo simplemente notamos que


bn − c n
área del triángulo ABC =
1
área del paralelogramo determinado por v1 y v2 .
2
b
C
A
b
b
v1
O
b
v2
B
184
Ejemplo 5.16. Sean A = (−1, 2, 3), B = (2, 3, 4) y C = (1, −1, 0) en R3 , calcular el área del triángulo ABC.
Solución: El vector v1 tiene por coordendas las entradas del punto A menos las entradas del punto C y el

−2
 
 
vector v2 tiene por coordendas las entradas del punto B menos las entradas del punto C. Es decir, v1 =  3 
 
3
 
1
 
 
y v2 = 4.
 
4
√
En el Ejemplo 5.15 se calculó que el área del paralelogramo determinado por estos dos vectores es 10 2
unidades cuadradas, por tanto:
área del triángulo ABC =
√
1
1 √
área del paralelogramo determinado por v1 y v2 = 10 2 = 5 2 ≈ 7,0,7
2
2
Similarmente se puede calcular el volumen de una piramide en Rn dados 4 puntos no co-planares. Ver
Problema 5.6.5.
Finalizamos la sección con la demostración del Teorema 5.23.
Demostración del Teorema 5.23. Sea A = [ v1 · · · vn ] y sean Q y R tal que A = QR es la descomposición
QR de la matriz. Entonces Q es ortogonal cuadrada y por tanto Qt = Q−1 o equivalentemente Qt Q = I. Se
sigue que
1 = det I = det Qt Q = det Qt det Q = det Q det Q = (det Q)2 .
Se deduce que det Q = ±1, luego | det Q| = 1. Por la Observación 5.2 tenemos que el volumen V del parale-
lepı́pedo n dimensional determinado por los vectores v1 , . . . , vn está dado por V = | det R|. Tenemos entonces
que
| det A| = | det Q det R| = | det Q| | det R| = | det R| = V.
| {z }
=1
Concluimos que dicho volumen está dado por V = | det A| = | det[ v1 · · · vn ]|.
 
 
 
−1
2
1
 
 
 
 
 
 
−1
 1
2
 
 

Ejemplo 5.17. (Matlab) Sean v1 = 
 , v 2 =  , v 3 =   y v 4 =
−2
 0
3
 
 
 
2
2
0
paralelepı́pedo 4-dimensional formado por estos vectores.
 
0
 
 
2
 , calcular el volumen del
 
2
 
0
h
Solución. Para calcular el volumen necesitamos calcular el determinante de la matriz A = v1
el cual calculamos usando Matlab
v2
v3
v4
i
>> A = [1, 2, −1, 0; 2, 1, −1, 2; 3, 0, −2, 2; 0, 2, 2, 0]; det(A)
el resultado que se obtiene en este caso es que det A = −12. Por tanto el volumen V del paralelepı́pedo es
V = | − 12| = 12.
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
185
Problemas
5.6.1. Calcule el área del paralelogramo determinado por el par de vectores dados
 
 
 
 
−4
1
1
3
b. v1 =   y v2 =   .
a. v1 =   y v2 =   .
1
1
4
2
5.6.2. Calcule el volumen del paralelepı́pedo determinado por los vectores dados
 
 
 
 
 
 
3
1
1
1
2
−4
 
 
 
 
 
 
 
 
 
 
 
 
a. v1 = 1 , v2 = 3 y v3 = 1 .
b. v1 = 1 , v2 = 1 y v3 =  1  .
 
 
 
 
 
 
1
1
3
1
0
−1
5.6.3. Considere los vectores v1 , v2 , v3 , v4 y v5 en R5 con coordenadas (1, −4, 2, 2, 3), (1, 1, 1, 1, 2), (1, 0, 0, 4, 1),
(1, 3, 1, 5, 0) y (1, 0, 0, −1, 2), respectivamente. Calcule lo siguiente:
1. el volumen del paralelepı́pedo 5-dimensional determinado por v1 , v2 , v3 , v4 y v5 ,
2. el volumen del paralelepı́pedo 4-dimensional determinado por los vectores v1 , v2 , v3 y v4 ,
3. el volumen del paralelepı́pedo 3-dimensional determinado por los vectores v1 , v2 y v3 ,
4. el área del paralelogramos determinado por los vectores v1 y v2
5.6.4. Determine el área del triángulo determinado por los puntos:
1. A : (1, 0, 1), B : (1, 3, 1) y C : (1, 2, 3) en R3 .
2. A : (1, 0, 0, 1), B : (1, 3, 1, 0) y C : (1, 0, 0, −1) en R4 .
3. A : (1, 0, 0, 4, 1), B : (1, 3, 1, 5, 0) y C : (1, 0, 0, −1, 2) en R5 .
5.6.5. Sean A = (2, 1, 3, 4, 1, 0), B = (1, 1, 1, 1, 0, 1), C = (3, 5, 0, 0, 1, 1) D = (1, 2, 3, 4, 5, 6). Calcule el volumen
de la piramide en R6 con vértices en los puntos A, B, C, D. Ayuda: Defina los vectores v1 , v2 y v3 con coordenadas
A−D, B −D y C −D, respectivamente. Calcule al volumen del paralelepı́pedo determinado por estos tres vectores
y note que el volumen de la piramide es 1/6 del volumen del paralelepı́pedo.
5.6.6. Sean A : (α1 , . . . , αn ), B : (β1 , . . . , βn ) y C : (γ1 , . . . , γn ) tres puntos en Rn y sean v1 y v2 los vectores
con coordenadas (α1 − γ1 , . . . , αn − γn ) y (β1 − γ1 , . . . , β1 − γn ), respectivamente. Demuestre que los puntos A,
B y C son colineales si y sólo si det[ v1 v2 ] = 0. (Un conjunto de puntos es colineal si existe una lı́nea que los
contiene.)
5.6.7. Sean A : (α1 , . . . , αn ), B : (β1 , . . . , βn ), C : (γ1 , . . . , γn ) y D : (δ1 , . . . , δn ) cuatro puntos en Rn y sean
v1 , v2 y v3 los vectores con coordenadas (α1 − δ1 , . . . , αn − δn ), (β1 − δ1 , . . . , β1 − δn ) y (γ1 − δ1 , . . . , γn − δn ),
respectivamente. Demuestre que los puntos A, B, C y D son coplanares si y sólo si det[ v1 v2 v3 ] = 0. (Un
conjunto de puntos es coplanar si existe un plano que los contiene.)
186
Capı́tulo 6
Valores y Vectores Propios
En este capı́tulo estudiaremos los valores y vectores propios de una matriz. Este tópico es uno de los más
importantes en el álgebra lineal y tal vez el que tiene más aplicaciones conocidas dentro de las matemáticas y a
otras áreas. El objetivo principal es estudiar la diagonalización de matrices y los criterios para que una matriz
sea diagonalizable. Dado que los valores propios de una matriz son las raı́ces del polinomio caracterı́stico, todas
las matrices en este capı́tulo se tomarán con entradas en C, el conjunto de los números complejos, debido a que
a cada matriz le asociaremos un polinomio, cuyas raı́ces juegan un papel importante en la teorı́a y necesitamos
garantizar que el polinomio de grado n tiene exactamente n raı́ces contando multiplicidades.
6.1.
Polinomio Caracterı́stico
En esta sección se introducen los conceptos de polinomio caracterı́stico, valores propios, vectores propios y
subespacios propios de una matriz. También se definen las multiplicidades algebraica y geométrica de un valor
propio. Veremos que los valores propios son las raı́ces del polinomio caracterı́stico y demostraresmos algunas
propiedades de de los valores propios y vectores propios. Comenzamos con el siguiente lema del cual se sigue la
definición de polinomio caracterı́stico.
Lema 6.1. Sea A ∈ Mn (C) e I la matriz identidad, entonces det(A − xI) es un polinomio en x de grado n. El
coeficiente del monomio xn en este polinomio es (−1)n .
Demostración. Procedemos por inducción sobre n siendo el caso n = 1 inmediato.
Para k < n y toda B ∈ Mk (C), supongamos que det(B − xI) es un polinomio de grado k y que (−1)k es el
coeficiente de xk .
Sean aij (i, j = 1, . . . , n) las entradas de A y sea C = A − xI. Aplicando cofactores en la primera fila de
A − xI tenemos que
det(A − xI) = det C = (a11 − x) det C11 + · · · + (−1)1+n a1n det C1n ,
187
(6.1)
188
donde C1i (i = 1, . . . , n) es la matriz que se obtiene después de eliminar la fila 1 y la columna i de C.
Es fácil ver que C11 = A11 − xI, donde A11 es la matriz que se obtiene después de eliminar la fila 1 y la
columna 1 de A. Se sigue por inducción que det C11 = (−1)n−1 xn−1 + términos de grado menor a n − 1.
Por otra parte, aplicando cofactores en la fila i de C1i , para i = 2, . . . , n, se tiene que det C1i = (−1)n−2 xn−2 +
términos de grado menor a n − 2. Por tanto, de (6.1) tenemos que
det(A − xI) = (a11 − x) (−1)n−1 xn−1 + términos de grado menor a n − 1
+ otros términos de grado menor a n − 2
= (−1)n xn + términos de grado menor a n.
.
Definición 6.1. Sea A ∈ Mn (C) una matriz, al polinomio det(A − xI) se le llama el polinomio caraterı́stico de
A y éste será denotado por pA (x).

Ejemplo 6.1. El polinomio caraterı́stico de la matriz A = 

pA (x) = det(A − xI) = det 
1−x
1
2
−x

1
2

1
 es el polinomio:
0
 = (1 − x)(−x) − 2 = x2 − x − 2.
La razón por la cual en esta sección estamos considerando matrices con entradas en los complejos, es con el
fin de poder usar el Teorema fundamental de álgebra, el cual dice que todo polinomio de grado n con coeficientes
en los complejos, tiene exactamente n raı́ces contando multiplicidades. Por lo tanto para toda matriz compleja,
su polinomio caraterı́stico tiene n raı́ces. Estas raı́ces juegan un papel importante en la matriz A, ya que estas
coinciden con los valores propios de A. Esto lo mostraremos en el siguiente lema, después de definir valor propio
de una matriz.
Definición 6.2. Sea A ∈ Mn (C), decimos que λ ∈ C es un valor propio de A si existe un vector v 6= 0 tal que
Av = λv. En este caso decimos también que v es un vector propio de valor propio λ.
Lema 6.2. Sea A ∈ Mn (C), tenemos las siguientes caracterizaciones de valor propio para A.
λ ∈ C es un valor propio de A si y sólo si N ul(A − λI) 6= 0 si y sólo si λ es una raı́z de pA (x).
Demostración. Esto lo podemos ver por equivalencias como sigue.
λ es un valor propio de A si y sólo si existe v 6= 0 tal que Av = λv
si y sólo si existe v 6= 0 tal que (A − λI)v = 0
si y sólo si existe v 6= 0 tal que v ∈ Nul(A − λI)
si y sólo si A − λI no es invertible (Por el Corolario 1.22)
si y sólo si 0 = det(A − λI) = pA (λ) (Por el Teorema 1.22)
si y sólo si λ es un raı́z de pA (x).
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
189
Sea A ∈ Mn (C), si λ es un valor propio de A, los vectores propios de valor propio λ forman un subespacio
de Cn . Además éste espacio coincide con N ul(A − λI).
Lema 6.3. Sea λ ∈ C, tenemos lo siguiente
1. el conjunto E(λ) = {v ∈ Cn | Av = λv} es un subespacio de Cn .
2. E(λ) = N ul(A − λI) y se tiene además que E(λ) 6= {0} si y sólo si λ es un valor propio.
Demostración. Le demostración de este hecho es fácil y lo dejamos como ejercicio.
Definición 6.3. Si λ ∈ C es un valor propio, al subespacio E(λ) = N ul(A − λI) lo llamaremos el subespacio
propio de valor propio λ.
Del Lema 6.2 se deduce el siguiente procedimiento para calcular los valores y vectores propios de una matriz.
Procedimiento 6.1. (Procedimiento para calcular los valores y vectores propios)
1. Se calcula el polinomio caracterı́stico pA (x) = det(A − xI),
2. Se resuelve la ecuación pA (x) = 0, cuyas raı́ces corresponden a los valores propios.
3. Para cada valor propio λ encontrado en en el paso anterior, se calcula una base para N ul(A − λI). Los vectores
en dicha base son vectores propios de valor propio λ.


−3 5
, calcular los valores y vectores propios de A y determine los subespacios
Ejemplo 6.2. Sea A = 
−2 4
propios.
Solución. El polinomio caracteristico de A, está dado por


−3 − x
5
 = x2 − x − 2 = (x − 2)(x + 1).
pA (x) = det(A − xI) = det 
−2
4−x
Después se resuelve la ecuación pA (x) = (x − 2)(x + 1) = 0, cuyas soluciones son x = 2 y x = −1. Tenemos
por tanto para A dos valores propios: λ1 = 2 y λ2 = −1.
Ahora se calulan bases para N ul(A − λi I) con i = 2 e i = −1.



Para λ1 = 2 tenemos que N ul(A − 2I) = N ul 
1 −1
0
0

. De esto se sigue que
−5 5
−2 2
, cuya forma escalonada reducida está dada por
 
   
 
1
y
x
x
  ∈ N ul(A − 2I) si y sólo si x = y si y sólo si   =   = y   .]
1
y
y
y
190
 
1
Concluimos que v1 =   es un vector propio de valor propio λ1 = 2.
1

Ahora calculamos N ul(A − λ2 I) con λ2 = −1. Es decir, N ul(A + I) = N ul 

reducida de esta matriz está dada por 
1
−5/2
0
0

−2 5
−2 5

. La forma escalonada
. Por tanto tenemos que
 
 
   
5
5
x
y
x
  ∈ N ul(A + I) si y sólo si x = 5 y si y sólo si   =  2  = y  2  .
2
y
1
y
y
 
5
Se sigue que v2 =  2  es un vector propio de valor propio λ2 = −1.
1
En conclusión
la
matriz
λ1=2y λ2 = −1 y los correspondientes subespacios propios


 tiene valores propios
5 



1
son E(2) = gen v1 =   y E(−1) = gen v2 =  2  .


1 
1 
b
Observación 6.1. Es importante notar que los subespacios propios son subespacios invariantes bajo una trans-
formación lineal. En el ejemplo anterior si consideramos la transformación T definida por T (v) = Av, entonces
los subespacios E(2) y E(−1) son invariantes bajo T
E(2)
+
T (E(2) )
+
T
+
T (v1 )
+
v1
+
+
E(−1)
T (E(−1) )
v2
+
+
+
b
O
+
+
+
+
+
+
b
O
T (v2 )
+
+
+
+
+
+
+
+
+
Los vectores en la lı́nea E(−1) son enviados por T a la misma lı́nea. Más especificamente, para v ∈ E(−1) ,
T (v) = Av = −v, esto por ser un vector de valor propio −1. Similarmente, vectores en la lı́nea E(2) son
enviados por T a la misma lı́nea y en este caso para v ∈ E(2) se tiene que T (v) = Av = 2v por ser un vector de
valor propio 2. También se sigue del Lema 6.2 que las lı́neas E(−1) y E(2) son las únicas lı́neas invariantes bajo
multiplicación por la matriz A.
El hecho de que en general los subespacios propios E(λ) son invariantes bajo multiplicación por la matriz A es
fácil de ver. De hecho si v ∈ E(λ) entonces Av = λv, y como E(λ) es un subespacio, se sigue que Av = λv ∈ E(λ) .
Por tanto A(E(λ) ) ⊆ E(λ) .
191
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
En el ejemplo anterior también se puede verificar que los vectores propios encontrados son linealmente
independientes. Esto no es una casualidad, de hecho vectores propios correspondientes a valores propios distintos
son linealmente independientes.
Teorema 6.4. Sea A ∈ Mn (C) y sean v1 , . . . , vk vectores propios con valores propios λ1 , . . . , λk , respectivamente. Si los λi son diferentes entre sı́ entonces los vectores v1 , . . . , vk son linealmente independientes.
Demostración. Procedemos por inducción sobre k.
Si k = 2 vamos a demostrar que v1 y v2 son LI. Para esto supongamos que existen escalares α1 y α2 tal que
α1 v 1 + α2 v 2 = 0
(6.2)
multiplicando por A ambos lados obtenemos α1 Av1 +α2 Av2 = 0, equivalentemente
|{z}
|{z}
λ1 v 1
λ2 v 2
α1 λ1 v1 + α2 λ2 v2 = 0.
(6.3)
Ahora, multiplicando la Ecuacion (6.2) por λ1 obtenemos
α1 λ1 v1 + α2 λ1 v2 = 0.
(6.4)
Restando la Ecuación (6.4) de la Ecuación (6.3) tenemos que α2 (λ1 − λ2 )v2 = 0. Pero como λ1 6= λ2 , es decir,
λ1 − λ2 6= 0 y v2 6= 0 entonces se debe dar que α2 = 0. Reemplazando este valor en la Ecuación (6.2) tenemos
que α1 v1 = 0 y como v1 6= 0 se debe dar que α1 = 0. Por tanto v1 y v2 son linealmente independientes.
Ahora supongamos por inducción, que k − 1 vectores propios correspondientes a k − 1 valores propios distintos
son LI y mostremos que v1 , . . . , vk son LI. Para esto supongamos que
α1 v1 + · · · + αk vk = 0,
multiplicando por A ambos lados tenemos que α1 Av1 + · · · + αk Avk = 0 o equivalentemente
|{z}
|{z}
λ1 v1
(6.5)
λk vk
α1 λ1 v1 + · · · + αk λk vk = 0.
(6.6)
Ahora, multiplicando a ambos lados de la Ecuación (6.5) por λk tenemos
α1 λk v1 + · · · + αk λk vk = 0.
(6.7)
Restando la Ecuación (6.7) de la Ecuación (6.6)obtenemos
α1 (λ1 − λk )v1 + · · · + αk−1 (λk−1 − λk )vk−1 = 0.
Por hipótesis los vectores v1 , . . . , vk−1 son k − 1 vectores propios correspondientes a distintos valores propios y
por tanto son LI. Se sigue entonces que
α1 (λ1 − λk ) = · · · = αk−1 (λk−1 − λk ) = 0
| {z }
| {z }
6=0
6=0
192
como λ1 − λk 6= 0, · · · , λk−1 − λk 6= 0 se debe dar que α1 = · · · = αk−1 = 0. Reemplazando estos valores en la
Ecuación (6.5) obtenemos αk vk = 0 y como vk 6= 0 se sigue que αk = 0. Concluimos que los vectores v1 , . . . , vk
son LI.

5
6


Ejemplo 6.3. (MatLab) Calcule los valores y vectores propios de la matriz A = −3 −4

0
0
Solución. Calculamos el polinomio caracterı́stico con MatLab como sigue
9



−9.

2
>> A = [5 6 9; −3 − 4 − 9; 0 0 2]; p = poly(sym(A))
p =
x3 − 3 ∗ x2 + 4
para calcular los valores propios podemos factorizar p, lo cual podemos hacer con MatLab como sigue
>> factor(p)
ans =
(x + 1) ∗ (x − 2)2
De donde tenemos que los valores propios son λ1 = −1 de multiplicidad 1 y λ2 = 2 de multiplicidad 2.
Ahora para cada valor propio calculamos los vectores propios como sigue:
Para λ = −1
>> null(A + eye(3),′ r′ )
ans =
−1
1
0

−1
 
 
Por tanto el vector v1 =  1  es un vector propio de valor propio λ = −1.
 
0
Para λ = 2

>> null(A − 2 ∗ eye(3),′ r′ )
ans =
−2 −3
1
0
0
1




−3
 
 
 
 
Luego los vectores v2 =  1  y v3 =  0  son vectores propios de valor propio λ = 2.
 
 
0
1
En este caso obtenemos que E(−1) = gen{v1 } y E(2) = gen{v2 , v3 }. El subespacio propio E(−1) es un
−2
subespacio de dimensión 1 y E(2) es de dimensión 2.
193
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
El ejemplo anterior exhibe un caso en el que, para un valor propio λ, dim E(λ) es diferente de 1. En general
este espacio puede tener cualquier dimensión entre 1 y n. Los valores propios, por ser raı́ces del polinomio
caracterı́stico también tienen una multiplicidad algebraica. Como en el caso anterior la multiplidad algebraica
de λ = 2 es 2, ya que (x − 2)2 es factor de pA (x). Por tanto a un valor propio λ le podemos asociar dos enteros
positivos: la multiplicidad algebraica como raı́z del polinomio caracterı́stico y la dimensión del subespacio E(λ) .
Esto motiva la siguiente definición.
Definición 6.4. Sea A una matriz de tamaño n×n y sean λ1 , . . . λk los valores propios de A,
1. Decimos que la multiplicidad algebraica de λi , es k si (λi − x)k es la máxima potencia de λi − x que divide a
pA (λ). La multiplicidad algebraica de un valor propio λ será denotada por a(λ) .
2. La multiplicidad geométrica de λi esta dada por dim Eλi . La multiplicidad geométrica de un valor propio λ
será denotada por g(λ) .
Ejemplo 6.4. En el ejemplo anterior tenemos que a(−1) = 1 = g(2) y a(2) = 2 = g(2) .
Ejemplo 6.5. En el Ejemplo 6.2 tenemos que a(−1) = g(−1) = 1 y a(2) = g(2) = 1.

3
−1
0
0





−1
3
0
0
.
Ejemplo 6.6. (MatLab) Calcular los valores y vectores propios de la matriz A = 


 7 −1 −4
0


7 −1
0 −4
Solución. En MatLab podemos usar un comando diferente al usado en el Ejemplo 6.3 que nos permite calcular
todos los valores y vectores propios con una sola instrucción como sigue.
>> A = [3 − 1 0 0; −1 3 0 0; 7 − 1 − 4 0; 7 − 1 0 − 4]; [V, D] = eig(A)
V =
0 0
1/2
1/2
0 0
−1/2
1/2
1 0
1/2
1/2
0 1
D =
−4
1/2
1/2
0
0 0
0
−4
0 0
0
0
4 0
0
0 0 2
Con este comando los vectores propios son las columnas de la matrizV y los correpondientes
valores propios
 
0
0
 
 
 
 
0
 0

 
en la matriz D. Tenemos entonces que A tiene vectores propios v1 = 
  y v2 =   ambos de valor propio
1
 0
 
 
0
1
194

1/2


1/2









1/2
−1/2
 de valor propio λ = 2. Nótese que en este ejemplo



λ = −4, v3 = 

 de valor propio λ = 4 y v4 = 
1/2
 1/2 




1/2
1/2
se tiene que cada valor propio tiene multiplicidad geométrica y algebraica iguales. En realidad este comando nos
da mas información acerca de la matriz, ver Ejemplo 6.24.
Hasta ahora solo hemos visto ejemplos donde la multiplicidad geométrica y algebraica de cada valor propio
son iguales, pero esto no siempre se cumple. De hecho es posible que la multiplicidad geométrica sea estrictamente
menor que la multiplicidad algebraica, a continuación damos ejemplos donde se da esto.
Ejemplo
6.7. (MatLab)
Calcular los valores propios y sus multiplicidades algebraica y geométrica de la matriz


−3 −2
1




A =  1 −6
1 .


1 −2 −3
Solución. Primero calculamos el polinomio caracterı́stico del A.
>> A = [−3 − 2 1; 1 − 6 1; 1 − 2 − 3]; f actor(poly(sym(A)))
ans =
(4 + x)3
Es decir que pA (x) = (4 + x)3 y se sigue que λ = −4 es el único valor propio con multiplicidad algebraica 3.
Ahora, necesitamos el subespacio propio para calcular la multiplicidad geométrica.
>> null(A − 3 ∗ eye(3),′ r′ )
ans =
2 −1
1
0
0
1
Esto indica que E(−4)
    




2 −1


   
= gen 1 ,  0  y se sigue que g(−4) = 2 < 3 = a(−4) .

   




 0
1 
Ejemplo
6.8. (MatLab)
Calcular los valores propios y sus multiplicidades algebraica y geométrica de la matriz


−4 −1
1




A =  0 −5
1 .


−1
0 −3
Solución. Calculamos el polinomio caracterı́stico
>> A = [−4 − 1 1; 0 − 5 1; −1 0 − 3]; f actor(poly(sym(A)))
ans =
(4 + x)3
Nuevamente obtenemos que λ = −4 es el único valor propio con multiplicidad algebraica 3, ahora necesitamos
el subespacio propio para calcular la multiplicidad geométrica.
195
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
>> null(A − 3 ∗ eye(3),′ r′ )
ans =
1
1
1
Por tanto E(−4)
  



1 

  

 
= gen 1 . En este caso obtenemos que g(−4) = 1 < 3 = a(−4) .

 



 1 

Como los valores propios son las raı́ces de el polinomio caracterı́stico, y sabemos que existen polinomios con
coeficientes reales (incluso enteros) y raı́ces complejas, entonces también existen matrices con entradas reales
(enteras) y valores propios complejos. A continuación exhibimos un ejemplo.

−1


Ejemplo 6.9. (MatLab) Calcular los valores y vectores propios de la matriz A = −2

−4
Solución. Usamos MatLab para calcular los valores propios
−2 2



−1 2.

−1 3
>> A = [−1 − 2 2; −2 − 1 2; −4 − 1 3]; p = poly(sym(A))
x3 − x2 + x − 1
Depués lo factorizamos:
f actor(p)
ans =
(x − 1) ∗ (x2 + 1)
De aqui deducimos que los valores propios son λ1 = 1, λ2 = i y λ3 = −i. Ahora calculamos los vectores
propios:
>> v1 = null(c − eye(3),′ r′ )
v1 =
1/3
2/3
1
>> v2 = null(c − i ∗ eye(3),′ r′ )
v2 =
3/5 − 1/5i
3/5 − 1/5i
1
>> v2 = null(c + i ∗ eye(3),′ r′ )
v3 =
3/5 + 1/5i
3/5 + 1/5i
1
196

1/3


3/5 − 1/5i


3/5 + 1/5i













Por tanto los vectores propios son v1 = 2/3, v2 = 3/5 − 1/5i y v3 = 3/5 + 1/5i de valores propios






1
1
1
λ1 = 1, λ2 = i y λ3 = −i, respectivamente.
Problemas
6.1.1. Encuentre los valores, vectores y subespacios propios de la matriz. Determine también las multiplicidades
geométricas y algebraicas de cada valor propio.




2 −1
−2 −2
,
,
b. B = 
a. A = 
5 −2
−5
1

5 4 2





d. D = 4 5 2


2 2 2

4


g. G =  6

10
−3
−6
−9

0


1 ,

1

0
1


e. E = 0
0

1 −3

5


h. H =  7

10

c. C = 


0


1

3
−3
−7
−11
−3
1


1 ,

2

,
−3
0
−1 −2


f. F =  1

1

2



1 ,

−2 −1
−4

1
0 0


1 0
i. J = 

0 1

0 0
0 1



0 0
.

0 0

1 0
6.1.2. Sea A ∈ M3 (C) con dos valores propios distintos λ1 y λ2 . cuales son los posibles polinomios caracteristicos
de A.
Repita si A ∈ M4 (C).
6.1.3. Sean λ1 , λ2 , . . . , λk todos los diferentes valores propios de A ∈ Mn (C) con multiplicidades algebraicas
a(λ1 ) , . . . , a(λk ) , respectivamente. Demuestre que lo siguiente.
1. El vector v es un vector propio de A de valor propio λ si y sólo v es un vector propio de αA valor propio αλ.
2. Para α 6= 0, todos los diferentes valores propios de la matriz αA son αλ1 , αλ2 , . . . , αλk . Deduzca que a(λi ) es
la multiplicidad algebraica de αλi como valor propio de αA , para i = 1, . . . , k.
3. El vector v es un vector propio de A de valor propio λ si y sólo v es un vector propio de A − αI valor propio
λ − α.
4. Demuestre que todos los diferentes valores propios de A − αI son λ1 − α, λ2 − α, . . . , λk − α. Deduzca que, para
i = 1, . . . , k, la multiplicidad algebraica de λi − α como valor propio de A − αI es a(λi ) .
5. El vector v es un valor propio de A de valor propio λ si y sólo si v es un vector Am con valor propio λm .
m
m
m
6. Demuestre que λm
1 , λ2 , . . . , λk son todos los diferentes valores propios de A . Deduzca que la multiplicidad
m
algebraica de λm
es a(λi ) , para i = 1, . . . , k.
i como valor propio de A
197
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
7. Sea v es un vector propio de A con valor propio λ, f (x) = a0 + a1 x + · · · + ak xk un polinomio y f (A) la matriz
definida por f (A) = a0 I + a1 A + · · · + ak Ak , entonces v es un vector propio de f (A) con valor propio de f (λ).
Deduzca que f (λ1 ), f (λ2 ), . . . , f (λk ) son valores propios de f (A).


−2 −2
 y f (x) = 1 − 2x + 3x3 .
8. Verifique lo anterior si A = 
−5
1

6.1.4. Encuentre los valores y vectores propios de la matrices A = 
a
−a2
1
0


yB=
a
a2
1
0

.
6.1.5. Sea A una matriz simétrica 2×2 con entradas reales. Demuestre que los valores propios de A son reales.


B C
 entonces pA (x) = pB (x)pD (x).
6.1.6. Demuestre que si A = 
0 D
6.1.7. Demuestre el Lema 6.3.
6.1.8. Demuestre que si A es invertible y v es un vector propio de A entonces v es un vector propio de A−1 de
valor propio 1/λ.
6.1.9. Demuestre que si A ∈ Mn (R) y v ∈ E(λ) entonces v̄ ∈ E(λ̄) .
6.1.10. Demuestre que A es invertible si y sólo si λ = 0 no es un valor propio de A si y sólo si pA (0) 6= 0.
6.1.11. Si P es una matriz proyección, es decir, si P 2 = P y P 6= I entonces det P = 0. (Recuerde que P visto
como aplicación lineal satisface que ImP = ColP = {v | P v = v} y KerP = (ImP )⊥ )
6.1.12. Demuestre que si A es nilpotente, es decir, si Ak = 0 para algún k > 0, entonces λ = 0 es el único
valor propio de A.
6.1.13. Demuestre que si A2 = I entonces los valores propios de A son λ = 1 o λ = −1.
6.1.14. Si λ1 , . . . , λk son todos los valores propios de A entonces
1
1
λ1 , . . . , λk
son todos los valores propios de
A−1 .
6.1.15. Si λ1 , . . . , λn son los valores propios de A entonces det(A) = λ1 · · · λn .
6.1.16. Demuestre que A + I es invertible si y sólo si λ = −1 no es un valor propio de A.
6.1.17. Si A ∈ Mn (C) es invertible, demuestre que existe α ∈ Cn tal que A + αI no es invertible.
6.1.18. Sea A ∈ Mn (C), demuestre que A y At tienen el mismo polinomio caracterı́stico, es decir, pA (x) =
pAt (x). Deduzca que A y At tienen los mismos valores propios.
 0 0 0 ··· 0 −a0 
1 0 0 ··· 0
 0 1 0 ··· 0
6.1.19. Si A = 
 ... ... ... . . . ...
−a1
−a2
..
.
0 0 0 ··· 0 −an−2
0 0 0 ··· 1 −an−1

 demuestre que pA (x) = (−1)n (xn + an−1 xn−1 + · · · + a1 x + a0 ).

Exhiba una matriz A cuyo polinomio caracterı́stico sea pA (x) = x4 − x + 1.
198
6.2.
Matrices Similares
En esta sección se definen los conceptos de matrices similares y matriz diagonalizable. Veremos que no todas
las matrices son diagonalizables, que matrices similares tienen el mismo polinomio caracterı́stico y usaremos esto
para mostrar que la multiplicidad geométrica de un valor propio es menor o igual a su multiplicidad algebraica.
Definición 6.5. Sean A y B matrices de tamaño n×n, decimos que A y B son similares si existe una matriz
invertible C tal que A = CBC −1 . Escribiremos A ∼ B para denotar que A y B son similares.






1 −1
3 0
2 1
, se
 son similares. Ya que si se toma C = 
yB=
Ejemplo 6.10. Las matrices A = 
1
1
0 1
1 2
tiene que A = CBC −1 .
La siguiente propiedad de matrices similares es importante para lo que sigue.
Teorema 6.5. Matrices similares tienen el mismo polinomio caracterı́stico. Es decir, si A, BMn (C) son similares entonces pA (x) = pB (x). Se deduce además que matrices similares tienen los mismos valores propios.
Demostración. Como A y B son similares, existe una matriz invertible C tal que B = CAC −1 , luego
pB (λ) = det(B − λI) = det(CAC −1 − λI) = det(CAC −1 − λCIC −1 )
= det C(A − λI)C −1 = det(C) det(A − λI) det(C −1 )
= det(C) det(A − λI)
1
= det(A − λI)
det(C)
= pA (λ).
Hay un caso especial de similaridad de matrices que definimos a continuación y será tratado más a fondo
en la Sección 6.4.
Definición 6.6. Sea A una matriz de tamaño n×n, decimos que A es diagonalizable si existe una matriz
diagonal D tal que A ∼ D.

Ejemplo 6.11. La matriz A = 

la matriz diagonal 
3
0

0
.
1
2
1

1
 es diagonalizable ya que en el Ejemplo 6.10 vimos que A es similar a
2
Es importante aclarar que no todas las matrices son diagonalizables. A continuación exhibimos un ejemplo.


1 1
 no es diagonalizable. Por el absurdo supongamos que existe
Ejemplo 6.12. Veamos que la matriz A = 
0 1


a 0
.
una matriz D diagonal tal que A ∼ D, con D = 
0 b
199
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Nótese que los valores propios de A son λ = 1 con multiplicidad 2 y los valores propios de D son λ = a y
λ = b. Como A ∼ D, entonces por el Teorema 6.5 A y D tienen los mismos valores valores propios, por tanto
a = b = 1, entonces D = I.
Finalmente, como A ∼ D(= I), existe una matriz invertible C tal que A = CDC −1 por tanto


1 1
0 1


 = A = C D C −1 = CIC −1 = I = 
|{z}
=I
1
0

0

1
De esta igualdad se sigue que 1 = 0, lo que es absurdo. Concluimos que A no es diagonalizable.
Este
también muestra que el recı́proco del Teorema 6.5 no es cierto. De acuerdo al ejemplo, la matriz

 ejemplo
1 1
 y la matriz identidad tienen los mismos valores propios y en consecuencia el mismo polinomio
A = 
0 1
caracterı́stico, sin embargo no son similares.
La pregunta natural es bajo cuales condiciones una matriz es diagonalizable. La respuesta está en la Sección
6.4, más precisamente los Teoremas 6.13 y 6.15, caracterizan las matrices diagonalizables.
En los ejemplos de la sección anterior vimos que la multiplicidad geométrica de de los valores propios es
menor o igual a la multiplicidad algebraica, esto es cierto en general.
Teorema 6.6. Sea A una matriz de tamaño n×n y sea λ un valor propio de A, entonces g(λ) ≤ a(λ) , es decir,
multiplicidad geométrica de λ ≤ multiplicidad algebraica de λ.
Demostración. Sea λ un valor propio de A, Como λ es un valor propio, entonces existe v 6= 0 tal que Av = λv
y por tanto E(λ) 6= 0.
Sea k = dim E(λ) , es decir k = g(λ) , y sean {v1 , . . . , vk } es una base para E(λ) . Tenemos entonces que
Avi = λvi para i = 1, . . . , k. Ahora tomemos wk+1 , . . . , wn tal que {v1 , . . . , vk , wk+1 , . . . , wn } es una base para
h
i
Cn y sea S = v1 . . . vk wk+1 . . . wn . Como {v1 , . . . , vk , wk+1 , . . . , wn } es una base, entonces por el
Corolario 2.13 tenemos que S es invertible y se tiene que
h
I = S −1 S = S −1 v1 · · ·
h
= S −1 v1 · · ·
vk
wk+1
S −1 vk
···
S −1 wk+1
wn
i
···
i
S −1 wn ,
de donde se sigue que S −1 v1 = e1 , . . . , S −1 vk = ek .
Ahora definamos B = S −1 AS, de esto se sigue que A y B son similares y por el teorema anterior tenemos
200
que pA (x) = pB (x) y la matriz B tiene la siguiente forma:
h
i
B = S −1 AS = S −1 A v1 · · · vk wk+1 · · · wn
#
"
Av
Aw
·
·
·
Aw
·
·
·
Av
1
k+1
n
k
= S −1 |{z}
|{z}
λv1
λvk
h
= S −1 λv1 · · ·
"
S −1 λv · · ·
= | {z }1
λvk
−1
= λ |S {z v} · · ·
h
···
λ S −1 vk S −1 Awk+1
| {z }
ek
λek
S −1 Awk+1

λ
.
.
.


0
=

0

.
 ..

0
h
donde R = S −1 Awk+1
···
Awn
i
···
S −1 Awn
···
S −1 Awn
λS −1 vk
e1
= λe1
···
S −1 λvk S −1 Awk+1
| {z }
λS −1 v1
"
Awk+1
···
..
.
0
..
.
···
λ
···
..
.
0
..
.
···
0
S −1 Awn
···







R






i

S −1 Awn . Si escribimos R = 
una matriz (n − k) × (n − k), tenemos que


λ ··· 0
.

.
 . ..

. .. R1 
.




0 · · · λ



B=
y por tanto

0 · · · 0



. .

. . ... R2 
 ..


0 ··· 0
R1
R2

#
#
i

 con R1 una matriz k × (n − k) y R2 es
λ−x
 .
 .
 .


 0
B − xIn = 

 0

 .
 ..

0
···
..
.
0
..
.
···
λ−x
···
..
.
0
..
.
···
0







.




R2 − xIk 

R1
Se sigue del Teorema 5.7 que pB (x) = det(B − xI) = (−1)k (λ − x)k × det(R2 − xIk ). En consecuencia, como A
y B son similares, tenemos que
pA (x) = pB (x) = det(B − xI) = (−1)k (λ − x)k × det(R2 − xIk ).
Se sigue que (λ − x)k es un factor de pA (x) y por tanto la multiplicidad algebraica de λ como raı́z de pA (x) es
mayor o igual a k, es decir, k ≤ a(λ) . Concluimos que
g(λ) = k ≤ a(λ) .
201
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Problemas
6.2.1. Determine cual de las siguientes 3 matrices es diagonalizable





3 0 0
3 1 0
3 1










a. A = 0 3 0
b. B = 0 3 0
c. C = 0 3





0 0 3
0 0 3
0 0



3
0




0 y C=0


0
3
3 1


6.2.2. Muestre que las matrices B = 0 3

0 0
1 0


0


1

3


3 1no son similares.

0 3
6.2.3. Sea v ∈ Cn \ {0} y P = vv t , demuestre que v es un vector propio de P y que E0 = V ⊥ con V = gen{v}.


2b −b2
 no es diagonalizable, para ningún b ∈ C. Muestre que la matriz
6.2.4. Muestre que la matriz A = 
1
0


2
−2b −b
 tampoco es diagonalizable para ningún b.
B=
1
0

6.2.5. Muestre que la matriz A = 
λ
1
0
λ

6.2.6. Muestre que las matrices A = 

 no es diagonalizable, para ningún λ ∈ C.
λ1
0
0
λ2


yB=
λ1
1
0
λ2

 son similares si y sólo si λ1 6= λ2 .
6.2.7. Demuestre que si B es invertible entonces AB y BA son similares.


0 a b




6.2.8. Demuestre que la matriz A = 0 0 c  es diagonalizable si y sólo si a = b = c = 0.


0 0 0

a


6.2.9. Demuestre que las matrices A = 0

0
b
a
0
c


a




d y B =  0


0
a
0
a
0

0


0 son similares si y sólo si a = b = c = 0.

0
MOVER PROBLEMAS DEL FINAL HACIA ESTA SECCIÓN Y AGREGAR OTROS
6.3.
Cambio de Base
El objetivo de esta sección es demostrar que dos matrices son similares si y sólo si están relacionadas por
un cambio de coordenadas (cambio de base), para llegar a esto debemos definir cambio de coordenadas.
202
Definición 6.7. Sean X = {v1 , . . . , vn } una base de Rn y v ∈ Rn , sabemos que existen escalares α1 , . . . , αn
talque v = α1 v1 + · · · + αn vn y que esta representación
es única. Definimos la representación del vector v en
 
α1
 
 .. 
términos de la base X como el vector vX =  .  .
 
αn

 
 
 

−1 
1
4
Ejemplo 6.13. Sea X = v1 =   , v2 =   . Nótese que si w =   tenemos que v = 3v1 − v2 y por


2
1
1
 
3
tanto wX =  .
−1
En la siguiente figura se pueden observar los vectores de la base X del ejemplo anterior y el vector w.
3
2
v2
1
b
e2
−4
−3
−2
−1
v1
e1
1
w
2
3
4
−1
−2
−3
−4
 
4
Cuando escribimos que w =   estamos en realidad dando la posición del vector w con respecto a los vectores
1
e1 y e2 , ya que w = 4e1 + e2 . Es decir, las componentes de w no son más que las coordenadas del vector con
respecto a los vectores de la base estándar. El vector wX en cambio, nos está dando las coordenadas del vector
w con respecto a la base X, ya que w = 3v1 − v2 (como se puede verificar en la gráfica).
Esto nos permite decir que las componentes del vector vX son las coordenadas del vector v con respecto a los
vectores v1 y v2 de la base X.
A continuación definimos la matriz de cambio de base, que nos permitirá cambiar las coordenadas de un
vector de una base a otra.
Definición 6.8. Sean X = {v1 , . . . , vn } y Y = {w1 , . . . , wn } bases para Rn , definimos la matriz del cambio de
base (o cambio de coordenadas) de la base X a la base Y como la matriz.
Y IX
h
= (v1 )Y
···
i
(vn )Y .
 
 
0 
1
Ejemplo 6.14. Sean E y X las bases de R2 definidas por E = e1 =   , e2 =   la base estándar y

1 
0


203
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
 
 
−1 
1
X = v1 =   , v2 =   , de la definición anterior se tenemos que la matriz

2 
1


h
E IX
= (v1 )E
i
h

i
(v2 )E = v1
v2 = 
1 −1
1
2
E IX
está dada por

.
En el siguiente teorema establecemos la propiedad que caracteriza la matriz de cambio de base.
Teorema 6.7. Sean X = {v1 , . . . , vn } y Y = {w1 , . . . , wn } bases para Rn y sea v ∈ Rn , entonces
vY = Y IX · vX .
Más aún, la matriz de cambio de base es la única con esta propiedad.
Demostración. Como X es una base, existen constantes β1 , . . . , βn tal que
v = β1 v 1 + · · · + βn v n
(6.8)

β1
 
 . 
de la definición tenemos que vX =  ..  , y como Y es una base, para 1 ≤ i ≤ n, existen constantes α1i , . . . , αni
 
βn
tal que


vi = α1i w1 + · · · + αni wn ,

α1i
 
 . 
luego (vi )Y =  .. , por tanto
 
αni
Y IX
h
= (v1 )Y
···

α11
i 
 ..
(vn )Y =  .

αn1
(6.9)
···
..
.
···

α1n

.. 
. 

αnn
De las Ecuaciones (6.8) y (6.9) tenemos que
v = β1 v 1 + · · · + βn v n
= β1 (α11 v1 + · · · + αn1 vn ) + · · · + βn (α1n v1 + · · · + αnn vn )
= (β1 α11 + · · · + βn α1n )v1 + · · · + (β1 αn1 + · · · + βn αnn )vn
luego

 
β1 α11 + · · · + βn α1n
α11

 
..

  ..
vY = 
= .
.

 
β1 αn1 + · · · + βn αnn
αn1
|
···
..
.
···
{z
Y
IX
 
α1n
β1
 
..   .. 
  = Y IX vY .
. 
 . 
αnn
βn
} | {z }
vY
204
Para la segunda parte, supongamos que A es tal que vY = AvX para todo v ∈ Rn . En particular se tiene que
para i = 1, . . . , n se tiene que (vi )Y = A(vi )X . Como (vi )X = ei se sigue que
(vi )Y = A(vi )X = Aei = iésima columna de A.
Se sigue por tanto que las columnas de A son los vectores (v1 )Y , . . . , (vn )Y , es decir, A = [ (v1 )Y · · · (vn )Y ].
Cada base determina ejes coordenados de Rn . Éstos ejes corresponden a las lı́neas generadas por cada uno de
los vectores de la base. El Teorema anterior muestra que la matriz de cambio de base
Y IX
sirve para determinar
las coordenadas en términos de la base Y de un vector escrito en términos de una base X. Esto se ilustra en el
siguiente ejemplo.
 
 
−1 
1
Ejemplo 6.15. Sean E = {e1 , e2 } la base estándar de Rn y X = v1 =   , v2 =   . Sea v = 3v1 − v2 ,

2 
1


 
1 −1
3
, entonces
se sigue que vX =  . Por el Ejemplo 6.14 se tiene que E IX = 
1
2
−1



v = vE = E IX vX = 
 
4
  =  .
1
−1
2
1 −1
1

3

Como se muestra en la siguiente figura, estas dos bases determinan dos sistemas de ejes para R2 , uno
determinado por los vectores de la base X y otro determinado por los vectores de la base estándar y la matriz
E IX
permite cambiar las coordenadas de un vector, en términos de la base X, a las coordenadas en términos
de la base estándar. Usando la figura también se pueden determinar las coordenadas del vector w con respecto
a cada una de estas bases.
6
4
v2
e2 v 1
v2
w
2
e2
v1
w
b
e1
b
−4
e1
−2
−2
−4
2
4
6
205
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

 
 
 



4 
3
2
−1
Ejemplo 6.16. Considere las bases X = v1 =   , v2 =   y Y = w1 =   , w2 =   de R2 y


1 
1
1 
0
v = 2v1 + 3v2 , expresar a v en términos de la base Y .
 
 
2
1
Solución. Nótese que v1 = w1 − w2 y v2 = 2w1 − w2 , luego (v1 )Y =   y (v2 )Y =  , de donde
−1
−1
 


2
1
2
. Ahora, como vX =  , entonces

Y IX =
3
−1 −1
   

8
2
1
2
  =  .
vY = Y IX vX = 
−5
3
−1 −1



Es decir, v = 8w1 − 5w2 .
El siguiente teorema describe una forma de calcular la matriz de cambio de base.
h
Teorema 6.8. Sean X = {v1 , . . . , vn } y Y = {w1 , . . . , wn } bases para Rn y sean A = v1
h
i
w1 · · · wn . Entonces Y IX = B −1 A.
···
i
vn y B =
Demostración. Expresando los vectores v1 , . . . , vn en términos de la base Y obtenemos:
v1 = α11 w1 · · · + αn1 wn
..
.
.
(6.10)
vn = α1n w1 · · · + αnn wn



α11
α1n




 . 
 . 
Entonces (v1 )Y =  ..  , . . . , (vn )Y =  ..  y por tanto




αn1
αnn
De la Ecuación (6.10) tenemos que

h
v1
|
por tanto A = B
Y IX ,
···
{z
=A
i h
v n = w1
} |
···
{z
=B
Y IX

α11

 ..
= .

αn1

α11
i
 ..
wn  .
}
αn1
|
···
···
..
.
···
{z
=Y IX
multiplicando a ambos lados por B −1 obtenemos
Y IX
···
..
.

α1n

.. 
.
. 

αnn

α1n

.. 
,
. 

αnn
}
= B −1 A.
De este teorema se sigue un procedimiento para calcular la matriz del cambio de base, el cual damos a continuación.
Procedimiento 6.2. (Procedimiento para calcular la matriz del cambio de base) Sean X = {v1 , . . . , vn }
h
i
h
i
y Y = {w1 , . . . , wn } bases para Rn y sean A = v1 · · · vn y B = w1 · · · wn entonces
206
h
i
1. Aplicar reducción Gauss-Jordan a la matriz aumentada B A hasta encontrar su forma escalonda reducida.
"
#
−1
2. Al final del paso 1. obtenemos I B
| {z A} . Luego en la parte derecha de la matriz aumentada se obtiene la
Y
matriz de cambio de base
IX
Y IX .

 
 
 
 

1 
2
1 
1
Ejemplo 6.17. Considere las bases X = v1 =   , v2 =   y Y = w1 =   , w2 =   de R2 ,


0 
−1
−1 
1
 
1
calcular Y IX y vY si vX =  .
1


h
i
2 1 1
1
 obtenemos la matriz
Al reducir la matriz w1 w2 v1 v2 = 
−1 0 1 −1




1 0 −1
1
−1
1


 y por tanto Y IX = 
0 1
3 −1
3 −1
 
0
Por el Teorema 6.7 tenemos que vY =Y IX · vX =  .
2


 
 
 

1 
1
2

 
 
 
 
 
 
3
Ejemplo 6.18. (MatLab) Sean X y Y las bases de R definidas por X = v1 = 1 , v2 =  2  , v3 = −2

 
 
 





3 
−2
1

 
 
 



1 
1
1

 
 
 


 
 
 
y Y = w1 = 2 , w2 = 1 , w3 = 1 . Calcular la matriz de cambio de base Y IX y calcular vY si v =

 
 
 





1 
2
3
2v1 − v2 + v3 .





Solución. Por el procedimiento anterior la matriz de cambio de base es simplemente el producto de las matrices
h
i
h
i
B −1 y A donde A = v1 v2 v3 y B = w1 w2 w3 . En MatLab hacemos lo siguiente:
>> A = [2 1 1; 1 2 − 2; 1 − 2 3]; B = [1 1 1; 2 1 1; 3 2 1]; yIx = inv(B) ∗ A
yIx =
−1
1
−3
1
−5
8
2
5
−4
Se sigue que la matriz de cambio de base está dada por


Y IX

−1


= 1

2
1
−5
5
−3



8 . Ahora, para el calculo de

−4
2
 
 
vY , tenemos que vX = −1 y vY =Y IX vX , esto lo hacemos en MatLab como sigue:
 
1
>> vx = [2; −1; 1]; vy = yIx ∗ vx
vy =
207
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
−6
15
−5
Obtenemos que v = −6w1 + 15w2 − 5w3 .
Las matrices de cambio de base cumplen las siguientes propiedades.
Teorema 6.9. Sean X = {v1 , . . . , vn }, Y = {w1 , . . . , wn } y Z = {u1 , . . . , un } bases de Rn entonces se cumple
que:
1.
Y IX
= (X IY )−1
2.
Z IX
= Z I Y ·Y I X
h
Demostración. 1. Sean A = v1
B
−1
Ay
X IY
−1
=A
B, por tanto
i
h
v n , B = w1
···
(X I Y )
2. Sea C =
Z IX
h
u1
···
un
= C −1 A, entonces
i
−1
= A−1 B
i
wn , por el Teorema 6.8 tenemos que
···
−1
=
= B −1 A =Y IX .
entonces por el Teorema 6.8 tenemos que
Z IX
Y IX
Y IX
= B −1 A,
Z IY
= C −1 B y
= C −1 A = C −1 BB −1 A =Z IY ·Y IX .
 
 
−1 
1
Ejemplo 6.19. Sean E la base estándar de Rn y X = v1 =   , v2 =   . En el Ejemplo 6.14 obtuvimos

2 
1


1 −1
 . Por el Teorema anterior anterior tenemos
que la matriz de cambio de base E IX está dado por E IX = 
1
2
que la matriz de cambio de base X IE está dada por




X IE = ( E IX )
−1
=
2
3
− 13
1
3
1
3
.


2
−1 
2
Ahora, sea Y = w1 =   , w2 =   . Se sigue que E IY = [ (w1 )E (w2 )E ] = [ w1 w2 ] = 


−1
−1
−1
Por el teorema anterior obtenemos que

 
 

1
2
1
−1
2
−1
.
=
 3 3 
X IY = X IE · E IY =
−1
0
−1 −1
− 13 31






−1
.
−1
Se deja de ejercicio al lector verificar este cálculo usando el Procedimiento 6.2.
6.3.1.
La matriz de una transformacion con respecto a dos bases
La siguiente generalización de la definición de matriz de una transformación. La definición anterior depende
de las bases estándar y aca se hace para cualquier base del dominio y cualquier base del codominio.
208
Definición 6.9. Sea T : Rn −→ Rm una transformación lineal y sean X = {v1 , . . . , vn } y Y = {w1 , . . . , wm }
bases para Rn y Rm , respectivamente. Definimos la matriz de T con respecto a las bases X y Y , denotada por
Y
TX como la matriz
Y
h
TX = T (v1 )Y
···
i
T (vn )Y .
La matriz de una transformación es la matriz con respecto a las bases estándar.
Observación 6.2. Si T : Rn −→ Rm es una transformación lineal y E = e1 , . . . , en y E = e1 , . . . , em son las
bases estándar de Rn y Rm , respectivamente, y S es la matriz de T , es decir, la matriz tal que T (x) = Sx, para
todo x ∈ Rn , entonces
S=
E TE
h
= T (e1 )
...
i
T (en ) .
2
2
Ejemplo
6.20.
la transformación

definida por T (x, y) = (2x + 2y, 2y) y sean
lineal
 
  Sea T : R−→ R 



0 
2
1
1
X = v1 =   , v2 =   y Y = w1 =   , w2 =   bases de R2 . Determine la matriz Y TX de T


−1 
1
−1 
1
con respecto a la bases X y Y .
Solución. Nótese que T (v1 ) = (4, 2) = 2w1 y T (v2 ) = (0, −2) = 2w2 ,

2

Y TX = [ T (v1 )Y T (v2 )Y ] =
0
La importancia de la matriz de la transformación
Y
vector en términos de X, vX , el producto de la matriz
se sigue entonces que

0
.
2
TX es el hecho que si tenemos las coordenadas de un
Y
TX por vX nos da las coordenadas de la imagen de
v, T (v), en términos de la base Y . Al igual que la matriz de cambio de base, esta matriz está determinada de
manera única por dicha propiedad.
Teorema 6.10. Sea T : Rn −→ Rm una transformación lineal, sean X = {v1 , . . . , vn } y Y = {w1 , . . . , wm }
bases para Rn y Rm , respectivamente, y sea v ∈ Rn . Entonces
T (v)Y =
Y
TX v X .
Además tenemos que si existe una matriz A tal que V vX = T (v)Y para todo v ∈ Rn , entonces A = Y TX .
Demostración. Como X es una base, existen constantes β1 , . . . , βn tal que
v = β1 v 1 + · · · + βn v n
y se tiene que vX
que
(6.11)

β1
 
 . 
=  ..  . Como Y también es una base, para 1 ≤ i ≤ m, existen constantes α1i , . . . , αmi tal
 
βn

T (vi ) = α1i w1 + · · · + αmi wm ,
(6.12)
209
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO


α1i


 . 
luego T (vi )Y =  ..  y por tanto


αmi
Y
h
TX = T (v1 )Y
···
De las Ecuaciones (6.11) y (6.12) tenemos que

α11
i 
 .
T (vn )Y =  ..

αm1
···
..
.
···

α1n

.. 
. 

αmn
T (v) = β1 T (v1 ) + · · · + βn T (vn )
= β1 (α11 w1 + · · · + αm1 wn ) + · · · + βn (α1n w1 + · · · + αmn wn )
= (β1 α11 + · · · + βn α1n )w1 + · · · + (β1 αm1 + · · · + βn αmn )wn
Se sigue que
 
α11
β1 α11 + · · · + βn α1n
 

..
  ..

T (v)Y = 
= .
.
 

αm1
β1 αn1 + · · · + βn αnn
|

n
···
..
.
···
{z
Y
TX
 
α1n
β1
 
..   .. 
  = Y TX v X .
. 
 . 
αmn
βn
} | {z }
vX
Si A satisface que AvX = T (v)Y para todo v ∈ R , entonces para i = 1, . . . , n tenemos que T (vi )Y = A(vi )X =
Aei = i-ésima columna de A. Se sigue que las columnas de A son T (v1 )Y , . . . , T (vn )Y y por tanto
A = [ T (v1 )Y · · · T (vn )Y ] = Y TX .
En el siguiente teorema se hace explı́cito un procedimiento para calcular la matriz
Y
TX .
Teorema 6.11. Sea T : Rn −→ Rm una transformación lineal, sean X = {v1 , . . . , vn } y Y = {w1 , . . . , wm }
h
i
h
i
bases para Rn y Rm , respectivamente y sean A = v1 . . . vn y B = w1 . . . wm , entonces
h
i
−1
T
=
B
T (v1 ) · · · T (vn ) ,
Y X
más aún
Y
TX = B −1 ·E TE · A.
Demostración. La demostración se hace de manera directa como sigue
i h
i
h
· · · T (vn )Y = Y IE T (v1 )E · · · Y IE T (vn )E
X TY = T (v1 )Y
h
i
i
h
= Y IE T (v1 ) · · · Y IE T (vn ) = Y IE T (v1 ) · · · T (vn )
h
i
h
i
= B −1 E TE v1 · · · E TE vn = B −1 E TE v1 · · · vn
= B −1 E TE A
210
A continuación damos un procedimiento para calcular la matriz de una transformación T : Rn −→ Rm con
respecto a dos bases X = {v1 , . . . , vn } y Y = {w1 , . . . , wm }, basado en el teorema anterior
Procedimiento 6.3. (Procedimiento para calcular
Y TX )
Con Las mismas hipótesis del teorema anterior,
h
1. Se calcula T (vi ) para i = 1, . . . , n,
2. Se aplica reducción Gauss-Jordan a la matriz aumentada
h
w1
···
wn
|
T (v1 )
···
T (vn )
i
=
=
h
h
B
T (v1 )
B
E TE
·A
···
i
i
T (vn )
hasta llevarla a la forma escalonada reducida.
3. Al final del paso 2., considerando que B es invertible, obtenemos
"
B
|
I
−1
·E T E · A
{z
}
Y
TX
#
.
Por tanto las últimas n columnas de la matriz en forma escalonada reducida del paso 3. son las columnas de la
matriz
Y
TX .


 
2x
−
y
x
, sean X =
Ejemplo 6.21. Sea T : R2 −→ R2 la transformación lineal definida por T   = 
x+y
y


 
 
 
 


1 
2
1 
1
v1 =   , v2 =   y Y = w1 =   , w2 =   bases de R2 . Calcule la matriz Y TX y T (v)Y si


0 
−1
−1 
1
 
1
vX =  
1


2 −1
 y ası́
Solución. Primero nótese que E TE = 
1
1

T (v1 ) =E TE · v1 = 
    
1
1
· = 
2
1
1
2 −1
1
h
Se necesita reducir la matriz w1

forma escalonada es la matriz 
w2
1 0
0 1
|
T (v1 )
−2 0
5
3

y
T (v2 ) =E TE · v2 = 
i

T (v2 ) = 
2
1
|
1
−1 0
|
2

TX = 

T (v)Y =Y TX · vX = 
−2 0
5
−2
5
3
 
3
 ·   =  .
0
−1
1
2 −1
1
 
1


3
 y fácilmente se verı́fica que su
0
 . Se sigue por que
Y
Finalmente, tenemos que:


.
    
−2
1
0
 ·   =  .
8
1
3
211
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO


  
x + y + 3z


x


  


2x
+
y
−
2z
  
3
4
 y

Ejemplo 6.22. (MatLab) Sea T : R −→ R la tranformación definida por T y  = 

  
 x + 2y + z 


z
−x − y + 2z

 
 
 
 


 
 
 


1
1
1
1 

 
 

 

 





1
1
2
 

 
 

 




 
 
 









2
1
1
1
 
 
 
 , w2 =   , w3 =   , w4 =   bases
sean X = v1 = 1 , v2 =  2  , v3 = −2 y Y = w1 = 
 
 
 
 


 
 
 

3
2

 1
 1 














 


3
−2
1



4
3
2
1 
de R3 y R4 , respectivamente. Calcule la matriz
Y
TX y T (v)Y si v = x1 − x2 + x3 .
Solución. Usamos el Teorema 6.11 que nos dice que Y TX = B−1 ·E TE · A,con



1
1 1 1 1



2
1
1





 2
2 1 1 1


 y E TE = 
A = [v1 v2 v3 ] = 1
2 −2, B = [w1 w2 w3 w4 ] = 





 1
3 2 1 1



1 −2
3
−1
4 3 2 1
En MatLab solo necesitamos multiplicar las matrices, lo cual hacemos a continuación.
1
3



−2
.

2
1

−1
2
1
>> A = [2 1 1; 1 2 − 2; 1 − 2 3]; B = [1 1 1 1; 2 1 1 1; 3 2 1 1; 4 3 2 1];
eT e = [1 1 3; 2 1 − 2; 1 2 1; −1 − 1 2]; yT x = inv(B) ∗ eT e ∗ A
yT x =
−3
11
−14
5
−16
20
−8
−5
1
12
7
1

−3
11
−14





 5 −16
20 
 . Finalmente, para calcular T (v) multiplicamos
Entonces Y TX = 
Y


 −8 −5
1


12
7
1
>> vx = [1; −1; 1]; T vy = yT x ∗ vx
Y

1

 
 
TX por vX = −1.
 
1
T vy =
−28
41
−2
6

−28





 41 

 . Lo que equivale a decir que T (v) = −28w1 + 41w2 − 2w3 + 6w4 .
Por tanto T (v)Y = 

 −2 


6
En MatLab también se puede usar el Procedimiento 6.3 para calcular la matriz Y TX de la siguiente forma.
212
Primero nótese que
[T (v1 )
T (v3 )] = [E TE v1
T (v2 )
E TE v 2
E TE v 3 ]
= E T E [v 1
v2
v3 ] =E TE A.
Después se calcula la matriz escalonada reducida de la matriz [B | E TE A]. En MatLab lo calculamos como sigue:
>> C = [B, eT e ∗ A]; rref (C)
ans =
1 0
0 0
−3
11
−14
0 1
0 0
5
−16
20
0 0
1 0
−8
−5
1
0 0 0 1 12
7
1
Nótese que en la respuesta se tiene la matriz identidad en la parte izquierda y las tres últimas columnas
coinciden con las columnas de la matriz
Y
TX calculada arriba.
Concluimos la sección mostrando que las matrices de tranformaciones de Rn con respecto a bases distintas
son similares. Se muestra en realidad que dos matrices son similares si y sólo si las transformaciones lineales
definidas por estas matrices están relacionados por un cambio de base.
Corolario 6.12. Sea T : Rn −→ Rn una transformación lineal y sea X = {v1 , . . . , vn } una base para Rn .
Entonces las matrices
X TX
y
E TE
son similares. Más aún si A, B ∈ Mn (R) son matrices similares y tomamos
la transformación T : Rn −→ Rn definida por T (v) = Av, entonces existe una base X de Rn tal que B = X TX .
Es decir, A y B son la matriz de la misma transformación con respecto a bases diferentes.
h
i
Demostración. Sea A = v1 · · · vn . Por el Teorema 6.11 tenemos que X TX = A−1 ·E TE · A, o equivalentemente
E TE
es decir
E TE
y
X TX
= A · X TX · A−1 ,
son similares.
Para la segunda parte, supongamos que A ∼ B y sea T : Rn −→ Rn definida por T (v) = Av. Es fácil ver
que
E TE
= A, ya que por la definición de T se tiene que T (ei ) = Aei = iésima columna de A. Pero T (ei ) es
también la iésima columna de
E TE .
Como A y B son similares, existe una matriz invertible C tal que A = CBC −1 , o equivalentemente B =
C −1 AC. Sean v1 , . . . , vn las columnas de C, como C es invertible, tenemos que X = {v1 , . . . , vn } es LI y por
tanto una base para Rn .
Por el Teorema 6.11 tenemos que
X TX
= C −1 E TE C = C −1 AC = B. Concluimos que A = E TE y B = X TX
son ambas matrices de T con respecto a diferentes bases.
Problemas
6.3.1. Determine
E TE
si T (2, 1) = (3, 1) y T (1, 1) = (1, 2).
213
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
6.3.2. Demuestre que si A y B son similares entonces det A = det B y traza(A) = traza(B). En el segundo
caso use el hecho que traza(AB) = traza(BA).
6.3.3. Sea T : Rn −→ Rn una transformación lineal y sean X y Y son bases de Rn , demuestre lo siguiente:
1. det X TX = det Y TY .
2. traza(X TX ) = traza(Y TY ).
6.3.4. Sean T, S : Rn −→ Rn transformaciones lineales y X una base de Rn . Demuestre que
X TX
+ X SX , y
X (λT )X
=λ
X TX
X (T
+ S)X =
donde T + S, λT : Rn −→ Rn son las transformaciones lineales definidas por
(T + S)(v) = T (v) + S(v) y (λT )(v) = λT (v).
6.3.5. Sea I : Rn −→ Rn la transformación identidad, es decir, la transformación definida por I(v) = v.
Demuestre que
X IX
= In , donde In es la matriz identidad de tamaõ n × n.
6.3.6. Sea T : Rn −→ Rn y supongamos que existe v ∈ R tal que {v, T (v), . . . , T n−1 (v)} es una base de Rn y
 0 0 0 ··· 0 −a0 
1 0 0 ··· 0
 0 1 0 ··· 0
T n (v) = −a0 v − a1 T (v) − · · · − an−1 T n−1 (v). Muestre que T = 
 ... ... ... . . . ...
−a1
−a2
..
.
0 0 0 ··· 0 −an−2
0 0 0 ··· 1 −an−1



6.3.7. Sea T : V −→ V una transformación lineal y X una base de V , demuestre que T : V −→ V es invertible
si y sólo si la matriz
6.4.
X TX
es invertible, para toda base X de Rn .
Diagonalización
En esta sección se darán condiciones equivalentes a que una matriz sea diagonalizable, comenzamos con el
siguiente resultado.
Teorema 6.13. Sea A una matriz de tamaño n×n, entonces A es diagonalizable si y sólo si

 A tiene n vectores
λ1 0 · · · 0




 0 λ2 . . . 0 


propios linealmente independientes. En este caso A es similar a la matriz diagonal D =  .
.. . .
.. 

 ..
.
.
.


0
0 · · · λn
donde λ1 , . . . , λn son los valores propios de A y si los correspondientes vectores propios son v1 , . . . , vn entonces
h
i
A = CDC −1 con C = v1 · · · vn .
Demostración. “ ⇒ ” Supongamos que A es diagonalizable, entonces existe una matriz D diagonal y una
matriz invertible C tal que A = CDC −1 . Sean c1 , . . . , cn las columnas de C y λ1 , . . . , λn las entradas en la
diagonal de D.
Afirmación: Los vectores c1 , . . . , cn son vectores propios de A con valores propios λ1 , . . . , λn .
214
Como A = CDC −1 entonces AC = DC, por tanto
[Ac1
Acn ] = A[c1 · · · cn ] = AC = DC


λ1 · · · 0


.. 
.
..
=  ..
 [c 1 · · · c n ] = [λ 1 c 1
.
.


0 · · · λn
···
λn cn ].
···
De esta igualdad se sigue que Ac1 = λ1 c1 , · · · , Acn = λn cn , lo que demuestra la afirmación.
Finalmente, como la matriz C es invertible, entonces sus columnas c1 , . . . , cn son linealmente independientes,
por tanto A tiene n vectores propios linealmente independientes.
“ ⇐ ” Sean v1 , . . . , vn vectores propios linealmente independientes de A con valores propios λ1 , . . . , λn , respectivamente, es decir, Avi = λi vi , para i = 1, . . . , n.
Sea X = {v1 , . . . , vn } entonces X es una base para Rn y sea T : Rn 7−→ Rn la transformación lineal determinada
por A, es decir, T (x) = Ax, para todo x ∈ Rn .
h
Como T (ei ) = Aei = i-ésima columna de A, entonces E TE = A. Ahora, sea C = v1
Teorema 6.11 tenemos que
X TX
···
= C −1 E TE C = C −1 AC, por tanto
|{z}
i
vn , entonces por el
A
A=C
X TX C
−1
.
(6.13)
Ahora veamos que
entonces T (vi )X
T es una matriz diagonal. Como T (vi ) = Avi = λi vi = 0v1 + · · · + λi vi + · · · + 0vn ,

X X
0
.
.
.
 
 
= λi , por tanto
 
.
 .. 
 
0
X TX
h
= T (v1 )
De la Ecuación (6.13) tenemos que A y
T (v2 )
X TX
···

λ1


0
T (vn ) = 
 ..
.

0
i

0
···
0
λ2
..
.
···
..
.
0
..
.
0
···
λn
son similares y de la ecuación (6.14),



.



X TX
(6.14)
es diagonal, por tanto
A es diagonalizable.
 
 

1
5
−5
 tiene vectores propios v1 =   y v2 =   de valores propios 2 y
Ejemplo 6.23. La matriz A = 
1
2
2 −3
-1, respectivamente (ver Ejemplo 6.2.)
h
i
Si tomamos la base X = {v1 , v2 } de R2 , formada por los valores propios de la matriz A, C = v1 v2 la

4
215
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

matriz de vectores propios y D = 
2
0
0

, entonces de acuerdo al Teorema 6.13 tenemos que
−1
A = CDC −1 .
Esto lo podemos verificar de la siguiente manera. De acuerdo al Teorema 6.11 la matriz
X AX
de A con respecto
a la base X esta dada por:
X AX
 
 

5
4
−5
1
−1
1
·
·
= C −1 AC = 
3 −2
2
2 −3
5
de donde C −1 AC = D y por tanto

 
2
0
1
 = D,
=
0 −1
1
A = CDC −1 .

3
−1
0
0





−1
3
0
0


Ejemplo 6.24. En el Ejemplo 6.6 calculamos los valores y vectores propios de la matriz A = 

 7 −1 −4
0


7 −1
0 −4
 
 


0
0
1/2
 
 


 
 


0
 0
−1/2






y encontramos que los vectores propios son v1 =   y v2 =   ambos de valor propio λ = −4, v3 = 

1
 0
 1/2 
 
 


0
1
1/2


1/2




1/2
 de valor propio λ = 2. Como A tiene cuatro vectores linealmente indepen
de valor propio λ = 4 y v4 = 

1/2


1/2
dientes entonces A es diagonalizable y A = CDC −1 con




0 0
1/2
1/2
−4
0 0 0








0 0 −1/2
 0 −4 0 0
1/2



C=
y
D
=




1 0
 0
1/2
1/2
0 4 0




0 1
1/2
1/2
0
0 0 2
Corolario 6.14. Si una matriz A de tamaño n×n tiene n valores propios distintos, entonces A es diagonalizable.


−2 −2 3




Ejemplo 6.25. (MatLab) La matriz A = −5
1 3 tiene tres valores propios diferentes, λ = −1, λ = 3


−6
0 5
y λ = 2. Esto lo podemos verificar en MatLab como se muestra a continuación
>> A = [−2 − 2 3; −5 1 3; −6 0 5]; f actor(poly(sym(A)))
ans =
-1
216
3
2

−1


Por tanto A es diagonalizable, de hecho A es similar a la matriz D =  0

0

0 0


3 0.

0 2
Teorema 6.15. Sea A una matriz de tamaño n×n, entonces A tiene n vectores propios linealmente independientes si y sólo si para cada valor propio λ, se tiene que
multiplicidad geométrica de λ = multiplicidad algebraica de λ.
En particular, si todos los valores propios de A son diferentes, todos los vectores propios de A son linealmente
independientes.
Demostración. Para comenzar la demostración, supongamos que A tiene k valores propios distintos, λ1 , . . . , λk ,
con multiplicidades n1 , . . . , nk , respectivamente. Es decir, el polinomio caracterı́stico de A está dado por pA (λ) =
(λ − λ1 )n1 · · · (λ − λk )nk , con n = n1 + · · · + nk .
“ ⇒”Supongamos que A tiene n vectores propios linealmente independientes, sean v11 , . . . , v1m1 , . . . ,
vk1 , . . . , vkmk estos vectores con m1 + · · · + mk = n y agrupados de tal forma que v11 , . . . , v1m1 tienen valor
propio λ1 , v21 , . . . , v2m2 tienen valor propio λ2 y, de manera inductiva, vk1 , . . . , vkmk tienen valor propio λk .
Como para i = 1, . . . , k, multiplicidad geométrica de λi ≤ multiplicidad algebraica de λi , entonces mi ≤ ni ,
ahora si mi < ni para algún i = 1, . . . , k entonces tenemos que
n = m1 + · · · + mk < n1 + · · · + nk = n,
lo cual es imposible, por tanto para todo i = 1, . . . , k, mi = ni , es decir, para todo i = 1, . . . , k tenemos que
multiplicidad geométrica de λi = multiplicidad algebraica de λi .
“ ⇐”Supongamos que la multiplicidad geométrica de cada valor propio es igual a la multiplicidad algebraica,
entonces dim(Eλj ) = nj , para 1 ≤ j ≤ k. Sean {v11 , . . . , v1n1 }, {v21 , . . . , v2n2 }, . . . ,
{vk1 , . . . , vknk } bases para Eλ1 , Eλ2 , . . . , Eλk , respectivamente.
Veamos que los vectores v11 , . . . , v1n1 , v21 , . . . , v2n2 , · · · , vk1 , . . . , vknk son linealmente independientes.
Supongamos que
α11 v11 + · · · + α1n1 v1n1 + · · · + αk1 vk1 + · · · + αknk vknk = 0
(6.15)
y sean v1 = α11 v11 + · · · + α1n1 v1n1 , . . . , vk = αk1 vk1 + · · · + αknk vknk , entonces la ecuación (6.15) se convierte
en
v1 + v2 + · · · + vk = 0.
(6.16)
Afirmación: v1 = v2 = · · · = vk = 0
Supongamos que algunos de los vj 6= 0, como vij ∈ Eλi para 1 ≤ i ≤ k entonces tenemos que v1 ∈ Eλ1 ,
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
217
v2 ∈ Eλ2 , . . . , vk ∈ Eλk , entonces los vectores de la lista v1 , . . . , vk que son no nulos, son vectores propios de
valores propios λ1 , . . . , λk , respectivamente. Como los valores propios λ1 , . . . , λk son distintos, entonces, por el
Teorema 6.4, los vectores no nulos de la lista v1 , . . . , vk son linealmente independientes, pero de la Ecuación (6.16)
se sigue que estos vectores son linealmente dependientes, lo cual es contradictorio y por tanto v1 = · · · = vk = 0,
y la afirmación se cumple.
Luego para 1 ≤ j ≤ k tenemos que
0 = vj = αj1 vj1 + · · · + αjn1 vjnj ,
pero como los vectores {vj1 , . . . , vjnj } son una base para Eλj , entonces son linealmente independientes y por
tanto αj1 = · · · = αjnj = 0. Como esto es para todo j = 1, . . . , k tenemos que
α11 = · · · = α1n1 = · · · = αk1 = · · · = αknk = 0.
Entonces los vectores v11 , . . . , v1n1 , v21 , . . . , v2n2 , . . . , vk1 , . . . , vknk son linealmente independientes y como todos estos son vectores propios de A y n1 + · · · + nk = n, entonces A tiene n vectores propios linealmente
independientes.
Corolario 6.16. Sea A una matriz A de tamaño n×n, entonces A es diagonalizable si y sólo si para todo valor
propio λ de A se cumple que
multiplicidad geométrica de λ = multiplicidad algebraica de λ.
Demostración. El corolario se sigue de los Teoremas 6.13 y 6.15.
Ejemplo
6.26.
1. En el Ejemplo
6.6 vimos que la matriz


3 −1
0
0




−1
3
0
0
 tiene valores propios λ = −4, λ = 4 y λ = 2 y que las multiplicidades geométricas y

A=

 7 −1 −4
0


7 −1
0 −4
algebraicas eran a−4 = g−4 = 2, a4 = g4 = 1 y a2 = g2 = 1, entonces la matriz es diagonalizable.


−3 −2
1




2. En el Ejemplo 6.7 vimos que el único valor propio de la matriz A =  1 −6
1  es λ = −4 con multplicidad


1 −2 −3
algebraica a−4 = 3 y geométrica g−4 = 2, entonces por el corolario anterior A no es diagonalizable.


−4 −1
1




3. En el Ejemplo 6.8 vimos que el único valor propio de la matriz A =  0 −5
1  es λ = −4 con multiplicidad


−1
0 −3
algebraica es a−4 = 3 y geométrica g−4 = 1, por tanto A no es diagonalizable.
6.4.1. Para cada una de las matrices del problema 6.1.1 determine si es diagonalizable. En caso afirmativo,
encuentre las matrices C y D tal que A = CDC −1 .
218
6.5.
Matrices Simétricas y Diagonalización Ortogonal

a11

 ..
Definición 6.10. Sea A =  .

am1
···
..
.
···

a1n

.. 
de tamaño m × n con entradas complejas.
. 

amn
1. Definimos la matriz conjugada de A, denotada por A, como la matriz que se obtiene al conjugar las entradas de
A, estos es

a11

 .
A =  ..

am1
···
..
.
···

a1n

.. 
. 

amn
t
2. La transpuesta hermitiana de A, denotada por AH , se define como AH = A .
3. Decimos que A es hermitiana si A = AH .

Ejemplo 6.27. Considere la matriz A = 
t

AH = A = 
1
1−i
1+i
2

1
1−i
1+i
2


, nótese que A = 
1
1−i
1+i
2


=
1
1+i
1−i
2

y
. Como A = AH entonces A es una matriz hermitiana.
Teorema 6.17. Sea A una matriz hermitiana de tamaño n×n entonces los valores propios de A son reales.
Esto es, si λ es un valor propio de A entonces λ ∈ R. En particular, si A una matriz simétrica con entradas
reales, entonces sus valores propios son reales y por tanto sus vectores propios son reales.
t
Demostración. Como A es hermitiana, entonces A = AH = A de donde At = A, entonces
t
λv · v = λv t v = v t λv Av = v t Av = v t AH v = v t A v = (Av)t v
= (Av)t v = (λv)t v = λv t v = λv · v.
De donde se sigue que (λ − λ)v · v = 0, como v 6= 0 entonces v · v 6= 0. Por tanto λ − λ, es decir λ = λ.
Teorema 6.18. Sea A una matriz hermitiana de tamaño n×n y sean x y y vectores propios de valores propios
λ1 y λ2 , respectivamente. Si λ1 6= λ2 entonces x · y = 0, es decir, x y y son ortogonales. El teorema también se
cumple si A es una matriz simétrica con entradas reales.
Demostración.
λ1 (v1 · v2 ) = (λ1 v1 · v2 ) = (Av1 · v2 ) = (Av1 )t v2 = (Av1 )t v2
t
= v1 t |{z}
A v2 = v1 t Av2 = v1 t λ2 v2 = λ2 v1 t v2 = λ2 (v1 · v2 ).
AH =A
Luego (λ1 − λ2 )v1 · v2 = 0, como λ1 6= λ2 entonces v1 · v2 = 0.
219
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO

1
. Los valores propios de A son λ = 1 y λ = 3 los cuales son números reales y
Ejemplo 6.28. Sea A = 
1 2
 
 
1
1
los vectores propios son v1 =   y v2 =  . Nótese que v1 · v2 = 0.
1
−1


2 −1 −1




Ejemplo 6.29. La matriz simétrica A = −1
2 −1 debe tener valores propios reales, usamos MatLab


−1 −1
2
para calcular la factorización de su polinomio caracterı́stico:

2
>> A = [2 − 1 − 1; −1 2 − 1; −1 − 1 2]; f actor(poly(sym(A)))
ans =
x ∗ (x − 3)2
Por tanto los valores propios son λ = 0 y λ = 2 de multiplicidad 2.
6.6.
Formas Cuadráticas
Definición 6.11. Una forma cuadrática es una expresión de la forma
n
X
i=1
aii x2i +
X
aij xi xj .
i<j

a11

 a12
 2
2
t
aii xi +
Nótese que si F =
aij xi xj es una forma cuadrática entonces F = x Qx donde Q = 
 ..
 .
i=1
i<j

n
X

X
a1n
2

a12
2
···
a22
..
.
···
..
.
a2n
2
···
x1
 
 .. 
y x =  . .
 
xn
2
2
Ejemplo
 forma caudrática F = 2x + 2xy + 2y se puede escribir matricialmente como F =
  La
 6.30.
h
i 2 1
x
  .
x y 
y
1 2
Observación 6.3. Un hecho muy conocido, pero que no será demostrado en este libro, es que toda matriz
simétrica es diagonalizable, esto hecho lo usaremos en el siguiente teorema.
Teorema 6.19. (Teorema de los ejes principales) Sea F = xt Qx un forma cuadrática en n variables con Q una
matriz simétrica. Como Q es diagonalizable existen vectores propios v1 , . . . , vn de Q linealmente independientes.
Sean λ1 , . . . , λn los respectivos valores propios correspondientes a v1 , . . . , vn y sea X = {v1 , . . . , vn }, entonces
X es una base de Rn . Entonces bajo la base X, la forma cuadrática tiene la forma:
F = λ1 y12 + · · · + λn yn2 .

a1n
2 
a2n 
2 

.. 
. 

ann
220
Demostración. Primero veamos que a la base X la podemos tomar ortonormal.
Si los λi son todos distintos, entonces los vectores propios son ortogonales y X es ortogonal, si no lo son,
tomamos v11 , . . . , v1k1 , . . . , vs1 , . . . , vsks una reindexación de los vectores de X de tal manera que v11 , . . . , v1k1 son
vectores propios de valor propio λ1 ,. . . vs1 , . . . , vsks vectores propios de valores propios λs . Aplicando GrammSchmidt a cada uno de los conjuntos {v11 , . . . , v1k1 , }, . . . ,
{vs1 , . . . , vsks } obtenemos vectores w11 , . . . , w1k1 , . . . ,ws1 , . . . , wsks formando una base ortogonal y redefinimos
1
1
1
1
w1k1 , . . . ,
wsks .
w11 , . . . ,
ws1 , . . . ,
X=
||w11 ||
||w1k1 ||
||ws1 ||
||wsks ||
Por tanto X es ortonormal.
Como X es una base de vectores propios entonces

λ1

 ..
X QX =  .

0
Además sabemos que
X QX
h
= BQB −1 donde B = v1
matriz ortogonal y B −1 = B t , por tanto
Q = B −1

···
..
.
0
..
.
···
λn
···
i
vn . Como X es ortonormal, entonces B es una
X QX B


.

(6.17)
t
= BX
QX B
(6.18)
Definamos y = Bx y sean y1 , . . . , yn las componentes de y, entonces de (6.18) tenemos que la forma cuadrática
tiene la forma
F = xt Qx = xt B t
X QX Bx
= (Bx)t
X QX Bx
= yt
X QX y.
(6.19)
Luego de (6.17) y (6.19) tenemos que
F = λ1 y12 + · · · + λn yn2 .
Además nótese que los ejes de esta forma cuadrática son los vectores de la base X, los cuales son perpendiculares.
Observación 6.4. Una ecuación de la forma F = c con F una forma cuadrática y c una constante es una
sección cónica.
El teorema de los ejes principales nos permite identificar la secciones cónicas. Sea xt Qx = c una cónica con
c > 0 constante y sean λ1 , . . . , λ2 los valores propios de Q, entonces tenemos lo siguiente:
Si Q es 2x2 y:
1. λ1 , λ2 > 0 entonces xt Qx = c es una elipse.
2. λ1 , λ2 < 0 entonces xt Qx = c es vacia.
3. λ1 · λ2 < 0 entonces xt Qx = c es una hipérbola.
4. λ1 · λ2 = 0 entonces xt Qx = c es una forma degenerada.
221
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
En el caso 3x3 tenemos:
1. Si λ1 , λ2 , λ3 > 0 entonces xt Qx = c es un elipsoide.
2. Si λ1 , λ2 , λ3 < 0 entonces xt Qx = c es vacia.
3. Si uno de los λi es positivo y los otros negativos entonces xt Qx = c es un hiperboloide de 2 hojas
4. Si uno de los λi es negativo y los otros positivos, entonces xt Qx = c es un hiperboloide de una hoja.
5. Si c = 0 y uno de los λi es positivo y los otros negativos o dos positivos y uno negativo entonces xt Qx = c es
un cono.
Ahora consideremos la ecuación z = xt Qx con z variable y Q de tamanño 2x2 con valores propios λ1 y λ2 .
Entonces tenemos lo siguiente
1. Si λ1 · λ2 > 0 entonces z = xt Qx es un paraboloide elı́ptico.
2. Si λ1 · λ2 < 0 entonces z = xt Qx es un paraboloide hiperbólico o silla de montar.
 

i 2 1
x
  =
Ejemplo 6.31. La sección cónica 2x2 +2xy+2y 2 = 4 se puede escribir matricialmente en la forma x y 
y
1 2
4.
 
 


1
1
2 1
 son v1 =   y v2 =   con valores propios 1 y 3, respectivamente.
Los vectores propios de Q = 
1
−1
1 2
Entonces con respecto a la base X = {v1 , v2 } tenemos que la ecuación de la forma cuadrática está dada por
h
x′2 + 3y ′2 = 4 cuya ecuación corresponde a una elipse.
Ahora, si consideramos la ecuación z = 2x2 + 2xy + 2y 2 entonces con respecto a la base X la ecuación tiene
la forma z = x′2 + 3y ′2 el cual corresponde a un paraboloide elı́ptico.
h
Ejemplo 6.32. La sección cónica 4xy = 5 se puede escribir matricialmente en la forma x
5.
 

i 0 2
x
  =
y 
y
2 0
 
1
 son v1 =   y v2 =   con valores propios
Los vectores propios de Q = 
1
−1
2 0
-2 y 2, respectivamente. Normalizando estos vectores obtenemos w1 = √12 v1 y w2 = √12 v2 , entonces con respecto

0 2


1

a la base X = {w1 , w2 } tenemos que la ecuación de la sección cónica está dada por −2x′2 + 2y ′2 = 5 cuya
ecuación corresponde a una hipérbola abierta
la dirección de y ′ , es decir,
√ en 
 en la dirección de la linea generada
√
√
√
√
− 5/2
5/2
 y − √5 w 2 =  √
.
por v2 y con interceptos √52 w2 = 25 v2 = √
2
− 5/2
5/2
Ahora, si consideramos la ecuación z = 4xy entonces con respecto a la base X la ecuación tiene la forma
z = −2x′2 + 2y ′2 la cual corresponde a un paraboloide hiperbólico o silla de montar.


5 −1 −1




Ejemplo 6.33. (MatLab) Sea Q = −1
5 −1, determinar que tipo de cónica corresponde a la ecuación


−1 −1
5
xt Qx = 5.
222
Solución. Usamos MatLab para calcular los valores propios de A,
>> A = [5 − 1 − 1; −1 5 − 1; −1 − 1 5]; eig(A)
ans =
6
3
6
Por tanto la cónica corresponde
a un elipsoide. Para calcular
calculamos los vectores
 coordenados,

  los ejes
 
−1
−1
1
 
 
 
 
 
 
propios los cuales son v1 = 1 con valor propio 3 y v2 =  1  y v3 =  0  ambos de valor propio 6. Nótese
 
 
 
1
0
1
que v2 y v3 no son ortogonales, pero estos forman una base
para
el
subespacio
propio E6 , entonces usando


−1/2




Gramm-Schmidt, reemplazamos v3 por w3 = v3 − proyv2 v3 = −1/2. Obtenemos que los ejes coordenados bajo


1
los cuales la gráfica de xt Qx = 5 es un elipsoide son las lineas determinadas por los vectores:
 
1
 
 
v 1 =  1 ,
 
1

−1


Ejemplo 6.34. Sea Q =  5

−1
5
−1

−1

 
 
v2 =  1 
 
0
y

−1/2





w3 = −1/2 .


1



−1 −1, determinar que tipo de cónica corresponde a la ecuación xt Qx = 5.

−1
5
Solución. Se puede ver que los valores propios de Q son λ = 3, 6 y −6. Por tanto la cónica corresponde a un
hiperboloide de una hoja.


 
−1/2
1


 


 
Es fácil ver que los vectores propios de Q son v1 = 1 con valor propio 3, v2 = −1/2 de valor propio


 
1
1
 
−1
 
 
6 y v3 =  1  de valor propio -6. De donde se sigue que la ecuación de esta cónica con respecto a la base
 
0
{v1 , v2 , v3 } es 3x′2 + 6y ′2 − 6z ′2 = 5, la cual corresponde a un hiperboloide de una hoja cuyo eje central es la
linea generada por el vector v3 .
Ejemplo 6.35. Determine el tipo de cónica determinada

0


Solución. La matriz de la forma cuadrática es Q = 1

1
por la cuadrática 2xy + 2xz + 2yz = 5.

1 1


0 1 cuyos vectores propios ortogonales son v1 =

1 0
223
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
 



1
−1/2
−1
 


 
 


 
 1  y v2 = −1/2 ambos de valor propio -1 y v3 = 1 de valor propio 2. Por tanto la ecuación de esta
 


 
1
1
0
cónica con respecto a la base {v1 , v2 , v3 } es −x′2 − y ′2 + 2z ′2 = 5 cuya gráfica corresponde a un paraboloide de

dos hojas cuyo eje central es la linea generada por el vector v3 .
6.7.
Ejercicios
En los problemas 4-8 λ1 , λ2 , . . . , λn son los valores propios de una matriz A. Encuentre una matriz ortogonal
Q y una matriz diagonal D tal que A = QDQt si:

a. A = 
3
4
4


−3

b. A = 
3
2

2

3

3 1


c. A = 1 3

0 0

0


0

2

1 3


d. A = 3 1

0 0

0


0

1
Para cada una de las matrices del problema anterior identifique el tipo de cónica representada por la forma
cuadrática xt Ax = 4 y bosquejar su grafica. Para las matrices dadas en los Problemas 1a. y 1b. identifique el
tipo de superficie que que representa la ecuación z = xt Ax con z variable. Para cada una de las matrices del
1 encuentre
vectores propios
A
X . Sean
Problema

 
y encuentre
 una

 baseX de
 la matrizX 







1
1
0
0
−1 
1 


 

 
 

 
 

 

 
 
 
 
 
 
X = x1 = −1 , x2 =  1  , x3 =  0  y Y = y1 = 1 , y2 = 1 , y3 = 0 bases de R3 .


 
 
 
 
 
 










0
0
−1
1
2 
1 
Encuentre las matrices de cambio 
de base Y IX 
y X IY . Sea T : R3 −→ R2 la transformación lineal cuya matriz
−1 1
1
. Calcular la matriz Z TX de T con respecto a las bases
−1

 

 


 
 


−1 
0
1


 

 
 

0 
1
 
 
 
X = x1 = −1 , x2 =  1  , x3 =  0  de R3 y Z = z1 =   , z2 =   de R2 . Sea


 
 
 


1 
−1



2 
−1
0


−1 1
0




T : R3 −→ R3 la transformación lineal cuya matriz E TE está dada por E TE =  0 2 −1. Calcular la


1 0 −1

 
 
 



−1 
0
1


 
 
 

 
 
 
matriz X TX de T con respecto a la base X = x1 = −1 , x2 =  1  , x3 =  0  de R3 .

 
 
 





2 
−1
0
7.
6.
5.
4.
3.
2.
1. Mas Problemas.

 
 
 



−1 
0
1


 
 

 
 
 
 
8. Sea X = x1 = −1 , x2 =  1  , x3 =  0  una base de R3 , encontrar una base Y = {y1 , y2 , y3 } tal

 
 
 





2 
−1
0
E TE
está dada por
E TE
=
0

2
224
que
X IY

1 0


= 1 1

0 1

1


0.

1

1
0 1





=  1 1 0 .


0 1 1

 
 

0 
1
10. Sea T : R3 −→ R2 una transformación lineal y sea Z = z1 =   , z2 =   una base para R2 y X =

1 
−1

 
 
 





1
0
−1 

 

 
 

−1
1
1
 
 
 
, calcular la matriz E TE .
x1 = −1 , x2 =  1  , x3 =  0  una base para R3 . Si Z TX = 





 


0
2
−1



0
−1
2 

 
 

   

0 
1
x
+
2y
x
 y sea Y = y1 =   , y2 =   una base de R2 .
11. Sea T : R2 −→ R2 definida por T   = 

1 
−1
2x + y
y


−1 1
.
Calcular la base X tal que Y TX = 
0 2




1
1
2
1
.
 . Demuestre que no existe una base X tal que X TX = 
12. Sea T : R2 −→ R2 tal que E TE = 
0 1
1 1
9. Repetir el problema anterior si en lugar de
X IY
se nos da
Y IX
Capı́tulo 7
Aplicaciones
En esta sección asumiremos
que A

λ1 0 · · ·


 0 λ2 · · ·
vectores propios y D = 
.. . .
 ..
.
.
.

0
7.1.
0
···
−1
es una
donde C es la matriz de
 matriz diagonalizabe con A = CDC
0


0

..  con λ1 , . . . , λn los valores propios de A.
. 

λn
Potencia de una matriz
Es fácil ver que Ak = CDk C −1 . De hecho si suponemos por inducción que Ak−1 = CDk−1 C −1 entonces
−1
k−1
Ak = Ak−1 A = CDk−1 |C −1
DC −1 = CDk C −1 .
{z C} DC = CD
=I

λk1


0
También se puede ver facilmente por inducción que Dk = 
 ..
.

0
0
λk2
..
.
0

Ejemplo 7.1. Calcule la k-ésima potencia de la matriz A = 
2 1
1 2

···
0
···
..
.
0
..
.
···
λkn








.
 
1
Se puede ver que los vectores propios de A son v1 =   de valor propio λ = 1 y v3 =   de valor propio
1
−1
λ = 3, entonces tenemos que

−1


1
1
3 0
1
1



A=
1 −1
0 1
1 −1

1

3k

Por tanto

Ak = 
1
1
1

3 0
k 
1
1
−1

 

1 −1
0 1
−1

=
1
1
1 −1

225
0
 
 
1 k
1
(3 + 1)
0 1 1
 = 2
 
1
k
1 2 1 −1
2 (3 − 1)
1 k
2 (3
1 k
2 (3
− 1)
+ 1)

.
226
7.1.1.
Relaciones de recurrencia
Si se tiene una relación de recurrencia determinada por una ecuación de la forma an = αan−1 + βan−2 ,
entonces tenemos el sistema de ecuaciones



 


an = αan−1 + βan−2 ,
an−1
α β
an
,

=
El cual es equivalente al sistema 

an−1 = an−1 ,
1 0
an−2
an−1


α β
 y si continuamos aplicando el sistema a los vectores
el cual es cierto para todo n. Si hacemos A = 
1 0

 

an−2
an−1
 , . . . , obtenemos
, 

an−3
an−2


 
an
a

 = An−1  1  .
(7.1)
an−1
a0
Si conocemos los valores de a1 y a0 , entonces con la Ecuación
una fórmula para an en términos

 (7.1) obtenemos
λ1 0
 C −1 , con C la matriz de vectores propios
de los valores propios de A y n. Esto se da porque si A = C 
0 λ2


n−1
λ
0
1
 C −1 .
y λ1 y λ2 los valores propios de A, entonces An−1 = C 
n−1
0
λ2
Ejemplo 7.2. (Suceción de Fibonacci) La secuencia de Fibonacci satisface la relación Fn = Fn−1 + Fn−2 ,
para n ≥ 2, con F0 = 0 y F1 = 1. Encuentre una fórmula para calcular el n-ésimo término
Fn . 




Fn−1
1 1
Fn


=
De acuerdo a las ecuaciones Fn = Fn−1 +Fn−2 y Fn−1 = Fn−1 , tenemos el sistema 
1 0
Fn−2
Fn−1
y por tanto


 



Los vectores propios de A son v1 =
valor propio λ1 = 12 (1 +
√
5).
Fn
Fn−1

1
2
Por tanto A = CDC −1 con C =
obtenemos que

1
2
 = An−1 
F1
F0
 , con A = 
1 1
1 0
.

√ 
√ 
1
√
5
5
1
+
 con valor propio λ1 = 1 (1 − 5) y v2 =  2
 con
2
1
1
1−
1−
1
√ 5
1
2

√ 
√ 1
1− 5
5
 y D = 2
0
1
1+
 
1
 = An−1   = CDn−1 C −1  

0
F0
Fn−1


 
√ n−1
1
0
1
−
1
5
−1
=C 2
√ n−1  C  
1
0
0
5
2 1−


√ n
√ n
5
1
√1
− √15 12 − 25
2 + 2
=  5
√ n−1
√ n−1 
5
5
1
1
√1
√1
+
−
−
2
2
5 2
5 2

Fn


F1

0
1
2
1+

√  y de estos
5
227
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
De esto concluimos que Fn =
7.1.2.
√1
5
1
2
+
√
5
2
n
−
√1
5
1
2
−
√
5
2
n
Cadenas de Markov
Esta subsección también se trata de una aplicación de la potencia de matrices y lo expondremos con ejemplos.
Ejemplo 7.3. Dos compañias A y B manipulan el mercado de celulares y se calcula que A tiene el 60 % de los
clientes, mientras que B maneja el 40 % del mercado. La compañia A prepara una agresiva campaña comercial
la cual, de acuerdo a un estudio de mercado, acarreará las siguientes consecuencias:
El 90 % de los clientes de A permancerán con A y el resto se irá a B
El 30 % de los clientes de B se cambiarán a A y el resto permanecerá con B.
Determine los porcentajes de clientes de A y B si se aplica la campaña 1 vez, 10 veces, k veces e indefinidamente.
Si Xk y Yk es el porcentaje de clientes de A y B respectivamente después de aplicar la campaña k veces
entonces tenemos que
Xk = 0,9Xk−1 + 0,3Yk−1
Yk = 0,1Xk−1 + 0,7Yk−1

equivalentemente 
Xk
Yk


=
0,9
0,1


0,3 Xk−1
.

0,7
Yk−1
Por tanto, despues de aplicar la campaña una vez otbtenemos

  
  
  
0,66
0,6
0,9 0,3
X0
0,9 0,3
X1
.
  = 
  = 
 =
0,34
0,4
0,1 0,7
Y0
0,1 0,7
Y1
Es decir, A manejará el 66 % de los clientes y B el 34 %.
Si se aplica la campaña 10 veces obtenemos que


X10
Y10


=
0,9 0,3
0,1 0,7


X9
Y9


=
0,9 0,3
0,1 0,7
2 
 
X8
Y8


 = ··· = 
0,9 0,3
0,1 0,7
10 


X0
Y0


=
0,749
0,251

.
Es decir, después de aplicar la campaña 10 veces, A dominará


 mercado.
 
  el 74.9% del
0,9
0,3
,6
X
Xk
0
.
Despueś de aplicar la campaña k veces obtenemos que   = Ak   = Ak  , donde A = 
0,1 0,7
,4
Y0
Yk
Para determinar
 potencia de A calculamos los valores y vectores propios y encontramos que los
  la k-ésima
−1
3
vectores v1 =   y v2 =   de valores propios λ = 1 y λ = 0,6, respectivamente, por tanto: A = CDC −1
1
1




1 0
3 −1
. De lo cual se obtiene que
yD=
con C = 
0 0,6
1
1

Ak = CDk C −1 = 
3
1

 
−1
1
0
1

1
k 4
1
0 0,6
−1
 
1
3 + 0,6k
1
 = 4
1
k
3
4 1 − 0,6
3
4
1
4


1 + 3 · 0,6k
1 − 0,6k
228
De esta forma tenemos que


Xk
Yk


 = Ak 
0, 6
0, 4

=

1
4
1
4
3 − 0,6k+1
1 + 0,6k+1


Por tanto el porcentaje de clientes de A después de aplicar la campaña k veces serı́a el
B serı́a 41 1 + 0,6k+1
1
4
3 − 0,6k+1 % y el de
Esto indica que si se aplica la campaña indefinidamente el máximo porcentaje de clientes que obtiene A es
1
1
3 − 0,6k+1 = 0,75 % y el mı́nimo porcentaje al que B llegarı́a es Y∞ = lı́m
3 + 0,6k+1 =
X∞ = lı́m
k→∞ 4
k→∞ 4
0,25 %.
Comparando este último resultado con el obtenido al aplicar la campaña 10 veces obtenemos que es suficiente
con aplicar esta alrededor de 10 veces para obener un buen beneficio para la compañia.
7.2.
Exponencial de una matriz diagonalizable
La función exponencial de un real x, se define como la serie ex =
convergente para todo x ∈ R y por tanto ex está bien definido para todo x.
∞
X
1 k
x . Se sabe que esta serie es
k!
k=0
∞
X
1 k
A y
k!
k=0
mostraremos en esta sección que esta matriz está bien definida si A es diagonalizable. En general la matriz de
De igual forma para una matriz A definiremos la matriz exponencial como la matriz eA =
cualquier matriz compleja está bien definida, pero esto requiere de la forma de Jordan, en esta sección solo nos
concentraremos en las matrices diagonalizables.


λ1 0 · · · 0




 0 λ2 · · · 0 


Primero, si D =  .
.. . .
..  es diagonal, entonces
 ..

.
.
.


0
0 · · · λn
eD

λk1


∞
∞
X
0
1 k X 1 

D =
=
.
k!
k! 
 ..
k=0
k=0

0
∞
X 1
λk1
0

k=0 k!

∞

X
1 k

0
λ2

k!
=
k=0

..
..


.
.



0
0
0
λk2
..
.
0
···
···
..
.
···
···
···
..
.
···
0
0

λk1
0
λk2
..
.
···
···
..
.
0
..
.
0
···
λkn
0
eλ 2
..
.
···
···
..
.
0
..
.
0
···
eλ n




∞
 X
0
1
=


.
 k=0 k!  ..


λkn
0

0
..
.
 

eλ 1

 
 
0
  0
=
  ..
..
  .
 
.

∞
0
X 1 
k
λn
k!
k=0

0
0
















229
Autor: OMAR DARÍO SALDARRIAGA, HERNÁN GIRALDO
Ahora, si la matriz A es diagonalizable con A = CDC −1 , tenemos que:
∞
∞
∞
X
X
1
1 k X 1
−1 k
A =
(CDC ) =
CDk C −1 = C
k!
k!
k!
k=0
k=0
k=0
por tanto eA está bien definido y eA = CeD C −1 .


2
1
.
Ejemplo 7.4. Calcular eA si A = 
1 2

En el Ejemplo 7.1 vimos que A = CDC −1 con C = 

eA = CeD C −1 = 
7.2.1.
∞
X
1 k
D
k!
1
1
1 −1


1
1
1 −1
e3
0
0
e


1
k=0


yD=
1
1 −1
−1

3
0

=
!
C −1 = CeD C −1 ,

0
. Entonces
1
e4
e2
e4
e−2


Sistemas Lineales de Ecuaciones diferenciales
Considere el sistema lineal de ecuaciones diferenciales de la forma



x′1 = a11 x1 + · · · + a1n xn ,



..
.




x′ = a x + · · · + a x ,
n1 1
nn n
n
 
a11
x′1
  
 ..   ..
El cual es equivalente al sistema  .  =  .
  
an1
x′n



a11
x1

 
.
.



el cual también, por simplicidad, escribiremos X ′ = AX con X =  ..  y A =  ..

 
an1
xn
Si A es diagonalizable con A = CDC −1 entonces el sistema tenemos que

···
..
.
···
···
..
.
···
 
x1
a1n
 
..   .. 
 ,
. 
 . 
xn
ann

a1n

.. 
.
. 

ann
X ′ = AX = CDC −1 X o equivalentemente C −1 X ′ = DC −1 X o equivalentemente Y ′ = DY
donde Y = C −1 X y por tanto Y ′ = C −1 Y ′ . Si denotamos por y1 , . . . , yn las coordenadas del vector Y , entonces
la ecuación Y ′ = DY produce el sistema de ecuaciones
y1′ = λ1 y1 ,
...,
yn = λn yn
cuyas soluciones están dadas por
y 1 = c 1 eλ 1 t ,
...,
y n = eλ n t .
Como X = CY , obtenemos la siguiente solución al sistema inicial
 


x1
c 1 eλ 1 t
 


 .. 
 . 
 .  = X = CY = C  ..  .
 


xn
c 1 eλ 1 t
230
Ejemplo 7.5. Resolver el sistema de ecuaciones lineales


x′ = 2x1 + x2 ,
1

x′ = x1 + 2x2 .
2
 
  
x
2 1
x′1
  1  y por el Ejemplo 7.1 sabemos que la matriz
El sistema se puede escribir en la forma   = 
′
1 2
x2
x2






3
0
1
1
2 1
.
yD=
 se puede escribir como el producto A = CDC −1 con C = 
A=
0 1
1 −1
1 2
 

 
′
y
3
0
y
1
  1  cuyas
Entonces haciendo Y = C −1 X obtenemos el sistema Y ′ = DY , es decir,   = 
0 1
y2
y2′
soluciones están dadas por
y1 = c1 e3t
y
y 2 = c 2 et
con c1 y c2 constantes. Finalmente obtenemos la solución



 
 
 
c1 e3t + c2 et
c1 e3t
1
1
c1 e3t
x1

.
=
=
 =C
c1 e3t − c2 et
1 −1
c 2 et
c 2 et
x2
Es decir, las solución al sistema está dada por
x1 = c1 e3t + c2 et
con c1 y c2 constantes.
y
x2 = c1 e3t − c2 et