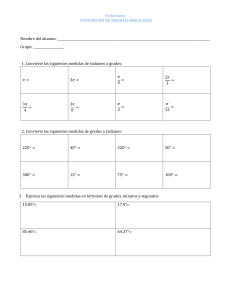
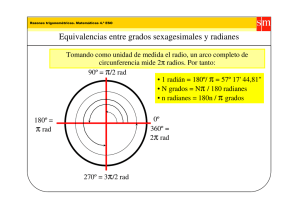
y(x1,t) = A = y(x 2,t + − t T) = 2 ( − t+ ) = − t = 1 − t+ = 1 x2 − x1 =
Anuncio

(J-04) Por una cuerda se propaga un movimiento ondulatorio caracterizado por la función de onda y = ASen2( x − Tt ) Razone a qué distancia se encuentran dos puntos de esa cuerda si: a) La diferencia de fase entre ellos es de radianes, b) Alcanzan la máxima elongación con un retardo de un cuarto de periodo. ................................. a) Si en un instante determinado la diferencia de fase entre dos puntos es radianes entonces: x 2( 2 − t T) − x 2( 1 − t T) = x −x 2 2 1 = d x2 − x1 = 2 La respuesta a la cuestión puede ser muy rápida y evidente si tenemos en cuenta que a una distancia de m corresponde una diferencia de fase de 2 radianes ( y a radianes 2 m. Figura de abajo) y(x,0) 2π para t=0 , y(x,0)=ASen x λ 2π λ x λ 3λ Fase= λ 4 2 4 λ x π 2 π 3π 2π 2 Fase A) Si dos puntos del medio alcanzan la máxima elongación con un retardo de un cuarto de periodo: x1 T 4 ) d2( y(x 1 , t) = A = y(x 2 , t + x1 − t T = x2 1 y 4 − t+ T4 T − t T) = x 2( 2 − t+ T4 T )= 2 = 1 t 4 . Eliminando del sistema anterior T se obtiene: x 2 − x 1 = 4 La respuesta a la cuestión podría se rápida, quizá demasiado, si tenemos en cuenta que a un tiempo de un cuarto de período corresponde una distancia recorrida de un cuarto de longitud de onda La gráfica que se adjunta quizá aclare la cuestión: y(x,0) 2π para t=0 , y(x,0)=ASen x λ 2π x Fase= λ 1 * 2 *1 2 λ x λ 2 Desplazamiento hacia dcha. con v = λ Τ Cuando 1 esté en *1(un cuarto de período) 2 estará en *2 (un cuarto de período) . En la figura se observa que la distancia (x) entre 1 y 2 es λ 4