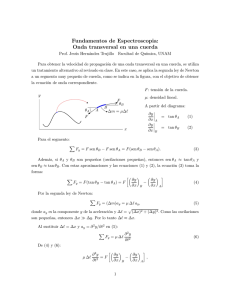
Un extremo de una cuerda tensa horizontal de 4 m de longitud tiene

CASTILLA LA MANCHA / JUNIO99. LOGSE / FÍSICA / VIBRACIONES Y
ONDAS/OPCIÓN A/PR. 1
Un extremo de una cuerda tensa horizontal de 4 m de longitud tiene un movimiento
oscilatorio armónico de dirección vertical; en el instante t = 0,3 s la elongación de ese
extremo es 2 cm. Se mide que la perturbación tarda en llegar de un extremo al otro de la
cuerda 0,9 s y que la distancia entre dos mínimos consecutivos es 1 m. Calcular:
a) La amplitud del movimiento ondulatorio
b) La velocidad del punto medio de la cuerda en el instante t = 1s.
c) el desfase entre dos puntos separados 1,5 m, en un instante dado.
a) La amplitud del movimiento es la misma que la del extremo, y por tanto es de 2 cm.
b) Para determinar la velocidad de un punto de la cuerda es necesario determinar la ecuación de
la oscilación.
La longitud de onda de la misma es de 1 m.
λ
Para determinar el periodo hay que hacer uso de la velocidad de propagación que es: v =
T
λ
1
Por tanto: T = =
= 0,225 s
v 4 / 0,9
2·π 

2· π 
2 · π
La ecuación de onda es: y = A · sen 
·x−
· t  = 0,02 · sen  2 · π · x −
· t
T
0,225 
 λ


Por tanto, la velocidad transversal, derivada de la elongación con respecto al tiempo será:
dy
2· π

2· π 

2· π 
v=
= −0,02 ·
· cos  2 · π · x −
· t  = −0,56 · cos 2 · π · x −
· t
dt
0,225
0,225 
0,225 


Para la posición x = 2 m y t = 1 s, la velocidad tiene un valor: v = 0,53 m/s.
c) El desfase entre dos puntos, para una longitud de onda de 1 m es:
desfase = fase1 – fase2 = 2 · π · ∆x = 3 π = π
www.profes.net es un servicio gratuito de Ediciones SM