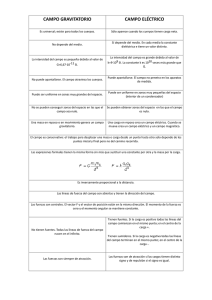
Campo gravitatorio

CONCEPTO DE CAMPO. INTERACCIÓN A DISTANCIA
La interacción entre dos partículas puede hacerse de dos maneras:
•
•
Por contacto entre ellas, que sería el caso de dos bolas que chocan
Por acción a distancia, esto es, perturbando las propiedades del medio donde se
encuentran las partículas. Supongamos a la tierra como una masa aislada, decimos que
ella crea un campo (campo de fuerzas gravitatorio) porque produce una perturbación
en el espacio que la rodea, de tal manera que si en él colocamos otra masa, se verá
sometida a una fuerza (que le llamamos peso). Dicho de otra forma, la tierra ejerce una
fuerza sobre la otra masa a distancia, sin necesidad de tocarla.
Para hacernos una idea clara de lo que es un campo, piensa en una fuente sonora, como una
radio. Cuando está en funcionamiento, continuamente emite ondas sonoras que se propagan
por el espacio que la rodea. Podemos decir que en ese espacio hay un campo de sonido. Ahora
vamos a reparar que significa eso:
1. Se necesita un agente que cree el campo. En este ejemplo la radio.
2. En todos los lugares no se percibe la misma intensidad sonora, de manera que si nos
acercamos o alejamos lo oímos más o menos fuerte. En general puede decirse que un
campo es la región del espacio donde se manifiesta una propiedad física que toma un
valor distinto en cada punto.
3. Ya sabemos que la radio crea un campo de sonido, pero ¿cómo sabemos que en un
punto hay campo, hay sonido? Evidentemente la manera de saberlo es colocar a
alguien que no sea sordo o un micrófono. En general diremos que para probar la
existencia de un campo necesitamos un testigo o agente sensible al campo.
4. El testigo debe ser sensible al campo concreto, dicho de otra forma debe tener la
misma propiedad que el agente que crea el campo. Para probar la existencia de un
campo gravitatorio necesitamos una masa, para un campo eléctrico una carga, para
uno magnético una brújula que no es más que un imán.
5. En el caso de la radio, como comprenderá el sonido producido no llega a todos los
puntos de forma instantánea, sino que lo hará a la velocidad del sonido. En el caso de
los campos gravitatorio y eléctrico la perturbación se propaga a la velocidad de la luz.
6. Finalmente digamos que el campo creado por un agente no ejerce ninguna acción
sobre él mismo.
Clases de campos
Los campos se clasifican según que la magnitud física sea escalar o vectorial, así tenemos
campos escalares o vectoriales. Si la magnitud física, además de depender de la posición,
dependiera del tiempo al campo se le llama dinámico, y estático si no depende del tiempo.
A) Campos escalares: Son aquellos en los que la magnitud física que se manifiesta es un
escalar.
Por ejemplo, la densidad de un sólido no homogéneo, como la tierra, puede considerarse
como un campo escalar. Ya sabes que la densidad de la tierra aumenta si nos acercamos al
núcleo, es decir que depende de la posición: ρ=ρ(x,y,z).
Otro campo escalar es la temperatura en la atmósfera, porque en cada punto toma un valor, ya
que depende de la altitud, pero además en este caso se trata de un campo dinámico, porque
los valores en cada punto varían de unos días a otros es decir que T=T(x,y,z, t). .
Los campos suelen representarse por unas líneas (o también por superficies) obtenidas
uniendo todos los puntos en los que la propiedad física toma el mismo valor, por esa razón, en
los campos escalares, se las llama líneas equiescalares. En algunos casos estas líneas tienen
nombre propio, como en el caso de las temperaturas, donde se llaman isotermas, o de las
presiones, donde se llaman isóbaras.
B) Campos vectoriales: Son aquellos en los que la magnitud física que se manifiesta es un
vector. Los campos gravitatorio y eléctrico son de este tipo, porque en todo punto de los
mismos se puede definir una fuerza cuyo valor es función de la posición en el campo.
Lo que pasa es que para poner de manifiesto la existencia de esta fuerza es preciso colocar a
un testigo y resulta que el módulo de la fuerza no solo es función de la posición del punto,
sino que también depende de la característica del agente sensible o testigo.
Convención: En lo que sigue llamaremos M o Q a la masa o carga que crea el campo y m o q
a la masa o carga del testigo, aunque podrían llamarse m y m´
Suponga una masa M (o una carga eléctrica Q) en el origen de un SR. A su alrededor creará un
campo gravitatorio (o un campo eléctrico), de tal forma que si en cualquier punto del mismo
colocamos a un testigo m o q sobre él actuará una fuerza que viene dada por la ley de
gravitación de Newton en el caso de las masas o por la ley de Coulomb en el caso de las cargas.
r
m ⋅ m´ r
Fgrav = G 2 (− u r )
r
r
q ⋅ q´ r
Feléctr = k 2 u r
r
La dirección de la fuerza es siempre según la recta que une las cargas (o las masas), por tanto
tiene la misma dirección que el vector de posición de la m o q. En el caso de las masas el
r
sentido siempre es atractivo (en la misma dirección y sentido contrario a r , es decir en la
r
dirección y sentido de − u r ) y en el caso de las cargas depende de sus signos.
Resulta que la fuerza que actúa sobre el testigo depende de:
•
De la carga o masa que crea el campo (M o Q) y de la posición del punto P, es decir de
la distancia entre las cargas (r). Tanto una como otra son magnitudes propias del
campo.
• Además depende del valor de la masa o carga que hemos colocado como testigo (m o
q)
Para evitar que la fuerza en un punto de un campo dependa del testigo, vamos a definir una
magnitud nueva llamada Intensidad del campo de fuerzas como la fuerza por unidad de
testigo.
•
•
r
La intensidad del campo gravitatorio se representa por g y es la aceleración de la
gravedad, que conoces bien, y se mide en N/m o bien en m/s2.
r
La intensidad del campo eléctrico se representa por E y se mide en N/Coulomb
r
r F
E=
q
r
r F
g=
m
La Intensidad de campo gravitatorio es un vector en la dirección y sentido de la fuerza, ya que
las masas siempre son positivas. En el caso de la intensidad de campo eléctrico siempre tendrá
la misma dirección que la fuerza, pero el sentido dependerá del signo de q´ (recuerda el
producto de un escalar por un vector).
LÍNEAS DE FUERZA
El concepto de campo fue introducido por Faraday y a él se le ocurrió además una forma para
visualizarlo mediante unas líneas imaginarias, dibujadas de tal manera que sean en todo
momento tangentes al vector Intensidad de campo (o a la fuerza, que como sabemos tiene la
misma dirección). Para dibujarlas se siguen los pasos:
1. Coloca al testigo unidad en un
punto, ya que si m´=1Kg o
q´=+1C, fuerza e intensidad de
campo coinciden.
2. Sobre el testigo aparecerá
una fuerza en la dirección de
la recta que une los centros de
las masas o cargas
3. Si el testigo estuviera libre
se movería dibujando la línea
de campo y además nos dará
el sentido.
Además se sigue el criterio de dibujar más o menos líneas en función de que la intensidad de
campo sea grande o pequeña.
Siguiendo estos mismos pasos podemos dibujar las líneas de campo para una carga positiva o
negativa obteniendo:
En el caso de dos cargas (dipolo) o de dos masas se hace lo mismo, aunque teniendo en cuenta
que en cualquier punto del campo, la fuerza es debida a la suma vectorial que cada carga o
masa hace por separado sobre ella (es lo que más adelante veremos y que se llama principio
de superposición):
El resultado sería:
Propiedades de las líneas de fuerza:
1. Nos dan en todo momento la dirección y sentido de la Intensidad de campo
(precisamente para eso se dibujan)
2. Las líneas de fuerza del campo gravitatorio y del eléctrico no se cierran. Como puede
observarse en las figuras, las líneas de fuerza se inician en las cargas positivas y
terminan en las negativas, por eso a las cargas positivas se las llama fuentes y a las
negativas sumideros, así como las masas.
3. Las líneas de fuerza nunca se cortan. En efecto, ya que la intensidad de campo (y la
fuerza) es tangente a ellas en cada punto, si se cortaran entonces podríamos dibujar
dos tangentes y habría dos fuerzas distintas en el punto, lo que es absurdo.
LEY DE GRAVITACIÓN UNIVERSAL
Todas las masas en el universo, por el hecho de serlo, se atraen con una fuerza que es
proporcional al producto de las masas e inversamente proporcional al cuadrado de la
distancia que las separa (medida de centro a centro).
F=G
M⋅m
r2
La dirección de la fuerza que una masa ejerce sobre la otra es la de la recta que las une, así
que para un SR centrado en una de las masas la fuerza tiene la dirección del vector de
posición, pero el sentido puesto porque es atractiva. Por tanto vectorialmente sería:
r
M⋅m r
F = G 2 (− u r )
r
r
M⋅m r
F = −G 2 u r
r
•
r
u r es el vector unitario del vector de posición de la masa m respecto de M, es decir es
un vector unitario en la dirección de la línea que une los centros de las masas y el
sentido desde la masa que crea el campo hacia la otra.
•
El signo “menos” se interpreta como que son fuerzas atractivas, es decir que la fuerza
tiene la misma dirección y el sentido opuesto al vector de posición, es decir, la
r
dirección y sentido de − u r
•
G es una constante de proporcionalidad llamada “constante de gravitación universal”
(no debe confundirse con la aceleración de la gravedad, ya que son cosas
completamente distintas). Sus unidades se obtienen fácilmente despejándola de la
fórmula y su valor es:
G = 6,67 ⋅ 10 −11 N ⋅ m 2 / Kg 2
Características de la interacción gravitatoria: (e igual para la interacción ente cargas)
Las fuerzas gravitatorias son fuerzas centrales ya que al tener la fuerza la dirección de la recta
que une a las masas, siempre pasará por la masa que crea el campo, siendo este punto el centro
de fuerzas.
Las características de las fuerzas gravitatorias son las propias de las fuerzas centrales:
(Evidentemente el campo eléctrico, al igual que el campo gravitatorio, también es un campo
de fuerzas centrales y para él también podríamos decir todo lo que sigue).
1) Las fuerzas gravitatorias tienen simetría esférica porque el módulo de la fuerza de atracción
entre dos masas es igual en cualquier punto del espacio que se encuentre a la misma distancia
de la masa que crea el campo, y el lugar geométrico de esos puntos es una esfera con centro
en M y radio r.
2) Una partícula sometida a un campo de fuerzas centrales describe un movimiento en un plano.
En efecto, ya que el vector de posición de la masa m respecto de M, su velocidad y su aceleración
(fuerza) son siempre coplanarios y la partícula se moverá en el plano que determinan. (Los tres
vectores siempre forman un plano porque como la fuerza y el vector de posición siempre tienen la
r r
misma dirección, en realidad es como si solo fuesen dos vectores F y v .)
Un ejemplo sería el movimiento circular uniforme, en el que la fuerza a la que está sometida
la partícula (fuerza normal) apunta constantemente hacia el centro (por tanto es central) y
tiene la dirección del radio, igual que el vector de posición, de manera que esos dos vectores
con la velocidad siempre formarán un plano, es el del movimiento.
Precisamente esto justifica a la primera ley de Kepler, que dice que los planetas describen
órbitas elípticas planas en uno de cuyos focos está el sol.
r
3) El momento angular L de una partícula sometida a fuerzas centrales se conserva en el
r r
tiempo. En efecto, ya que como r y F tienen siempre la misma dirección, el momento de la
r
r r r
r dL
fuerza es nulo, porque M = r ∧ F = 0 . Y como por otro lado M =
al ser nulo el
dt
s
momento quiere decir que L = cte
r
Observa que si L es constante, también justifica que la trayectoria sea plana, ya que ello
quiere decir que no solo no variará ni en módulo ni en dirección, que como sabemos es la
r
perpendicular al plano del movimiento. Si L no cambia en dirección, el plano del movimiento
tampoco
4) El trabajo realizado por una fuerza central para llevar un cuerpo desde un punto A hasta
r r
otro B por una trayectoria circular es nulo. En efecto, ∫ F • d r = 0 porque en todo momento la
r
fuerza y el vector desplazamiento son perpendiculares (porque d r siempre es tangente a la
trayectoria y la fuerza, al ser central, siempre tiene la dirección del radio).
5) Las fuerzas centrales son fuerzas conservativas, por tanto, el trabajo para llevar a una masa
m desde un punto A hasta otro B es independiente del camino seguido y solo depende de la
posición de los puntos. (Es consecuencia del punto anterior, ya que una fuerza central
solamente realiza trabajo cuando mueve un cuerpo en dirección radial, mientras que el trabajo
es nulo cuando lo desplaza sobre la tangente).
Sea cual sea la trayectoria seguida siempre podremos
descomponerla en tramos infinitesimales verticales y
horizontales. En los tramos horizontales (2→3) el
r
r
trabajo es nulo porque F ⊥ d r . Solo hay trabajo en
los tramos 1→2 y 3→4
El trabajo que hace la fuerza gravitatoria para llevar
a la masa m desde al punto A hasta el B es el mismo
por el camino1 que por el camino2.
Al tratarse de un campo de fuerzas conservativas:
La energía que la masa m tiene en cada uno de los puntos del campo creado por M
solamente depende de la posición y por eso se le puede asignar una energía que
llamamos energía potencial.
Una partícula sometida a fuerzas conservativas conserva su energía mecánica:
Ec + Ep = cte
Observación: Es importante tener en cuenta que la fuerza actúa tanto sobre una masa como
sobre la otra y que son iguales y de sentidos opuestos (de acuerdo con la tercera ley de
Newton), es decir, una es la de acción y la otra de reacción:
r
r
F12 = − F21
F12 = F21
Lo que sucede es que solo nos interesa saber la fuerza que la masa que crea el campo ejerce
sobre el testigo, por ese motivo no prestamos atención a la que el testigo ejerce sobre la masa
que crea el campo, pero ello quiere decir que no exista.
Eso quiere decir que nosotros atraemos a la tierra exactamente con la misma fuerza que ella
nos atrae a nosotros. Te preguntarás porqué entonces la tierra no cae sobre los cuerpos y sí al
contrario. La respuesta es muy sencilla, y es que, la tierra tiene una masa muy grande
comparada con la nuestra, y por tanto presenta una inercia muy grande. Si la fuerza que ejerce
la tierra sobre nosotros es F12 y nuestra masa es m, nos atraerá con una aceleración que
vendrá dada por F12 = m ⋅ a . Por otro lado, nosotros ejercemos sobre la tierra una fuerza igual
en módulo F21 y si la masa de la tierra es M, la aceleración que nosotros ejercemos sobre ella
vendrá dada por F21 = M ⋅ a´ . Como ambas fuerzas son iguales, al ser M muy grande la
aceleración a´ con que la tierra se mueve hacia nosotros es prácticamente nula.
Ejemplo:
r 1s
Una partícula se encuentra en un campo de fuerzas del tipo F = u τ
r
r
Donde r es la distancia al origen O y u τ es un vector unitario perpendicular al radio
a) ¿Cuál es el lugar geométrico de todos los puntos en los que dicha fuerza tiene el mismo
módulo? ¿Tiene simetría esférica?
b) ¿Este campo de fuerzas es de tipo central?
c) Calcular el trabajo realizado por la fuerza a lo largo de una trayectoria cerrada. ¿Es un
campo conservativo?
a) Es evidente, que puesto que la fuerza solo depende de la distancia al origen O, la fuerza
tendrá el mismo valor en todos los puntos que estén a la misma distancia de O, por tanto el
lugar geométrico será una esfera con radio en O. En consecuencia el campo tiene simetría
esférica.
b) Como puede verse en la figura, al tener la fuerza la dirección de la tangente a la
circunferencia (perpendicular al radio dice el enunciado) no se trata de un campo de fuerzas
centrales porque la dirección de las fuerzas no concurre en un punto.
El campo sería central si el vector unitario en lugar de llevar la dirección de la tangente
r 1r
llevara la dirección del radio, es decir su fuera del tipo F = u r
r
c) Para calcular al trabajo a lo largo de una circunferencia como la de la figura:
•
como puede verse el vector desplazamiento y la fuerza siempre tienen la misma
dirección, así que forman 0º.
• el valor del módulo de la fuerza a lo largo de toda la circunferencia es constante, ya
que solo es función de r y valdrá F=1/R
• los límites de integración si queremos recorrer la circunferencia completa serán desde
0 hasta 2πR.
1
W = F ⋅ s ⋅ cos 0 = 2πR = 2π
R
Como el trabajo a lo largo de una trayectoria cerrada no es nulo, entonces la fuerza no es
conservativa.
Ejemplo:
Calcular la fuerza que la tierra ejercerá sobre un cuerpo de 1Kg de masa situado:
a) Sobre la superficie terrestre
b) a 100Km de la superficie
c) Comparar ambos resultados con los que se obtienen aplicando la fórmula P=mg
DATOS: Rt=6370Km Mt=5,98.1024Kg G=6,67.10−11Nm2/kg2
Como se sabe, a la fuerza con que la tierra atrae a los cuerpos se le llama peso, así que no es
más que la fuerza con que se atraen dos masas, pero cuando una de ellas es la tierra, por tanto,
aplicaremos la ley de gravitación universal:
F=G
M⋅m
r2
a) En el caso de que el cuerpo esté sobre la superficie de la tierra, la distancia que separa
ambos cuerpos es igual al radio de la tierra, porque se mide desde el centro de una masa al
centro de la otra, así que r=Rt
F=G
24
Mt ⋅ m
⋅1
−11 5,98 ⋅ 10
=
6
,
67
⋅
10
= 9,83New
2
Rt
6370.000 2
b) Cuando la masa está a 100Km de la superficie el problema es exactamente el mismo, solo
que ahora la distancia que separa las masas es r=Rt+h
F=G
Mt ⋅ m
5,98 ⋅ 10 24 ⋅ 1
−11
=
6
,
67
⋅
10
= 9,53New
(R t + h ) 2
(6370000 + 100000) 2
El resultado es perfectamente lógico, ya que como puede verse en la ley de gravitación
universal, a medida que aumenta r disminuirá F.
c) La fórmula P=mg es exactamente la misma que la de más arriba ya que, como veremos
enseguida, la aceleración de la gravedad es:
M
g = G 2t
r
Por tanto la misma expresión P=mg vale para ambos casos, simplemente lo que ocurre es que
la aceleración de la gravedad no vale igual en cada caso, porque, como puede verse depende
de r.
Lo que sucede es que cuando vemos la expresión P=mg inmediatamente pensamos en que
g=9,81m/s2 sin pararnos a pensar que la aceleración de la gravedad no es una constante
porque depende de la altura, incluso más adelante veremos que también depende de la latitud.
(Concretamente los pesos que hemos obtenido estarían calculados para el supuesto de que la
masa m estuviera en los polos.)
INTERACCIÓN DE UN CONJUNTO DE MASAS PUNTUALES. PRINCIPIO DE
SUPERPOSICIÓN
La ley de gravitación universal nos da la fuerza con que se atraen dos masas, pero no hace
referencia a la posible existencia de otras masas. Ello nos lleva al principio de superposición:
“Si una masa se encuentra en el campo creado por varias masas, la fuerza total sobre ella es la
fuerza resultante de las que cada masa, por separado, ejerza sobre ella.” De igual forma puede
decirse que el campo gravitatorio creado por varias masas en un punto es igual a la suma
vectorial de los campos que crean cada masa en ese punto.
r
r
Ftotal = ∑ Fi
r
r
Ftotal = m∑ g i
r
r
es decir que g total = ∑ g i
Ejemplo:
En los vértices de un cuadrado de 1m de lado hay tres masas de 1, 2 y 3 Kg. Calcular la fuerza
actuaría sobre una masa de 5Kg colocada en el cuarto vértice.
De acuerdo con el Principio de Superposición, la fuerza total sobre la masa de 5Kg es la
resultante de las fuerzas que cada masa por separado ejerce sobre ella.
Simplemente calculamos el módulo de las fuerzas de cada masa sobre la de 5Kg (la dirección
y sentido la dibujamos teniendo en cuenta que la fuerza siempre es atractiva y en la dirección
de la recta que une las masas y luego elegimos un sistema de referencia y las sumamos como
vectores que son.
m1 ⋅ m
1⋅ 5
= G 2 = 5G
2
r1
1
m ⋅m
2⋅5
F2 = G 2 2 = G
= 5G
r2
( 2)2
F1 = G
F3 = G
m3 ⋅ m
3⋅5
= G 2 = 15G
2
r3
1
En el sistema de referencia de la figura, la fuerza en forma de vector creada por cada masa
sobre la masa de 5Kg sería:
r
r
F1 = 5G j
r
r
r
F2 = −5G cos 45 i + 5Gsen 45 j
r
r
F3 = −15G i
r
r
r
F = −18,5G i + 8,5G j
El módulo sería F = (−18,5G ) 2 + (8,5G ) 2 = 20,35G = 1,36 ⋅ 10 −10 New
El ángulo con el eje X sería α = arctg
8,5G
= −24,67 º
− 18,5G
NOCIÓN DE CAMPO GRAVITATORIO: INTENSIDAD DE CAMPO
GRAVITATORIO DE UNA MASA PUNTUAL
Hemos visto que la fuerza que actúa sobre una masa m cuando la colocamos en un punto del
campo gravitatorio creado por otra masa M, depende de magnitudes propias del campo (la
masa que lo crea M y la posición del punto (r)) pero también depende del valor de la masa m.
Para evitar que la fuerza en un punto de un campo dependa de la masa del testigo, vamos a
definir una magnitud nueva llamada Intensidad del campo gravitatorio como la fuerza por
r
unidad de masa. La intensidad del campo gravitatorio se representa por g y es la aceleración
de la gravedad
r
r F
Mr
g = = −G 2 u r
m
r
• La Intensidad de campo gravitatorio solamente depende de la masa M que crea el
campo y de r, es decir de la posición del punto en el campo.
• La intensidad de campo en un punto nos permite conocer la fuerza que actuará sobre
r
r
un testigo de masa m colocado en ese punto: F = m g . Como se deduce de la relación,
la fuerza es un vector en la dirección y sentido de la fuerza, ya que las masas siempre
son positivas.
Por otro lado, hemos visto que el campo gravitatorio creado por varias masas en un punto es
r
r
igual a la suma vectorial de los campos que crean cada masa en ese punto. g total = ∑ g i es
decir se cumple el principio de superposición.
CAMPO GRAVITATORIO TERRESTRE
Suponiendo que la tierra es una esfera de radio R y de masa M, la fuerza con que atraerá a una
masa m colocada en sus inmediaciones vendrá dada por la ley de gravitación universal de
Newton:
r
M⋅m r
F = −G
ur
(R + h ) 2
r
r
A la fuerza con que la tierra a trae a las masas se le llama peso: F = mg , así que tenemos que
la aceleración de la gravedad en un punto no es más que la Intensidad de campo gravitatorio
en ese punto:
r
g = −G
r
M
ur
2
(R + h )
Para el caso concreto de puntos próximos a la superficie terrestre, y si despreciamos por ahora
la rotación de la tierra alrededor de su eje, su módulo sería:
g=G
24
M
−11 5,98 ⋅ 10
=
6
,
67
⋅
10
= 9,83m / s 2
R2
6370000 2
Factores que influyen en la aceleración de la gravedad
La aceleración de la gravedad no es una constante (a veces de tanto utilizar en los ejercicios
de mecánica el valor de 9,81 m/s2 algunos alumnos llegan a pensar que siempre vale eso) ya
que depende de la distancia entre las masas.
a) Variación de la gravedad con la distancia:
1. Disminuye con la altura sobre la superficie terrestre, ya que su módulo es:
g=G
M
M
=G
2
r
(R + h ) 2
Como puede verse, el valor de la aceleración de la gravedad
disminuye con el cuadrado de la distancia entre las masas.
M
= 9,81m s −2
R2
3. Disminuye linealmente en el interior de la Tierra. A primera vista podría pensarse que en
el interior de la Tierra la gravedad debería aumentar al disminuir r, pero no es así, ya que
solamente la masa encerrada en su interior contribuye al campo y, si te das cuenta, cada vez
que nos vamos adentrando en el interior de la tierra cada vez hay menos capas de masas que
influyen al campo, de manera que al disminuimos r también disminuimos la masa.
2. Tiene su valor máximo sobre la superficie de la Tierra: g T = G
Supondremos de que la densidad de la tierra sea constante.
Teniendo en cuenta que la densidad es ρ = m / V , para una esfera
4
de radio r tenemos que m = ρ ⋅ π r 3
3
La gravedad en el interior de la Tierra y en la superficie de la Tierra vienen dadas por:
g int
m
= G 2int = G
rint
4
ρ ⋅ π rint3
3
rint2
4
ρ ⋅ π R 3T
M
g T = G 2T = G 3 2
RT
RT
g int rint
=
gT R T
→
g int = g T
rint
RT
Resumiendo, el módulo de la aceleración de la gravedad vale:
g int = g T
r
RT
g fuera = G
M
r2
• Dentro de la tierra va aumentando linealmente con la distancia al centro. (es como una
recta de ecuación y=mx)
• En la superficie de la Tierra tiene el valor máximo gT
• Fuera de la Tierra disminuye con el cuadrado de la distancia
b) Variación de la gravedad con la latitud. En la superficie de la Tierra, la gravedad varía con
la latitud, debido al giro de la Tierra. Desde el punto de vista de un observador no inercial la
aceleración será la resultante de la gravedad en ese punto y de la aceleración centrífuga.
A 45º de latitud y al nivel del mar, la aceleración de la gravedad tiene el valor de 9,81 m/s2,
que es el valor que suele tomarse en los ejercicios de mecánica.
Ejemplo:
Encontrar la relación entre el valor de la gravedad en la superficie terrestre y el valor que tiene
a una altura h sobre la superficie.
Si llamemos g al valor en la superficie terrestre y g´ al valor que tiene a una altura h,
tendremos que:
M
g=G 2
R
g´= G
M
(R + h ) 2
g (R + h ) 2
=
g´
R2
⇒
g´= g
R2
(R + h ) 2
Como puede verse a medida que nos alejamos de la superficie terrestre el valor de g´
disminuye.
Ejemplo:
Calcular, en un lugar de la tierra situado a 45º de latitud:
a) la aceleración centrífuga
b) la aceleración de la gravedad
a) Hay que tener cuidado y darse cuenta de que la circunferencia que describe el punto de
latitud 45º no es igual al radio de la tierra, sino a r. Por tanto la fuerza centrífuga será:
v2
(ω r ) 2
Fc = m
=m
= m ω2 r
⇒
a c = ω2 r
r
r
como:
2π
2π
2π
• ω=
=
=
= 7,27 ⋅ 10 −5 rad / s
T 1día 24 ⋅ 3600
• r = R ⋅ cos 45 = 6370000 ⋅ cos 45 = 4504270m
Sustituyendo:
a c = ω 2 r = (7,27 ⋅ 10 −5 ) 2 ⋅ 4504270 = 0,024m / s 2
b) La aceleración de la gravedad en la superficie de la Tierra, suponiendo no girase, viene
dada por:
24
M
−11 5,98 ⋅ 10
g = G 2 = 6,67 ⋅ 10
= 9,83m / s 2
2
R
6370000
Ahora bien, al considerar su rotación, la aceleración real en un determinado lugar es la que
resulta de componer vectorialmente la aceleración centrífuga para ese punto con la
aceleración de la gravedad calculada anteriormente:
r
r r
g real = g + a c
Para un sistema de referencia como el de la figura, las aceleraciones en forma de vector
serían:
r
r
r
g = −9,83 cos 45 i − 9,83sen 45 j
r
r
a c = 0,024 i
r
r
r
g real = −6,927 i − 6,951 j
El módulo de la aceleración en ese punto sería:
g real = (−6,927) 2 + (−6,951) 2 = 9,81m / s 2
que es el valor que se toma para la aceleración de la gravedad en los ejercicios de mecánica.
Observa que, de acuerdo con lo anterior, el valor máximo para la aceleración de la gravedad la
tenemos en los polos, y el valor mas pequeño en el ecuador que es donde la aceleración centrífuga
es mayor. ( a c = ω 2 r para el ecuador r=Rt y además es un vector opuesto a g)
M
R2
M
= G 2 − ω2 R
R
g real,polo = G
g real,ecuad
Ejemplo:
¿Qué relación hay entre el peso de una masa m en las inmediaciones de la tierra y en un
planeta que tenga una masa 10 veces superior y el doble de radio?
Muy sencillo, expresamos la fuerza que cada planeta hace sobre la masa y las dividimos
miembro a miembro:
Ftierra = G
M⋅m
R2
Fplaneta = G
10M ⋅ m
( 2R ) 2
Ftierra
4
=
Fplaneta 10
⇒
Fplaneta = Ftierra
10
4
El resultado era de esperar ya que la fuerza de atracción gravitatoria (peso) es directamente
proporcional a la masa e inversamente proporcional al cuadrado de la distancia que separa las
masas, por tanto, será 10 veces mayor y 22 veces más pequeña.
Ejemplo:
En los vértices de un cuadrado de 1m de lado hay tres masas de 1, 2 y 3 Kg. Calcular la
intensidad de campo gravitatorio en el cuarto vértice. ¿Qué fuerza actuaría sobre una masa de
5Kg colocada allí? ¿Y sobre una masa de 6 Kg?
De acuerdo con el principio de superposición, el campo gravitatorio (g) creado por cada masa
por separado en el punto P es:
m
1
=G 2 =G
2
r1
1
m
2
g2 = G 2 = G
=G
r2
( 2)2
m
3
g 3 = G 2 = G 2 = 3G
r3
1
g1 = G
Ahora solamente queda sumar vectorialmente. En el sistema de referencia de la figura, la
intensidad de campo creada por cada masa sería:
r
r
g1 = G j
r
r
r
g 2 = −G cos 45 i + Gsen 45 j
r
r
g 3 = −3G i
r
r
r
g = −3,7Gi + 1,7Gj
El módulo sería g = (−3,7G ) 2 + (1,7G ) 2 = 4,07G = 2,71 ⋅ 10 −11 m / s 2
El ángulo con el eje X sería α = arctg
1,7G
= −24,67 º
− 3,7G
La fuerza sobre una masa colocada en el punto P se obtiene simplemente con la expresión
F=mg así que:
F5Kg = m 5 g = 5 ⋅ 2,71 ⋅ 10 −11 = 1,36 ⋅ 10 −10 New
F6 Kg = m 6 g = 6 ⋅ 2,71 ⋅ 10 −11 = 1,63 ⋅ 10 −10 New
Observación: Calcular el valor de la intensidad del campo gravitatorio en un punto (la
gravedad) tiene una ventaja enorme, ya que como vemos, una vez conocida, solamente hay
que multiplicar por la masa en el punto P y obtenemos la fuerza que actúa sobre ella. (bueno,
lo hemos hecho sobre su módulo, pero exactamente igual sería si hubiéramos multiplicado su
expresión vectorial). Sin embargo, si hubiéramos calculado la fuerza sobre la masa de 5Kg
sumando vectorialmente las fuerzas a partir de ese valor no podemos obtener la fuerza sobre
otra masa, como hemos hecho con la de 6Kg, y habríamos tenido que repetir el ejercicio y la
suma de vectores.
Esa es la razón por la que se define la intensidad de campo, porque su valor no depende de la
masa del testigo, sino de los agentes propios que crean el campo, es decir de las masas que lo
crean y de la posición.
ENERGIA POTENCIAL GRAVITATORIA DE UNA MASA EN PRESENCIA DE
OTRA
El campo gravitatorio es un campo de fuerzas centrales y por tanto conservativo, así que en él
puede definirse una energía potencial.
El trabajo que hace una fuerza conservativa para llevar un cuerpo desde un punto A hasta otro
B es independiente del camino seguido y solamente depende de la posición de los puntos A y
B. Por eso precisamente a esos puntos se le puede asociar una energía “que solamente
depende de la posición” y que llamamos energía potencial.
(Naturalmente, como es lógico, en un campo de fuerzas conservativo la energía potencial en un punto no
depende exclusivamente de la posición de ese punto, también depende de la masa que crea el campo" y de la
masa que hayamos colocado en ese punto". Precisamente para que tampoco dependa de la masa colocada en ese
punto definiremos más adelante el Potencial (V) como la energía potencial de una masa unidad.)
Por definición, “el trabajo que una fuerza conservativa hace para llevar un cuerpo desde un
punto A hasta otro B es igual a menos la variación de energía potencial entre esos puntos”:
WA →B,F.Conserv.Campo = − ∆Ep = Ep A − Ep B
Significado del signo menos: El signo menos indica que la fuerza conservativa del campo
hace trabajo espontáneo o real (trabajo positivo) cuando desplaza el cuerpo desde los puntos
de mayor energía potencial a los puntos con menor energía potencial. Dicho de otra forma,
bajo la acción de la fuerza conservativa un cuerpo se mueve espontáneamente desde los
puntos de mayor energía potencial a los puntos con menor energía potencial. (Observa que
WA →B,F.Conserv.Campo = + cuando EpA > EpB)
En un campo de fuerzas conservativas el trabajo que hacemos nosotros para llevar, contra las
fuerzas del campo y sin aceleración, un cuerpo desde un punto A hasta otro B no se pierde, sino
que queda acumulado en forma de energía potencial. Así podemos decir que “el trabajo que
hacemos nosotros para llevar un cuerpo desde un punto A hasta otro B, contra las fuerzas del
campo y sin aceleración, es igual a la variación de energía potencial entre esos puntos”
WA→B,nosotros = Ep B − Ep A = ∆Ep = − WA →B,F.Conserva .Campo
Ahora vamos a ver la expresión concreta de la energía potencial gravitatoria, para ello no hay
mas que calcular el trabajo que hace el campo gravitatorio para llevar una partícula desde el
punto A al B:
Br
r B
r B
M⋅m r
M⋅m
Ep A − Ep B = WA →B,campo = ∫ Fgrav • d r = ∫ − G 2 u r • d r = ∫ − G 2 ⋅ dr
r
r
A
A
A
r
donde hemos tenido en cuenta que vector unitario u r
r
y el vector desplazamiento d r tienen la misma
dirección y sentido, así que si que cos0=1. Teniendo
1
1
en cuenta además, que ∫ 2 dr = − nos quedaría
r
r
que:
B
WA→B,campo
1 1
 1
= −G ⋅ M ⋅ m −  = −G ⋅ M ⋅ m  −  = Ep A − Ep B
 rA
 rA rB 
Ep A − Ep B = −G
M⋅m
M⋅m
− −G
rA
rB
(Nota: aunque matemáticamente no es de lo más correcto escribir dos signos menos seguidos
y menos sin un paréntesis, pero lo escribiremos así porque resulta más didáctico. Además lo
pondremos en ese orden para que más adelante veas que estas expresiones son similares a las
del campo eléctrico)
Energía potencial gravitatoria en un punto. Como vemos, estrictamente solamente podemos
hablar de diferencia de energía potencial entre dos puntos (porque es el trabajo para llevar la
masa m desde uno a otro y por tanto debe haber dos puntos), pero si, por acuerdo, asignamos
cero a la energía potencial de uno de esos puntos, entonces podremos habar de energía
potencial absoluta (en realidad referida al punto que asignemos Ep=0).
Parece que lo razonable sería asignarle cero a la energía potencial en el infinito, porque como
la fuerza disminuye con el cuadrado de la distancia, en ese punto puede decirse que no hay
campo, por tanto, la diferencia de potencial entre un punto A y el infinito sería la energía
potencial en ese punto A.
Dicho de otra manera: La energía potencial de una masa m en un punto es igual al trabajo que
hace el campo para llevar a la masa m desde ese punto hasta el infinito. (Teniendo que cuenta
que nuestro trabajo y el que hace el campo son iguales y de signo contrario, podríamos decir
que la energía potencial de una masa m en un punto es igual a trabajo que tenemos que hacer
para traer a la masa, sin aceleración, desde el infinito hasta ese punto)
Ep A − Ep ∞ = −G
M⋅m
M⋅m
− −G
rA
∞
como 1 = 0
∞
Ep A = −G
M⋅m
rA
donde rA es la distancia que separa las dos masas. Como puedes ver la energía potencial en un
punto siempre es negativa y tiene su “máximo valor negativo” en la superficie terrestre y va
aumentando al alejarnos hasta llegar a cero en el infinito.
Particularización de la energía potencial para puntos próximos a la superficie terrestre:
En los puntos próximos a la superficie es razonable utilizar la conocida expresión:
∆Ep = Ep B − Ep A = mgh
Vamos a ver como se deduce esta expresión particular a partir de la general que hemos
obtenido:
Como puede verse en la figura
rA = Rtierra
rB − rA = h (Altura sobre la superficie terrestre)
Si llamamos M a la masa de la tierra y m a la masa del cuerpo, según hemos visto antes:
∆Ep = Ep B − Ep A = −G
r −r
M⋅m
M⋅m
− −G
= G⋅M⋅m B A
rB
rA
rA ⋅ rB
Teniendo en cuenta que:
• rB − rA = h
• al tratarse de puntos próximos a la superficie terrestre, prácticamente rB ≅ rA con lo
que podemos poner que rA ⋅ rB ≅ rA2 = R 2t .
• y recordando que el módulo de la Intensidad de campo, o gravedad viene dada por
M
g=G 2
Rt
al final nos quedaría que:
∆Ep = Ep B − Ep A = mgh
Cuestión:
De la expresión Ep=mgh, se deduce que la energía potencial es positiva y aumenta con la
altura. ¿Cómo es posible, si de la expresión Ep=–GMm/r se deduce que siempre es negativa y
aumenta con la altura?
La Ep que tiene una masa m en un punto del campo creado por otra M, como indica su
expresión general, siempre es negativa y su valor máximo es cero, que corresponde a la Ep en
el infinito. Lo que pasa es que siempre medimos “diferencias” de energía potencial y cuando
restamos obtenemos el mismo valor con independencia de donde tomemos el cero. Por tanto
entre dos puntos cualquiera hay la misma ∆Ep si el nivel cero lo tomamos en el infinito (que
es lo natural) como si lo ponemos en cualquier otro lugar como la superficie de la tierra o
donde sea:
Fíjate que, independientemente de donde tomemos el cero de Ep, el ∆Ep entre dos puntos
siempre vale igual: EpB ‒ EpA = 20 J. Es exactamente el mismo caso que si montamos a un
niño sobre una mesa para medir su altura. Tanto si lo medimos de pies a cabeza, como si
medimos desde el suelo a la cabeza y restamos la distancia del suelo a los pies obtendremos lo
mismo. “No importa que al cambiar de sistema de referencia en cada medida tengamos
valores distintos, lo que importa que es la diferencia siempre tendrá el mismo valor”.
Energía potencial “de una masa” debida al campo creado por una asociación de masas:
de acuerdo con el principio de superposición la energía potencial que tendrá es la debida al
campo que independientemente cada masa crea sobre ella, así que:
Ep = −G
m1 ⋅ m
m ⋅m
m ⋅m
m
−G 2
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ −G n
= −Gm ∑ in=1 i
r1
r2
rn
ri
Energía potencial de una asociación de masas: En este caso la energía potencial debida a
todas ellas se obtiene sumando la energía potencial de todos los pares de masas. Por ejemplo
la energía potencial de la asociación de la figura sería:
m m
mm
m m 
Ep = −G  1 2 + 1 3 + 2 3 
r13
r23 
 r12
Ep = −G ∑
mi m j
rij
Ejemplo:
Imagina que hay dos masas m1=10Kg y m2=20Kg como se indica en la figura. Calcular el trabajo que
hemos de hacer para llevar una masa m de 5Kg desde la posición A(4,0) hasta la B(8,0)
Como sabemos el trabajo que hacemos nosotros es igual al incremento de energía potencial, así
que solamente tenemos que calcular la Ep que la masa m tiene al final y al principio y restarlas.
WA→B,nosotros = ∆Ep = Ep B − Ep A = − WA →B,F.Conservat .
De acuerdo al principio de superposición, la Ep que la masa m tiene en el punto A es debida a
la que tiene como consecuencia del campo que crea m1 mas la debida al campo que crea la
masa m2, es decir:
m ⋅m
m ⋅m
 10 10 
Ep A = −G 1
+ −G 2
= −Gm +  = −32,5G
r1A
r2 A
4 5
De igual forma, la Ep cuando está en el punto B será:
m ⋅m
m ⋅m
 10 10 
+ −G 2
= −Gm +
Ep B = −G 1
 = −17,96G
r1B
r2 B
 8 8,54 
Por tanto:
WA →B,nosotros = Ep B − Ep A = −32,5G − (−17,96G ) = +15,54G
POTENCIAL GRAVITATORIO
Recuerda que la fuerza que actúa sobre una masa m, en un punto de un campo creado por otra
masa M, depende del valor de m. Para evitar ese inconveniente se definió la intensidad de
campo como fuerza por unidad de masa.
Lo mismo le ocurre a la variación de energía potencial de una masa m entre dos puntos A y B,
de un campo creado por otra masa M, que también depende del valor de m. Para evitar ese
inconveniente vamos a definir una magnitud nueva como variación de energía potencial por
unidad de masa y que llamaremos variación Potencial (V):
B
Ep A − Ep B WA→ B,F.Conserv
VA − VB =
=
=
m
m
r
r
F
•
d
r
F
.
Conserv
∫
A
m
B
r r
= ∫ g • dr
A
B
r r B
r B
Mr
M
VA − VB = ∫ g • d r = ∫ − G 2 u r • d r = ∫ − G 2 ⋅ dr
r
r
A
A
A
r
donde hemos tenido en cuenta que vector unitario u r y
r
el vector desplazamiento dr tienen la misma dirección
y sentido, así que si que cos0=1. Teniendo en cuenta
1
1
además, que ∫ 2 dr = − nos quedaría que:
r
r
B
1 1
 1
VA − VB = −G M ⋅ −  = −G M ⋅  − 
 r A
 rA rB 
VA − VB = −G
M
M
− −G
rA
rB
Obviamente llegaremos al mismo resultado si dividimos la deferencia de energía potencial
por el testigo m ya que, como hemos dicho, la ddp entre dos puntos se definie como la
diferencia de Energía potencial que tiene entre esos puntos un testigo unidad:
VA − VB =
Ep A − Ep B
M
M
= −G
− −G
m
rA
rB
Potencial gravitatorio en un punto. Como sabemos estrictamente solamente podemos hablar
de ddp entre dos puntos (porque se ha definido como el trabajo pare llevar a la unidad de
masa entre esos dos puntos). No obstante si, por acuerdo, asignamos cero al potencial de uno
de esos punts, entonces podremos habar de potencial absoluto en un punto. El punto que se
elige es el infinito porque allí se supone que ya no hay campo.
WA→B,F.Conservat
podemos decir que:
Dicho de otra manera, teniendo en cuenta que VA − VB =
c
El potencial en un punto A es igual al trabajo que hace el campo para llevar una masa de 1Kg
desde ese punto hasta el infinito. (Teniendo que cuenta que nuestro trabajo y el que hace el
campo son iguales y de signo contrario, podríamos decir que el potencial en un punto A es
igual al trabajo que tenemos que hacer para traer una masa de 1Kg desde el infinito hasta ese
punto).
M
M
− −G
VA − V∞ = −G
rA
∞
como 1 = 0
∞
M
VA = −G
rA
donde rA es la distancia que separa la masa que crea el campo del punto A.
Ejemplo:
Calcular el potencial gravitatorio creado por una esfera de 100Kg de masa y dos metros de
diámetro en un punto situado a 9m de su superficie. ¿Cuál será la energía potencial de una
masa de 1Kg situada en dicho punto?
Suponiendo que la esfera es homogénea
podemos considerarla como una masa puntual
concentrada en su centro.
a) Como hemos visto la ddp entre el punto A y el infinito será igual al potencial en el punto A,
que vale:
VA = −G
M
6,67 ⋅ 10 −11 ⋅ 100
=−
= −6,67 ⋅ 10 −10 J / Kg
rA
10
b) De acuerdo con su definición, la energía potencial de una masa unidad en un punto y el
potencial en ese punto son exactamente la misma cosa, así que Ep A = −6,67 ⋅ 10 −10 Julios
Para otro valor cualquiera de m´ la relación entre ambas magnitudes sería:
Ep A = m´⋅VA
RELACION ENTRE CAMPO Y POTENCIAL
r
Si te das cuenta el campo ( g ) es un vector y el potencial (V) es un escalar, así que su correcta
relación es a través de un operador vectorial llamado gradiente, pero eso escapa de la programación
de bachillerato, así que nos limitaremos a relacionar el módulo del campo y el potencial.
Caso particular de campo uniforme, es decir, de puntos cercanos en los que la gravedad puede
considerarse constante, entonces, teniendo en cuenta la definición de ddp,
B
r r
VA − VB = ∫ g • d r = g r
B
A
= g (rB − rA ) = g ⋅ d
A
Dice que la ddp entre dos puntos, entre los que
puede considerarse constante el valor del
campo, es igual al valor del campo por la
distancia entre esos puntos. A la misma
conclusión llegaríamos restando el potencial
en el punto A del que tiene en B:
VA − VB = −G
M (rB − rA )
M (rB − rA )
M
M
− −G
=G
≅G
= g(rB − rA ) = g ⋅ d
rA
rB
rA rB
rA2
r
La relación referida a un punto concreto, teniendo en cuenta las expresiones del módulo de g
y la del potencial V en un punto:
VA = −G
M
M r
= −G ⋅ A = − g A .rA
rA
rA rA
Quiere decir que: si multiplicamos el módulo del campo en un punto A por la distancia del
punto a la masa que crea el campo al punto se obtiene el potencial en ese punto.
Hay un detalle importante:
•
•
r
Si en un punto de un campo conocemos el valor de la Intensidad de campo ( g o
r
E ) podremos presumir exactamente lo que ocurrirá cuando coloquemos una masa m o
a una carga q en un punto cualquiera (podremos calcular exactamente el módulo de la
r
r
r
r
fuerza que actuará, su dirección y sentido, ya que F = mg o bien F = qE )
Sin embargo, si en un punto del campo solo conocemos el potencial en ese punto no
podremos predecir lo que ocurrirá. Cosa distinta sería si conocemos el potencial en
dos puntos, entonces sí, porque, tanto la masa como la carga se moverán hacia donde
disminuya su energía potencial.
SUPERFICIES EQUIPOTENCIALES
Como su propio nombre indica (equi significa igual) una superficie equipotencial es aquella
en la que en todos sus puntos hay el mismo potencial. Dibujemos una superficie y
supongamos que es equipotencial:
Propiedades de las superficies equipotenciales:
1. Las superficies equipotenciales son siempre perpendiculares al vector intensidad de campo.
En efecto, ya que para desplazamos de un punto a otro de la superficie es necesario que el
r
vector desplazamiento d r sea coplanario con la superficie, y puesto que según la definición
de ddp entre dos puntos:
B
r r
VA − VB = ∫ g • d r
A
r
r
si la superficie es equipotencial VA−VB=0 lo que quiere decir que: g = 0 o que d r = 0 ambas
cosas son absurdas porque si no hay campo o no hay desplazamiento no habría problema, así
que la única otra alternativa es que el producto escalar de ambos vectores sea nulo, es decir
que formen ángulo de 90º.
2. El trabajo para lleva una masa de un punto A de una superficie equipotencial a otro B de la
misma superficie equipotencial es cero. Obvio, ya que WA →B,F.Conservat = m (VA − VB ) y al
r r
movernos por la misma superficie equipotencial VA=VB. Además es cero porque como g y F
r
r
tienen la misma dirección, entonces F ⊥ d r .
3. Para el caso de una masa, o de una carga las superficies equipotenciales son esferas
concéntricas. En efecto, ya que como las líneas de campo son radiales, para que las superficies
sean normales a ellas deben ser esferas con centro en la masa o carga que crea el campo.
4. Dos superficies equipotenciales nunca pueden cortarse porque ello implicaría que en los
puntos de corte podríamos trazar dos perpendiculares y, como ya vimos, las líneas de campo
no se cortan. Además, imagina que dos superficies equipotenciales se cortaran, entonces en
ambas habría el mismo potencial y por tanto sería la misma superficie.
Ejemplo:
Imagina tres puntos 1, 2 y 3 en los que el potencial gravitatorio va disminuyendo, es decir que
V1>V2>V3. ¿ Hacia donde se movería una masa m si la colocamos en el punto 2 y la dejamos
libre?
La masa m (o una carga independientemente del signo) se mueve espontáneamente hacia el
punto en el que disminuya su energía potencial. (Recuerda que eso precisamente es lo que
indica el signo menos de la definición WA→B,F.Conserv.Campo = −∆Ep = Ep A − Ep B )
Como Ep=m.V y teniendo en cuenta que las masas siempre son positivas (cosa que no ocurre
con las cargas) es obvio que Ep1>Ep2>Ep3 y en consecuencia las masas se mueven siempre de
forma espontáneamente hacia potenciales decrecientes. En este caso hacia V3.
Si se tratara de una carga, como Ep=q.V resulta que si la carga es positiva se movería hacia
potenciales decrecientes, pero si fuese una carga negativa se movería hacia donde aumente el
potencial.
Ahora que sabemos hacia donde se moverá la masa
r
podremos dibujar el vector campo g pero no podríamos si
solamente conociéramos el potencial en un punto.
Ejemplo:
Entre dos puntos A y B de un campo eléctrico existe una diferencia de potencial de 100
voltios. ¿Qué trabajo realiza el campo para llevar una carga positiva de 2µC desde A hasta B?
Al tratarse de un campo eléctrico, la característica del campo es la carga eléctrica, por tanto
podemos poner que:
WA →B,campo = q (VA − VB )
sustituyendo
WA→B,campo = 2 ⋅ 10 −6 ⋅ 100 = 2 ⋅ 10 −4 Julios
Como puede verse el Potencial se mide en Julios/Coulombio que recibe el nombre especial de
Voltio. De manera análoga el Potencial gravitatorio se mide en Julios/Kg que no tiene un
nombre especial.
Si en lugar de preguntarnos por el trabajo del campo, nos hubiesen preguntado ¿qué trabajo
hacemos nosotros para llevar la carga de 2µC desde A hasta B? La respuesta, obviamente,
sería –2.10−4J
LEYES DE KEPLER
1. Los planetas describen órbitas elípticas planas, en uno de cuyos focos está el sol.
Esta ley resulta evidente si tenemos en cuenta que las fuerzas gravitatorias son fuerzas
centrales y que, por tanto, se conserva el momento angular. Al ser constante el momento
r r
r
r
angular L = r ∧ mv (tanto en módulo como en dirección) el plano formado por los vectores r
v
y v también debe permanecer constante.
2. El radio vector que une el sol con uno de los planetas barre áreas iguales en tiempos
iguales. Dicho de otra forma, la velocidad con la que el vector de posición del planeta
respecto al sol barre áreas es constante.
En la figura hemos representado el área barrida por el vector de posición en el tiempo ∆t .
Como recordarás, el módulo del producto vectorial de dos vectores es igual al área del
paralelogramo que forman, y obviamente la mitad al triángulo. Y teniendo en cuenta que la
r
r
velocidad es v = d r / dt
dA =
r
1r r 1r r
1 s
1 r
r ∧ d r = r ∧ v dt =
r ∧ mv dt =
L dt
2
2
2m
2m
dA
1 r
=
L = cte.
dt 2m
3. Los cuadrados de los periodos de revolución de los planetas son proporcionales a los cubos
de la distancia media de los planetas al sol: T2 = kR3
La demostración de la tercera ley es consecuencia de la ley de gravitación universal de
Newton. Que el planeta se mantenga en órbita supone, desde el punto de vista de un
observador no inercial, que el peso del satélite se compense con la fuerza centrífuga:
Peso = Fc
⇒
G
M⋅m
v2
=
m
r
r2
Teniendo en cuenta la relación entre la velocidad lineal y angular del planeta es v = ω ⋅ r y
que ω = 2π / T
G
M⋅m
v2
4 π2 2
2 2
=
m
=
ω
r
=
r
r
r2
T2
despejando el periodo:
T2 =
4π 2 3
r
GM
T2 = k ⋅ r3
Como puede verse todo lo que engloba el círculo son constantes (no aparece la masa del
planeta) y el resultado de la operación, lógicamente, corresponde a una constante
SATÉLITES: VELOCIDAD ORBITAL Y VELOCIDAD DE ESCAPE
Velocidad orbital: Para que un satélite de masa m orbite a una distancia r alrededor de la
tierra, desde el punto de vista de un observador no inercial, es preciso que la fuerza peso con
que lo atrae la tierra sea igual a la fuerza centrífuga:
Fgrav = Fc
G
M⋅m
v2
m
=
r
r2
v orbital =
GM
r
Órbita geoestacionaria: Como vemos la velocidad orbital del satélite no depende de su masa,
solamente depende del radio de la órbita y viceversa. Por tato, habrá un radio para el que el
satélite tenga la misma velocidad angular que la Tierra (a esa órbita se le llama
geoestacionaria)
Los satélites geoestacionarios, como
los de comunicaciones, son los que se
encuentran en todo momento sobre el
mismo punto, dicho de otra forman
giran con la misma velocidad angular
que la tierra (ω=2π/1día). Su órbita,
además, debe estar en el plano del
ecuador.
Simplemente se trata de poner el radio de la órbita en función del periodo, “que debe ser 1
día”, para gire con la misma velocidad angular de la tierra. Para un SRNI, la fuerza de
atracción gravitatoria debe compensarse por la centrífuga, así que: (es como deducir la tercera
ley de Kepler, pero ahora despejamos el radio)
M⋅m
v2
4 π2 2
2 2
G 2 =m
= ω r = 2 r
r
r
T
despejando el radio de la órbita, y sustituyendo T=1día:
r=
3
GM ⋅ T 2 3 6,67 ⋅ 10 −11 ⋅ 5,98 ⋅ 10 24 ⋅ (24 * 3600) 2
=
= 42259Km
4π 2
4π 2
La energía total del satélite cuando está en su órbita a una distancia r del centro de la tierra
será suma de cinética y potencial, es decir:
E = Ec + Ep
E=
1
M⋅m

2
mv orb
+ − G

2
r 

2
1  GM  
M⋅m
 + − G
E = m


2 
r  
r 
1 M⋅m
E=− G
2
r
•
Mientras el satélite permanezca en esa órbita no consume energía, porque se desplaza
por una superficie equipotencial. Recuerda que:
WA →B,campo = m (VA − VB )
Si VA=VB ⇒ W=0
además en el caso del campo gravitatorio resulta obvio, ya que la fuerza gravitatoria y el
vector desplazamiento por una superficie equipotencial (que son esferas concéntricas)
forman ángulo de 90º y su coseno es 0
•
El signo menos de la energía total del satélite indica que se trata de un sistema ligado a
la tierra, es decir que por sí mismo nunca se podría escapar de la atracción terrestre.
Para escapar debería tener energía positiva o como mínimo nula.
La energía necesaria para poner un satélite en órbita: Esta energía es positiva porque debemos
hacerla nosotros. Supongamos que inicialmente el satélite está en reposo sobre el suelo. Para
que empiece a subir tenemos que ejercer un trabajo sobre él (WF.NoConserv) y en consecuencia
no se conserva la energía mecánica, por tanto: ∆Ec + ∆Ep = WA→B
F. NoConservat
Ec suelo + Ep suelo + WA→ B
= Ec B + Ep B
F. NoConservat
−G
M⋅m
1
M⋅m
2
+ WA →B
= mv orbital
−G
RT
2
r
F. NoConservat
2
WA→B
F. NoConservat
WA→B
F. NoConservat
1  GM 
M⋅m
M⋅m
 −G
= m
+G

2  r 
r
RT
 2r − R T 

= GMm
2
R
r

T

Ese trabajo se lo comunicamos en forma de energía cinética: WF.NoConserv. = 12 mv o2
Por eso solemos decir: “se lanza un cuerpo con una velocidad inicial vo …”.
Si balanceamos entre cuando el satélite está en el suelo y ya le hemos comunicado esa energía
y cuando está arriba orbitando, ahora ya sí que se conserva la energía mecánica, puesto que
ahora la única fuerza es la gravitatoria, que es conservativa: ∆Ec + ∆Ep = 0
1
mv o2 = WA→ B
2
F. NoConservat
Como ves, ambos razonamientos son idénticos aunque parezcan distintos.
Ec suelo + Ep suelo = Ec B + Ep B
donde Ec suelo =
La velocidad de escape de un cuerpo que es lanzado desde la superficie de la tierra es aquella
que permite que el cuerpo escape de la atracción terrestre y ello requiere que su energía total
sea positiva o nula como mínimo.
En efecto, ya que como sabemos, cuando lanzamos un cuerpo desde la superficie de la tierra,
la atracción gravitatoria hace que su velocidad vaya disminuyendo conforme se aleja a la vez
que se va transformando en potencial.
•
•
Si queremos que el cuerpo escape completamente debemos comunicarle una energía
cinética de manera que no se detenga hasta llegar al infinito.
Y en el infinito su energía mecánica sería cero porque llega con velocidad cero y
porque allí su Ep=0, ya que es inversa a la distancia, así que como la energía mecánica
en el lanzamiento debe ser igual a la que tiene en el infinito:
Ec tierra + Ep tierra = Ec ∞ + Ep ∞
E=
1
M⋅m 1
M⋅m


2
2
mv escape
+ − G
 = mv ∞ +  − G

∞ 
2
R  2


de donde:
v escape =
2GM
R
•
Si el cuerpo estuviera a una altura h la velocidad de escape, sería v escape =
donde r=R+h
•
Como puedes ver comparando la velocidad orbital y la velocidad de escape:
v escape = 2 ⋅ v orbital
2 GM
r
Ejemplo:
Imagina un planeta que tuviese una masa igual a 3.1015 Kg y un radio de 1000 Km. Calcula:
a) La energía potencial, cinética y total de un satélite de 500 Kg cuando está en la superficie
de ese planeta a punto de lanzarse al espacio.
b) La energía potencial, cinética y total del satélite cuando esté orbitando a 250 Km sobre la
superficie del planeta.
c) Qué energía hemos debido aportar al satélite para ponerlo en esa órbita.
d) Velocidad para que escape de la atracción del campo gravitatorio
e) La energía adicional que hemos de aportarle para que escape del campo gravitatorio
Datos: G=6,67.10−11 N m2 Kg−2
a) Cuando está en reposo sobre la superficie del planeta solamente tiene energía potencial, que
además es donde tiene el valor más pequeño (el máximo negativo).
Ep SupPlaneta = −G
Ec SupPlaneta =
M⋅m
3 ⋅ 1015 ⋅ 500
= −6,67 ⋅ 10 −11
= −100 Julios
R
1000000
1
mv 2 = 0
2
E Órbita = Ec + Ep = −100 Julios
b) Cuando el satélite está a una altura h sobre la superficie del planeta tiene una energía
potencial (que es independiente de si está girando o no):
Ep SupOrbita = −G
M⋅m
3 ⋅ 1015 ⋅ 500
= −6,67 ⋅ 10 −11
= −80 Julios
r
1000000 + 250000
fíjate que la energía potencial a una altura h es mayor que la que tenía en la superficie de la
tierra. Es un número negativo que va creciendo con la altura hasta alcanzar su valor máximo
igual a cero en el infinito.
Si subimos el satélite hasta esa altura y no hacemos nada más el satélite nos caería encima
exactamente igual que cuando se lanza una piedra hacia arriba. Si pretendemos que el satélite
orbite ahora debemos comunicarle una velocidad tangencialmente (igual a la velocidad
orbital) de forma que (desde el punto de vista de un observador no inercial) la fuerza
centrífuga compense el peso de satélite:
Fgrav = Fc ⇒ G
M⋅m
v2
m
=
⇒ v orbital =
r
r2
GM
6,67 ⋅ 10 −11 ⋅ 3 ⋅ 1015
=
= 0,4 m / s
r
1000000 + 250000
La energía cinética que tendrá en la órbita es:
2
Ec Órbita
1
1  GM 
1 M⋅m
 = G
= mv 2 = m
= 40 m / s

2
2 
r 
2
r
E Órbita = Ec + Ep = +40 − 80 = −40 Julios
Observa la relación que guardan las distintas energías entre sí. Precisamente se han escogido
estos valores para obtener números sencillos que ayuden a ver claramente esas relaciones que
son las mismas con independencia de los datos.
c) La energía que hemos de aportarle para ponerlo en órbita es:
1. la energía necesaria para subirlo hasta la altura h, que será igual a la variación de
energía potencial ∆Ep = WA →B
= −80 − (−100) = 20 Julios . Como ya indicamos,
F. NoConservat
ese trabajo que hemos de hacer es el mismo que si subimos una piedra hasta un tejado,
con la única diferencia de que al ser h muy grande la gravedad no puede considerarse
constante y no podemos utilizar la expresión particular ∆Ep = mgh sino que hemos
utilizado su expresión general.
2. la energía necesaria para que orbite con la velocidad orbital, es decir 40 Julios
Por tanto la energía necesaria para ponerlo en órbita será 60 Julios.
A la misma conclusión se llegaría aplicando el principio de conservación de la energía entre la
superficie del planeta y la órbita:
∆Ep + ∆Ec = WA→B
F. NoConservat
WA→B
F. NoConservat
WA→B
= (Ep Órbita − Ep Sup.Planeta ) + (Ec Órbita − Ec Sup.Planeta )
= (−80 − (−100)) + (40 − 0) = +60 J
F. NoConservat
d) La velocidad de escape es la velocidad que hemos de comunicarle para mandarlo al infinito con
velocidad cero y donde la energía potencial también es cero y por tanto la energía total en el infinito
es cero. Fíjate que conforme sube su velocidad disminuye y también su energía cinética hasta hacerse
nula, mientras que la potencial va aumentando (se hace un número negativo cada vez menor) hasta
llegar a su valor máximo igual a cero.
Ec B + Ep B =
1
M⋅m
2
mv escape
−G
=0
2
r
2GM
2 ⋅ 6,67 ⋅ 10 −11 ⋅ 3 ⋅ 1015
=
= 0,566 m / s
r
1000000 + 250000
e) La energía necesaria para que escape del campo gravitatorio es la energía para mandarlo
hasta el infinito, donde la Ec=0 y la Ep=0, así que aplicando la conservación de la energía
entre el punto B y el infinito:
v escape =
∆Ep + ∆Ec = Wb→∞
F. NoConservat
WA→B
F. NoConservat
WA→B
= (Ep ∞ − Ep Órbita ) + (Ec ∞ − Ec Órbita )
= (0 − (−80)) + (0 − 40) = +40 J
F. NoConservat
fíjate que
• la energía para mandar el satélite al infinito coincide con la energía total que tiene,
pero cambiada de signo.
• la energía para mandarlo al infinito no es la energía cinética que corresponde a la
velocidad de escape, (esta sería ½.500.0,5662=80J). Esta energía sería la necesaria para
que escapase si estuviese parado a esa altura (Ep=−80J), pero es que como está
orbitando además de la potencial tiene una energía cinética adicional de +40J, por eso
solamente hemos de aportar 80J−40J que ya tiene = 40J
• el resultado está de acuerdo con lo que habría sido necesario para mandarlo al infinito
desde la superficie de la tierra. Allí tenía una energía total de −100 J, así que el trabajo
necesario para mandarlo al infinito sería de +100J.
En el caso que nos ocupa hemos invertido +60J en ponerlo a orbitar y luego +40J en
mandarlo al infinito, en total +100J.
Ejemplo:
Un satélite de 100Kg de masa describe una orbita circular a 200Km de la superficie terrestre.
a) Energía potencial del satélite cuando está en la superficie de la tierra.
b) Calcular su velocidad orbital
b) Energía potencial, cinética y total del satélite
c) ¿Qué le pasaría al radio de la órbita si por efecto del rozamiento el satélite va perdiendo
energía? Y en particular ¿Qué le ocurriría a su velocidad angular?
d) Periodo
e) Energía necesaria para ponerlo en órbita
f) Velocidad necesaria para que escape del campo gravitatorio
g) Energía necesaria para que escape del campo gravitatorio.
Datos: MT=5,98.1024Kg
a) Ep Sup .Tierra = −G
G=6,67.10−11 N m2 Kg−2
RT=6370Km
M⋅m
5,98 ⋅ 10 24 ⋅ 100
= −6,67 ⋅ 10 −11
= −6,26 ⋅ 10 9 Julios
r
6370000
b) Para un observador situado en el satélite, éste estará
sometido a dos fuerzas en la misma dirección y sentido
contrario: El peso y la F.centrífuga, y ambas deben ser
iguales para que se mantenga en órbita.
r = R Tierra + h
Fgrav = Fc
de donde:
⇒
G
M⋅m
v2
=
m
r
r2
v orbital =
GM
=
r
GM
=
R+h
6,67 ⋅ 10 −11 ⋅ 5,98 ⋅ 10 24
= 7792m / s
6370000 + 200000
b) La energía potencial, cinética y total serían:
Ep Órbita = −G
M⋅m
5,98 ⋅ 10 24 ⋅ 100
= −6,67 ⋅ 10 −11
= −6,07 ⋅ 10 9 Julios
r
6370000 + 200000
2
Ec Órbita
1
1  GM 
1 M⋅m
 = G
= mv 2 = m
= 3,04 ⋅ 10 9 m / s

2
2 
r 
2
r
E Órbita = Ec + Ep = 3,04 ⋅ 10 9 + (−6,07 ⋅ 10 9 ) = −3,04 ⋅ 10 9 Julios
O bien
E Órbita =
1
M⋅m
1 M⋅m

mv 2 +  − G
= −3,04 ⋅ 10 9 Julios
=− G
2
r
2
r


1 M⋅m
c) Teniendo en cuenta que la energía total es E = − G
resulta que, puesto que es negativa,
2
r
disminuirá siempre que aumente en valor absoluto, es decir cuando disminuya el radio. Así pues,
cuando por efecto del rozamiento pierda energía comenzará a describir una espiral de radio cada
vez menor hasta caer en la tierra, o lo que es igual, la altura h cada vez será menor y como:
GM
v orbital =
R+h
al disminuir h, su velocidad lineal aumentará, y lo mismo le sucederá a la velocidad angular,
ya que:
v
GM
ω= =
r
(R + h ) 3
al disminuir h, la velocidad angular aumenta con mayor rapidez que la lineal.
d) El periodo
M⋅m
v2
4π 2 2
4π 2 r 3
4π 2 (6570000) 3
2
=
m
=
(
ω
r
)
=
r
⇒
T
=
=
= 5298seg
r
GM
6,67 ⋅10 −11 ⋅ 5,98 ⋅10 24
r2
T2
o bien teniendo en cuenta que:
v 2π
2π r 2 ⋅ π ⋅ 6570000
ω= =
⇒
T=
=
= 5298seg
r
T
v
7792
G
e) La energía que hemos de comunicarle nosotros para ponerlo en órbita será la necesaria para
subirlo hasta esa altura (∆Ep) más la energía cinética que luego hay que comunicarle
tangencialmente para que comience a orbitar. Aplicando el principio de conservación de la
energía entre la superficie de la tierra y la órbita:
∆Ep + ∆Ec = WA→B
F. NoConservat
WA→B
F. NoConservat
= (Ep Órbita − Ep Sup.Tierra ) + (Ec Órbita − Ec Sup .Tierra )
= (−6,07 ⋅ 10 9 − (−6,26 ⋅ 10 9 )) + (3,04 ⋅ 10 9 − 0) = +3,23 ⋅ 10 9 J
WA→B
F. NoConservat
f) La velocidad de escape es la velocidad que hemos de comunicarle para mandarlo al infinito,
donde la energía es cero, así que:
Ec A + Ep A =
v escape =
2GM
=
r
1
M⋅m
2
mv escape
−G
=0
2
r
2 ⋅ 6,67 ⋅ 10 −11 ⋅ 5,98 ⋅ 10 24
= 11019m / s
6370000 + 200000
FORMAS DE LA TRAYECTORIA DEL LANZAMIENTO DE UN COHETE
En primer lugar vamos a recordar que:
•
•
•
La energía potencial gravitatoria siempre es negativa y que va aumentando conforme
nos alejamos de la superficie de la tierra (donde tiene su máximo negativo) hasta
llegar a cero en el infinito.
La energía cinética por el contrario siempre es positiva, aunque si lanzamos un cuerpo
hacia arriba ira disminuyendo hasta llegar a cero.
La energía mecánica total, que es la suma de la cinética y de la potencial, podrá por lo
tanto ser negativa, cero o positiva.
Energía mecánica negativa: Si la energía mecánica es negativa decimos que el cuerpo está
ligado a la gravedad terrestre y que por tanto no puede escapar de su campo. Pueden ocurrir:
A) Si la velocidad es menor que la de escape “y tiene la dirección del peso” sería como tirar
una piedra verticalmente hacia arriba: subirá hasta una determinada altura (más o menos
grande dependiendo del valor de la velocidad inicial) y volverá a caer al suelo.
Ep Superf .Tierra + Ec quelehemos = Ec arriba + Ep arriba < 0
comunicado
Como ∆Ec+∆Ep=0 → mientras sube, la disminución de ∆Ec conlleva un aumento de la
∆Ep y al contrario mientras baja.
B) Si la velocidad con que lo lancemos “tiene componente vertical y horizontal” el cuerpo
subirá hasta la altura h (la componente vertical de la velocidad es quien le hace subir) y allí
pueden pasar tres cosas:
b1. Que la componente tangencial de la velocidad sea igual a la que debe tener para orbitar
v
= GM / r . En ese caso, una vez arriba, describirá
a esa altura a la que ha llegado orbital
una órbita circular alrededor de la tierra y su energía como hemos deducido valdrá:
1 M⋅m
E=− G
2
r
b2. Que la componente tangencial de la velocidad < vorbital. Entonces volvería a la
superficie terrestre, como ocurre cuando lanzamos una piedra o un proyectil a poca
velocidad.
b3. Que la componente tangencial de la velocidad > vorbital (pero más pequeña que la de
escape) entonces el cuerpo seguirá ligado al campo gravitatorio, pero describirá una órbita
elíptica en lugar de circular.
Energía mecánica cero : Si la energía mecánica es cero (Ec+Ep=0), entonces el satélite
tendrá la energía mínima para escapar del campo, y lo haría siguiendo una trayectoria
parabólica. A la velocidad necesaria se le llama velocidad de escape: v escape = 2GM / r
Energía mecánica positiva: Es decir, si le comunicamos una velocidad tal que Ec>Ep
entonces, por supuesto escapará del campo gravitatorio, pero lo haría siguiendo una
trayectoria hiperbólica. Además como puede suponerse llegaría al infinito con una
velocidad>0.
E6B.S2008
a) Explique qué se entiende por velocidad de escape de la Tierra y deduzca razonadamente su
expresión.
b) Suponiendo que la velocidad de lanzamiento de un cohete es inferior a la de escape,
explique las características del movimiento del cohete y realice un balance de energías.
EJEMPLO:
a) Se lanza hacia arriba un objeto desde la superficie terrestre. Calcula la velocidad inicial que
hemos de comunicarle para que llegue a una distancia r del centro de la tierra. Particularice la
expresión de la velocidad inicial para puntos próximos a la superficie terrestre.
b) Comente los cambios energéticos que tienen lugar durante el ascenso del objeto
considerando despreciable el rozamiento.
c) Calcule la velocidad orbital para que gire en una órbita r
d) Se lanza hacia arriba un objeto desde la superficie terrestre. Calcula la velocidad inicial que
hemos de comunicarle para que llegue a una distancia r del centro de la tierra y orbite.
e) Calcular la velocidad de escape del objeto si lo lanzamos desde la superficie de la tierra. ¿ y si
lo lanzáramos desde la órbita de radio r?
DATOS: G, MT, RT, m = masa del objeto
a) Cuando a un cuerpo le comunicamos (por algún procedimiento) una energía cinética estamos
aumentando su energía mecánica y puesto que la fuerza gravitatoria es conservativa podemos
aplicar el principio de conservación de la energía mecánica. Teniendo en cuenta que si se lanza
verticalmente hacia arriba irá subiendo hasta pararse, poner que:
Ec tierra + Ep tierra = Ec P + Ep P

M ⋅m 1
M ⋅m
1

 = mv 2P +  − G T
mv 02 +  − G T

2
RT  2
r 


de donde:
 1 1
 r − RT
v 0 = 2GM T 
−  = 2GM T 
 RT ⋅r
 RT r 

 h 
 = 2GM T 

R
⋅
r

 T 
Particularización para puntos próximos a la superficie terrestre: Teniendo en cuenta que en tal
caso las distancias entre las masas RT y r son prácticamente iguales, y que la gravedad es g =
GMT/R2 podemos poner:
 h
v 0 = 2GM T  2
 RT

 = 2 g h

En realidad este ejercicio es igual al que hemos resuelto en cursos anteriores (aunque utilizando la
expresión de Ep válida para puntos próximos): “Calcular la altura que alcanza un cuerpo cuando se le
comunica verticalmente y hacia arriba una inicial vo”. En tal caso lo que hacíamos era aplicar,
exactamente igual, la conservación de la energía mecánica, pero asignábamos nivel cero de Ep en la
superficie de la tierra y la expresión mgh para la Ep a una altura h: (sería igual si asignamos EpA=mghA
y a EpB=mghB ya que en tal caso mg(hB– hA) =mgh )
Ec tierra + Ep tierra = Ec P + Ep P
1
mv 02 + m g h A = 0 + m g h B
2
→
v0 = 2g h
b) De acuerdo al principio de conservación de la energía mecánica, ∆Ec + ∆Ep = 0 , como el
incremento de energía cinética es negativo (puesto que al subir va disminuyendo su velocidad),
la energía potencial debe incrementarse en el mismo valor pero positivamente.
c ) Teniendo en cuenta que para un observador no inercial que se mueva con la masa m la fuerza
resultante sobre ella es nula:
M ⋅m
GM T
v2
Fgrav = Fc → G T 2 = m
→ v orbital =
r
r
r
d) d1.Este caso es parecido al apartado a) con una diferencia: que una vez que llegue a la
distancia r no puede tener velocidad nula, sino precisamente una velocidad igual a la
velocidad orbital y además esa velocidad debe ser tangencial (ya que si tuviese componente
vertical seguiría subiendo). (En realidad no se hace así, sino que primero se sube el satélite
hasta la altura a que debe orbitar y una vez allí se le comunica horizontalmente una velocidad
igual a la orbital.)
Ec tierra + Ep tierra = Ec P + Ep P

M ⋅m 1
M ⋅m
1

 = mv 2P +  − G T
mv 02 +  − G T

2
RT  2
r 


sustituyendo vp por la velocidad orbital:
2

M ⋅ m  1  GM T  
M ⋅m
1
 + − G T
 = m
mv 02 +  − G T



2
RT  2 
r  
r 

de donde
 2r − R T 

v 0 = GM T 
R
r
T


d2. podríamos haber hecho otro razonamiento (aunque en el fondo es exactamente lo mismo). Se
trataría de calcular la diferencia de energía mecánica que tiene la masa m cuando está en la
órbita r y cuando está parada sobre la superficie de la tierra. Esa diferencia de energía es la que
hemos de comunicarle en forma de energía cinética:
E A = Ec A + Ep A = −G
M⋅m
RT
2
1  GM  
M⋅m
M⋅m
 + − G
E B = Ec B + Ep B = m
 = −G

2 
r  
r 
2r
La diferencia de energía de cuando está orbitando con radio r y cuando estaba en reposo en la
superficie de la tierra es EB–EA=WF.No.Conserv =GMm(2r–R/2Rr)
Teniendo en cuenta que ese trabajo que le comunicamos lo debe adquirir en forma de energía
cinética, tenemos que:
 2r − R T
GMm
 2R T r
 1
 = mv 02
 2
→
 2r − R T
v 0 = GM T 
 RT r



En realidad hay una diferencia entre ambos razonamientos. En el primer caso se parte de que el
cuerpo está sobre la superficie de la tierra, pero ya se le ha comunicado la energía suficiente y por
eso ahora ya todas las fuerzas son conservativas, entonces: ∆Ec + ∆Ep = 0
En el segundo caso se parte de un momento anterior, es decir cuando el cuerpo aun está en reposo
sobre la tierra, y por tanto para que comience a subir necesita que se le comunique una energía,
entonces: ∆Ec + ∆Ep = WA→B
F. NoConservat
d3. Para aclarar los conceptos y enlazar con lo que
aprendimos en los tiros de proyectiles, fíjate que la velocidad
inicial del cuerpo debe formar un cierto ángulo, teniendo dos
componentes:
La componente X de la velocidad inicial debe coincidir con
la velocidad orbital. (ya que durante todo el movimiento es
la misma y por tanto debe ser igual a la que tiene en el punto
más alto)
GM T
r
La componente Y de la velocidad inicial, que tampoco depende del tiempo, es igual a la que
requiere para elevarse hasta una distancia r del centro de la tierra y ya hemos calculado antes.
v 0 x = v orbital =
 r − RT 

v 0 y = 2GM T 
 RT ⋅r 
El módulo de la velocidad inicial será, por tanto:
2
2
v = v 0x
+ v 0y
=
 r − RT
GM T
+ 2GM T 
r
 RT ⋅ r

 2r − R T
 = GM T 

 RT r



No confundas la componente Y de la velocidad inicial con la componente Y del vector velocidad total. Esta sí que depende del
tiempo, ya que este es suma de la velocidad inicial y de la debida a la gravedad sería:
r
v=
 r − RT
GM T r 
i +  2 GM T 
 R ⋅r

r
 T

r

 −g t j




donde g = G
M
r2
La componente Y de la velocidad inicial depende del tiempo, ya que es la suma de la componente Y de la velocidad inicial (que
es constante e igual a la que requiere para elevarse hasta una distancia r del centro de la tierra) y de la debida a la gravedad (que
depende del tiempo).
e) La velocidad de escape es aquella que permite que el cuerpo escape de la atracción terrestre
y ello requiere que su energía total sea positiva o nula como mínimo.
Si queremos que el cuerpo escape completamente debemos comunicarle una energía cinética
de manera que no se detenga hasta llegar al infinito, donde su energía mecánica sería cero
porque llega con velocidad cero y porque allí su Ep=0, ya que es inversa a la distancia. Por
tanto, como la energía mecánica en el lanzamiento debe ser igual a la que tiene en el infinito:
Ec tierra + Ep tierra = Ec ∞ + Ep ∞
E=
1
M⋅m 1
M⋅m


2
2
mv escape
+ − G
 = mv ∞ +  − G

∞ 
2
R  2


de donde:
v escape =
2GM
R
Si el cuerpo estuviera a una altura h la velocidad de escape, sería v escape =
2 GM
r
donde r=R+h
Como puedes ver comparando la velocidad orbital y la velocidad de escape: v escape = 2 ⋅ v orbital
Ejemplo:
¿Con qué velocidad habría que lanzar desde la superficie de la tierra una nave para que llegue
a la luna?
Datos: MT=5,98.1024Kg
ML=7,35.1022Kg dT−L=3,84.108m
Esto es casi igual si que nos pidieran
la velocidad con que hay que lanzar
una piedra para que llegue al tejado.
La pequeña diferencia es que, en
este caso, solo tenemos que llevar el
cuerpo hasta una distancia x donde
el campo gravitatorio y el lunar se
igualan y luego ya será la luna la
que tire del cuerpo y lo lleve hasta
su superficie.
El punto Po donde la gravedad terrestre y lunar se igualan, es decir gT=gL :
G
MT
ML
=G
2
x
(d − x ) 2
→
x=3,45.108m
Y ahora simplemente, aplicamos la conservación de la energía mecánica entre la superficie de
la tierra y ese punto Po donde la gravedad es cero, que es donde hay que llevar al cuerpo.
Ec tierra + Ep tierra = Ec P 0 + Ep P 0
M ⋅m 1
M ⋅m
1


2
mv 2 +  − G T
 = mv Po +  − G T

2
R  2
x 


 1
1
v = 2GM T 
−  = 1,11 ⋅ 10 4 m / s
 RT x 
La intensidad de campo puede ser nula en el infinito o, como hemos visto en este caso, en un
punto entre la tierra y la luna donde la gravedad terrestre se compense con la gravedad lunar.
No obstante, habrás visto la ingravidez aparente de los astronautas en un satélite en órbita. Se
explica sencillamente porque la aceleración del satélite es igual a la aceleración de la gravedad.
v2
v2
Para un observador inercial g ≡ a normal =
y para un observador no inercial g = a centrífuga =
r
r
Sería exactamente igual que si vamos en un ascensor y se rompe la cuerda. La aceleración con
que nos moveríamos sería igual a la de la gravedad, con lo que, respecto de la cabina del
ascensor, tendríamos aceleración cero y la sensación de ingravidez. Si en tal situación
soltamos un objeto nos daría la impresión de que no cae porque siempre guardaría la misma
posición respecto a nosotros, sin embargo respecto de un SRI, realmente ambos estamos
cayendo con una aceleración igual a la de la gravedad.
AMPLIACIÓN
CIRCULACIÓN DE UN VECTOR A LO LARGO DE UN CAMINO C
El concepto de circulación se introdujo primero en hidrodinámica para saber si un fluido circulaba, es
decir si hay un movimiento neto del mismo a través de un camino o conducción.
De la misma forma se puede aplicar al vector Intensidad de campo, aunque en este caso
realmente no hay nada que circule. Imagina un camino cualquiera, abierto o cerrado.
r
r
Tomemos un elemento de camino d r entonces la circulación del vector I a lo largo del
mismo se define como el producto escalar de la intensidad de campo por el vector
desplazamiento:
r r
dC = I • d r
dC = Circulación a lo largo del elemento de camino dr
r
I = Intensidad de campo
r
d r = vector desplazamiento que ya conocemos (vector tangente al camino):
r
r
r
r
d r = dx i + dy j + dzk
α = ángulo que forman la Intensidad de campo y el vector desplazamiento
r
Si dividimos el camino a seguir en elementos d r y evaluamos para cada uno el diferencial de
r
circulación y los sumamos todos, tendremos la circulación total del vector I entre los puntos
A y B a lo largo del camino c. Esto se expresa con la integral de línea siguiente:
Br
r B
C A→B,c = ∫ I • d r = ∫ I ⋅ cos α ⋅ dr
A ,c
A ,c
Se lee: la circulación entre los puntos A y B a lo largo del camino c
Si la circulación fuese a lo largo de un camino cerrado, es decir desde el punto A al B y luego
desde el B al A, tendríamos:
C=
B
A
A ,c1
B,c 2
r r
∫ I • dr +
r
r
r
r
∫ I • dr = ∫ I • dr
La integral con el circulito indica que el camino es cerrado.
El concepto de circulación que se ha definido es aplicable a
cualquier vector:
• La circulación del vector fuerza entre los puntos A y B a lo largo de un camino c no es
más que el trabajo realizado por la fuerza para llevar al cuerpo desde el punto A al B
por ese camino. (Ya recordarás cuando definimos el trabajo, que dijimos que en
general depende del camino seguido. No obstante si la fuerza es conservativa no sería
necesario especificar el camino porque no depende de él.)
Br
r
C A→B,c = ∫ F • d r = WA→ B,c
A ,c
• La circulación del vector intensidad de campo entre los puntos A y B es igual a la
menos la diferencia de potencial entre esos puntos. (En este caso nos da igual el
camino seguido porque la diferencia de potencial entre dos puntos solo depende de la
posición de los puntos.)
B
B
r r
r 
Mr
M 
M
C A→B = ∫ g • d r = VA − VB = ∫ − G 2 u r • d r =  − G  −  − G 
rA  
rB 
r

A
A
Ejemplo:
r r
r
Calcular el trabajo realizado por la fuerza F = 3x 2 y i + x j cuando lleve a una partícula desde
la posición A(0,0) hasta la B(1,2) a través de los caminos:
a) de la recta y = 2 x
b) de la parábola y = 2 x 2
Nos dice que calculemos el trabajo, pero sería exactamente igual si nos hubiesen dicho que
calculemos la circulación del vector fuerza entre esos puntos y por esos caminos, ya que como
sabemos es la misma cosa.
B
WA →B,c1 =
B
r r
∫ F • dr =
A ,c1
∫ (3x
2
r r
r
r
y i + x j ) • (dx i + dy j )
A ,c1
B
WA →B,c1 =
∫ (3x
2
y ⋅ dx + x ⋅ dy)
A ,c1
La integral podemos descomponerla en dos integrales, una donde, como puedes ver, se integra
respecto a x y la otra donde se integra respecto a y.
B
WA →B,c1 =
∫
A ,c1
B
3x 2 y ⋅ dx +
∫
x ⋅ dy
A ,c1
a) Hasta aquí es lo mismo sigas la trayectoria que sigas, porque solamente hemos sustituido F
por su valor y realizado el producto escalar.
fíjate que, por ejemplo, en la primera integral se integra respecto de x, pero la y no es una
constante porque depende de x, así que antes de realizar la integral debemos poner todo en
función de una sola variable y para eso es para lo que necesitamos la ecuación de la
trayectoria, así que como:
camino c1: y = 2 x
•
sustituyendo, la primera integral nos quedaría como:
∫
3x 2 ⋅ 2 x ⋅ dx y los límites de
integración, como integramos respecto de x, serían xA y xB, es decir entre 0 y 1
•
en la segunda integral debemos hacer lo mismo, poner todo en función de una sola
variable. Así que, si despejamos la x y sustituimos, nos quedaría: ∫ y / 2 ⋅ dy pero
también si derivamos la ecuación de la trayectoria tendremos que dy = 2dx , así que
también podríamos optar por poner la segunda integral de la forma:
∫ x ⋅2dx . Da igual
tomar una u otra aunque claro, según optemos, los límites de integración serían desde
yA a yB o desde xA a xB .
WA→B,c1 =
x =1
∫
3x 2 2x ⋅ dx +
x =0
∫ x ⋅ 2dx
x =0
1
WA→B,c1
x =1
[ ]
 6x 4 
2
=
 + x
 4 0
1
0
= 2,50Julios
b) El trabajo para llevar la partícula a lo largo del camino c2 se hace exactamente igual, con la
única diferencia de que ahora la relación entre las variables x e y es distinta, porque viene
dada por la ecuación del camino:
camino c2:
•
•
y = 2x 2
Sustituyendo la ecuación de la trayectoria en la primera integral, nos quedaría
2
2
∫ 3x ⋅ 2x ⋅ dx y los límites de integración, como integramos respecto de x, serían
xA y xB, es decir entre 0 y 1
Teniendo en cuenta que si derivamos la ecuación de la nueva trayectoria ( y = x 2 )
obtendremos dy = 4 x ⋅ dx si sustituimos en la segunda integral nos quedará
∫ x ⋅ 4x ⋅ dx
y los límites de integración, como también integramos respecto de x,
serían xA y xB, es decir entre 0 y 1
WA →B,c 2 =
x =1
∫
3x 2 2x 2 ⋅ dx +
x =0
x =1
∫ x ⋅ 4x ⋅ dx
x =0
1
1
 6x5   4x 
WA→B,c 2 = 
 = 2,53Julios
 +
 5 0  3 0
3
Como puede verse, en general, el trabajo depende de la trayectoria seguida. Por el contrario, si
solo dependiera de la posición de los puntos A y B diríamos que la fuerza es conservativa.
FLUJO A TRAVES DE UNA SUPERFICIE
El concepto de flujo se introdujo en hidrodinámica para expresar el flujo neto de fluido a
través de la superficie. En un campo vectorial se aplica el concepto de flujo de manera
análoga para indicar el número de líneas de fuerza que atraviesan una superficie, aunque está
claro que como las líneas de campo son imaginarias, en realidad a través de la superficie no
fluye nada.
Sea una superficie cualquiera, abierta o cerrada, si tomamos un elemento diferencial de
superficie dS, el flujo (φ) de la Intensidad de campo a través de ella se define como el
producto escalar del vector Intensidad de campo por vector de superficie:
r r
dφ = I • dS
dφ = Flujo a través del elemento dS
r
I = Intensidad de campo que lo atraviesa
r
dS = vector perpendicular a la superficie y de módulo
igual al área del elemento
α = ángulo que forman la Intensidad de campo y la normal a
la superficie
Si dividimos la superficie S en elementos infinitesimales dS y calculamos para cada uno la
diferencial de flujo y las sumamos todas tendremos el flujo total a través de toda la superficie,
lo que se expresa como la integral de superficie:
r r
φ = ∫ I • dS
S
No tienes que preocuparte por la aparición de una integral de superficie, porque en todos los
casos que se van a plantear se resolverá sin tener que recurrir a cálculos complejos. Por
ejemplo:
r
A) Si el campo es constante y perpendicular a la superficie, dS , es decir que I=cte y α=0º nos
quedaría que:
r r
φ = ∫ I • dS = ∫ I ⋅ dS ⋅ cos 0º = I ∫ dS = I ⋅ S
S
S
S
B) Si el campo es constante y paralelo a la superficie, es decir α=90º , entonces, como el
producto escalar es nulo:
φ=0
C) Si el campo es constante y forma un ángulo α con la perpendicular a la superficie:
φ = I ⋅ S ⋅ cos α
Ejemplo:
r
Un cilindro está en un campo eléctrico uniforme E como se indica en la figura. ¿Cuánto vale
el flujo a través del cilindro?
Vamos a calcular el flujo a través de la pared lateral, luego de la cara anterior y luego de la
posterior. Sumando tendremos el flujo total a través de toda la superficie del cilindro
El flujo φ1 a través de la pared lateral es cero, porque el campo y el vector superficie forman
90º y su coseno es nulo:
φ1 = E ⋅ S ⋅ cos α = E ⋅ S ⋅ cos 90º = 0
El Flujo φ2 a través de la cara anterior es:
φ 2 = E ⋅ S ⋅ cos α = E ⋅ S ⋅ cos 0º = E ⋅ πR 2
siendo R el radio del cilindro
El flujo φ3 a través de la cara de atrás es:
φ 3 = E ⋅ S ⋅ cos α = E ⋅ S ⋅ cos180º = −E ⋅ πR 2
El flujo total se obtiene sumando:
φ = φ1 + φ 2 + φ 3 = 0
Más adelante estudiemos el teorema de Gauss, según éste, el flujo total a través de una
superficie cerrada es nulo si no encierra cargas en su interior (o masas en el caso del campo
gravitatorio).
Ejemplo:
Una espira cuadrada de 4cm de lado se encuentra en un campo magnético de 2Weber/m2.
Calcular el flujo que atraviesa a la espira:
a) Cuando está perpendicular al campo
b) Cuando está paralela al campo
c) Cuando forma un ángulo de 60º con la dirección del campo
d) Cuando gira con una velocidad angular ω
Hemos definido el flujo de forma general como el producto escalar de un vector a través de
r
una superficie, En este caso el vector es la inducción magnética B y la superficie, en realidad
no es tal, puesto que una espira no es más que un hilo conductor que se cierra sobre sí,
pudiendo tener forma circular, cuadrada o cualquier otra.
a)
φ = B ⋅ S ⋅ cos 0º = B ⋅ S = 2 ⋅ 0,04 2 = 3,2 ⋅ 10 −3 Weber
b) Cuando la espira está paralela al campo el flujo es cero, porque en ese caso el vector
superficie y el campo forman 90º y su coseno es nulo
c) Cuando la espira forma un ángulo de 60º con la inducción magnética, fíjate que el ángulo
que ésta forma con el vector superficie sería de 30º (no olvides que el vector superficie es
perpendicular a la superficie)
φ = B ⋅ S ⋅ cos 30º = B ⋅ S = 2 ⋅ 0,04 2 ⋅ cos 30 = 3,8 ⋅ 10 −3 Weber
d) Cuando la espira gire con una velocidad angular ω, el ángulo α será función del tiempo,
estando relacionados ambos, como sabemos por: α = α o + ω ⋅ t
φ = B ⋅ S ⋅ cos α = B ⋅ S ⋅ cos ωt
φ = 3,2 ⋅ 10 −3 cos ωt
Se trata del un flujo variable, porque depende del tiempo como puede verse. Mas adelante
veremos que si un circuito (la espira en este caso) es atravesado por un flujo magnético variable,
en él aparece una fuerza electromotriz inducida (e) que viene dada por:
e=−
dφ
d (B ⋅ S ⋅ cos ωt )
=−
= BSω ⋅ senωt
dt
dt
Precisamente en esto se basa la producción industrial de corriente alterna.
FLUJO DE LA INTENSIDAD DE CAMPO A TRAVES DE UNA SUPERFICIE
CERRADA. TEOREMA DE GAUSS
El teorema de Gauss nos permite calcular el flujo de la Intensidad de campo a través de una
superficie cerrada de forma cualquiera. Supongamos una superficie cerrada de forma esférica,
(para mayor sencillez, aunque el resultado es general) y que en su interior encierra una masa
m. El flujo a través de un elementode superficie sería:
r r
dφ = g • dS
El flujo a través de toda la superficie se obtiene integrando a toda ella:
r r
m
m
m
φ = ∫ g • dS = ∫ − g dS = ∫ − G 2 dS = −G 2 ∫ dS = −G 2 ⋅ 4πr 2 = −4πGm
r
r S
r
S
S
S
resolviendo el producto escalar y
teniendo en cuenta que α=180º
La integral de superficie es la suma de
todas las superficies elementales y por
tanto la superficie de la esfera 4πr2
r r
g • dS = g ⋅ dS ⋅ cos180 = −g dS
En el caso de que dentro de la superficie hubiera varias masas, el flujo total sería la suma del
debido a cada una de ellas, es decir que:
φ = −4πG ∑ m i
Es muy importante tener en cuenta que:
•
•
•
Solamente contribuyen al flujo a través de la superficie cerrada las masas (o cargas en el
caso del eléctrico) que se encuentren en su interior.
De ello se deduce que el flujo a través de una superficie cerrada que no contiene masas (o
cargas) en su interior es nulo. La consecuencia es que la líneas de campo gravitatorio son
abiertas (sumideros para las masas y confluyen en un punto) con lo que entrarían en la
superficie por un lado y saldrían por el otro dando resultante de flujo nula.
El flujo a través de la superficie cerrada es independiente de la posición de las masas en su
interior, ya que su expresión no depende de r.
El flujo del campo gravitatorio a través de una superficie cerrada debido a las masas
que encierra en su interior siempre es negativo.
Ejemplo:
Dentro de una caja de galletas hay dos bolas iguales de masa m y fuera de ella hay otra bola
también de masa m.
a) Cual será el flujo del campo gravitatorio a través de la caja?
b) Como se calcularía el campo en un punto P fuera de la caja?
Como hemos dicho, solamente contribuyen al flujo a través de la superficie cerrada las masas
en su interior y además que el flujo es independiente de la posición de las masas en el interior
de la superficie:
φ = −4 π G ( m + m )
Sin embargo para calcular el campo en un punto sí que
habría que tener en cuenta a todas las masas, estén donde
estén, y además también habrá que tener en cuenta las
posiciones que ocupa cada masa respecto al punto.
Aplicando el principio de superposición, no habría más que
calcular el valor del campo en el punto P debido a cada
masa por separado y sumarlos vectorialmente.
Ejemplo:
Obtener, utilizando el teorema de Gauss, la expresión de la intensidad de campo gravitatorio
creado por una masa m a una distancia r.
Por supuesto ya sabemos la expresión que tiene, pero vamos a obtenerla a partir del teorema
de Gauss. Dibujamos alrededor de la masa una superficie cerrada que va a ser una esfera cuya
distancia a la masa será r. Según la ley de Gauss:
r r
φ = ∫ g • dS
expresión general del flujo
S
φ = −4πGm
Teorema de Gauss
Como:
r
r
• El vector g y el vector dS forman ángulo de 180º
• El módulo de g es constante en toda la superficie, porque al ser la superficie esférica
en todos sus puntos dista igual a la masa m.
m
− g ∫ dS = −4πGm
⇒
− g ⋅ 4π r 2 = −4π G m
⇒
g=G 2
r
S