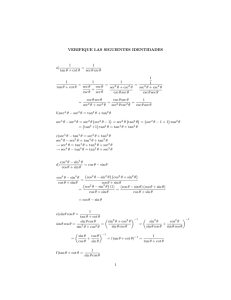
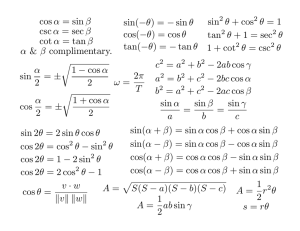sin (A) + cos (A)=1 tan (A) + 1 = sec (A) 1 + cot (A) = csc (A) sin(A + B
Anuncio

sin2 (A) + cos2 (A) = 1 tan2 (A) + 1 = sec2 (A) 1 + cot2 (A) = csc2 (A) sin(A + B) = sin (A) cos (B) + cos (A) sin (B) sin(A − B) = sin (A) cos (B) − cos (A) sin (B) cos(A + B) = cos (A) cos (B) − sin (A) sin (B) cos(A − B) = cos (A) cos (B) + sin (A) sin (B) sin (2A) = 2 sin (A) cos (A) cos (2A) = cos2 (A) − sin2 (A) cos (2A) = 1 − 2 sin2 (A) cos (2A) = 2 cos2 (A) − 1 1 + cos (2A) 1 − cos (2A) cos2 (A) = 2 2 r r 1 − cos (A) A 1 + cos (A) A =± cos =± sin 2 2 2 2 sin2 (A) = sin (A) sin (B) sin (C) = = a b c c2 = a2 + b2 − 2ab cos (C) x= −b ± √ b2 − 4ac 2a an = a + (n − 1)d (a1 + an ) Sn = n 2 an = arn−1 n[2a + (n − 1)d] Sn = 2 1 a(1 − rn ) Sn = 1−r