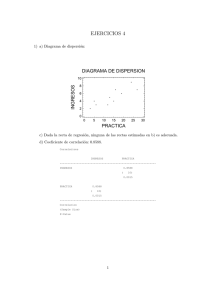
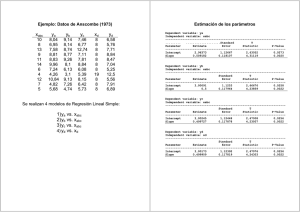
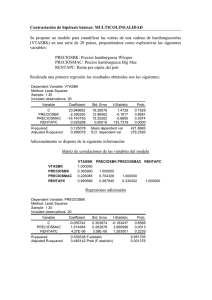
Diapositiva 1 - Posgrado en Ingeniería de Sistemas

Universidad Autónoma de Nuevo León
Facultad de Ingeniería Mecánica y Eléctrica
División de Posgrado en Ingeniería de Sistemas
Diseño factorial aplicado a un modelo
estocástico para apoyo a la toma de
decisiones en una red de logística inversa
Alfredo Esquivel Placencia - AMC
Yulia Anahí Rodríguez Reyes - PROVERICYT
Asesor: Dra. Deniz Özdemir
Tesis: Ing. Leonardo Gabriel Hernández Landa
Introducción
Tradicionalmente, los esfuerzos han sido concentrados en mejorar
las operaciones logísticas tradicionales (forward logistics) pero lo
cierto es que una cadena de suministro completa incluye también a
la logística inversa (Krumwiede and Sheu, 2002).
Plantas
Centro de
Distribución/Inspección
Zona de Clientes
Una de las características principales de la logística inversa es la
incertidumbre en la demanda y la razón de retorno, debido a que
estas pueden variar sobre distintos factores como niveles
económicos, sociales, estacionales, entre otras.
Objetivo



Como parte del proyecto, se desarrollaron varios
diseños factoriales en los cuales se busca conocer
como los factores (precio de adquisición del
competidor y costo unitario de salvamento) afectan a
las variables de respuesta establecidas (costo total,
precio de compra y tiempo en que resolvió la instancia).
Para obtener las variables de respuesta se utilizó el
solver CPLEX, incluido en el software GAMS.
Con el fin de encontrar el valor óptimo del precio de
compra se aplico el método de búsqueda de la sección
dorada.
Modelo
matemático
Descripción del diseño factorial
El experimento del modelo estocástico de logística inversa se refiere a un
diseño factorial, siendo un ejemplo típico de ANOVA:
Con 2 factores:
Factor
Unidades
Precio de adquisición del competidor
$2, $4, $6, $8, $10, $12, $14, $16, $18, $20, $22, $24, $26, $28, $30.
Costo unitario de salvamento
$20, $30, $40, $50, $60, $70, $80, $90, $100.
Donde el factor de precio de adquisición del competidor tiene 15 niveles, y
el factor de costo unitario de salvamento tiene 9 niveles.
Con 3 variables de respuesta:
- Costo total
- Precio de compra
- Tiempo en que resolvió la instancia
Descripción del diseño factorial
 También cuenta con parámetros establecidos:
Factor constante
Unidades
Número de plantas
5
Número de centros de distribución / centros de
inspección
10
Número de zona de clientes
30
Costo fijo de abrir un centro de distribución
$5,000.00, $10,000.00
Costo fijo de abrir un centro de inspección
$7,500.00, $15,000.00
Costo fijo de abrir una planta de remanufactura
$10,000.00, $20,000.00
Porcentaje de producto recuperado
70.00%
Es un experimento con factores de niveles fijos, ya que cada tratamiento
se escogió y se fijo en cada factor.
En base a los resultados obtenidos en cada instancia, se realizaron las
siguientes pruebas para comprobar que los factores y sus interacciones
influyen en las tres variables de respuesta.
Análisis de varianza
Modelo (CD $5,000.00, CI $7,500.00 y Planta de Remanufactura $10,000.00)
Costo total
Df
Sum Sq
Mean Sq
F value
Pr(>F)
apcom
1
23075856
23075856
1.5797
0.2110
costosalva
1 9023728185
9023728185
617.7488
< 2.2e-16 ***
apcom:costosalva 1 1256590440
1256590440
86.0240
4.771e-16 ***
Residuals
131 1913574704
14607440
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Precio de compra
Df
Sum Sq
Mean Sq
F value
apcom
1
1380.04
1380.04
107.424
costosalva
1
2800.60
2800.60
218.001
apcom:costosalva
1
228.64
228.64
17.798
Residuals
131
1682.92
12.85
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’
Pr(>F)
< 2.2e-16 ***
< 2.2e-16 ***
4.554e-05 ***
1
Tiempo en que resolvió la instancia
Df
Sum Sq
Mean Sq
F value
apcom
1
17134
17134
2.2495
costosalva
1
11
11
0.0014
apcom:costosalva
1
766
766
0.1005
Residuals
131
997808
7617
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Pr(>F)
0.1361
0.9698
0.7517
Análisis de varianza
Modelo (CD $10,000.00, CI $15,000.00 y Planta de Remanufactura $20,000.00)
Costo total
Df
Sum Sq
apcom
1
3497657674
costosalva
1
2335464069
apcom:costosalva 1
1593863222
Residuals
131 9337027690
--Signif. codes: 0 ‘***’ 0.001 ‘**’
Mean Sq
3497657674
2335464069
1593863222
71275021
F value
49.073
32.767
22.362
Pr(>F)
1.164e-10 ***
6.747e-08 ***
5.753e-06 ***
0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Precio de compra
Df
Sum Sq
apcom
1
1380.04
costosalva
1
2800.60
apcom:costosalva 1
228.64
Residuals
131
1682.92
--Signif. codes: 0 ‘***’ 0.001 ‘**’
Mean Sq
1380.04
2800.60
228.64
12.85
F value
107.424
218.001
17.798
Pr(>F)
< 2.2e-16 ***
< 2.2e-16 ***
4.554e-05 ***
0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Tiempo en que resolvió la instancia
Df
Sum Sq
Mean Sq
F
apcom
1
714
714
costosalva
1
494
494
apcom:costosalva
1
2800
2800
Residuals
131
1349582
10302
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’
value
0.0693
0.0479
0.2718
0.1 ‘ ’ 1
Pr(>F)
0.7928
0.8271
0.6030
Histograma
Prueba Kolmogorov-Smirnov
La prueba de Kolmogorov-Smirnov compara la función de la distribución
acumulada de los datos observados con la de una distribución normal,
midiendo la máxima distancia entre ambas curvas.
Se utilizó el valor-p para comprobar si el conjunto de datos siguen una
distribución normal, ya que no se cuenta con tablas para muestras de
tamaño de 135. Entre más se acerque el valor-p a 1 se dice que los datos
siguen una distribución normal.
Prueba Kolmogorov-Smirnov
Modelo (CD $5,000.00, CI $7,500.00 y Planta de
Remanufactura $10,000.00)
Costo total
Costo total
One-sample Kolmogorov-Smirnov test
data:
res
D = 0.0575,
Modelo (CD $10,000.00, CI $15,000.00 y Planta de
Remanufactura $20,000.00)
p-value = 0.7641
alternative hypothesis: two-sided
Precio de compra
One-sample Kolmogorov-Smirnov test
data: res
D = 0.0887, p-value = 0.2391
alternative hypothesis: two-sided
Tiempo en que resolvió la instancia
One-sample Kolmogorov-Smirnov test
data: res
D = 0.0529, p-value = 0.845
alternative hypothesis: two-sided
Precio de compra
One-sample Kolmogorov-Smirnov test
data: res
D = 0.0887, p-value = 0.2391
alternative hypothesis: two-sided
Tiempo en que resolvió la instancia
One-sample Kolmogorov-Smirnov test
One-sample Kolmogorov-Smirnov test
data: res
D = 0.0915, p-value = 0.2087
alternative hypothesis: two-sided
data: res
D = 0.0898, p-value = 0.2268
alternative hypothesis: two-sided
Gráfica Q-Q normal
Modelo (CD $5,000.00, CI $7,500.00 y Planta de Remanufactura $10,000.00)
Costo total
Precio de compra
Tiempo en que resolvió la instancia
Gráfica Q-Q normal
Modelo (CD $10,000.00, CI $15,000.00 y Planta de Remanufactura $20,000.00)
Costo total
Precio de compra
Tiempo en que resolvió la instancia
Modelo de regresión lineal
Modelo (CD $5,000.00, CI $7,500.00 y Planta de Remanufactura $10,000.00)
Costo total
Coefficients:
Estimate
Std. Error
t value
Pr(>|t|)
(Intercept)
50216.145
1751.225
28.675
< 2e-16 ***
apcom
-772.625
96.305
-8.023
5.11e-13 ***
costosalva
-535.437
26.810
-19.971
< 2e-16 ***
apcom:costosalva
13.675
1.474
9.275
4.77e-16 ***
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3822 on 131 degrees of freedom
Multiple R-squared: 0.8434,
Adjusted R-squared: 0.8398
F-statistic: 235.1 on 3 and 131 DF, p-value: < 2.2e-16
CostoTotalpron = 50216.145 – (772.625*Precio de
adquisición del competidor) – (535.437*Costo de unitario
salvamento) + (13.675*Precio de adquisición del
competidor*Costo de unitario salvamento)
Precio de compra
Coefficients:
(Intercept)
apcom
costosalva
apcom:costosalva
--Signif. codes: 0
Estimate
3.796502
0.020030
0.083074
0.005833
Std. Error
1.642293
0.090314
0.025142
0.001383
t value
2.312
0.222
3.304
4.219
Pr(>|t|)
0.02235 *
0.82483
0.00123 **
4.55e-05 ***
‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.584 on 131 degrees of freedom
Multiple R-squared: 0.7238,
Adjusted R-squared: 0.7174
F-statistic: 114.4 on 3 and 131 DF, p-value: < 2.2e-16
Las variables de respuesta son significativas, pero
no cumple con la premisa de distribución normal
de los residuales.
Tiempo en que resolvió la instancia
Coefficients:
Estimate
Std. Error
t value
Pr(>|t|)
(Intercept)
294.26905
39.98920
7.359
1.82e-11 ***
apcom
0.66327
2.19911
0.302
0.763
costosalva
-0.15975
0.61221
-0.261
0.795
apcom:costosalva 0.01067
0.03367
0.317
0.752
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 87.27 on 131 degrees of freedom
Multiple R-squared: 0.01763,
Adjusted R-squared: -0.004864
F-statistic: 0.7838 on 3 and 131 DF, p-value: 0.505
No es factible realizar un modelo de regresión
lineal ya que ninguno de sus factores, así como
su interacción son significativos.
Modelo de regresión lineal
Modelo (CD $10,000.00, CI $15,000.00 y Planta de Remanufactura $20,000.00)
Costo total
Coefficients:
Estimate
Std. Error
t value
Pr(>|t|)
(Intercept)
92119.320
3868.331
23.814
< 2e-16 ***
Apcom
-1513.101
212.730
-7.113
6.64e-11 ***
costosalva
-407.500
59.221
-6.881
2.21e-10 ***
apcom:costosalva
15.401
3.257
4.729
5.75e-06 ***
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 8442 on 131 degrees of freedom
Multiple R-squared: 0.443,
Adjusted R-squared: 0.4303
F-statistic: 34.73 on 3 and 131 DF, p-value: < 2.2e-16
CostoTotalpron = 92119.32 – (1513.101*Precio de
adquisición del competidor) – (407.50*Costo de unitario
salvamento) + (15.401*Precio de adquisición del
competidor*Costo de unitario salvamento)
Precio de compra
Coefficients:
Estimate
Std. Error
t value
Pr(>|t|)
(Intercept)
3.796502
1.642293
2.312
0.02235 *
apcom
0.020030
0.090314
0.222
0.82483
costosalva
0.083074
0.025142
3.304
0.00123 **
apcom:costosalva 0.005833
0.001383
4.219
4.55e-05 ***
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.584 on 131 degrees of freedom
Multiple R-squared: 0.7238,
Adjusted R-squared: 0.7174
F-statistic: 114.4 on 3 and 131 DF, p-value: < 2.2e-16
Las variables de respuesta son significativas, pero
no cumple con la premisa de distribución normal
de los residuales.
Tiempo en que resolvió la instancia
Coefficients:
Estimate Std. Error
t value
Pr(>|t|)
(Intercept)
336.41873
46.50706
7.234
3.52e-11 ***
apcom
-0.95855
2.55755
-0.375
0.708
Costosalva
-0.40065
0.71199
-0.563
0.575
apcom:costosalva 0.02041
0.03915
0.521
0.603
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 101.5 on 131 degrees of freedom
Multiple R-squared: 0.002961,
Adjusted R-squared: -0.01987
F-statistic: 0.1297 on 3 and 131 DF, p-value: 0.9423
No es factible realizar un modelo de regresión
lineal ya que ninguno de sus factores, así como su
interacción son significativos.
Conclusiones
En base a los resultados obtenidos se puede concluir lo siguiente:
- Costo total
Siendo la única variable de respuesta de la cual se obtuvo un modelo de
regresión lineal, se puede utilizar para inferir resultados de instancias mayores.
- Precio de compra
A pesar de que los factores son significativos con esta variable de respuesta, no se
cumple con la premisa de normalidad. Los datos obtenidos pueden referir a un
modelo de regresión no lineal.
- Tiempo en que resolvió la instancia
Con esta variable de respuesta no es factible realizar un modelo de regresión lineal
ya que ninguno de los factores, así como su interacción son significativos.
Agradecimientos
Dra. Deniz Özdemir

Ing. Leonardo Hernández

Programa de Investigación Científica y Tecnológica
de la UANL

Doctores y estudiantes de PISIS
