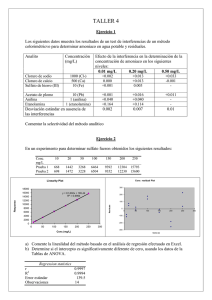
Anscombe

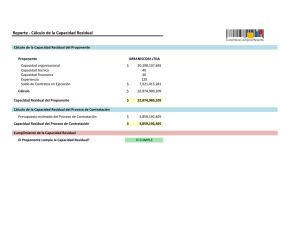
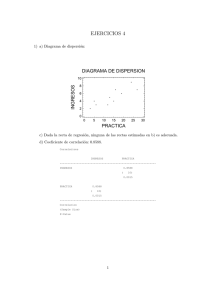
Ejemplo: Datos de Anscombe (1973)
xabc
ya
yb
yc
xd
yd
10
8
13
9
11
14
6
4
12
7
5
8,04
6,95
7,58
8,81
8,83
9,96
7,24
4,26
10,84
4,82
5,68
9,14
8,14
8,74
8,77
9,26
8,1
6,13
3,1
9,13
7,26
4,74
7,46
6,77
12,74
7,11
7,81
8,84
6,08
5,39
8,15
6,42
5,73
8
8
8
8
8
8
8
19
8
8
8
6,58
5,76
7,71
8,84
8,47
7,04
5,25
12,5
5,56
7,91
6,89
Se realizan 4 modelos de Regresión Lineal Simple:
1) ya vs. xabc
2) yb vs. xabc
3) yc vs. xabc
4) yd vs. xd
Estimación de los parámetros
Dependent variable: ya
Independent variable: xabc
---------------------------------------------------------------------.........
....................Standard
T
Parameter
Estimate
Error
Statistic
P-Value
---------------------------------------------------------------------Intercept
2,96373
1,12667
2,63052
0,0273
Slope
0,509182
0,118107
4,31119
0,0020
Dependent variable: yb
Independent variable: xabc
---------------------------------------------------------------------Standard
T
Parameter
Estimate
Error
Statistic
P-Value
---------------------------------------------------------------------Intercept
3,00091
1,1253
2,66676
0,0258
Slope
0,5
0,117964
4,23859
0,0022
Dependent variable: yc
Independent variable: xabc
---------------------------------------------------------------------Standard
T
Parameter
Estimate
Error
Statistic
P-Value
---------------------------------------------------------------------Intercept
3,00245
1,12448
2,67008
0,0256
Slope
0,499727
0,117878
4,23937
0,0022
Dependent variable: yd
Independent variable: xd
---------------------------------------------------------------------Standard
T
Parameter
Estimate
Error
Statistic
P-Value
---------------------------------------------------------------------Intercept
3,00173
1,12392
2,67076
0,0256
Slope
0,499909
0,117819
4,24303
0,0022
Resumen de resultados
Análisis de la varianza
Source
Sum of Squares
Df Mean Square
F-Ratio
P-Value
-----------------------------------------------------------------------Model
28,5193
1
28,5193
18,59
0,0020
Residual
13,8098
9
1,53442
-----------------------------------------------------------------------Total (Corr.)
42,3291
10
Para los 4 modelos ajustados se tiene: y = 3 + 0.5 x
texp(ȕ0)=2.67
texp(ȕ1)=4.24
VE=27.5
VNE=13.8
VT=41.3
sR2=1.5
r=0.82
R2=66.7%
Correlation Coefficient = 0,820824
R-squared = 67,3752 percent
Standard Error of Est. = 1,23872
(excepto errores de redondeo)
Source
Sum of Squares
Df Mean Square
F-Ratio
P-Value
-----------------------------------------------------------------------Model
27,5
1
27,5
17,97
0,0022
Residual
13,7763
9
1,5307
-----------------------------------------------------------------------Total (Corr.)
41,2763
10
Pregunta: ¿Significa esto que las 4 regresiones son
idénticas?
Respuesta: NO
Correlation Coefficient = 0,816237
R-squared = 66,6242 percent
Standard Error of Est. = 1,23721
Source
Sum of Squares
Df Mean Square
F-Ratio
PValue
-----------------------------------------------------------------------Model
27,47
1
27,47
17,97
0,0022
Residual
13,7562
9
1,52847
-----------------------------------------------------------------------Total (Corr.)
41,2262
10
Correlation Coefficient = 0,816287
R-squared = 66,6324 percent
Standard Error of Est. = 1,23631
Source
Sum of Squares
Df Mean Square
F-Ratio
PValue
-----------------------------------------------------------------------Model
27,49
1
27,49
18,00
0,0022
Residual
13,7425
9
1,52694
-----------------------------------------------------------------------Total (Corr.)
41,2325
10
Correlation Coefficient = 0,816521
R-squared = 66,6707 percent
Standard Error of Est. = 1,2357
Reflexión: Entonces… es que nos hemos olvidado de
algo…¿De qué nos hemos olvidado?
De observar los gráficos de dispersión
Diagramas de dispersión
Plot of Fitted Model
Plot of Fitted Model
13,3
12,2
11,3
ya
yc
10,2
9,3
8,2
7,3
6,2
5,3
4
4,2
4
6
8
10
12
6
8
xabc
10
12
14
xabc
14
Hay una observación atípica e influyente que atrae la
recta hacia ella.
Este modelo no parece tener problemas de
especificación
Plot of Fitted Model
Plot of Fitted Model
13,2
11,1
11,2
yb
yd
9,1
7,1
9,2
7,2
5,1
5,2
8
3,1
4
6
8
10
12
xabc
Hay una clara relación no lineal entre x e y.
14
10
12
14
16
18
20
xd
La recta está determinada por un solo punto.
Gráficos de residuos vs. valores ajustados
Studentized residual
Residual Plot
2,7
1,7
0,7
-0,3
-1,3
-2,3
5
6
7
8
9
10
11
10
11
predicted ya
Studentized residual
Residual Plot
2,7
1,7
0,7
-0,3
-1,3
-2,3
5
6
7
8
9
predicted yb
Studentized residual
Residual Plot
1700
1200
700
200
-300
-800
-1300
5
6
7
8
predicted yc
9
10