DERIVADA DE FUNCIONES REALES

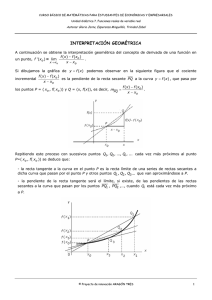
Derivadas
1. Recta tangente a una curva
DERIVADA DE FUNCIONES REALES
Consideremos la curva y = f(x) correspondiente a una función continua
y en ella dos puntos distintos P(x1; y1) y Q(x2; y2). PQ es una recta
secante a la curva con pendiente:
m
y2  y1
x2  x1
Como y2 = f(x2), y1 = f(x1) y si
consideramos x2 – x1 = h
Entonces, x2 = x1 + h
Por lo tanto la ecuación de la recta secante a la curva y = f(x) es:
y  y1 
La noción de derivada ha permitido a lo largo de los siglos hallar
soluciones a problemas como determinar la ecuación de rectas
tangentes a una curva y calcular los valores máximos o mínimos de las
funciones.
f  x1  h   f  x1 
h
.  x  x1 
¿Qué ocurre cuando el punto Q lo consideramos sucesivamente más
cerca del punto fijo P?
La derivada expresa la variación de las funciones entre dos puntos muy
cercanos y se aplica a situaciones físicas como el cálculo de la velocidad
de un móvil, conociendo su ley de movimiento.
Las figuras nos muestran cómo las sucesivas secantes
PQ ; PQ1 ; PQ2 ;............. ; PQn , se acercan cada vez más a la recta
tangente a dicha curva en el punto P.
Profesor: Javier Trigoso
Página 1
Derivadas
Es decir:
La tangente a la curva y = f(x) en el punto P es el límite de las
sucesivas secantes, cuando el punto Q tiende hacia el punto P.
Cuando Q se aproxima a P (Q → P), el número h tiende a cero (h → 0)
Por lo tanto:
La pendiente mT de la recta tangente a la curva correspondiente a la
función y = f(x) en el punto P(x1; y1) es:
mT  lim
h0
f  x1  h   f  x1 
Determina la ecuación de la recta tangente a la curva
correspondiente a cada función real en el punto indicado:
01. f(x) = x2 en el punto (2; 4)
y = 4x – 4
02. f(x) = x2 + 4x + 4 en el punto (-1; 1)
y = 2x + 3
03. f(x) = x2 + 2x + 1 en el punto (1; 4)
h
La ecuación de la recta tangente a dicha curva en el punto P(x 1; y1) es:
y  y1  mT  x  x1 
Ejemplo:
Determina la ecuación de la recta tangente a la curva correspondiente a
la función y  f  x   4x2  3 en el punto (1; 7)
Solución:
Para calcular la pendiente de la recta tangente, usamos la expresión
 4 x  h 2  3  4x2  3
   
f  x1  h   f  x1 
 

, es decir: mT  lim 
mT  lim
h 0
h 0
h
h
Efectuando obtenemos:
h 8x  4h 
8hx  4h2
mT  lim
 lim
 lim 8x  4h   mT  8x
h0
h0
h0
h
h
Como la abscisa del punto (1; 7) es x = 1, tenemos que la pendiente
mT = 8.1 = 8
Luego la ecuación de la recta tangente a la curva en el punto (1; 7) es:
y  7  8  x  1
Profesor: Javier Trigoso
PARA LA CLASE …
04. f(x) 
2
x2
en el punto (3; 2/9)
y = 4x
y = (-4x + 18)/4
2. Derivada de una función real
Como habrás podido observar, en la determinación de la pendiente de la
recta tangente a una curva correspondiente a una función en uno de sus
puntos se ha usado el concepto de límite de una función mediante la
expresión:
f  x0  h   f  x0 
lim
h0
h
A este límite, si existe, se le denomina derivada de una función f(x0)
en x0 y se denota por f’(x0)
En general:
Sea f una función real y sea x0 є R. Decimos que f es derivable en x0 si y
sólo si existe el límite lim
h 0
f  x0  h   f  x0 
h
Página 2
Derivadas
La derivada también se designa por:
y' ;
d f(x)
dx
dy
;
dx
f' x0 
; Dx y ; Dx f(x) ; Dx f
f' x0 
3 x  h 2  9 x  h  4  3 x 2  9x  4 

 0      0 
0
  0

 lim
h0
h
h  6x0  3h  9 
6x0 h  3h2  9h
 lim
 lim
h0
h 0
h
h
f' x0   lim  6x0  3h  9   6x0  9
Ejemplo 1:
h0
2
Calcula la derivada de la función f(x) = x + 3 en el punto x0 = 2
Como la pendiente de la recta tangente es 3 (f’(x0) = 3), entonces:
6x0 – 9 = 3 → x0 = 2
Solución:
Reemplazando x0 = 2 en: f' x0   lim
 2  h 2  3 22  3
   


 lim
h0
h
f 2  h   f 2 
h
h 0
efectuando obtenemos:
y0= 3(2)2 – 9(2) + 4 → y0 = -2
h
h 0
es decir: f'2  lim
Reemplazamos x0 = 2 en la función f(x) = 3x2 – 9x + 4 para obtener y0
f  x0  h   f  x0 
Por lo tanto el punto buscado P(x0; y0) es P (2; -2)
Ejemplo 3:
h  4  h
4h  h2
 lim
 lim  4  h 
h 0
h 0
h 0
h
h
f'2   lim
Si f(t)  3t2  6t es la función que define la trayectoria de un móvil,
encuentra la expresión que determina la rapidez instantánea (velocidad)
en el instante t0
f'2    4  0   4
Solución:
Ejemplo 2:
2
Encontremos el punto de la curva asociada a la función f(x) = 3x – 9x +
4 en el que la pendiente de la tangente es 3.
Solución:
Sea P(x0; y0) el punto buscado, calculemos la derivada f’(x0)
f x0  h  f x0
f' x0  lim
h 0
h
 


 
V  t0   f' x0   lim
V  t0 
V  t0 
f  t0  h   f  t0 
h0
h
3 t  h 2  6 x  h  3 t 2  6t 

 0     0 
0
  0

 lim
h 0
h
h  6t0  3h  6 
6t0 h  3h2  6h
 lim
 lim
h 0
h 0
h
h
V  t0   lim  6t0  3h  6   6t0  6
h 0
Profesor: Javier Trigoso
Página 3
Derivadas
La expresión V  t0   6t0  6 puede ser calculada para distintos valores
3. Propiedades sobre las funciones derivadas de funciones
de t0 obteniéndose así cada rapidez deseada
reales:
IMPORTANTE:
Función
Derivada
f x  c
f' x   0
f  x   xn
f' x   nxn 1
f x  x
La rapidez de un móvil, cuya trayectoria está dada por la función
de posición S = f(t), es la derivada de la función, es decir: v(t) =
f’(t), del mismo modo la aceleración será a(t) = f’’(t),
f' x   1
n
n
f  x   c.g  x 
f  x   g  x  .h  x 
05. f(x) = 3x + 1 en x0 = 1
3
06. f(x) = x2 + 1 en x0 = 3
6
07. f(t) = 3t2 – 5t + 1 en t0 = 5s
25
08. f(t) 
1 2
t  4t  1 en t0 = 3s
2
7
correspondiente a la función f(x)  x3  3x2  1 , en los que la pendiente
(-1; -3) y (3; 1)
3
t
. Donde “x”
3
se mide en metros y “t” en segundos. Hallar su velocidad después de
6seg. De iniciado el movimiento.
38
10. Un punto está en movimiento según la ley: x  t   2t 
Profesor: Javier Trigoso
g x
f' x   n.g  x 
h x
.g' x 
f' x   g' x   h' x 
f' x   c.g' x 
f' x   g' x  .h  x   g  x  .h' x 
f' x  
g' x  .h  x   g  x  .h'  x 
h2  x 
f  x   ex
f' x   e x
f  x   ln x
1
x
f' x   ax .ln a
f' x  
f  x   ax ; (a  0)
f  x   loga x
09. Determina las coordenadas de los puntos de la curva
de la recta tangente es 9.
f x 
n 1
n 1
f x  g x  h x
Calcula la derivada de las siguientes funciones reales:
n
n. x
f x  g x
PARA LA CLASE …
1
f' x  
f x  x

f x  g h x
f  x   senx
f  x   cos x
f' x  


1
x.ln a

f' x   g' h  x  .h' x 
f' x   cos x
f' x   senx
f  x   tgx
f' x  
f  x   ctgx
f' x  
1
cos2 x
1
sen2 x
Página 4
Derivadas
Ejemplo 1:
h'(x) 
3
Sean f y g dos funciones reales tales que f(x) = x y g(x) = 4x + 3,
entonces la derivada de la función producto es:

2x2 x2  3
4x6
  h'(x)    x
2
3

2x4
PARA LA CLASE ….
Solución:

La función producto es: h(x)  f(x).g(x)  x3 . 4x  3
Y su derivada es:

 
 
h'(x)  3x .  4x  3   x  .  4 
h'(x)  x3 '.  4x  3  x3 .  4x  3'
2
3
11. Si f(x) 
1
 x  x2 , calcular: f’(-3)
x
-46/9
5
12. Calcular “n” , si f'(n)  , siendo: f(x)  x2  9
4
5
h'(x)  12x3  9x2  4x3
3
2
h'(x)  16x  9x
13. Dada la función: f(x) 
Ejemplo 2:
Sean f y g dos funciones reales tales que f(x) = x2 + 1 y g(x) = 2x3,
entonces la derivada de la función cociente es:
La función producto es: h(x) 
y su derivada es:
x
h'(x) 
f(x) x2  1

g(x)
2x3
11 5  11x
Calcular “a”, si: f'(a) 
1
128
1
14. Calcular f(-1) en la función f(x), que verifica f'(x)  4x  3
f (1) = 10
Solución:
1
,
4
15. Dada la función f(x) que verifica: f''(x)  6x  4; f'(1)  10; f(0)  4
Calcular: f(-1)
2
     
2x 
2x  . 2x    x  1 .  6x 
h'(x) 
2
 1 '. 2x3  x2  1 . 2x3 '
3
3
h'(x) 
Profesor: Javier Trigoso
2
4x6
4x 4  6x 4  6x2
4x6
2
2

2x 4  6x2
4x6
Página 5
Derivadas
4. Aplicación de máximo y mínimo de una función
Si x = 27 → V  4 27
Ejemplo 1:
no nos sirve pues no es posible armar una caja cuyo volumen sea igual a
cero.
Con una cartulina de 54 cm de lado se quiere construir una caja sin
tapa de base cuadrada y volumen máximo. Calcula las dimensiones que
debe tener la caja.
Solución:
Para construir la caja debemos trazar paralelas a los lados a una
distancia “x” de cada borde de la cartulina, recortar los cuadrados de
lado “x” determinados en cada esquina y luego doblar la cartulina por las
líneas marcadas (fig. 1)
3
 
3
 
Si x = 9 → V  4 9
2
 216 27   2916 27   0 , entonces este valor
2
 216  9   2916  9   11664 , “V” toma el valor
máximo, entonces las dimensiones de la caja son: lado de la base:
(54 – 2x) = 54 – 18 = 36 cm, altura: x = 9 cm
Ejemplo 2:
De todos los rectángulos de 25 cm2 de área, ¿cuál es el de menor
perímetro?
Solución:
Si llamamos “x” a la base, “y” a la altura y
“p” al perímetro del rectángulo (ver figura)
• p = 2x + 2y …………………(1)
• Área del rectángulo = 25
25
xy  25  y 
.........(2)
x
De esta manera se construye una caja (fig. 2) de altura “x”, área de la

base iguala a (54 – x)2 y volumen “V”, donde: V  54  2x
2

.x o bien:
V  4x3  216x2  2916x y como “V” es función de “x”, es decir:
V  f(x)  4x3  216x2  2916x , el problema a resolver, consiste en
hallar un máximo de f(x).
Calculemos la derivada de f(x), es decir: f'(x)  12x2  432x  2916
 25 
50
Reemplazando (2) en (1): p  2x  2 
  2x 
x
x


 
y como “p” es función de “x”, es decir p  f x  2x 
derivando f(x) resulta f' x   2 
50
x
50
, que se anula para x = 5
x2
Luego el rectángulo buscado es un cuadrado de 5 cm. Lado.
Factorizando resulta: f'(x)  12  x  27  x  9 
Luego: f'(x)  12  x  27  x  9  0
Profesor: Javier Trigoso

x  27  x  9
Página 6
Derivadas
PARA LA CLASE ….
03. Halla la derivada de la función f(x)  sen2 x
A. 2senx
16. La suma de dos números es 18, encuentra dichos números tales que
la suma de sus cuadrados sea mínima.
B. senx.cosx
C. sen2x
04. Dada la función: f(x)  x2  3 Calcular: P  f
3
3
6
2
17. Si la suma de la base y la altura de un triángulo es igual a 38 m.
¿Qué dimensión debe tener dicho triángulo para que su área sea
máxima?
a)
18. Hallar el área máxima de un rectángulo que tiene su base inferior en
el eje “x” y dos de sus vértices en la curva: y = 6 – 2x2
función y  2x2  5x  1 en el punto P(-3; 2)
19. Hallar el área del mayor rectángulo con lados paralelos a los ejes de
coordenadas, que pueden inscribirse en la región limitada por las
parábolas. 3y= 12 – x2 ; 6y = x2 - 12
20. Un paralelogramo y un triángulo tiene un vértice común y los otros
vértices del paralelogramo están sobre los lados del triángulo dado.
Calcular el área máxima del paralelogramo que se puede inscribir de
esta forma. Base del triángulo = 10; Altura del triángulo = 6.
A. -6
B. -3
02. Dada la función: f(x) 
A. -2
B. -1
b)
c)
 3   f  6 
d) 3 3
e) 2 3
05. Halla la ecuación de la recta tangente a la curva definida por la
A. x – y – 1 = 0
D. 7x + y + 19 = 0
B. x – y + 1 = 0
E. x + y = 0
C. x + y – 1 = 0
06. Halla la ecuación de la recta tangente a la curva definida por la
función y  senx  cos x en el punto P (0; 1)
A. y = x + 1
D. y = 3x + 1
B. y = x - 1
E. y = 4x + 1
C. y = 2x + 1
07. Halla el mínimo valor de la función f(x)  2x2  8x  1
A. -12
B. -10
C. -9
D. -7
E. -5
x
2
1
C. 0
x 1
x 1
C. 0

3
 2  6x  3 , calcular f’(0)
D. 4
E. 6
, calcular f’(4)
D. 1
E. 2
π
09. Dada la función f(x)  ln  sen2x  calcular f' 
8
A. 1
B. 2
C. 4
D.
2
E. 0
10. Indica el área máxima de un rectángulo de lados (3 – 2x) y (x + 1)
A. 25/4 u2
B. 25/2
C. 25/8
D. 5/2
E. 35/4
11. La función desplazamiento de un móvil está dada por
f(t)  3t2  t  1 ¿Cuál es la rapidez en el instante t = 2?
A. 5
Profesor: Javier Trigoso
3
E. 2
08. ¿Cuál es el producto mínimo de dos números cuya diferencia es 4?
A. 5
B. 12
C. 0
D. -3
E. -4
PARA LA CASA ….
01. Dada la función: f(x) 
D. 2sen2x
B. 6
C. 11
D. 18
E. 19
Página 7
Derivadas
12. ¿Cuál es el valor de “p” para que el mínimo de la función
19. Si: f(x)  x 5  x  g(x) 
2
f(x)  x  2x  p sea igual a 10?
A. 8
B. 9
C. 10
D. 1
E. 1/2
13. El desplazamiento de un móvil está dado por la función
3
2
f(t)  2t  5t  t . Encuentra la expresión que define su aceleración
instantánea.
A. 6t2 – 10t + 1
D. 10t – 12
2
B. 6t – 10t
E. 8t - 5
C. 12t – 10
14. Encuentra un número real tal que al restarle su cuadrado, la
diferencia sea máxima.
A. 1
B. 3/4
C. 1/4
D. 1/2
E. 2
15. Determina dos números que sumados den 100, tal que la suma del
cuadrado de uno de ellos con el séxtuplo del otro sea mínima.
A. 5 y 95
B. 3 y 97
C. 6 y 94
D. 8 y 92
E. 4 y 96
16. Se tiene la derivada de una función: f(x)  3x2  2 calcular: f(-1);
si f(0) = 1
A. 0
B. -1
C. 1
D. 2
E. -2
x
1
17. Siendo: f(x) 
¿para que el valor de “a” se cumple f(a) 
;
xa
a2
a  0?
A. 1
B. 3
C. 2
D. 5
E. 4
4
 x3  1 
18. Dada la función f(x)  
 , hallar f´(-1)
 2x3  1 


A. 288
B. -288
C. 298
D. -298
Profesor: Javier Trigoso
A. -15
2
x2
C. 3
B. -2,5
; calcular: R 
f'(1)
g'(2)
D. 25
E. -56
20. Calcula la medida de cada cateto de un triángulo rectángulo de 10
cm de hipotenusa que tenga área máxima.
A. 2 15 y 2 10 cm
B.
D. 3 10 y 10 cm
E. 6 y 8 cm
70 y 30 cm
C. 5 2 y 5 2 cm
21. Dadas las funciones: f(x)  x5  5x4  10x2  6 ;
g(x)  x5  4x3  2x  3 Calcular P 
A. 2
B. 3
C. 4
f''( 1)
g''( 1)
D. 5
E. 8
22. Sea la función: f(x)  ax2  bx  1 ; si f(0) = 3; f(1) = 1
ac
1
1
Además: f    f   . Calcula el valor de: R 
c
b
2
2
A. 0
B. 1/3
C. 4
D. 1/4
23. Dada la función: f(x) 
calcular: “ab”
A. 128
B. -64
ax  b
4x
E. ½
, si su derivada es: f"(x) 
C. 64
D. -128
2x
3/2
4  x
E. 32
24. Encuentra dos números positivos cuya suma sea igual a 20, además,
el cuadrado de uno de ellos por el cubo del otro sea máximo.
A. 6 y 14
B. 7 y 13
C. 5 y 15
D. 4 y 16
E. 8 y 12
E. 188
Página 8
Derivadas
25. Una recta pasa por el punto P (3; 4) y corta a los semiejes positivos
formándose un triángulo, encuentra la ecuación de la recta para que el
área de la región triangular sea mínima.
A. 4x – 3y + 24 = 0
B. 4x – 3y - 24 = 0
C. 4x + 3y - 24 = 0
D. 3x + 4y + 24 = 0
E. 3x + 4y - 24 = 0
26. Sea las funciones: f(x)  senx  g(x)  tanx
Donde: x pertenece en primer cuadrante. Además se tiene que:
 1 
(f(x))(g(x))  2 . Hallar: Q (x) ; si :Q(x)  f(x)2  
 g(x) 


A. 1
B. 2x
C. x + 1
Si se tiene el siguiente triángulo rectángulo:

Senα   (Cosα) 

Nos piden hallar: f  α  
Cosα  Senα
con respecto al
A. 5
B. 7
C. 4
D. 3
E. 6
D. 0
E. 2
5
3
29. Las gráficas adjuntas corresponden a las
1
 g(x)  3x  3
funciones: f(x)  2x2  2x 
2
Determina la máxima longitud vertical “d”.
A. 25/8
B. 15/2
C. 21/8
D. 17/4
E. 1
d
30. Un torpedero está anclado a 9Km del punto más próximo a la orilla.
Se necesita enviar un mensajero al campamento situado en la orilla. La
distancia entre el campamento y el punto más próximo referido es de 15
Km.: teniendo en cuenta que el mensajero recorre a pie 5 Km. /h y en un
bote remando 4 Km. /h. Indicar en que pinto de la orilla debe
desembarcar para llegar al campamento lo más pronto posible.
A. a 3 Km. del campamento
B. a 5 Km. del campamento
C. a 2 Km. del campamento
D. a 8 Km. del campamento
E a 4 Km. del campamento
4
27. Si el propietario de un teatro cobra S/. 10 por cada boleto de
admisión, la asistencia promedio será de 100 personas. Si por S/. 1 de
incremento en el precio del boleto, la asistencia promedio desciende en
dos personas ¿A cuánto debe vender cada entrada para obtener una
ganancia máxima?
A. S/. 10
B. S/. 15
C. S/. 20
D. S/. 30
E. S/. 21
28. Una pieza larga y rectangular de lámina de 30 cm. De ancho la
convirtiese en un canal para agua doblando hacia arriba dos de sus lados
hasta formar ángulos rectos con la base. ¿Cuál debe ser el ancho de las
partes dobladas, si se desea que tenga la mayor capacidad posible?
A. 5cm.
B. 10cm.
C. 8, 25cm.
D. 6cm.
E. 7, 5cm.
Profesor: Javier Trigoso
Página 9