22-04-2004

Lista de ejercicios propuestos (2)
Matemáticas II
1o¯ de Telecomunicaciones
22–4–2004
1. Sean B ⊆ IR3 , abierto y convexo, y f , g: B −→ IR3 funciones de clase 1. Probar que
rot(f ) = rot(g) en B ⇐⇒ ∃ ϕ: B −→ IR tal que ∇ϕ = f − g en B.
Solución:
=⇒c Si rot f = rot g en B, veamos que entonces f − g es un gradiente en B:
La condición necesaria para que una función de clase 1 sea un gradiente, es que las derivadas parciales cruzadas con las
componentes de la función coincidan, o lo que es lo mismo en IR3 , que su rotacional sea la función 0. Como la derivación es
lineal, Di (fj − gj ) = Di fj − Di gj , se tiene que rot(f − g ) = rot f − rot g y, como por hipótesis estas dos coinciden en B, se
tiene que rot(f − g ) = 0 en B. Luego se verifica la condición necesaria.
Pero B es convexo, luego la condición necesaria es también suficiente en B y ∃ ϕ: B −→ IR tal que ∇ϕ = f − g en B.
⇐=c Si ∃ ϕ: B −→ IR tal que ∇ϕ = f − g en B, veamos que entonces rot f = rot g en B:
Si f − g , de clase 1, es un gradiente en B se verifica que rot(f − g ) = 0 en B y, como 0 = rot(f − g ) = rot f − rot g , se tiene
que rot f = rot g en B.
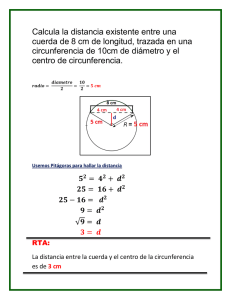
2. El tio Pepe posee un prado de hierba con un palomar cuadrado, de 6 metros de lado, en medio. Si ata la vaca
“Pinta” con una cuerda de 9 metros de larga a una esquina de la pared del palomar ¿cuál es el área de la
superficie de hierba que puede comer la vaca?
Su cuñado Tomás está en la misma situación pero su palomar es circular de 6 metros de diámetro. ¿Cuál es
ahora el área de la superficie de hierba que puede comer su vaca?
Solución: El caso del tı́o Pepe es sencillo y se obtiene fácilmente la solución de manera gráfica.
Si la “Pinta” está atada en un punto P , puede pastar hasta donde alcance la cuerda, es decir,
manteniendo estirada la cuerda se describirı́a un cı́rculo de radio 9. Ahora bien, el palomar
es un obstáculo que la cuerda no puede atravesar, por lo que al llegar la cuerda a la pared
del palomar sólo girará la parte de cuerda que supere la longitud de la pared. Como la pared
tiene 6 metros de larga, sólo 3 metros quedán libres para doblar la esquina Q.
En resumen, la vaca atada en la esquina P puede pastar libremente en los 34 de un cı́rculo
de radio 9, hasta que la cuerda tope con la pared (aparece en color verde en la imagen de
la derecha); a partir de ese momento, la esquina Q asume el papel de punto de amarre de
la parte de cuerda sobrante y, en consecuencia, la vaca sólo puede describir un cuarto del
cı́rculo de radio 3 (hasta que se tope de nuevo con la pared –en dorado en la imagen). Como
esto pasa en cada una de las dos esquinas Q, el área pedida es:
A=
3
Q
6
Q
3
Pr
6
3 2
π32
261π
π9 + 2
=
.
4
4
4
El caso de Tomás es más complejo (el dificil como se apuntaba en la nota al pie). Como en el caso anterior: “la vaca puede pastar
donde alcance la cuerda, describiendo un cı́rculo de radio 9 hasta llegar la cuerda a la pared, cuando se irá enrollando en el palomar
y sólo girará la parte de cuerda que quede libre”.
Pero ahora, al ser el palomar circular, cada punto de la pared actúa como una esquina cambiando el
radio de giro de la cuerda que disminuirá continuamente hasta que toda la cuerda quede enrollada
A
en el palomar.
Si denotamos por B la parte del cı́rculo descrita por la cuerda y por A cada una de las partes
del prado que la vaca puede alcanzar mientras la cuerda se enrolla (podemos girar en los dos
B
sentidos), podemos ver en la figura de la derecha como queda el conjunto (el palomar tiene 3
P
metros radio, luego la longitud de su circunferencia es 6π y por consiguiente, la cuerda no llega a
cubrir media circunferencia, 9 < 3π).
El área pedida es por tanto
A = A(B) + 2A(A) =
1 2
π9 + 2A(A)
2
A
y el problema se reduce a encontrar el área de A.
El conjunto A, está limitado por un segmento, un trozo de una circunferencia de radio 3 y una curva
C
C que desconocemos, pero que debemos averiguar cual es. Para ello, supongamos el centro del palomar
q
situado en el punto (0, 0) y la cuerda sujeta al punto P = (3, 0) y consideremos la situación en un
R
@
momento en que la cuerda se está enrollando al palomar (como en la figura de la izquierda).
@
Si la cuerda se ha enrollado hasta el punto Q, la parte de cuerda que queda libre es 9 − L, donde L es
@ β0 (θ)
@
I
la longitud de cuerda pegada a la pared, es decir, la del arco de la circunferencia del palomar entre el
@
β(θ)
punto de anclaje P y el punto Q (usando el radio de la circunferencia, 3, y el ángulo θ0 = Pd
0Q esta
@qQ
lóngitud es fácil de calcular: L = 3θ0 ).
Manteniendo estirada la cuerda, 9 − L es la longitud del segmento QR y la dirección de este segmento
0
qP
−−→
es tangente a la circunferencia en el punto Q, es decir, podemos describir R como R = Q + QR .
Como el vector tangente se obtiene fácilmente a partir de una parametrización (si (t) es una parametrización, 0 (t) es el vector tangente), parametrizando la circunferencia en polares: (θ) = (3 cos θ, 3 sen θ),
−−→
será Q = (θ0 ) = (3 cos θ0 , 3 sen θ0 ) y QR = λ 0 (θ0 ) = λ(−3 sen θ0 , 3 cos θ0 ), para algún λ.
La parametrización , recorre la circunferencia en sentido positivo, luego el sentido del vector 0 (θ0 ) es el correcto, de Q a R; además
−−→
−−→
0 (θ )
debe ser kQR k = 9 − L, luego QR = (9 − L) 0 0 = 9−L
0 (θ0 ).
3
(θ0 )k
k
Entonces, como L = 3θ0 , se tiene
9 − 3θ0 0
−−→
R = Q + QR = (θ0 ) +
(θ0 ) = (θ0 ) + (3 − θ0 )0 (θ0 ) = (θ0 )
3
: [0, 3] −→ IR2 , donde
y hemos encontrado una parametrización para la curva C,
(θ) = (θ) + (3 − θ)0 (θ) =
¡
3 cos θ − 3(3 − θ) sen θ, 3 sen θ + 3(3 − θ) cos θ
¢
qR
(θ ∈ [0, 3] pues, cuando toda la cuerda está enrollada, abarca un arco de circunferencia de lóngitud 9
que se corresponde con un ángulo θ tal que 9 = rθ = 3θ).
Tenemos ası́ que: la curva C dada por la parametrización , el trozo de la circunferencia del palomar parametrizado por : [0, 3] −→ IR2 (que lo recorre de izquierda a derecha) y el segmento P R
parametrizado por : [0, 1] −→ IR2 donde (t) = (3, 9t), encierran al conjunto A; luego podemos calcular
el área de A como el recinto encerrado por las curvas dadas en paramétricas o usar, como se sugiere la
nota al pie, el Teorema de Green:
Por este teorema, si f es una función de clase 1 tal que D1 f2 − D2 f1 = 1, se tiene que
Z
Z
A(A) =
Z
f d −
1 dxdy =
α(θ)
C
A
6
γ(t)
β(θ)
qP
Z
f d +
f d
A
Por ejemplo, la función
f (x, y) = (− y2 , x2 ) lo cumple, luego
Z
Z
f d −
A(A) =
Z
3
¡
−
0
0
3
f d =
Z
Z
0
3
Z
3
f ((θ)) · (θ) dθ −
f ((θ)) · (θ) dθ +
0
0
0
1
f ( (t)) · 0 (t) dt
0
¢
3 cos θ − 3(3 − θ) sen θ 3 sen θ + 3(3 − θ) cos θ ¢ ¡
,
· − 3 cos θ, −3 sen θ dθ
2
2
−
=
f d +
Z
0
=
Z
Z
3
¡
¢
3 sen θ 3 cos θ ¢ ¡
−
,
· − 3 sen θ, 3 cos θ dθ +
2
2
9
(3 − θ)2 dθ −
2
Z
3
0
9
dθ +
2
En consecuencia,
A=
Z
1
0
Z
1
¡
−
0
9t 3 ¢
,
· (0, 9) dt
2 2
27
81
27
27
81
dt =
−
+
=
.
2
2
2
2
2
π92
81
81(π + 2)
π92
+ 2A(A) =
+2
=
.
2
2
2
2
3. Sean C = {(x, y) : x2 + y 2 = 6}, A el conjunto encerrado por C, la función ϕ: A −→ IR dada por ϕ(x, y) = 4 + xy,
la superficie S1 = graf (ϕ) (superficie dada por la gráfica de ϕ en IR3 ) y f : IR3 −→ IR3 con f (x, y, z) = (−y, −x, 1).
Z
a) Calcular
ϕ.
C
Z
b) Sea C1 la curva borde de la superficie S1 . Calcular
f , indicando el sentido del recorrido.
C1
c) Sean V = {(x, y, z) : (x, y) ∈ A; 0 ≤ z ≤ ϕ(x, y)} y S = fr(V ):
(i) Hallar el área de la superficie S.
(ii) Siendo f el vector densidad de flujo, calcular el flujo saliente a traves de S (indicando el correspondiente
a cada una de las partes que forman S).
Solución: C es la circunferencia centrada en (0,0) y de radio
√
6, en IR2 , luego A es el cı́rculo encerrado por C y
S1 = graf (ϕ) = {(x, y, z) : (x, y) ∈ A; z = ϕ(x, y)} = {(x, y, z) : (x, y) ∈ A; z = 4 + xy}
√
√
a) Si parametrizamos
: [0, 2π] −→ IR2 donde√(t) = ( 6 cos t, 6√
sen t), es de clase
√
√ C mediante
0
0
2
2
1 y (t) = (− 6 sen t, 6 cos t) con lo que k (t)k = 6 sen t + 6 cos t = 6. Entonces
Z
Z
ϕ((t))k (t)k dt =
0
ϕ=
C
Z
2π
0
2π
√
(4+6 cos t sen t) 6 dt =
0
Z
0
2π
√
4 6 dt+
Z
2π
√
√
3 6 sen(2t) dt = 8 6π.
recorrido).
ϕ(x,
q y)
0
b) S1 = {(x, y, z) : (x, y) ∈ A; z = 4+xy}, luego (x, y) = (x, y, 4+xy) con (x, y) ∈ A la parametriza,
S1 = (A), y como C es el borde de A, C1 = (C) es el borde de S1 . Es una curva cerrada,
luego veamos si f (x, y, z) = (−y, −x, 1) es un gradiente:
Para todo (x, y, z) ∈ IR3 , rot f (x, y, z) = (0 − 0, 0 − 0, −1 − (−1)) = (0, 0, 0), luego cumple la
condición necesaria en IR3 que, como es un conjuntoR convexo, la convierte en suficiente. Es
f = 0 (y no importa el sentido del
decir, f es un gradiente en IR3 y por consiguiente,
C1
C1 = κ(C)
C
q
(x, y)
c) V = {(x, y, z) : (x, y) ∈ A; 0 ≤ z ≤ ϕ(x, y)} = {(x, y, z) : x2 + y 2 ≤ 6; 0 ≤ z ≤ 4 + xy} luego
V es el interior del cilindro x2 + y 2 = 6 limitado por abajo por el plano z = 0 y por arriba
por la superficie z = 4 + xy (es decir, S1 ).
Y S = fr(V ) está formada por tres trozos de superficie, la “tapa” superior S1 , la tapa inferior
P y la superficie lateral del cilindro H.
(i) Entonces A(S) = A(S1 ) + A(P ) + A(H).
• A(P ) = 6π, pues es el cı́rculo P = {(x, y, z) : x2 + y 2 ≤ 6; z = 0}.
Z
√
• A(H) =
ϕ = 8 6π, pues H es la superficie vertical de altura ϕ(x, y) y base C,
H=
©
ª
C
(x, y, z) : x2 + y 2 = 6; z = ϕ(x, y)
Z
=
©
ª
(x, y, z) : (x, y) ∈ C; z = ϕ(x, y) .
Z
kD1 (x, y) ∧ D2 (x, y)kdxdy =
• A(S1 ) =
k(−y, −x, 1)kdxdy
ZA p
A
y 2 + x2 + 1 dxdy
=
A
Como A
√ es un cı́rculo, cambiando a polares (x, y) = g (r, θ) = (r cos θ, r sen θ), con
r ∈ [0, 6] y θ ∈ [0, 2π], y det(g 0 (r, θ)) = r, se tiene
Z
2π
ÃZ
√
6
=
0
!
√
r r2 + 1 dr
Z
Por tanto, A(S) = A(S1 ) + A(P ) + A(H) =
Z
Z
3
(r 2 +1) 2
3
0
√
7 7−1
2π 3
S1
Z
2π
3
7 2 −1
dθ
3
dθ =
√
7−1
3
= 2π 7
0
0
Z
f · n, donde n es el vector normal exterior a V , indicando el
f ·n+
f ·n+
¸√6
√
+ 6π + 8 6π.
Z
f ·n=
S
µ
dθ =
0
(ii) Tenemos que calcular
2π
P
H
valor de cada una de las tres integrales de la parte derecha de la igualdad. Como f es de clase 1 y S envuelve a V (es su
frontera), el Teorema de la divergencia nos asegura que
Z
Z
Z
f ·n+
f ·n+
P
S1
Z
f ·n=
H
Z
Ahora bien, div f (x, y, z) = 0 + 0 + 0 = 0, por lo que
Z
f ·n+
S1
Z
f ·n=
S
Z
f ·n+
P
div f .
V
f · n = 0 y basta calcular dos de ellas para
H
tener la otra.
Ya tenemos una parametrización para S1 y es fácil parametrizar P , por lo que haremos estas dos:
• S1 = (A), donde (x, y) = (x, y, 4 + xy) y D1 (x, y) ∧ D2 (x, y) = (−y, −x, 1). Como S1 es la tapa superior y la
tercera componente del vector pvf es positiva (va hacia arriba), el vector normal va en la dirección correcta, luego
Z
Z
Z
f ·n=
S1
Z
2π
ÃZ
A
!
√
6
Z
3
=
dθ =
r + r dr
0
0
0
2π
2π
ÃZ
y 2 + x2 + 1 dxdy =
(−y, −x, 1) · (−y, −x, 1) dxdy =
A
Z
!
√
6
r(r2 + 1) dr
0
dθ
0
√
√
³
´
( 6)4
( 6)2
36
6
+
dθ = 2π
+
= 24π
4
2
4
2
• P = {(x, y, z) : x2 + y 2 ≤ 6; z = 0} es un cı́rculo en el plano z = 0, luego (x, y) = (x, y, 0) con (x, y) ∈ A
y D1 (x, y) ∧ D2 (x, y) = (0, 0, 1). Como P es la tapa inferior y el vector pvf va hacia arriba, es el de sentido
contrario al buscado, luego
Z
Z
f ·n=−
Z
Z
H
Z
f ·n−
f ·n=−
En consecuencia,
P
S1
Z
(x, y, 0) · (0, 0, 1) dxdy = −
A
f · n = −24π − 0 = −24π.
P
0 dxdy = 0
A