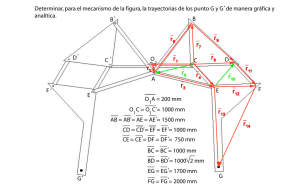
II-1 Revisemos previamente los siguientes temas: Series de

Series de Laurent. Polos y residuos
Revisemos previamente los siguientes temas:
Series de potencias
Una serie de potencias en z = a es una serie infinita de la forma:
∞
∑c
n
(z − a ) n = c 0 + c1 (z − a ) + c 2 (z − a ) 2 + .......... ..... + c n (z − a ) n ...........
n =0
donde z es la variable; c0, c1,...................,cn son los coeficientes y a una constante que recibe
el nombre de centro de la serie.
En particular si a=0, se obtiene una serie de potencias en z :
∞
∑c
n
zn
n −0
La región de convergencia se determina con un círculo de centro a y radio R, tal que en
z − a < R la serie es convergente y si z − a > R es divergente. El círculo z − a = R se llama
círculo de convergencia y su radio recibe el nombre de radio de convergencia.
c
El radio se calcula, por medio de los coeficientes de la serie, L = lim n +1 y según la
n →∞ c
n
1
.
L
Si L = 0 ⇒ R = ∞ la serie converge para todo z.
Si L = ∞ ⇒ R = 0 la serie converge en z = a
fórmula de Cauchy-Hadamard: R =
Ejercicios:
∞
zn
1) ∑
n =1 n
2)
nz n
∑
n
n =1 2
Respuesta: R = 1 y z < 1
∞
Respuesta: R = 2 y z < 2
Series de Taylor
Sea f(z) analítica en todos los puntos interiores a una circunferencia C0 con centro en z0 y
radio r0. En cada punto z interior a C0::
f ′′(z 0 )
f (n)
2
′
f(z) = f(z 0 ) + f (z 0 )(z − z 0 ) +
(z − z 0 ) ................. +
(z − z 0 ) n + R n , esto es la serie
2!
n!
infinita converge a f(z). Rn→ 0 cuando n → ∞.
La convergencia está garantizada si f es analítica en el interior de C0.
El radio máximo es la distancia desde el punto z0 hasta el punto singular de f que esté más
próximo a z0, ya que la función es analítica en todos los puntos interiores a C0.
Ejercicios:
II-1
Series de Laurent. Polos y residuos
1
1) Determinar el radio de convergencia de f (z) =
siendo z0 = j Respuesta: R = 2
1− z
2) Desarrollar f (z ) =
2
en potencias de “z-1”
z−3
SERIES DE LAURENT
z ′ representa cualquier punto sobre una de las dos circunferencias concéntricas C1 ó C2, tal
que
z ′ − z 0 = r1 , z ′ − z 0 = r2 , con centro en z 0 , donde r2 < r1 , entonces:
Si f(z) es analítica sobre C1 y C2 y en toda la región entre estas dos circunferencias,
entonces en cada punto z de esta región, f(z) está representada por una serie convergente
de potencias positivas y negativas de (z - z 0 ) , llamada SERIE DE LAURENT:
bn
n
n =1 (z − z 0 )
∞
∞
f(z) = ∑ a n (z − z 0 ) n + ∑
n=0
an =
(1) donde:
C2
1
f(z ′)
dz ′ (n = 0,1,2,........) (2)
∫
2πj C1 (z ′ − z 0 ) n +1
bn =
C1
1
f(z ′)
dz ′ (n = 1,2,.........) (3)
∫
2πj C 2 (z ′ − z 0 ) − n +1
z0
r2
z’
r1
z’
Los coeficientes de la serie de Laurent se obtienen por métodos prácticos y no por las
fórmulas (2) y (3).
Observaciones:
I) En el caso en que f sea analítica en todo punto sobre C1 e interior a ella, excepto z0, el radio
r2 puede tomarse arbitrariamente pequeño. Así el desarrollo (1) es válido cuando
0 < z − z 0 < r1 . La llamaremos zona cercana.
II) Si f es analítica en todos los puntos interiores y sobre C1, el integrando de la integral sobre
C2 es igual a cero y la serie (1) se reduce a una serie de Taylor. ( − n + 1 ≤ 0 y la función es
analítica en z ′ ) .
∞
III) En particular f (z) = ∑
n =1
bn
(z − z 0 )n
es válido en z − z 0 > r1 . Se demuestra con el punto del
infinito. La llamaremos zona lejana.
II-2
Series de Laurent. Polos y residuos
IV) Puesto que los integrandos de las integrales (2) y (3) son funciones de z ′ en toda la región
anular, cualquier contorno cerrado C alrededor del anillo, puede emplearse como camino de
integración en lugar de C1 y C2 . Entonces la serie de Laurent se puede escribir:
n =∞
f (z) =
∑A
n
(z − z 0 ) n con r2 < z − z 0 < r1 donde :
n = −∞
An =
1
f(z ′)
dz ′ (n = 0, ± 1, ± 2,........)
∫
2ππC1 (z ′ − z 0 ) n +1
La llamaremos zona intermedia.
La serie de Laurent de una función analítica dada f(z) en su anillo de convergencia es
única. Sin embargo f(z) puede tener diferente serie de Laurent en dos anillos del mismo
centro.
Una serie potencial representa una función analítica en todo punto interior a su círculo
de convergencia.
Ejercicios:
1) Encontrar todas las series de Laurent de f (z) =
1
con centro en z 0 =1.
1− z2
n
∞
1
 z − 1
Respuesta: a) f (z) = −
(−1) n 
 válida en 0 < z − 1 < 2
∑
2(z − 1) n =0
 2 
n
∞
1
 2 
b) f (z) = −
.
(−1) n 
 válida en z − 1 > 2
2 ∑
(z − 1) n =0
 z −1
−1
2) Hallar todas las series de Laurent de f (z) =
con centro en z 0 = 0.
(z − 1)(z − 2)
1  z n

Respuesta: a) f (z) = ∑    − z n  válida en z < 1
n =0 
2  2 

∞
1 − 2n
válida en z > 2
n +1
n =0 z
∞
b) f (z) = ∑
∞
 1
zn 
c) f (z) = ∑  n +1 + n +1  valida en 1 < z < 2
2 
n =0  z
Desarrollos en serie más utilizados:
1) Serie binomial:
∞
α
α
 α  α(α − 1)........( α − n + 1)
(1 + z) α = ∑  z n , z < 1; donde   = 1,   =
n!
n =0  n 
0
n
II-3
Series de Laurent. Polos y residuos
Casos particulares:
∞
 − 1
1
1-1)
= ∑  z n , z < 1 ó (1 + z) −1 = 1 − z + z 2 − z 3 + ..............
1 + z n =0  n 
∞
 − 1
1
1-2)
= ∑  (−z) n , z < 1 ó (1 + (−z)) −1 = 1 + z + z 2 + z 3 + ..............
1 − z n =0  n 
1-3) (1 + z) − m = 1 − mz +
∞
2) sen z = ∑ (−1) n +1
n =1
m(m + 1)z 2 m(m + 1)(m + 2)z 3
−
+ ............., z < 1
2!
3!
z 2 n −1
,
(2n − 1)!
z <∞
z 2n
3) cos z = 1 + ∑ (−1)
,
(2n )!
n =1
∞
zn
, z <∞
4) e z = 1 + ∑
n =1 n!
∞
n
z <∞
CEROS DE UNA FUNCIÓN
Supongamos que la f(z) es analítica en el punto z 0 . El punto z 0 se llama cero de la función
f(z) de orden ‘n’ si se cumplen las siguientes condiciones:
f (z 0 ) = 0; f ′(z 0 ) = 0;...............; f ( n −1) (z 0 ) = 0; f (n ) (z 0 ) ≠ 0
Si n = 1 el punto z 0 es un cero simple.
Un punto z 0 es un cero de orden ‘n’ de la f(z), que es analítica en el punto z 0 , si y sólo si,
en cierto entorno de ese punto se verifica la igualdad:
f (z) = (z − z 0 ) φ(z),
n
donde φ(z) es analítica en z 0 y φ(z 0 ) ≠ 0
Ejercicios
Determinar los ceros de las siguientes funciones y encontrar el orden de los mismos.
3
1) f (z) = (z − a )
Respuesta: z 0 = a es un cero de tercer orden
2) f (z) = 1 − e z
3) f (z) =
Respuesta: z 0 = 2kπj es un cero simple
z8
z − sen z
Respuesta: z 0 = 0 es un cero de quinto orden
Los ceros de una función analítica son puntos aislados.
II-4
Series de Laurent. Polos y residuos
SINGULARIDADES DE UNA FUNCIÓN
Singularidad aislada: Si existe cierto entorno de un punto singular z 0 de un función f, en
todo el cual f es analítica, excepto el propio punto, entonces z 0 es un punto singular aislado
de f.
Otra forma de definir es la siguiente: f(z) tiene una singularidad aislada en z = z 0 si es
analítica en un entorno reducido de z 0 .
1
Ejercicio: Encontrar las singularidades aisladas de la función : f (z) =
π
sen
z
Respuesta: Los puntos singulares son infinitos y pertenecen al segmento del eje real de
extremos z = ± 1.
Cuando z 0 es un punto singular aislado de f, existe un número positivo r1 tal que la
función es analítica en cada punto z para el cual 0 < z − z 0 < r1 y en este dominio la
función está representada por la serie de Laurent:
∞
∞
bn
f(z) = ∑ a n (z − z 0 ) n + ∑
n
n=0
n =1 (z − z 0 )
A la última serie se la llama parte principal de f(z) en el entorno de z 0 .
Clasificación:
a) Si la parte principal contiene un número finito de términos, entonces existe un entero ‘m’
tal que los coeficientes b m +1 , b m + 2 ,................. , son todos nulos y el desarrollo de Laurent es:
∞
f(z) = ∑ a n (z − z 0 ) n +
n=0
b1
b2
b m-1
bm
+
+ ........... +
+
2
m -1
(z − z 0 )
(z − z 0 )
(z − z 0 )
(z − z 0 ) m
,
bm ≠ 0
El punto z 0 se llama polo de orden ‘m’. Si m = 1 el polo es simple.
b) Si la parte principal contiene un número infinito de términos, el punto z 0 se llama punto
singular esencial de la función.
c) Si la función no es analítica en z 0 pero puede hacerse analítica utilizando un adecuado
valor de la función; y carece de parte principal, entonces el punto z 0 es un punto singular
evitable.
Polos
I) Si f(z) es analítica y tiene un polo en z = z 0 entonces lim f(z) = ∞
z →z 0
II-5
Series de Laurent. Polos y residuos
Para que un punto z 0 sea un polo de orden ‘m’ de f(z), es necesario y suficiente que f(z)
φ(z)
pueda expresarse de la forma: f(z) =
con φ(z 0 ) ≠ 0 y φ(z) analítica en z 0 (A)
(z − z 0 ) m
Teorema:
z 0 es un polo de orden ‘m’ de f(z) si y sólo si: lim (z − z 0 ) m .f(z) = k , k ≠ 0 , existe, es
z →z 0
finito y no nulo.
Demostración:
Si f(z) tiene un polo de orden ‘m’ en z 0 utilizando (A) se puede escribir:
φ(z) = (z − z 0 ) m .f(z) (0 < z − z 0 < r1 ) donde φ(z) está definida en un entorno reducido de
z0 .
Teniendo en cuenta el desarrollo de Laurent para la existencia de un polo:
∞
(B) ϕ(z) = ∑ a n (z − z 0 ) n + m + b m + b m −1 (z − z 0 ) + ................ + b1 (z − z 0 ) m −1
, bm ≠ 0
n =0
Si z = z 0 entonces ϕ(z 0 ) = b m . Entonces (B) es válida en todo entorno de z 0 y en el propio
punto. Por ser (B) una serie de potencias convergente, la función ϕ( z ) es analítica en z 0 . En
consecuencia se puede escribir:
ϕ(z 0 ) = lim (z − z 0 ) m .f(z) = b m puesto que existe y b m ≠ 0 se deduce que:
z →z 0
lim f (z ) = ∞
z →z 0
II) Si lim f(z) = L entonces z = z 0 es una singularidad evitable.
z →z 0
III) Si lim f(z) no existe entonces z = z 0 es una singularidad esencial de la función.
z→ z 0
Ejercicios:
Analizar los tipos de singularidades en los puntos indicados
1) f (z ) =
sen z
en z 0 = 0
z3
Rta. Polo de segundo orden.
2) f (z ) =
1 − e −z
en z 0 = 0
z
Rta. Singularidad evitable
1
3) f ( z ) = e z en z 0 = 0
1 − cos z
4) f (z ) =
en z 0 = 0
z7
Rta. Singularidad esencial
Rta. Polo de quinto orden
1
5) f (z) = (z − 1).e z −1 en z 0 = 1
Rta. Singularidad esencial
II-6
Series de Laurent. Polos y residuos
RESIDUOS
Definición:
Sea f(z) una función analítica en un contorno cerrado C, simplemente conexo y en todo punto
del interior de C, salvo z 0 . Entonces el residuo de f(z) en z 0 , está definido por:
1
Re s f (z) = b1 =
f (z)dz
según (3) de la página II-2
z =z 0
2πj ∫C
Entonces el residuo de una función f(z) en el punto singular aislado z 0 , es el coeficiente de la
potencia (z − z 0 ) −1 en el desarrollo de Laurent.
Toda función tiene un residuo en cada uno de sus puntos singulares aislados, porque la
serie de Laurent alrededor del punto representa la función en todo un entorno del
punto, excepto en el propio punto.
El valor del residuo puede, sin embargo ser cero.
Ejercicios
Determinar el residuo de cada una de las siguientes funciones en sus respectivas
singularidades.
z 2 − 2z + 3
1) f (z) =
Rta. 3
z−2
1
2) f (z) = e z
3) f (z) =
2
Rta. 0
e −z
(z − 1) 2
Rta. –e-1
FÓRMULAS PARA EL CÁLCULO DE RESIDUOS
A) Para polos simples
A-1) Como lim (z − z 0 ) m .f(z) = b m , si m = 1 entonces b 1 = lim (z − z 0 ) .f(z)
z→ z0
z →z 0
Demostración
Al ser z = z 0 un polo simple, la serie de Laurent correspondiente es de la forma:
∞
f(z) = ∑ a n (z − z 0 ) n +
n =0
b1
con 0 < z − z 0 < r, b1 ≠ 0 . Si multiplicamos ambos
(z − z 0 )
∞
miembros por (z- z 0 ), resulta:
(z- z 0 ). f(z) = ∑ a n (z − z 0 ) n +1 + b1 Aplicando límite:
n =0
II-7
Series de Laurent. Polos y residuos
Res f(z) = b 1 = lim (z − z 0 )f(z)
z =z 0
z→z 0
P( z )
, P(z) y Q(z) analíticas en z 0 y P(z 0 ) ≠ 0 ; Q(z 0 ) = 0 y Q′(z 0 ) ≠ 0 ,
Q( z )
P(z 0 )
entonces el residuo es de la forma: b 1 =
Q ′(z 0 )
Demostración
A-2) Si f (z) =
Si Q(z) es analítica en z = z 0 se puede desarrollar en serie de Taylor, entonces aplicando la
regla A-1) resulta:
P ( z)
Sabemos que
Re s f (z) = lim (z − z 0 ).
z→z0
z =z 0
Q′′(z 0 )(z − z 0 ) 2
Q(z 0 ) + Q′(z 0 )(z − z 0 ) +
+ .............
2!
Q(z 0 ) = 0 y Q′(z 0 ) ≠ 0 , por lo tanto es:
Re s f (z) = lim (z − z 0 ).
z =z 0
z→z0
P( z )


Q′′(z 0 )(z − z 0 )
(z − z 0 ) Q′(z 0 ) +
+ ............... 
2!


P(z 0 )
Res f(z) = b 1 =
z =z 0
Q ′(z 0 )
y pasando al límite :
B) Para polos de orden superior
Sea f(z) una función que tiene un polo de orden ‘m’ entonces b m ≠ 0 y el desarrollo de la
serie de Laurent es de la forma:
bm
b m -1
b1
f(z) =
+
+ ................. +
+ a 0 + a 1 (z − z 0 ) + ..................
m
m -1
(z − z 0 )
(z − z 0 )
(z − z 0 )
Si se multiplica a ambos miembros por (z − z 0 ) m y se construye una función auxiliar analítica
en z 0 que denominamos ϕ(z) se obtiene:
ϕ ( z ) = ( z − z 0 ) m . f ( z ) = bm + bm −1 ( z − z0 ) + ......... + b1 ( z − z 0 ) m −1 + a 0 ( z − z 0 ) m + ............. (I)
Pero (I) es el desarrollo de Taylor de ϕ(z) en z = z 0 donde los coeficientes vienen dados por
ϕ (m −1) (z 0 )
(z − z 0 ) m −1 + .......... (II)
(m − 1)!
(I) y (II) representan el mismo desarrollo, que es único; en consecuencia, comparando
coeficientes, resulta:
ϕ (m−1) (z 0 )
b1 =
; con ϕ(z) = (z − z 0 ) m .f(z)
(m − 1)!
la fórmula: ϕ(z) = ϕ(z 0 ) + ϕ′(z 0 )(z − z 0 ) + ....................... +
II-8
Series de Laurent. Polos y residuos
Ejercicios
Determinar el residuo de cada una de las siguientes funciones en sus respectivas
singularidades.
z 2 − 2z + 3
1) f (z) =
Rta. Re s f (z) = 3
z =2
z−2
1
2) f (z) = e
z2
Rta. Re s f (z) = 0
z =0
−z
3) f (z) =
e
(z − 1) 2
Rta. Re s f (z) = –e-1
4) f (z) =
1
4
z +1
Rta. Re s f (z) =
5) f (z) =
4 − 3z
z2 − z
Rta. Re s f (z) = −4 ,
6) f (z) = z 3 .sen
z =1
9
9
1 − j4π
1 j π
, Re s f (z) = e 4 ,
e
z = z1
z =z 2
4
4
3
3
−
j
π
1 4
1 j4π
, Re s f (z) = e
Re s f (z) = e
z =z3
z=z4
4
4
Re s f (z) = 1
z =0
1
z2
z =1
Rta. Re s f (z) = 0
z =0
TEOREMA DE LOS RESIDUOS
Sea C un contorno cerrado en cuyo interior y sobre el cual una función f es analítica
excepto en un número finito de puntos singulares z 1 , z 2 ,................... ....z m interiores a
C. Si k 1 , k 2 ,......... .............k m representan los residuos f en aquellos puntos se tiene:
∫ f(z)dz = 2πj
C
m
∑ Res f(z)
i =1
z =zi
Demostración:
C1
Encerramos a cada uno de los puntos
singulares zi en un círculo Ci con radio
lo suficientemente pequeño para que
queden separados todos esos ‘m’
círculos y C.
Entonces f(z) es analítica en el dominio
Simplemente conexo limitado por
C1, C2,...........,Cm y sobre la frontera.
z2
z1
C3
Cm
z3
De acuerdo con la integral de Cauchy (una de las
Consecuencias) se concluye que:
II-9
C
C2
zm
Series de Laurent. Polos y residuos
∫ f (z)dz = ∫ f (z) dz + ∫ f (z) dz +........... + ∫ f (z) dz
C
C1
b1 =
Como
C2
Cm
1
f (z)dz
2πj ∫C
∫ f (z) dz = 2πj.k
1
;
C1
⇒
∫ f (z) dz = 2πj.b
1
,
luego :
C
∫ f (z) dz = 2πj.k
2
;
∫ f (z) dz = 2πj.k
................
C2
m
, se
Cm
concluye:
m
∫ f (z) dz = 2πj.(k 1 + k 2 + ........... + k m ) = 2πj.∑ Re s f (z)
i −1
C
z −z j
Ejercicios
Resolver las siguientes integrales aplicando el teorema de los residuos.
1)
3z 3 + 2
∫ (z − 1)(z 2 + 9) dz
C≡ z =2
2)
dz
sh z
C≡ z =4
3)
dz
z (z + 4)
C≡ z =2
Rta. πj
∫
∫
Rta. - 2πj
Rta.
3
π
j
32
EVALUACIÓN DE INTEGRALES REALES MEDIANTE EL CÁLCULO DE
RESIDUOS
Estas integrales surgen en problemas físicos, especialmente en la solución de problemas de
contorno con ecuaciones entre derivadas parciales.
Se presentan distintos tipos de integrales, y analizamos las siguientes:
∞
I) Integrales de la forma:
∫ R(x) dx ;
R(x) es una función racional sin polos reales.
−∞
Para que la integral sea convergente es necesario y suficiente que en la expresión de R(x)
P(x )
como cociente de polinomios R ( x ) =
, los grados verifiquen: gr(P)+1 < gr(Q) ó el gr(Q)
Q( x )
es al menos dos grados mayor que el gr(P).
Para calcular dicha integral, se integra la función compleja R(z) sobre el borde C del
semicírculo z < R, y > 0 y formado por el segmento (-R,R) y dicha semicircunferencia.
II-10
Series de Laurent. Polos y residuos
Para R suficientemente grande, que incluye todos los polos zk situados en el semiplano
superior, tal que:
R
∫ R (z)dz = lim ∫ R (x )dx + lim ∫ R (z)dz
R →∞
C
R →∞
−R
CR
La integral del primer miembro se calcula con el teorema de los
residuos.
La segunda integral del segundo miembro se demuestra
que lim ∫ R (z)dz → 0 , donde CR = R.ejθ ,
R →∞
CR
siendo 0< θ < π.
En consecuencia:
∞
2 πj. ∑ Re s(z k ) =
y k >0
∫ R ( x)dx
−∞
Ejercicio
∞
Calcular
∫x
0
dx
4
+1
Rta.
π 2
4
∞
II) Integrales de la forma:
∫ F(x) cos(mx) dx
∞
ó
−∞
∫ F(x)sen(mx) dx
−∞
En este caso también se usa el camino de las integrales de la forma I) y se trabajan en forma
análoga, previa sustitución de: cos(mz) = ejmz y sen(mz) = ejmz. ‘m’ es una constante
positiva. Téngase en cuenta que Re (ejmz ) = cos (mz) e Im(ejmz) = sen(mz).
Por lo tanto:
R
jmz
jmx
jmz
∫ F(z)e dz = lim ∫ F( x )e dx + lim ∫ F(z)e dz
R →∞
C
2πj. ∑ Re s(z k ) =
y k >0
R →∞
−R
CR
∞
∞
−∞
−∞
∫ F( x ) cos(mx )dx + j ∫ F( x )sen (mx)dx
También aquí se demuestra que lim ∫ F(z)e jmz dz → 0
R →∞
CR
Ejercicio
∞
Calcular:
cos x
dx
2
+1
−∞
∫x
Rta.
π
e
II-11
Series de Laurent. Polos y residuos
2π
∫ F(senθ, cosθ)dθ ,
III) Integrales de la forma:
donde F es un cociente de
0
polinomios en senθ y cosθ.
En este caso el camino es una circunferencia de radio unitario. Consideremos a θ como el
argumento de z sobre la circunferencia unitaria z = ejθθ, entonces:
dz = jejθdθ
⇒
dθ =
ejθ = cos θ +j sen θ
dz
je jθ
y
dz
Además:
jz
e -jθ = cos θ - j sen θ
luego dθ =
e jθ + e − jθ
z + z −1
= cos θ
⇒
cos θ =
2
2
jθ
− jθ
e −e
z − z −1
Restando miembro a miembro se obtiene:
= sen θ
⇒
sen θ =
2j
2j
Con estas sustituciones la integral representará una integral de contorno de una función
racional de z a lo largo de una circunferencia unitaria.
La integral de contorno puede calcularse por el teorema de los residuos si podemos determinar
los ceros del polinomio del denominador.
Sumando miembro a miembro se obtiene:
Ejercicio
2π
Calcular
cos θ
∫ 5 + 4 cos θ dθ
Rta. : −
0
π
3
Demostraciones utilizadas en la resolución de integrales impropias
Teorema de Jordan
Se probará que:
∫ f (z)dz → 0
cuando R → ∞
CR
P( z )
, siendo P(z) y Q(z) polinomios de grado n y m
Q( z )
P (z)
respectivamente, tales que m-n ≥ 2. Consideremos f (z) = n
y tomamos:
Q m ( z)
Este teorema es válido para f (z) =
Pn (z)
Pn (z)
dz ≤ ∫
dz
Q m ( z)
m ( z)
CR
∫Q
CR
Teniendo en cuenta que z = R y
∫ dz = ∫ ds y
z1 + z 2 ≥ z1 − z 2 ⇒
II-12
1
1
≤
z1 + z 2
z1 − z 2
Series de Laurent. Polos y residuos
se puede escribir:
p 0 + p1z + p 2 z 2 + ...... + p n z n
p 0 + p1 z + p 2 z 2 + ........ + p n
Pn (z)
dz ≤ ∫
dz ≤ ∫
∫
CR Q m ( z )
CR q 0 + q1z + q 2 z 2 + ...... + q m z m
CR q 0 − q1 z − q 2 z 2 − ........ − q m
≤
p 0 + p1 R + p 2 R 2 + ........... + p n R n
.πR → 0
q 0 − q 1 R − q 2 R − .............. − q m R m
cuando R → ∞ ((n+1) ≤ m)
Lema de Jordan
Dada una integral de una función f(z) tomada a lo largo de un arco de circunferencia con
centro en el origen, si se verifica que: z.f ( z ) → 0 entonces ∫ f ( z )dz → 0 si R → ∞
R →∞
II-13
CR
zn
zm
ds